职业教育中工程测量课程成绩分析模型研究
2021-03-07刘丽峰牛宗伟
刘丽峰,牛宗伟
(山东理工大学,淄博255049)
1 问题介绍
职业教育中工作至关重要,不仅是就业后工作顺利开展的重要保证,也为就业人员安全提供了有力保障,而学生课程学习作为将来工作的理论基础,也是职业培养计划的基本要求。鉴于以上原因,为分析学生成绩分布的客观规律,以提高教师在课堂上的教学效果,最终达到使学生熟练掌握基本理论知识和实践技能的目的,任课教师如何科学合理地研究成绩模型就特别重要。目前,各高等职业学校的课程成绩分布模型的构建一般以假定班级学生基础知识水平相同或者相差不大的前提来建立学生考试分布模型,这就势必造成忽略不同学生基础知识水平之间的差异,采用相同的尺度评定成绩,进而指导教学,从而在学生学习进度方面不一致,入学学生基础理论较差的学生难以跟上课程进度,从而对学习失去兴趣。为减少任课教师主观认识因素方面的不足对学生课程成绩等级评定的影响,平抑不同入学基础水平方面所给成绩等级的差异,本文提出一种以多因素综合评价为核心的课程等级评定方法。
2 基于多因素分析的考试成绩分析模型
2.1 成绩分析模型综述
目前对成绩分析相关模型的方法有Excel方法[1]、数据仓库的数据挖掘技术[2]、均值、方差、及格率等不同指标方法[3]、矩法[4]、粗糙集算法[5]等,从性别差异[6]、课程分类[7]方面对考试成绩进行分析、利用问卷调研途径建立的定量成绩分布模型[4]、三次Hermite样条和Bspline构造了新的考试成绩标准分布函数[5],张国才则论述了考试成绩可能服从偏态分布[8],胡南和李汶静综合分析教学过程、试题等因素评估教学成果[9],以上研究从不同分析、统计方法和数据角度对成绩的分布进行研究,本文则从影响学生考试成绩的主、客观因素方面对成绩进行分析,进一步建立其分布模型。
本文提出的综合加权平均分模型与一般的评价方法的步骤基本一致,包括:①选择评价指标;②确定分析模型评定标准;③确定指标权重;④选择分析方法;⑤实验分析结果。本模型的不同之处在于,加权平均分分析模型综合考虑学生入学前基础知识水平、社会就业环境影响、学习状况、班级学生的成绩分布等因素。这里的分析指标中优异、良好是基于概率意义上的划分,异于基于成绩的优、良、中、及格等划分,但不及格分级是一致的(<60)。下面针对该分析模型进行具体介绍。
2.2 加权平均分模型构建
(1)确定分析函数指标和标准
单纯的综合评分仅能反映评教的整体成绩,并不能查看学生对课程的关注点、教师教学的薄弱点、学生满意度最高的课程等信息[10-11]。鉴于此,本文考虑了学生对学习的重视程度及对进一步深造的愿望,以及学生间的学习基础及努力程度的差异等因素,选择三个指标构造加权平均分函数,其中自主学习通过考试成绩体现,由于本模型中假设各指标相互独立,因此在不考虑基础知识水平差异的情况下,自主学习的时间与考试成绩(y)成正比。就业形势好坏直接反映在招生的人数上,因此由班级学生考试成绩(S)代表这一指标。针对学生学习努力程度方面主要考虑游戏、娱乐方面因素,这里仅考虑影响学习成绩的游戏、娱乐,受不及格人数影响的平均成绩反应这一指标,该指标仅在模型结果分析时应用。基础知识水平对学生学习难易程度影响较大,由于学生学号(N)跟入学成绩呈反比,即学号末尾数值越小,高考成绩越高,理论基础越扎实。
定义综合加权平均分模型(y=ln(S+2-N*Si)*Ai):以学号、学生考试为自变量的自然对数函数。
(2)确定分析函数指标权重(Si,Ai)
由于分析模型评定指标的权重影响分析模型的精度,因此评定指标权重的选择通过最小二乘方法确定,采用最小二乘法计算学号N学生的综合加权平均模型预测分数与其考试成绩的残差,使残差平方和最小的参数为最优。

3 应用举例
本文采用广东高职高考中专考本科的成绩作为数据源,对综合加权平均模型进行实验分析;广东高职高考中专考本科的考试共有学生148人参与,数据记录完整,因此都用来进行实验,本次考试成绩为百分制。首先采用加权平均分模型对该次考试成绩进行了建模:选择测试分数作为参数S的值,报考序号作为参数N的值;其次根据预测考试成绩的平均成绩与实际考试成绩的平均值最小为原则,应用最小二乘法计算出公式(1)中的权重(Si,Ai)值;最终计算出的综合加权均分模型为:
针对本次实验研究人数较多(148人),学生考试成绩的折线图很难看出该模型计算出的预测成绩之间的变化趋势,见图1(a),因此对预测成绩和考试成绩又做了50、100和150阶导数,见图1(a~d),由图1可以看到预测成绩和考试成绩的导数具有相同的变化频率,但变化幅度不同,从1阶导数到150阶导数变化可以看出,预测成绩和考试成绩的导数折线在0附近震荡,导数阶越高震荡越来越呈现出对称性,且预测成绩和考试成绩的导数折线变化趋势完全一致,就说明了综合加权均分模型能够模拟学生间考试成绩的内在变化规律。
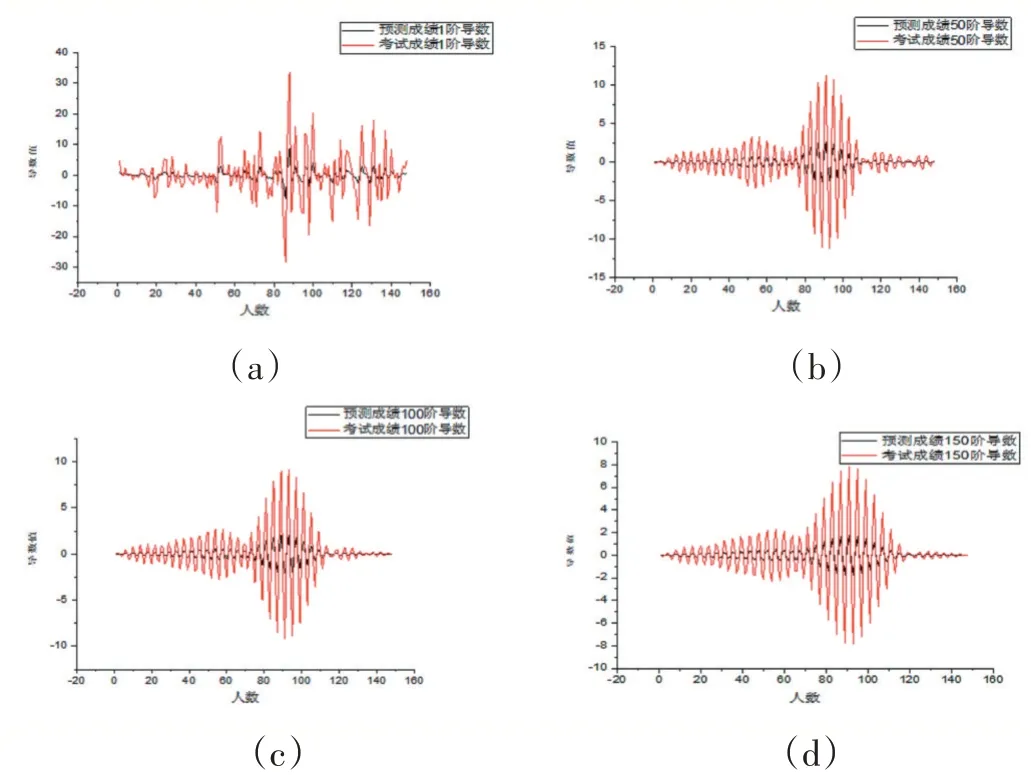
图1 预测成绩与考试成绩的1、50、100和150阶导数(a~d)
由图2可以看出预测成绩和考试成绩都存在2个异常值,其中“×”号表示温和异常值,“-”表示极端的异常值,尤其是考试成绩中87号考试成绩为17.75的极端异常值引起了图1中考试成绩导数值出现了巨大的震荡,根据考试成绩计算出的87号预测成绩也是极端异常值也引起了预测成绩的较大的震荡,但震荡幅度大大减小,说明了综合加权均分模型对极端异常值的出现具有很好的鲁棒性,这对大批量学生数据处理具有重要的意义。
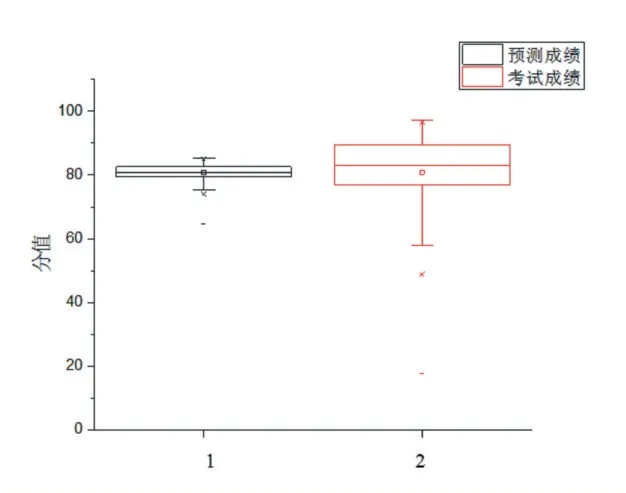
图2 预测成绩和考试成绩箱线图
为研究考试成绩间的整体分布关系,做了预测考试成绩和实际考试成绩的核密度分析图,见图3,由图3可见预测成绩核密度与考试成绩的核密度有相同的变化趋势,但整体预测成绩较考试成绩更聚集,说明综合加权均分模型能够表示出考试成绩的分布状况。
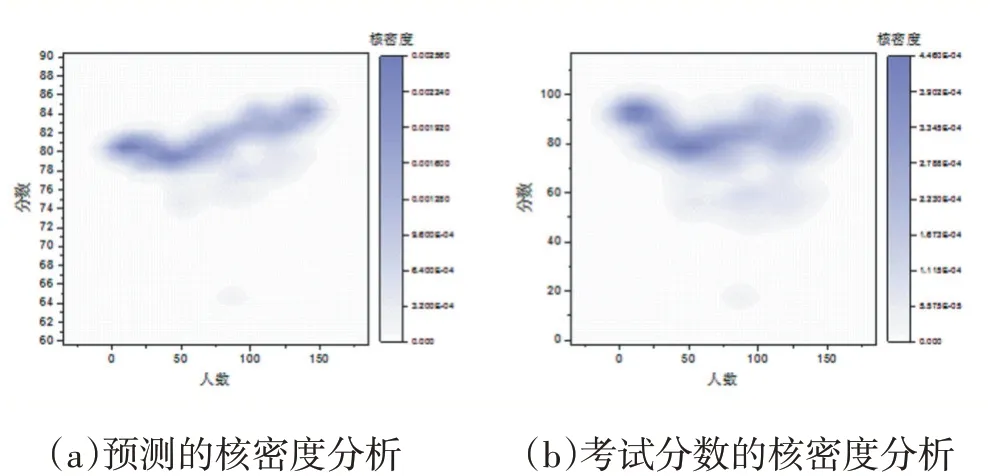
图3
为进一步检验综合加权均分模型计算出的预测分数表达实际考试成绩的质量,本实验还绘制出了预测分数和考试成绩质量控制图(见图4),采用质量控制图研究连续考号中预测成绩与考试成绩的波动情况。在预测成绩与考试成绩2个数据组成的子集,把148个学生组成了148个子集。
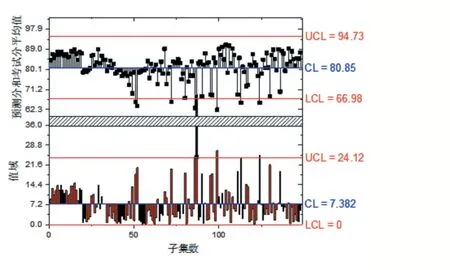
图4 预测分数和考试成绩质量控制图
预测分数和考试成绩质量控制图有两个图层,上面是XBar图,该图由一组带垂线的平均值散点图组成,图中有三条平行线,中间一条为中心线(CL),由全部成绩数据的平均值确定。上下等间距的两条线是上控制线(UCL)和下控制线(LCL)。
控制线与中心线的间距为一个标准差(见图5)。在成绩预测过程中,成绩数据点落入上、下控制线之间,说明考试成绩预测正常。图层2是R(Range)图该层将每个子集值差的值域绘制成柱状图,CL线为各个子集值域的平均值,本层也由上、下控制线。预测分数与考试分数的平均分为80.85,最高分为94.73,最低分为66.98;预测分与考试分差值的平均值为7.38,标准差为4.63,最大值为24.12,最小值为0。
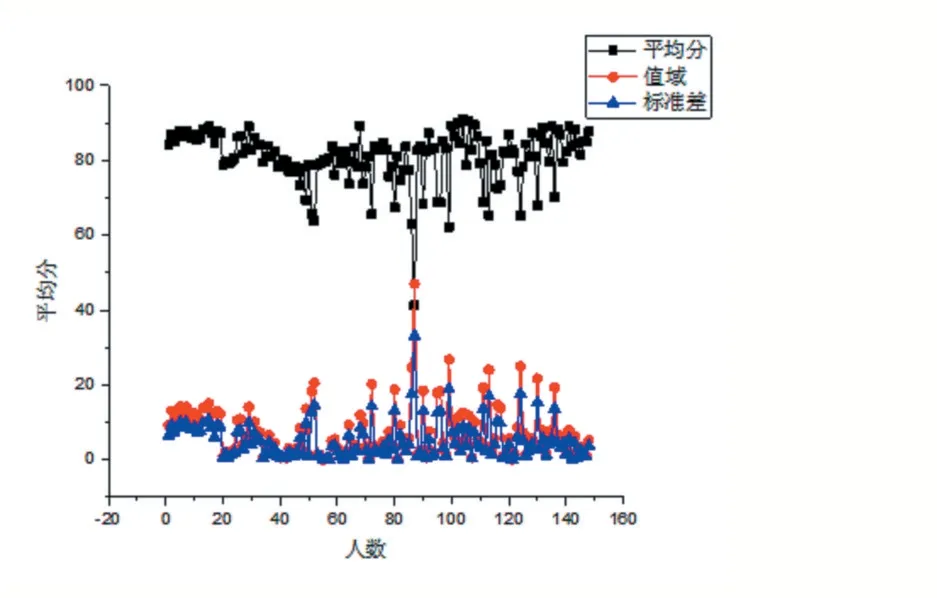
图5 预测分数和考试成绩比较
预测成绩和考试成绩的均值分别为:80.82和80.89,差值仅为-0.07;标准差分别为2.64和12.09,差值为8.73说明预测成绩比考试成绩的值域大大收缩,这也可以从均值的标准差看出,预测成绩和考试成绩的均值标准差分别为0.22和0.99(差值0.51);同时也可以看出预测成绩和考试成绩的中位数差异也不大(-1.41)分别为80.80和83.13。
对预测成绩和考试成绩进行F检验,F为0.3564与1相差甚远,表明组间方差比组内方差小得多,也显示出了预测分数接近考试分数。计算得到的概率P为0.945远大于0.01,故预测成绩对考试成绩的影响不显著。
4 结语
针对当前职业大学学生成绩分析方式的单一性,本文借鉴因子分解的基本概念和方法,根据一般成绩分析模型构建的步骤和原理,分别提出了基于区间法和综合法的加权成绩分析模型,通过实验证明,该方法既适合多个班级单门课程的分析,也适合一个班级多门课程的分析,既适合大学专业课程的分析,也适合中学基础课程的分析,分析方法具有广泛的适用范围;另外,该模型能够有效地分析影响学生考试成绩的因素,对改善教学方法,提高教学质量有重要的意义。经实例应用和结果对比分析,可以认为综合加权平均分模型,可以应用于大中学学生学习成绩的分析中。
