（2+1）维非线性立方Klein-Gordon方程的精确解

王晓利 侯颢天

（1.集宁师范学院数学与统计学院 内蒙古自治区乌兰察布市 012000）（2.乌兰察布市中等职业技术学校 内蒙古自治区乌兰察布市 012000）

1 引言

研究非线性发展方程的精确解能够描述一些物理、生命科学、信息科学、空间科学和环境科学等多领域的非线性现象。但由于非线性发展方程的复杂性，目前还没有较为系统而统一的求解方法。近几年来，人们借助计算机代数和符号计算，构造非线性发展方程的解析解的多种辅助方程法，如反演散射法[1]、Jocobi 椭圆函数展开法[2]、tanh 展开法[3]、G'/G—展开法[4]、展开法[5]、F-展开法[7]等。

（2+1）维非线性立方Klein-Gordon方程[8-10]

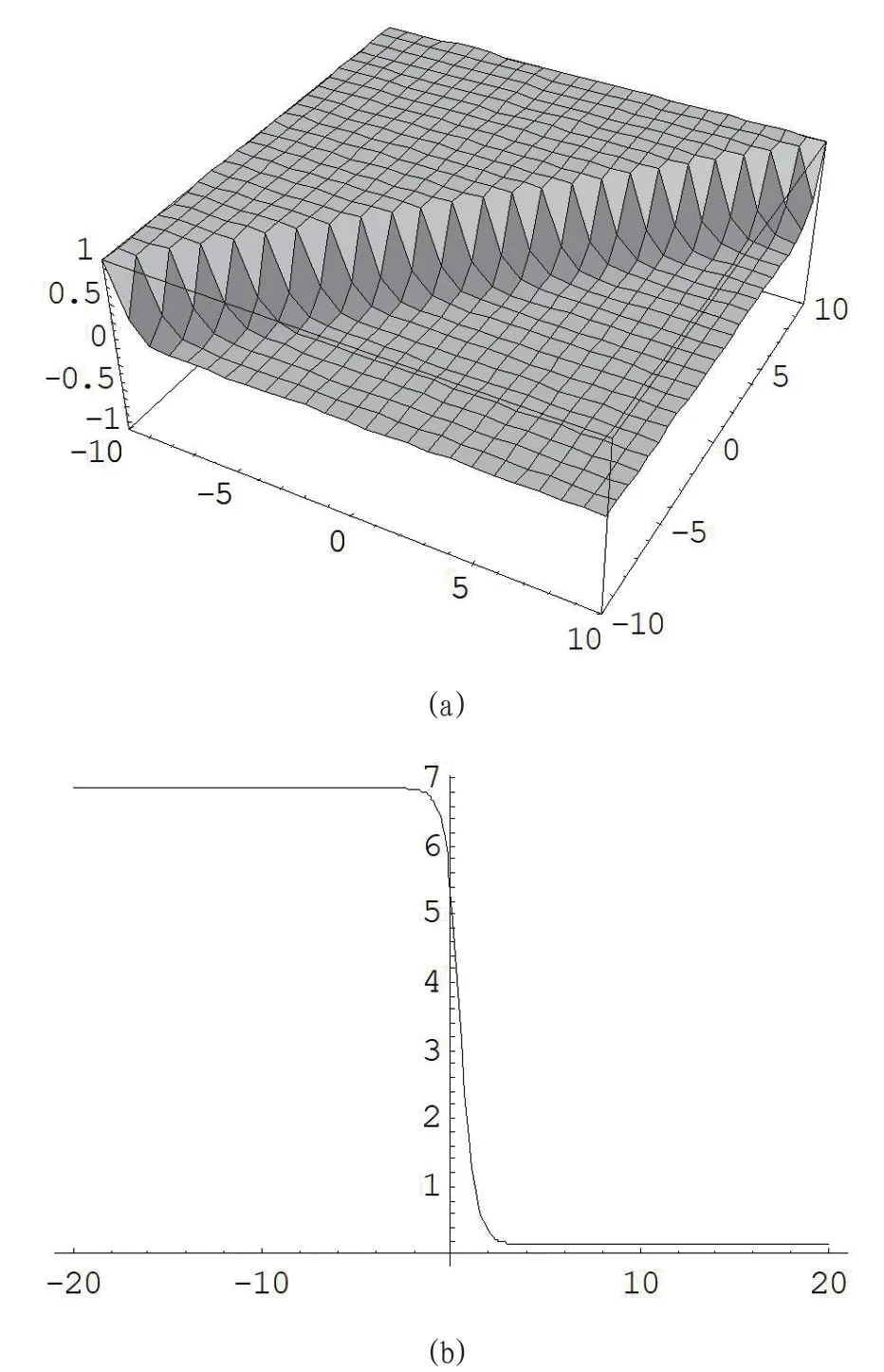
图1：（8）式的解(a) 当λ=4,μ=1，y=0；(b) 当λ=4,μ=1，t=1，y=0。

其中δ，β 为常数。该方程广泛应用于晶体内位错的传播、磁性晶体内Bloch 壁运动、氢键网络中质子的运动、磁通量沿Josephson 传输线传播、统计力学中势能和磁化函数的熵等。文献[8-10]分别利用1/G'-展开法、修正的w/g-展开法及扩展映射法获得非奇异双曲函数解、三角函数周期解及有理解。本文将应用-展开法并借助Maple 软件获得方程（1）的5 组奇异行波新解，包括两组奇异双曲函数解、两组奇异三角函数解和一组奇异指数函数解。

2 （2+1）维非线性立方Klein-Gordon方程的新精确解

假设（1）具有如下形式的行波解：

图2：（12）式的解(a)当λ=1,μ=2，y=0；(b)当λ=1,μ=2，t=1，y=0。

3 结束语

本文应用Exp -展开法获得了（2+1）维非线性立方Klein-Gordon方程5 组新精确解，这些解未出现在其它文献中．之后对于新的精确解的分析将有助于解释与（2+1）维非线性立方Klein-Gordon方程相关的自然现象。