基于高斯混合模型的白光LED封装器件色度预测

俞晟

（江南大学人工智能与计算机学院 江苏省无锡市 214122）

白光LED 作为节能，高效的光源已经逐步替代传统的光源走进人们日常生活当中，白光LED 发光原理是利用LED 芯片发出蓝光，激发涂覆在芯片表面的红黄绿荧光粉，蓝光与受激荧光粉发出的几种光色混合，最终产生白光[1]。评价白光LED 的发光颜色质量的重要指标是发光色度，色度可以通过在CIE（1931）XYZ 坐标系中的位置（横坐标CX,纵坐标CY）来描述。图1 为坐标系中各个相关色温（CCT）对应的麦克亚当椭圆，国际上采用这一系列椭圆规定各色温光源的色度允许波动范围[2]，麦克亚当椭圆有3，5，7 阶等不同阶数区别，阶数越大椭圆面积越大，根据不同的应用需求规定色度的椭圆阶数大小，图中所展示为3 阶麦克亚当椭圆。LED封装器件最终成品测量下来的色度坐标如果偏出指定的椭圆范围，则会被判定成不合格品，对生产企业造成直接经济损失。

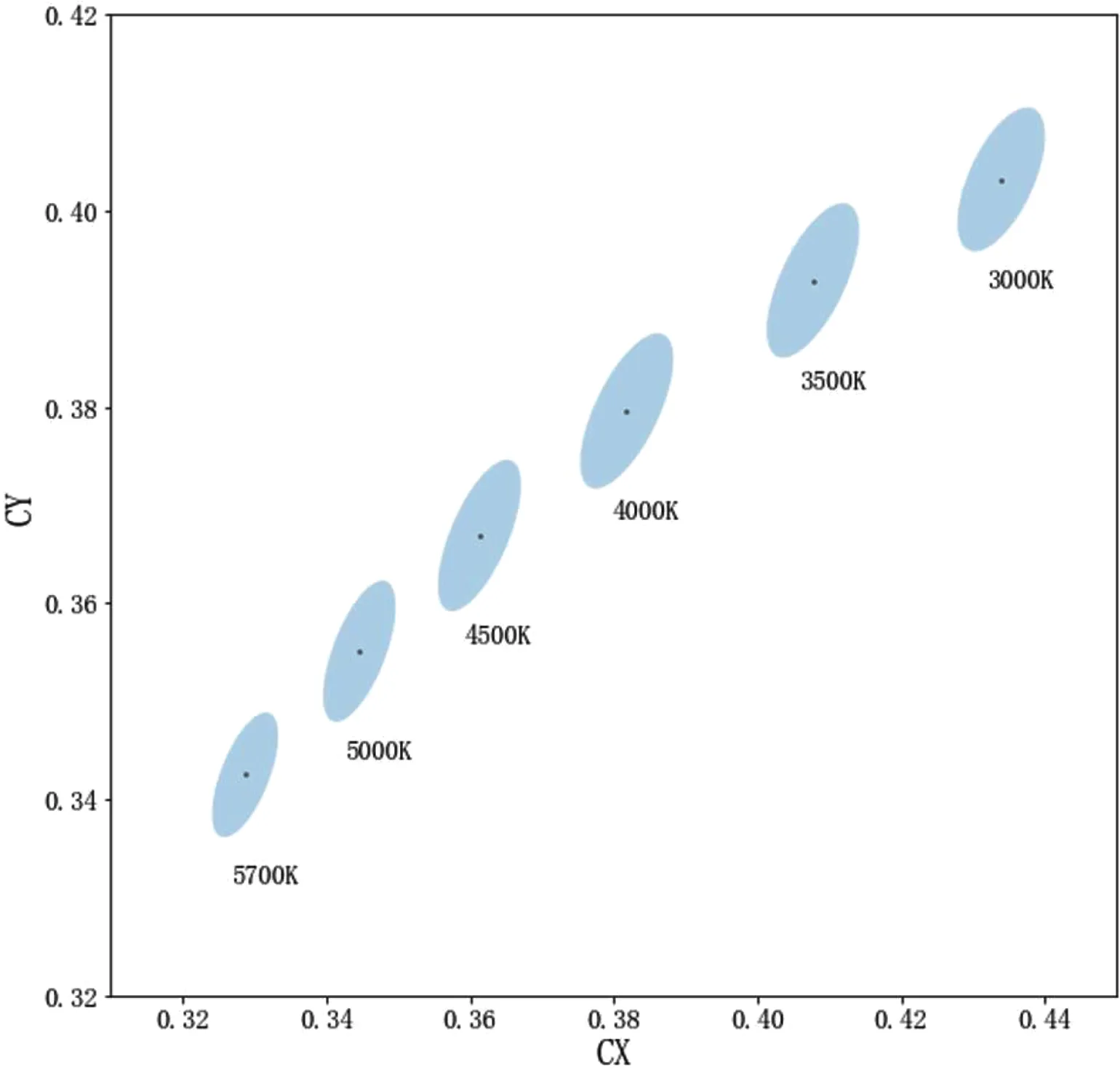
图1：LED 不同相关色温的3 阶麦克亚当椭圆

LED封装作为LED 光源生产中的重要环节，很大程度决定了最终光源的发光质量。本文探讨对象为大功率白光LED 器件，其封装过程中荧光粉涂覆采用雾化喷涂工艺，因荧光粉在透明硅胶溶剂中的浓度不变，影响发光色度的主要因素有荧光粉硅胶的涂覆量[3-4]，另外还有增加引线框架反射率的TiO2 硅胶涂覆量[5]，以及器件所使用的蓝光芯片的发光亮度与主波长。因此通过收集这些关键的材料信息与封装工艺数据，并加以充分的分析利用，可以实现过程中对最终光源色度的准确预测。LED 的封装生产周期较长，当生产过程中拥有可靠准确的预测手段时，可以及时预警异常并采取相应的补救措施，避免了后续大批量不合格品的产生，这对企业提升良品率以及保证订单交付有着重要的意义。

关于数据的分析及预测方面，文献[6,7]提出了一种基于k-means聚类与SVM 回归的方法，分别应用在对机场噪声，光伏发电功率的预测中，通过k 均值算法对历史数据进行聚类，然后在各个类别上分别训练支持向量机（SVM），对比直接使用SVM 模型，预测准确度有了明显提升。文献[8]利用高斯混合模型，根据历史风力输入和电力输出数据，将风电场内发电机组进行了分类，选择代表机组进行回归训练，提高了预测准确性和时效性。

目前企业在LED 的荧光粉涂覆完成后抽样检测半成品色度，对半成品色度及最终成品色度关系直接采用神经网络进行拟合，该方法生成的预测模型忽视了LED 芯片特征和封装状态的差异，训练后得到的笼统的单个模型在预测准确性方面有所欠缺。本文采用高斯混合模型（Gaussian mixture model, GMM）对LED 芯片特征和封装过程中的工艺数据进行聚类，首先利用贝叶斯信息准则（Bayesian information criterion, BIC）判定最优聚类个数，然后通过最大期望（Expectation maximization, EM）算法进行聚类，最后依靠反向传播（Back propagation, BP）神经网络对各个类别进行回归运算,最终模型能够准确地预测白光LED 色度，验证所提方法优于直接回归和k-means 聚类后回归方法，为LED 色度预测提供了有效的思路。

1 聚类分析

1.1 高斯混合模型（GMM）

1.1.1 模型理论及实现算法

高斯混合模型是通过多个高斯分布函数的线性叠加来拟合样本分布，假设样本数据集合服从k 个参数未知的高斯分布，服从相同分布的样本会被划分到一类。本文利用最大期望算法[9]对高斯混合模型的参数进行估计，求出每个分布各自的均值和协方差，具体流程如下。

第一步：初始化k 个高斯分布各自的均值μj和协方差∑j，分布的权重φj初始值设定为1/k，其中1 ≤j ≤k。

第二步：按照公式（1）和公式（2）估计每一个样本点xi（样本点数量为m, i=1,2,…,m，）属于的j 类高斯分布的概率γi,j,。

式中N(﹒)为概率密度函数；d 为xi的维度。

第三步：按照公式（3），公式（4）和公式（5）更新各高斯分布的参数μj，∑j，φj。

第四步：重复第二步和第三步，直到各个高斯分布参数收敛。

第五步：按照样本点概率γi,j的最大值对样本点进行归类

本文选取LED 芯片亮度，波长，荧光粉硅胶涂覆量，TiO2硅胶涂覆量，半成品色度坐标（CX, CY）这些数据的中位值作为各个封装批次的特征，共7 个维度，高斯混合聚类模型将这7 维特征作为输入数据对各个封装批次进行分类。

1.1.2 混合模型组数的确定

基于贝叶斯信息准则[10]来确定高斯混合分布的分组数量。BIC值的计算公式中包含似然函数项和惩罚因子项，公式如下：

式中Ln(L)为样本点集合的高斯混合模型的极大似然函数；np为混合模型中的参数个数；m 是样本点个数。

公式中Ln(L)数值越大，BIC 值越低，表示模型对样本点分布的拟合效果越好，同时np作为惩罚因子起到防止模型过拟合的作用，因此通过计算不同组数的BIC 数值，优先寻找低BIC 值的分组数量。

1.2 k-means算法及轮廓系数

广泛应用的k-means 聚类方法是通过计算样本点到每一类别中心的欧式距离，然后按照距离最小的原则进行类别判定，本文采用k-means 聚类方法同步建立分组模型，与GMM 方法做后续预测结果的对比。

k-means 聚类的分组个数利用轮廓系数（Silhouette coefficient，SC）作为评价分组合理性的指标，SC 值公式如下：

式中a(xi)为样本点xi 与同组内其他点距离的平均值；b(xi)为样本点xi与最相邻的其他组内样本点距离的平均值。

SC 值的取值范围为[-1,1]，SC 值越大，说明同组样本相距越近，组间样本相距越远，分组效果明显。因此在使用k-means 聚类选择分组个数时，优先寻找高SC 值的组数。

2 建模步骤

封装批次分组完成后，在各组上分别建立预测模型，图2 为先聚类后预测的模型建立流程。详细步骤如下：

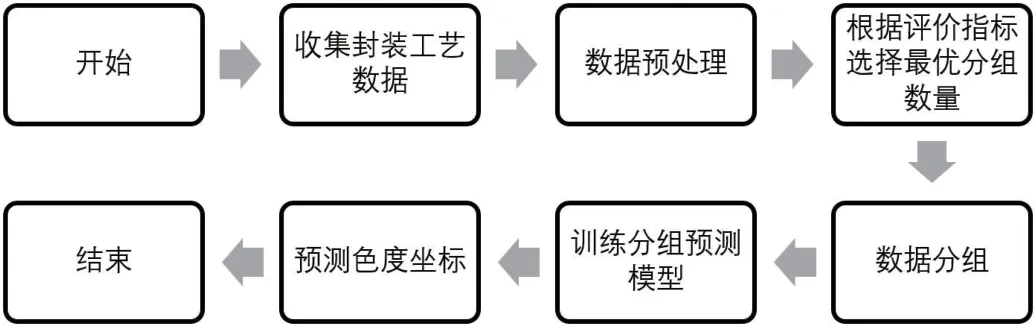
图2：先聚类的色度坐标预测流程图

（1）选取影响发光色度的关键工艺参数作为输入特征，清洗异常数据，并做数据归一化，减少参数间数量级的差异；

（2）基于BIC 值或SC 值选取最优的分组方案，利用聚类算法对各批次按照特征数据进行分组；

（3）以荧光粉喷涂完成后（半成品状态）抽样检测的色度坐标作为输入，分别训练各组的预测模型，使用训练完成的模型预测最终成品的色度坐标。

本文色度预测模型通过BP 神经网络[11]构建，BP 神经网络是一种按照误差逆向传播算

法训练的多层前馈神经网络，是目前应用最广泛的神经网络模型之一，其优点就是具有很强的非线性映射能力。神经网络的隐藏层层数、各层的神经元个数可根据具体情况设定，并且网络结构的差异导致其性能也有所不同。本文通过网格搜索选择最优的隐藏层层数和隐藏层包含的神经元个数,对分组后的数据分别构建预测模型。

3 实验分析与讨论

为了验证模型的有效性，本文共收集白光LED 的4 个CCT 共653 个封装批次的数据，每批次单颗颗粒的成品测试数据1400 个，半成品抽样测试数据480 个，芯片亮度波长数据1400 个，均按批次合并取中位值。荧光粉涂覆量，TiO2硅胶涂覆量则使用设备记录的批次数据。将样本数据按照80%，20%的比例拆分为训练集和测试集。

3.1 数据预处理

因为系统和机台记录故障，通讯异常，或者测试时接触不良的情况，产生了许多非正常的生产数据，异常数据对于预测模型的有效性和准确性有较大影响，根据异常数据的分布特点，使用基于密度的局部异常因子（Local Outlier Factor，LOF)[12]算法对数据进行清理，该方法将当前点密度明显小于领域点密度判定为异常点，以收集的半成品色度坐标为例，使用该方法清理前后的数据如图3所示。

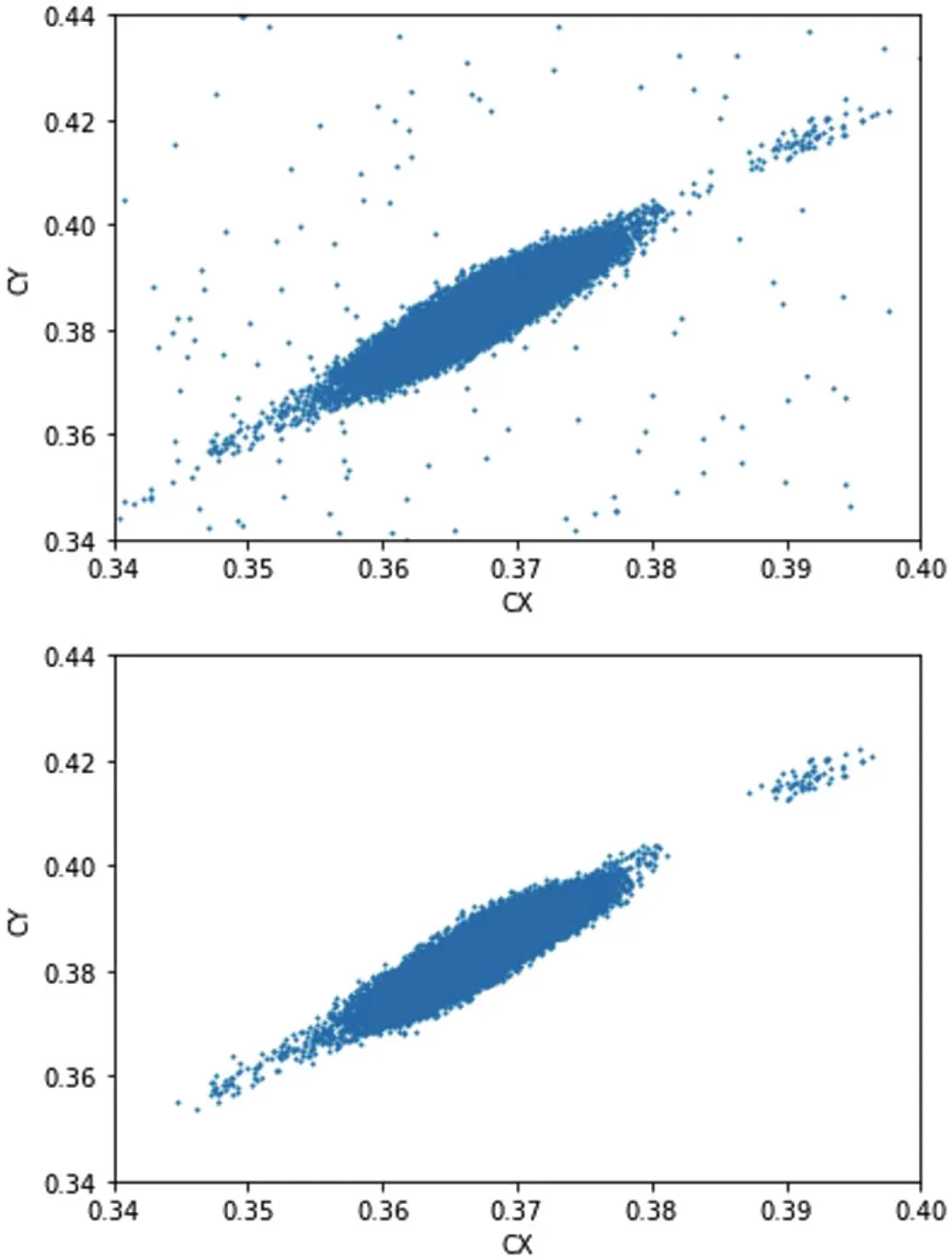
图3：半成品色度坐标数据清洗前后

去除异常点后需要将数据进行标准化处理，本文采用0-1 标准化将样本每个特征都转换为均值为0 和方差为1 的分布，公式如下：

其中μ 为某一样本特征的平均值，σ 为标准差。

3.2 数据分组

利用LED 芯片亮度，波长，荧光粉硅胶涂覆量，TiO2硅胶涂覆量，半成品色度坐标这些数据作为封装批次的特征，对各批次进行分组。使用EM 算法分别按照GMM 分组个数2 到10 时进行聚类，计算不同分组数量时对应的BIC 值，另外作为对比算法，也计算了k-means算法按2 到10 组聚类，各种分组数量下的SC 值。BIC 值和SC 值根据不同分组个数的变化如图所示。

由图4可以看到，随着分组数量的增加，BIC数值先降低后升高，在分组个数为3 时达到最低值2488，而SC 值则是分组个数为4 时达到最大值0.32.根据最优的聚类数量的判断规则，取BIC值最低时，即分组数量3 作为GMM 最优聚类数量，取SC 值最高时，即分组数量4 作为k-means 最优聚类数量。

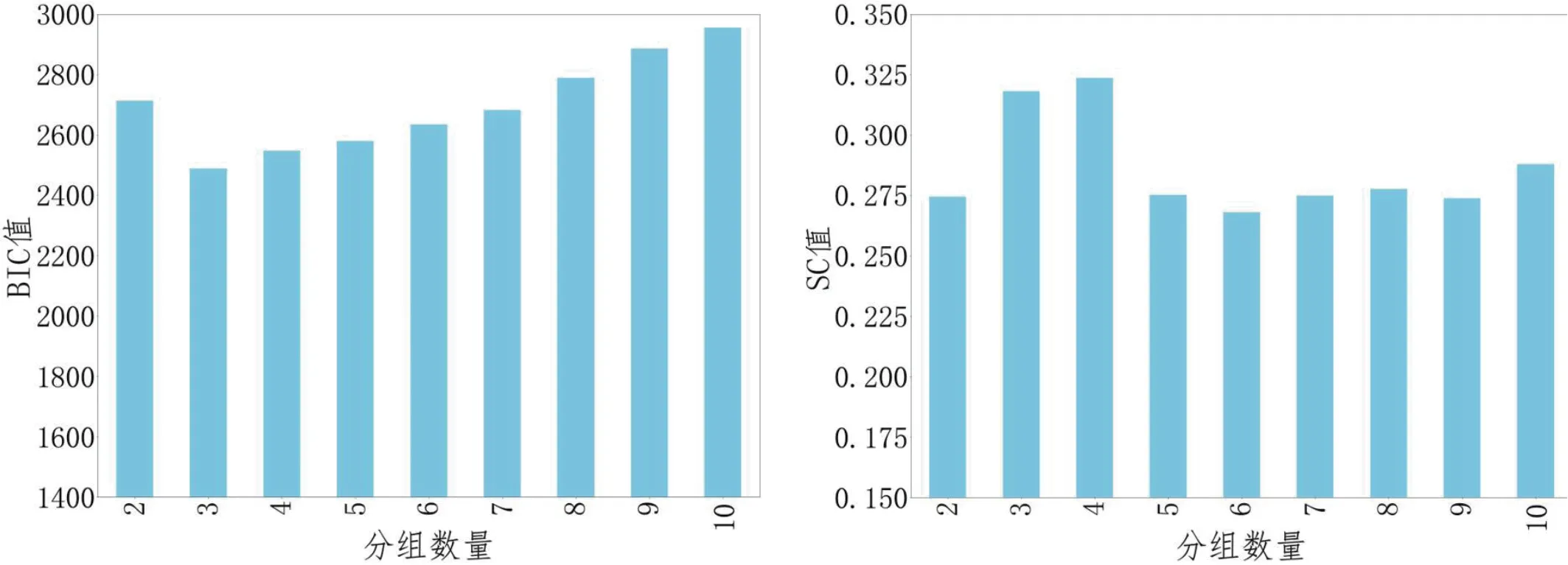
图4：GMM 分组的BIC 值和k-means 分组的SC 值

3.3 实验结果分析

训练集上的封装批次分组完成后，使用LED 半成品的色度坐标和成品色度坐标分别作为BP 神经网络的输入和输出，进行组内训练。在测试集上使用训练完成后的模型预测成品色度坐标，验证模型的准确性。实验选取RMSE(Root Mean Squared Erro,均方根误差)与R2值作为评价模型准确性的指标，RMSE 表示开根号的输出与目标之间平均平方差，值越小则表明仿真得到的模型越精准。R2值则是对比预测模型与基准模型（取平均值预测）好坏的指标，R2取值从负无穷到1，数值越大说明预测模型较基准模型优势明显，拟合效果越好。RMSE 值和R 值的计算公式如公式（9）和公式（10）所示：

以相关色温5700K 为例，表1 是按照评价指标对比不同模型预测结果，未分组的BP 网络，GMM 分组和k-means 分组得到色度坐标CX 预测的RMSE 值分别为0.0013，0.0009 和0.001，可以看到GMM 分组后的预测效果最好，较未分组的BP 网络和k-means分组预测值RMSE 指标分别降低了44%和11%，色度坐标CY 上分别降低了50%和14%。另外从R2值方面，GMM 分组后色度预测结果R2 值最高，其中CY 预测上R2值达到了0.804，同样证明了模型的预测效果优秀。

表1：不同模型的成品CX，CY 预测RMSE 值和R2 值对比

图5 是使用不同算法预测色度坐标CXCY 数值的折线图对比，从中也可以看到GMM 分组后的预测模型折线更加贴合实际值，预测的准确度较高。

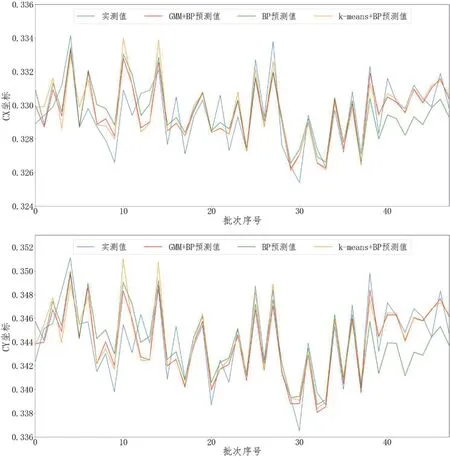
图5：各批次成品的CX，CY 预测值与实际值

除了在色温5700K 上，从其他色温的预测结果来看，GMM 分组后的预测网络同样具有较好的准确度，另外分别计算了相关色温4000K，5000K, 6500K 上不同预测模型的色度RMSE 值，如图6 折线图显示，GMM 分组后的预测结果始终好于未分组和k-means分组后的预测，而且在5000K 的色度预测上最优，CX 和CY 的RMSE 值较未分组的BP 预测结果降低了21%和53%，准确性提升明显。在3000K 和4000K 的CX，CY 预测上各算法结果比较接近，GMM 分组算法稍好于其他算法。因此，可以看到GMM 分组后的预测网络在各个色温上的预测，具有最好的稳定性，适用于各个相关色温的色度预测。

4 结束语

由于影响大功率白光LED封装器件色度的因素较多，如蓝光芯片的波长、亮度，还有荧光粉涂覆量，TiO2硅胶涂覆量等，因此本文在对LED 色度的预测中引入了聚类分析，通过EM 算法来对LED封装批次特征数据进行GMM 聚类，然后分别对各个类别进行BP 神经网络回归计算，实验结果证明该算法可以有效地提高预测的精确度。使用RMSE 值和R2值作为评价指标，对比直接回归和k-means 聚类后回归，本文方法在评价指标上均优于这两种方法。另外应用在各个相关色温的色度预测上，GMM 聚类预测模型也表现出更优的准确性和稳定性。本文为白光LED封装器件色度的准确预测提供了新的思路，后续可以不断地将最新样本数据加入模型，使得模型能适应变化的生产线状态，以保持较好的预测精度。