基于场路耦合低值绝缘子串温度分布研究

2021-03-06夏凡

电工材料 2021年1期

夏凡

（三峡大学电气与新能源学院，湖北宜昌 443002）

引言

绝缘子是输电线路的重要组成部分，其对保障输电线路电气性能起关键性作用，其绝缘有效性关乎输电线路的安全运行。瓷质绝缘子在长期运行过程中容易受到机电联合作用发生机械性能和绝缘性能下降的情况，这种现象容易产生低值绝缘子。雷电、雨天时，低值绝缘子容易受到雷击，其表面将产生强大的电流，电流的热效应容易使低值绝缘子发生断裂事故[1-3]，对电力系统的稳定运行造成严重威胁。

文献[4]研究了绝缘子性能劣化时，其温度将发生改变，为研究绝缘子热故障提供了理论支持；文献[5,6]研究了绝缘子表面电导率对绝缘子串温度分布的影响；文献[7]针对干燥带在绝缘子表面发热机理进行了研究，并得出干燥带长度、宽度以及位置对绝缘子温度分布影响较大；文献[8]对绝缘子表面积污进行了温度场研究；文献[9]研究表明，当湿度发生变化时，绝缘子串温度也会随之改变；文献[10]利用电网络法对绝缘子的红外热像检测盲区进行了研究，量化了盲区的概念；文献[11]针对零值绝缘子红外检测盲区问题，提出了应用盘面特征识别来检测零值绝缘子。

上述研究绝缘子红外热像问题时，用传统有限元软件考虑杆塔计算对低值绝缘子串温度分布的影响较为复杂，计算成本高，且较少考虑多种因素的影响；而单纯利用电网络法参考绝缘子杂散电容经验值进行仿真存在一定问题，难以适应实际现场各种各样的环境和绝缘子串模型。故本研究以有限元软件与电网络法相结合，以杆塔7片绝缘子为例，首先通过Maxwell电容矩计算110 kV绝缘子杂散电容，结合电网络利用MATLAB计算绝缘子阻值对绝缘子串电压分布影响，进而讨论低值绝缘子阻值及其位置，风速、测量误差对含低零值绝缘子温度分布检测的影响。

1 绝缘子杂算电容理论分析

以常见的瓷绝缘子为例，每片绝缘子由钢帽、钢脚、伞裙组成，水泥粘合剂连接其组合部分。其中钢帽、钢脚作为绝缘子中导体部分，在计算绝缘子串杂算电容时可以将其视为一个导体。在一个绝缘子片数为n的塔-绝缘子-导线系统中，每片绝缘子钢帽和上一片绝缘子钢脚相连，绝缘串上金具和杆塔相连，绝缘子串下金具和导线相连。为方便计算杂算电容，可以分别将其视为导体，由于杆塔为零电位，可以将杆塔为参考地。在绝缘子片数为n的塔-绝缘子-导线系统中有n个导体，假设任意一个导体上的电荷为Qi，电位为Ui，其中i=1、2、…、n。Ci0为导体i对地电容，Cij为导体i和导体j之间相互电容。所以在塔-绝缘子-导线系统中，各导体上电荷、电容、电位之间满足如下关系[12]：

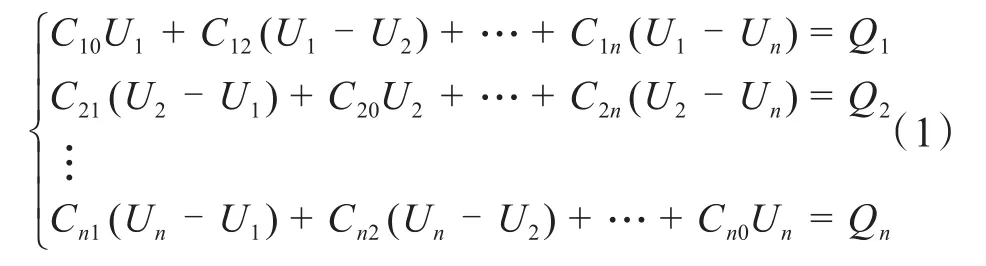
将式（1）以矩阵形式表述为：

矩阵C中有：

矩阵C对角线上元素的值Cii为相应导体对系统中所有其他导体的部分电容和。故导体i对地电容为：

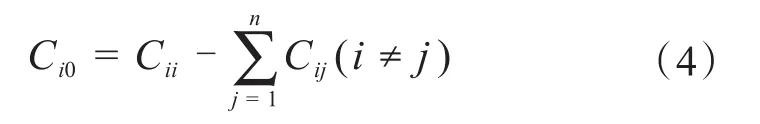
假设高压导线为导体n，则导体i(i≠n)对导线n的电容为Cin，即各片绝缘子对导线的杂算电容为矩阵Cin。

2 110 kV直线猫头塔瓷绝缘子串模型

2.1 模型建立

110 kV直线猫头塔带中相瓷绝缘子串的杆塔选择B7型直线杆塔，以圆柱体分别模拟金具和导线，绝缘子采用 xp-160瓷质绝缘子，xp-160 瓷质绝缘子具体技术参数见表1，各部分材料介质的相对介电常数见表2[13]。

表1 XP-160绝缘子技术参数 mm

表2 各介质材料相对介电常数

2.2 杂散电容计算

采用comsol软件计算麦克斯韦电容矩阵。为计算麦克斯韦电容矩阵，需要对各导体电压进行设置，由于各导体电容大小与自身结构和材料属性有关，与加在导体上电压高低无关，可对杆塔设置零电位，其他导体设置2 V，结合公式（1）～（4）计算麦克斯韦电容矩阵。其中以距离导线最近绝缘子为1号绝缘子，其余绝缘子编号以此类推，通过仿真计算，各片绝缘子对地电容和对导线电容分别如图1、2所示。

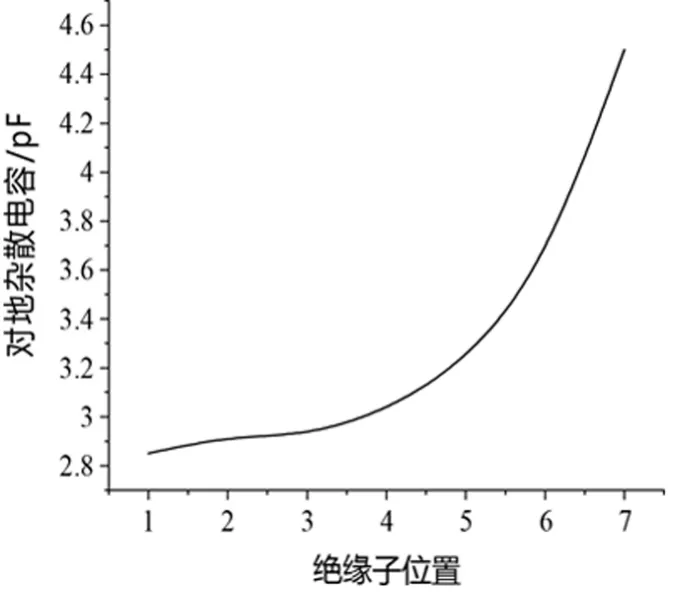
图1 对地电容分布

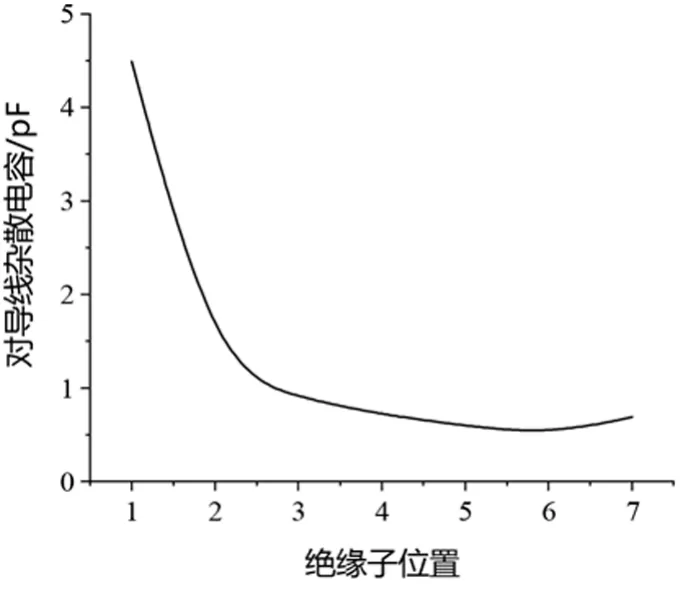
图2 对高压导线电容分布

从图1、2可以看出，绝缘子对地杂散电容和对导线杂散电容值总体满足电容值与距离呈非线性关系。绝缘子距离杆塔横担、导线距离越远，杂散电容越小，其中绝缘子对地杂散电容最大值与绝缘子上方金具长短有关，金具越长代表绝缘子最上片与横担距离越大，相应绝缘子对杆塔杂散电容越小；同理绝缘子对导线杂散电容最大值与绝缘子下方金具长短有关，绝缘子下方金具越长，相应绝缘子对导线杂散电容越小。

2.3 绝缘子串路模型及其电压分布验证

单片绝缘子可以等效为电容和电阻的并联，故110 kV杆塔7片绝缘串可建立如图3所示的等效模型。

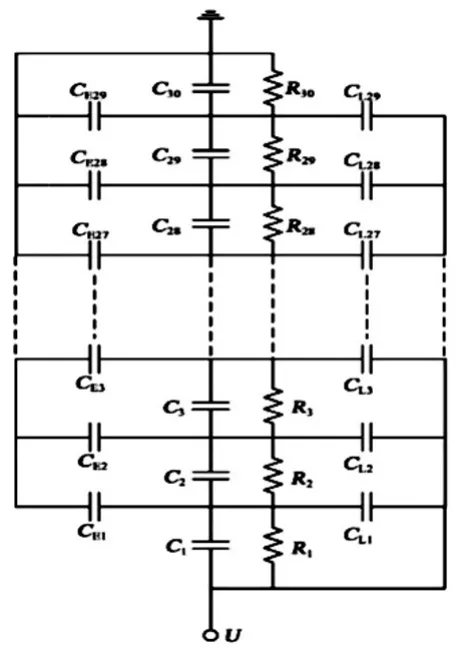
图3 绝缘子等效电路图

依据图3绝缘子串等效电路图，在MATLAB建立绝缘子等效电路模型，参考文献[14]中测得绝缘子自身电容为50 pF，杂散电容由comsol电场计算获得。绝缘子在洁净情况下，电阻很大，取绝缘子自身电阻为10 GΩ，绝缘子等效电路模型中U设置为63.5 kV，利用MATLAB计算110 kV杆塔7片绝缘子串电压分布，并与实际测量值、有限元仿真软件仿真值进行对比，如图4所示。从图4可以看出，MATLAB计算值、实际测量值和有限元计算绝缘子电压分布值均满足U型分布，并且这3种计算结果均相差无几，从而验证场路耦合在计算绝缘子分布电压具有可行性和正确性。

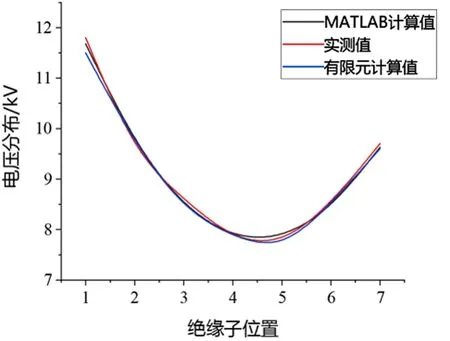
图4 与实测电压分布比较

3 低值绝缘子对绝缘子温度分布影响

在低于500 kV输电线路中，当瓷悬式绝缘子被检测电压低于50%标准规定值或者所测量绝缘子阻值低于300 MΩ时，将被判定为劣化绝缘子[15]。取靠近导线侧绝缘子为1号绝缘子，分别取1号绝缘子为不同阻值，计算不同阻值对绝缘子串电压分布的影响，如图5所示。

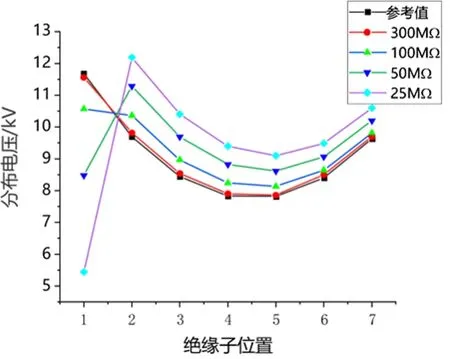
图5 1号绝缘子不同绝缘子阻值对电压分布的影响

从图5可以看出，当1号绝缘子阻值为300 MΩ时，绝缘子串电压分布和正常绝缘子串电压分布并无明显差别，即300 MΩ并不能作为判定绝缘子发生劣化的依据，当1号绝缘子阻值为25 MΩ时，1号绝缘子分布电压相对正常绝缘子的分布电压下降约为50%，即该值可以作为绝缘子发生劣化判据。

3.1 绝缘子发热理论分析

内部穿透性电流发热、介质损耗电流发热和表面泄露电流发热是绝缘子发热的3个主要部分[16]，当绝缘子洁净时，绝缘子温升主要由介质损耗电流发热功率决定；当绝缘子表面污秽层湿润时，此时绝缘子发热主要由绝缘子表面泄露电流决定，但介质损耗电流发热功率仍然不可忽略。根据牛顿冷却定律，绝缘子相对环境温升可以表达为：

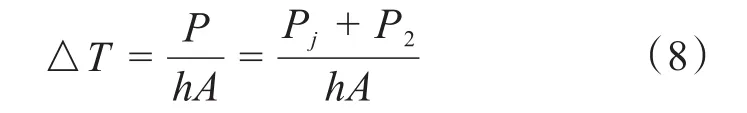
式中：A为散热面积，在该模型里指绝缘子钢帽面积，对于XP-160型绝缘子钢帽表面积A＝0.03 m2；h为散热系数，当温度在5℃～35℃、风速在0～0.2 m时，h为15 W/m2·℃。

3.2 低值绝缘子阻值对绝缘子温度分布的影响

分别对1号绝缘子取不同阻值，如图6所示。从该图可以看出，绝缘子整体温度分布呈现非线性分布，当1号绝缘子发生劣化时，对应温度高于整串绝缘子中其他位置绝缘子。其中，当1号绝缘子阻值为50 MΩ对应温度最高，参考值曲线中正常绝缘子温度最低。

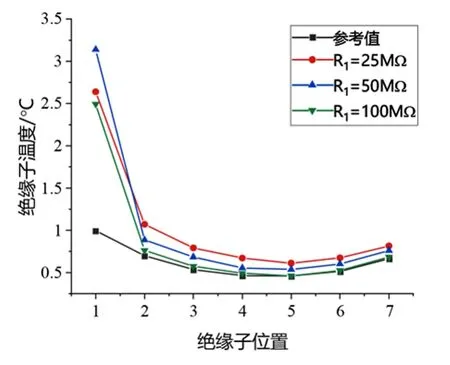
图6 1号绝缘子不同阻值温度分布

3.3 低值绝缘子位置对绝缘子温度分布影响

按照距离高压导线远近，取三个特殊位置绝缘子，分别为1号、4号和7号绝缘子，并令其电阻值为50 MΩ，得到同一阻值不同位置劣化绝缘子对绝缘子串温度分布影响，如图7所示。从图7可以看出当绝缘子发生劣化时，绝缘子串总体温升会抬升。这是因为绝缘子劣化时，绝缘子串总体电阻减少，导致绝缘子串温度抬升。绝缘子串发生劣化时，相对环境而言，首端绝缘子温度最高，最高可达3.4℃，尾端绝缘子温度次之，为2.5℃，中部绝缘子温度最低，最低为1.5℃。