一种解决专用道设置问题的分布式蚁群算法实现

曹明

（北京航空航天大学经济管理学院，北京100191）

1 背景

随着中国社会经济的发展，各种大型活动，如大型体育赛事、大型会展活动等经常在大城市举办。这样一方面使大城市的交通压力增大，另一方面因为大型活动对时间有严格的要求（比如2008 年北京奥运会就严格要求从运动员驻地到比赛场馆的行车时间要限制在30 分钟内），场馆到运动员驻地的交通必须保持畅通。要同时解决这两方面的问题，在城市交通基础设施不能短期内得到明显提升的前提下，实行必要的交通管制是一种行之有效的手段。为保证这类大型活动对时间的要求，交通管制一般的做法是在有多条车道的城市道路上划定专用车道，在某个时间范围内供大型活动的车辆使用，这种做法类似于城市的公交专用道[1,2]，如图1 所示。本文的研究目标就是这种专用道的设置问题。

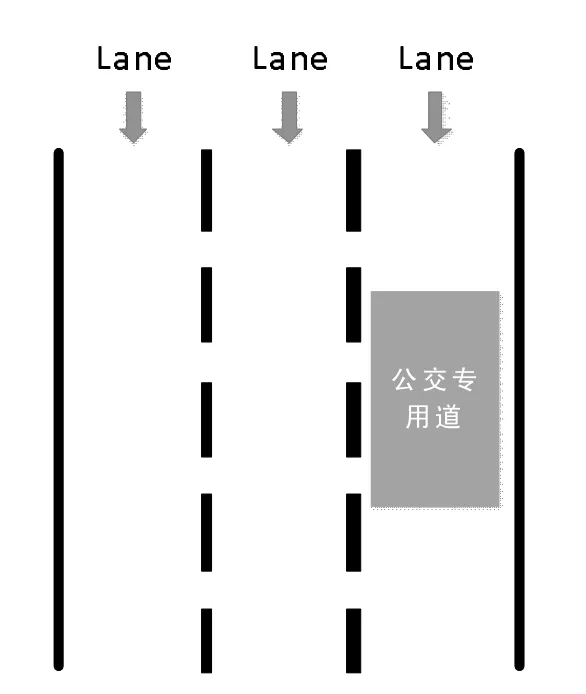
图1 城市的公交专用道示例

LRP（Lane Reservation Problem）即专用道设置问题[3-6]，是交通运输领域的热点研究问题之一。LRP 着眼于解决在哪些道路上设置专用道，可以满足诸如从运动员驻地到比赛场馆的最长时间要求的限制，同时尽量保证城市交通不受太大影响。LRP是组合优化问题，这类问题的算法复杂度通常都是NP-Hard的，需要综合交通、运筹学、计算机科学等多学科知识加以解决。由于LRP 的复杂性，对大规模问题，运筹学软件可能无能为力，即不可能在有限时间内找到最优解。这就需要采用启发式算法，在可以接受的计算时间内求得一个能够满足要求的次优解。

本文探讨在分布式计算框架Spark 下实现一个蚁群算法[7-11]，用于求解LRP 问题。首先描述了LPR 的数学模型，随后给出了分布式蚁群算法的实现方法。将该方法应用于现有的LRP，给出了实验结果。

2 数学模型

采用文献[3]中的LRP 的数学模型作为本文求解的模型。该模型是以2010 年广州亚运会的道路网络图为基础构建的，如图2 所示。图2 包括一个表示运动员驻地的顶点（起点），多个表示比赛场馆的顶点（终点），多个表示途中各个岔路口的顶点（中间节点），以及表示这些点之间道路的弧。从图2 可以看出，从运动员驻地到任何比赛场馆都存在至少一条可通达的路径。图3 中用到的式（14）定义：

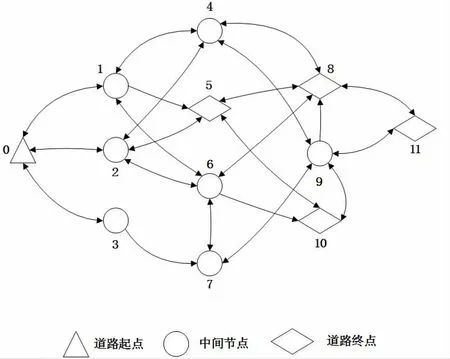
图2 运动员驻地到比赛场馆的道路网络图

3 分布式蚁群算法的实现

从上述LRP 模型可以知道，求解该模型的关键是找到从起始顶点到目标终点的一条无回路的行驶路径。可以利用蚁群算法的生物特性，假定有一只蚂蚁从起始顶点走到目标终点且不产生回路（无环），那么这只蚂蚁走过的路径可以作为一条备选路径，再继续考察是否要在这条路径上设置专用道即可，问题就简化成了一个背包问题。

根据蚁群算法的信息素更新来指导每次迭代中每只蚂蚁的道路选择。因为算法使用Spark 计算框架实现，故这里直接给出在Spark 框架下蚁群算法的工作流程，见图3 中的伪代码。

图3 蚁群算法在Spark 框架下的伪代码

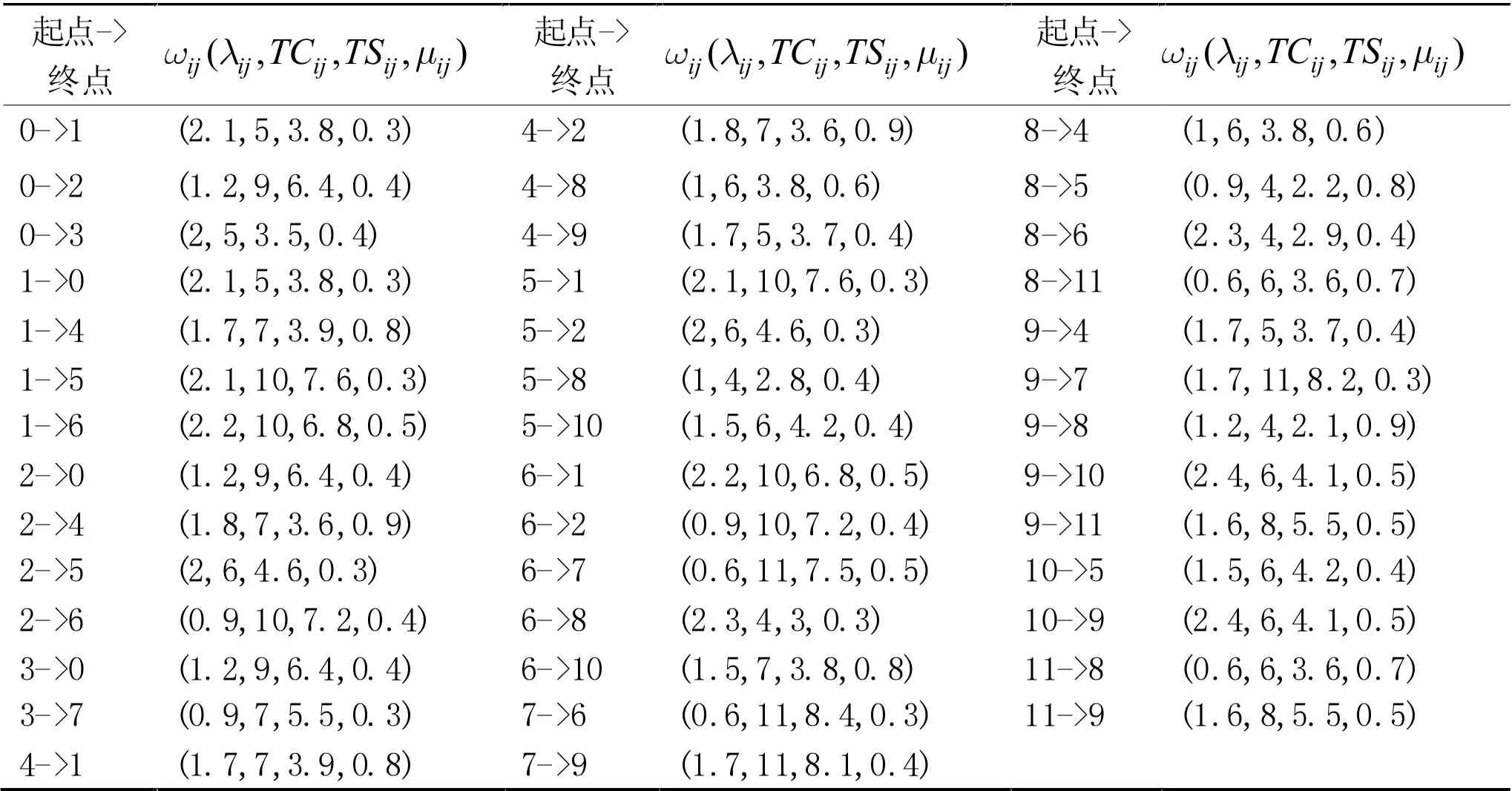
表1 交通网络图中弧(i,j)上信息示例：ω ij (λ i j ,T C ij ,T Sij , μij)

4 实验结果

实验结果在Intel Core I9 的电脑上以Spark 中的本地运行local[8]的方式运行获得，即默认使用8 线程并行计算。

采用上述蚁群算法，本文在迭代3 次、每次使用3 只蚂蚁的条件下，求出了该LRP 模型在时间约束C=30 分钟下的一个次优解，如表2 所示。

表2 时间约束C=30 分钟下的一个次优解

又随机做了10 次迭代，每次使用10 只蚂蚁，得到了另一个次优解,如表3 所示。

表3 时间约束C=30 分钟下的第二个次优解

从两个次优解可以看出，在约束C=30 分钟的情况下，可以求出不需要设置专用道的、符合赛会行程时间限制的次优解，也就是从运动员驻地到比赛场馆，若按照可选择的路径行驶，就没有必要设置专用道，正常通行即可，不会对城市交通带来影响。

为考察算法对大规模问题的求解效率，本文将网络图的顶点个数调大，由Spark 的Graphx 自生成图的方式，生成不同顶点个数的网络图，然后采用蚁群算法计算，得到的顶点个数和算法运算时间的关系如图4 所示。从图中可以观察到，顶点个数和运算时间的曲线呈现多项式关系。

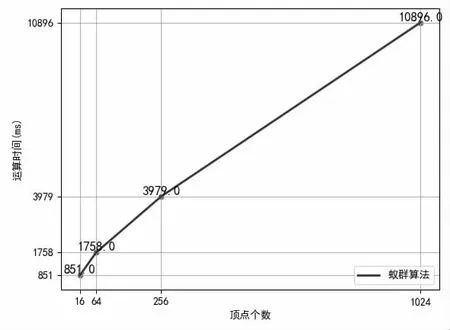
图4 顶点个数和运算时间的关系图

5 结论

本文阐述了LRP 的研究背景和数学模型。LRP 是一个复杂度为NP-Hard 的问题，用传统算法无法在多项式时间内求出精确解，因此需使用启发式算法对LRP 问题求得满足约束条件的次优解。为此，本文在Spark 计算框架下设计了一种分布式的蚁群算法。通过实验发现，该算法可以有效求得模型的次优解。对于大规模LRP 的求解，本文用设计的蚁群算法计算并比较了不同的网络顶点个数对应的运算时间。从结果可以看出，网络顶点个数和运算时间呈多项式关系。