基于非线性拟合方法的雷达探测俯仰角估计

薛立娟 邱旭阳 李骁骅 张博阳

（1、北京机械设备研究所，北京100854 2、成都博芯联科科技有限公司，四川 成都610000）

1 概述

为了应对无人机的低成本化带来的安全问题，国内外都在研发低、慢、小监视系统，其中低空监视雷达是侦查分系统的核心。雷达应具备尽可能大的俯仰视角和测角精度。

传统和差单脉冲测向方法的精度取决于查找表与实际天线和差输出的一致性。通常采用暗室测试校准和标校塔外场校准两种方式。暗室测试校准法将雷达系统放置于暗室中，由雷达目标模拟器产生特定的目标信号，由精密转台或机械手转动天线阵面，记录不同角度下天线的和、差通道输出幅度和相位，形成查找表。对于无法放入暗室的雷达系统则采用位于室外开阔场地的标校塔，雷达信号模拟器放置于标校塔顶，获得查找表的测试方法与暗室测试校准法相同。

既有的方法大多数采用幅度- 相位数字校正方式实现角度估计的精度提升[1-2]。对低空雷达，此类方式局限性在于：（1）低空雷达的目标角度低、回波信噪比低，在理想环境（暗室、测试场）中校准结果很难适应目标的回波闪烁效应，误差较大；（2）低空雷达通常移动部署，部署环境条件、周边地物差异甚大，试验场标校结果不一定普遍适应，仅通过上位机软件修正，难以达到最优效果，尤其是部署调试流程难以标准化，模板化。本文提出一种基于非线性拟合方法的俯仰角估计，不仅可以提升测角精度，也可有效解决测试场标校方法的问题。

2 雷达工作方式

低空雷达精度受低角度闪烁效应影响，严重时可造成目标完全无法跟踪，且地形越复杂，影响越剧烈，其有效解决方式为收窄雷达波束宽度或采用双波段收发机方案[3]。对低空雷达应用场景，目标最大飞行高度小于1000 米，典型飞行高度120 米，低角度观测几乎覆盖其主要有效距离范围。

本文雷达工作频段选择在Ka 波段实现窄波束宽度，结合有源相控阵实现大视角。系统天线采用16 元一维均匀喇叭阵，在雷达俯仰向做波束合成，在水平向采用一维抛物面实现水平向波束聚束。此时，系统水平波束固定，俯仰最大波束偏转角度（天线增益下降1dB）设计值为25°，电控波束调整范围可满足-50°～+50°。这种方案硬件加工复杂度低，对零件加工及装配精度容差可达±0.7mm，结构简单可靠，重量轻。一维相控阵，阵元总数量相比二维阵大大减少，即使采用收发独立的连续波体制，较二维阵仍有极大的成本优势。相控阵在水平维度采用一维转台机械扫描的工作方式见图1，可覆盖360°全向，以实现目标的XY 坐标定位。相控阵在俯仰维度做电控扫描，实现目标的Z 坐标定位。雷达阵面仰角为机械固定，其中阵面法向（相控阵偏转0°位置）与安装水平面（与地平面平行）的夹角定义为雷达机。

3 非线性拟合法俯仰角估计

3.1 目标偏角与和差比的关系

目标俯仰角估计方式采用和差波束测角方法，取得偏角信号的基本方法是：将天线阵分成两个相同子阵，将两个子阵同时收到的信号进行矢量相加与矢量相减处理，处理结果分别称为和通道输出、差通道输出[4]。利用和输出、差输出的幅度差确定目标偏离波束中轴线的角度，相位差确定偏离中轴线的方向。设两个子阵方向性函数F(θ)近似高斯函数，在单站工作模式下，子阵波束相对于天线的偏角δ=θ0.5，则对于偏离天线轴的目标，其和通道回波振幅为：

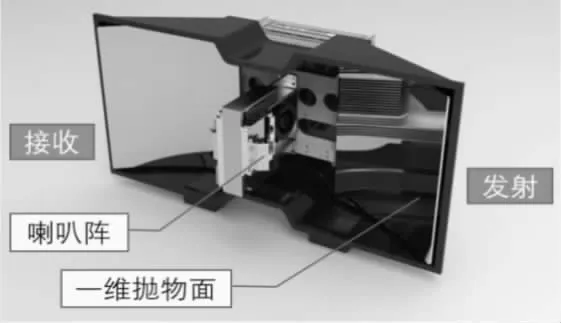
图1 一维线性阵三坐标雷达示意图

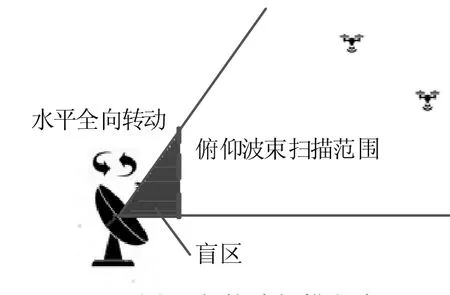
图2 相控阵扫描方式

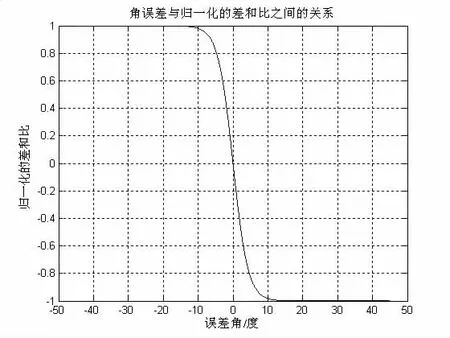
图3 角误差与归一化和差比函数图

以上两点可以归结为在多个随机因素影响测量的情况下，利用实测数据，对和差幅度差- 目标偏角函数进行参数估计。针对上述特点提出使用非线性拟合方法进行俯仰角度计算。

3.2 俯仰角非线性拟合实现

初始条件：a.校正雷达安装平台法向与重力线垂直，控制安装误差不超过雷达测角误差的10%；b.无人机按固定路线，固定高度飞行，起飞点在雷达正上方；c.存储雷达数据，信息包含目标空距、波束预置位号、和差通道幅度差、和差通道角度差。

当前的商用无人机大多采取气压型高度计定高，高度误差典型值为0.5 米，典型飞行高度在数十米到数百米之间，故高度计误差可忽略不计，可认为其设定高度即为实际飞行高度。固定高度的无人机目标俯仰角为：

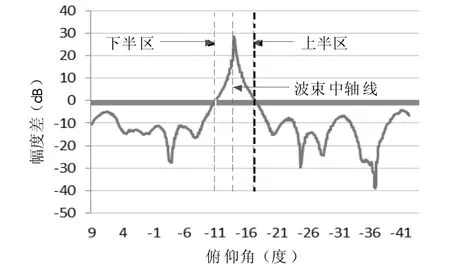
图4 回波幅度差曲线与俯仰角关系（1 号预置位）

拆分上下半区后，半区内数据集呈现出非奇异、非阶跃的特性，将其展开为非线性方程，将ΔA 与D 的映射函数F 重写为幂级数形式：

其中n 为最高次幂阶数，实际可通过实验比较，设定一个合适的阶数，保证拟合精度，又避免过度拟合。

4 角度估计实验结果

基于以上论证，本文基于Ka 波段雷达进行实验验证。测试点为城市边缘的复杂环境，存在大量树木、不规则地形、楼房等影响物体。测试参数为：测试分两组进行，无人机测试飞行高度分别为100m、300m，飞行速度10m/s，雷达定角度观察无人机并记录接收数字中频数据，进行拟合算法分析与结果验证。飞行数据集如图5、图6 所示，分别为无人机在100m 与300m 高度飞行时的雷达目标数据：

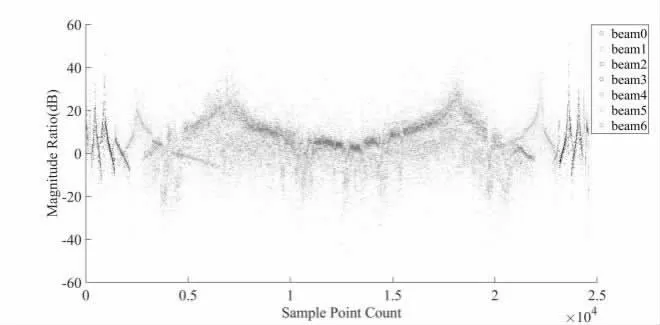
图5 无人机100m 飞行高度采集信息

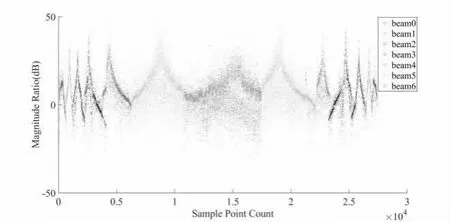
图6 无人机300m 飞行高度采集信息

根据图5、图6 所示数据结果，兼顾数据拟合的准确性与鲁棒性，本文采用3 阶多项式拟合，拟合后测试结果与理论计算的仿真如图7，图8 所示：

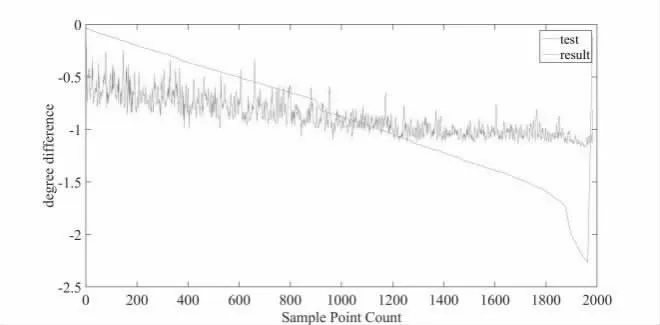
图7 拟合参数计算无人机俯仰角测试结果(预置位1)

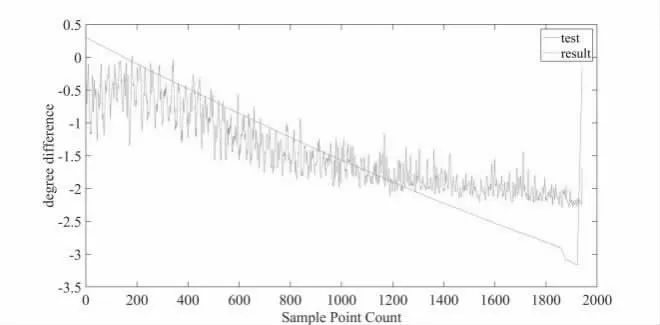
图8 拟合参数计算无人机俯仰角测试结果(预置位2)

从图7、图8 中可以看出利用上述方法计算无人机飞行俯仰角与理论误差均在1°范围以内，两图中前端数据误差大于1°，但是此处并未剔除偏差超过半区范围的点集（与中轴线角度差值大于3.25°），因此，虽然数据前端误差较大，但剔除半区范围外点集后，在±3.25°范围内的拟合误差均在1°范围以内。

5 结论

本文阐述了一种适用于低小慢监视雷达的俯仰角非线性拟合方法，该方法解决了在复杂环境下传统校准方式效果较差的问题，并且免去了暗室测试和标校塔测试带来的周期、人工、场地费用，降低了低慢小雷达的综合成本。通过连续波雷达进行俯仰角拟合试验验证了方法的有效性。此方法不局限于连续波雷达，亦适用于脉冲、步进频等各类体制雷达。