支持QoS的无线局域网自适应MAC协议算法*
2021-03-05邓皓文
邓皓文,江 虹,李 维
(西南科技大学 信息工程学院,四川 绵阳 621010)
0 引 言
随着网络服务种类增多,不同的服务具有不同的服务质量(quality of service,QoS)需求[1,2]。为此,IEEE制定了802.11e协议,其中的增强分布式接入(enhanced distributed channel access,EDCA)机制为数据流提供了QoS区分。但其参数不能随负载自适应变化,尤其是固定的退避机制在竞争站点较多的情况下会明显增加碰撞几率[3],使网络性能显著下降。国内外学者对如何改进EDCA的退避方式进行了大量研究,主要分为两大类:第一类是通过饱和吞吐量模型优化饱和吞吐量。文献[4~6]均是通过文献[7,8]中的饱和吞吐量模型来计算最优竞争窗口,使饱和状态下吞吐量接近最优。但是,以上方法的前提均是所有站点的业务都处于饱和状态,且需要准确估计竞争站点数目,求解复杂方程组,算法复杂度较高;第二类是通过网络负载因子调节竞争窗口来优化网络性能。文献[9]通过估计站点数目来动态调整竞争窗口的值。文献[10,11]通过监测时隙周期中的碰撞概率来自适应调整竞争窗口大小。文献[12]提出了GDCF算法,能有效降低网络碰撞,且额外开销较少,但不具有自适应性。
为了使EDCA机制能够适应网络负载变化,并针对目前大多数改进算法开销较大,不适用于无线传感器网络等场景,本文在GDCF基础之上提出了一种自适应退避算法。改进算法能够解决GDCF算法竞争窗口减小过慢的问题,进而降低网络时延,为高优先级业务提供更好的QoS保障。
1 EDCA机制简介
802.11e定义了8种流量种类(traffic category,TC),对应了4种业务接入种类(access category,AC),分别是语音业务(AC_VO)、视频业务(AC_VI)、尽力而为业务(AC_BE)、背景业务(AC_BK)。每个站点内部有4个AC队列,分别接收来自不同优先级业务的数据,每个AC队列形成“虚拟”站点,独立进行退避过程,有各自的仲裁帧间间隔(arbitration inter-frame space,AIFS),最小竞争窗口CWmin,最大竞争窗口CWmax和传输机会(transmission opportunity,TXOP)。高优先级业务有着较小的AIFS,CWmin,CWmax和较大的TXOP,因此高优先级业务有更大的几率竞争到信道,进而实现业务区分。EDCA机制的退避过程使用二进制指数退避(binary exponential backoff,BEB)算法,记b为退避阶段,第一次尝试发送MAC帧时,b=0,若发生碰撞,退避阶段加一,CW=2b*CWmin,当CW=CWmax时,竞争窗口不再增加。
2 自适应退避算法
2.1 算法思想
负载较重时,BEB算法成功发送数据后立即将竞争窗口重置到最小值,导致网络碰撞进一步加剧。文献[12]提出的GDCF算法,能够有效降低碰撞,基于GDCF算法,本文提出的自适应退避算法退避过程如图1(以6个退避阶段为例)。
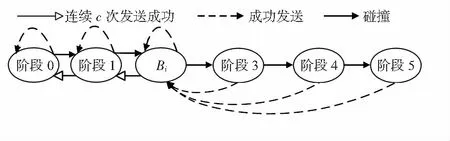
图1 自适应退避过程
在更新周期内,各优先级队列i记录每个数据包到达的最大退避阶段,得到每个更新周期内的平均最大退避阶段Bi。重置竞争窗口时,如果当前的退避阶段小于等于Bi,采用GDCF的窗口减小方式,如果当前的退避阶段大于Bi,将竞争窗口重置为2BiCWmin,相比GDCF有更快的竞争窗口递减速度。
2.2 改进算法具体描述
记Tupdate为数据包成功发送或者达到最大重传次数被丢弃时的时刻。定义更新周期为k个Tupdate时刻,bi为站点优先级业务i当前所处退避阶段,Si为累加变量(初值为0),Bi为优先级i的平均最大退避阶段,CW[i]为第i类业务当前的退避窗口,c为常数。k和c的取值将在仿真分析部分介绍。改进算法具体描述如下:
1)Si更新:当业务i处于Tupdate,根据当前的退避阶段,对Si进行更新,Si=Si+bi。
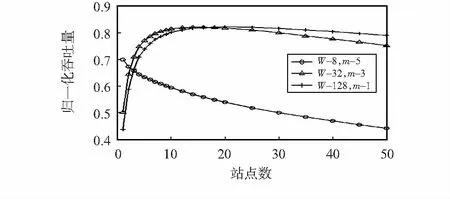
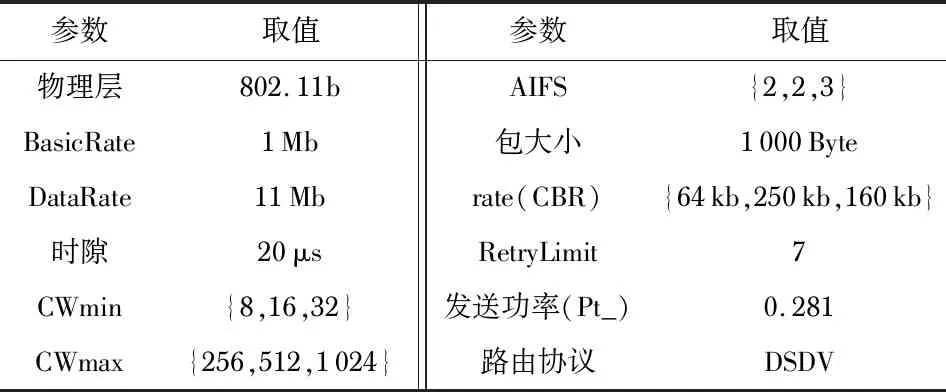
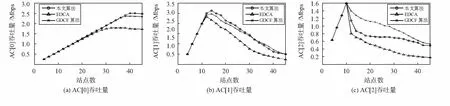
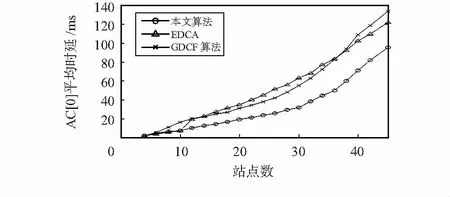
2)重置窗口:若bi,j 3)发生碰撞:CW[i]=2×CW[i],达到CW[i]max不再增加。 4)达到更新周期:计算出Bi=round(Si/k),并且令Si=0。 BEB算法的性能可由Bianchi提出的二维Markov链进行分析。为了简单说明问题,这里只考虑站点只有一个优先级业务i的情况。定义碰撞概率为pc,最大退避阶段为m,最大重传次数为l,Wi,0为最小竞争窗口,Wi,m为最大竞争窗口,可建立如图 2所示的二维Markov链。 图2 退避过程二维Markov链 (1) (2) 由Markov链稳态概率之和为1,有 (3) 文献[8]只考虑m=l的情况,这里考虑m有可能小于l的情况,由式(1)~式(3)可得 (4) 业务i发送数据的概率τ可以表示为 (5) 设共有n个站点,碰撞概率可表示为 pc=1-(1-τ)n-1 (6) 网络中有站点发送数据的概率可表示为 ptr=1-(1-τ)n (7) 网络中有站点成功发送数据的概率为[7] (8) 定义P为数据包长度,E[P]为数据包长度均值。Ts为成功发送数据整个过程所用时间,Tc为碰撞过程占用的时间,Tc和Ts的计算方法可参见文献[7]。σ为一个时隙的时间,整个网络归一化吞吐量S定义为[7] (9) 通过数值解法可以求解式(4)~式(6)构成的非线性方程组,得到不同n值下的pc和τ,进而通过式(9)计算出归一化吞吐量的值,详细计算参数可参见文献[7]。 当bi≤Bi时,减小竞争窗口,碰撞几率较高,此时采取GDCF的窗口递减方式。当bi>Bi时,重置窗口时令CW[i]=CW[i]min×2Bi,在CW[i]max不变的情况下,相当于增大了CW[i]min的值并减小了m的值。利用式(9)可以求解出不同最小竞争窗口W下的归一化吞吐量(Basic模式,最大竞争窗口为256),如图 3。 图3 不同最小竞争窗口下归一化吞吐量 可以看到,W为8时在站点数少的情况下吞吐量最高,但随着站点输增多,吞吐量会明显下降,此时W取较大值(32和128)能够显著提升网络吞吐量。这表明,站点数较多的情况下,增大W会减小碰撞概率,提高网络吞吐量;在站点数较少的情况下,较大的W会导致空闲时隙数增多,反而会降低吞吐量。因此,合理改变W的值能使网络具有自适应性。改进算法通过周期性更新Bi的值,重置竞争窗口时将退避阶段重置到Bi,相当于将最小竞争窗口动态调整到多个数据包发送成功时的平均竞争窗口,进而减小碰撞几率,提升网络性能。 使用NS—2.35来进行仿真,仿真场景大小为250 m×250 m,仿真参数见表1。网络中有多个静止站点和一个AP,站点在AP覆盖范围内随机均匀布置,站点仅与AP进行通信,形成星型拓扑结构,无隐藏站点,网络工作在Basic模式下。每个站点传输3种业务类型,分别是高优先级业务(AC[0])、中优先级业务(AC[1])和尽力而为业务(AC[2]),传输层采用UDP协议。每次仿真运行120s,结果取10次平均值。 表1 仿真用到的参数 首先,要选取合理的k值和c值。在网络饱和的情况下(站点数为30),选取不同k值进行实验,当k值取30时,饱和吞吐量接近最大,k大于30时,吞吐量不会有明显增加,因此,本文选择k=30作为统计周期。参考文献[12]建议,高、中、低优先级业务c值分别为2,3,4。 AC[0]的吞吐量变化如图 4(a)。原始EDCA机制在站点数大于20时AC[0]逐渐进入饱和状态;本文算法和GDCF能够降低网络碰撞,都能明显提升AC[0]吞吐量,GDCF在站点数为36时接近饱和,而本文算法在站点数为40时才接近饱和,这是由于GDCF竞争窗口减小过慢,AC[0]发送数据概率减小,抵消了减少碰撞带来的增益。在站点数为40的情况下,本文算法相对于EDCA和GDCF吞吐量分别提高了43 %和6 %。 图4(b)和图4(c)显示了AC[1]和AC[2]吞吐量随站点数目的变化。本文算法和GDCF算法AC[1]和AC[2]业务吞吐量明显高于EDCA。本文算法AC[1]业务吞吐量在站点数小于30的情况下明显高于GDCF,在站点数大于30情况下略低于GDCF;本文算法AC[2]的吞吐量较EDCA有明显提高,但低于GDCF。 图4 3种业务吞吐量随站点数目的变化 综合分析三种优先级业务的吞吐量,可以看到GDCF高优先级的业务的退避窗口减小过慢,使得低优先级业务有更高的几率竞争到信道。出现了本文算法AC[2]吞吐量不如GDCF的情况和站点数为30的时候AC[1]的吞吐量逐渐小于GDCF的情况,但本文算法AC[0]吞吐量始终高于GDCF算法。因此,本文的自适应算法相比于GDCF更能保证高优先级业务QoS。 AC[0]为时延敏感型业务,图5显示了不同站点数目下各种算法的时延。EDCA机制在站点数较多时,由于碰撞几率最高,时延最大。GDCF由于竞争窗口减小过慢,在站点数小于12时延最大;站点数大于12时GDCF能够有效避免碰撞,时延比EDCA小;站点数大于36时连续成功发送数据的概率变低,GDCF会将竞争窗口维持在较大值,此时低优先级接入信道的几率变大,导致退避时间过长,时延最大;本文算法平均时延最小,这是由于自适应算法既能够有效避免网络碰撞,且相比于GDCF能够避免竞争窗口下降过慢导致额外的退避时延。 图5 AC[0]平均时延 本文提出了一种支持区分服务的无线网络改进MAC协议,通过对EDCA机制中的退避算法进行改进,使得该机制具有自适应性。改进算法提高EDCA机制性能,在网络负载较高的情况下,降低了高优先级业务的时延,大幅提高了各优先级业务的吞吐量;改进算法相比于GDCF算法有更好的QoS区分和更低的网络时延。该算法额外开销较少,在需要电池供电的无线局域网以及无线传感器网络中具有一定的应用价值。3 理论分析
3.1 二维Markov链模型

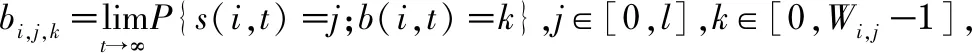
3.2 改进算法分析
4 仿真分析
4.1 仿真模型
4.2 仿真结果分析
5 结 论
