基于NARX-PSO-PID的绝缘厚度控制系统优化策略*

周克良,张宇龙,邹争明

(江西理工大学 电气工程与自动化学院,江西 赣州 341000)

0 引 言

线材绝缘护套挤出成型是线径控制系统的关键生产工艺。绝缘护套壁厚的精确控制是决定导线直径的关键技术[1]。电线挤出过程中,由于牵引设备和挤出机内的冷却系统(确保绝缘材料在挤出成型的温度范围)和所施加的牵引力及其变化模式从挤出机模具孔径不等于实际的外径的电线和塑料制品。

在工业控制领域中,对于绝缘电缆厚度控制[2～6]最经典的方法就是比例—积分—微分(proportional-integral-diffe-rential,PID)控制,但该方法的控制性能依赖于被控模型的精度以及PID的参数。首先对于PID三个参数的设置就是一个难点,另外控制过程中PID参数不能实时变化,导致控制器缺乏适应性。其次,对于绝缘电缆这种强滞后系统,只能通过挤出行程以及挤出速度来计算滞后时间,因此导致系统的响应速度慢,超调量大。因此部分学者开始考虑引用智能算法与优化算法对电缆控制系统进行优化,提高控制精度及适应性。

文献[7～10]在一定程度上改善了传统PID算法在多干扰、大时滞复杂非线性系统控制精度不足的缺点,但在响应时间、稳态误差性能指标上仍然有待提升。

近些年来随着机器学习、人工智能的高速发展,机器学习的应用领域普及到了各个领域。由于本文研究的电缆绝缘厚度的控制具有一定的滞后时间,本文采用对时间序列模型的函数逼近具有高精度,高效率的NARX神经网络(nonlinear auto-regressive neural network)建立电缆线径的数学模型,对传递函数进行整定,建立一个高精度的离散化传递函数,再通过PID控制器对该系统进行控制。其中PID控制器中的参数由复杂度较低的粒子群优化(particle swarm optimization,PSO)算法进行优化,由于PSO算法的使用范围对比ACO算法更好[11,12],故本文拟采用NARX-PSO-PID算法对于电缆绝缘厚度的控制进行优化。

1 电缆挤出工艺分析

绝缘挤出生产线作为电线电缆制造行业重要的生产工艺,设备组主要包括放线机构、挤出机、线径测试仪、冷却装置、牵引装置、收卷机构等。其工艺流程图如图1所示。

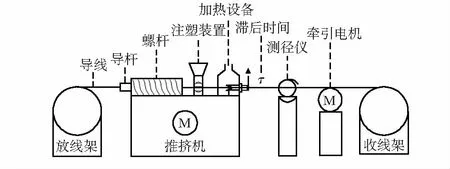
图1 绝缘挤出生产线工艺流程

根据图1所示,挤出机的工作原理是利用螺杆旋转机构,包括进料斗运送均匀的绝缘熔融材料到加热桶内,绝缘材料的熔化状态连续传输到机头模具的内部,将绝缘材料挤压成绝缘层所需的形状,挤压在导体上。绝缘挤出控制系统中的滞后问题产生的原因是测径仪一般安装在离机头较远处的位置,数据传输存在延迟。传统车间一般采用当前测得的线径值反馈给控制器,来控制当前的推挤速度,即当前的推挤速度是利用历史时刻的值进行估算,与期望值相差很大。

通过对挤出过程分析,塑料绝缘厚度由以下因素决定：1)挤出机工作区的温度和挤出机模具的温度;2)模具几何形状;3)螺杆转速;4)聚合物涂层的物理和流变特性;5)收卷驱动单元的线速。

根据上述分析可知,电缆绝缘厚度的模型建立必须考虑这5个因素,模型可由式(1)描述

δ=f{Sl,Ss,TM,μ(t),E}

(1)

式中δ为电缆的绝缘厚度,Sl为收线单元的卷线速度,Ss为螺杆速度,TM为挤出机工作区域温度和挤出机模具温度的函数,μ(t)为一个函数描述了挤出机模具的技术性能及其几何模型,E为一个常数,取决于聚合物涂层的物理和流变特性。众所周知,式(1)中的一些元素会影响挤出液的流量

Q=f{Ss,TM,μ(t),E}

(2)

将式(2)中的物理量代入塑料绝缘厚度的控制式(1)中,可得到初步模型

δ=f{Q,Sl}

(3)

考虑稳态运行条件下的质量平衡方程,可以更准确地表示上述关系,故有

Q=(πD2/4-πd2/4)Sl

(4)

式中D为挤压外径,d为电缆直径。

塑料绝缘厚度可表示为

δ=(D-d)/2

(5)

为了求解δ,可以应用二次方程的求解公式,即

(6)

当δ≪d时,可以将式(6)简化为

δ=Q/πdSl

(7)

2 算法介绍

2.1 NARX神经网络算法

NARX是一种带反馈的动态神经网络,主要用在处理时间序列问题,即能在一组时间序列中自动寻找目标变量与输入变量的函数关系。

定义Xt,yt为过程在t时刻辅助和主导变量的取值。辅助变量的上标表示变量中的具体特征,特征指过程中易测的物理变量,本文所描述的电缆系统表示挤出工作区温度、模具温度、挤出速度等,而辅助变量是由特征所组成的列向量,令其维度为m。本文中主导变量,即电缆绝缘厚度为标量

(8)

定义电缆绝缘厚度的真实际模型为f,所建立的NARX模型为,t时刻主导变量的预测值为则

(9)

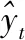
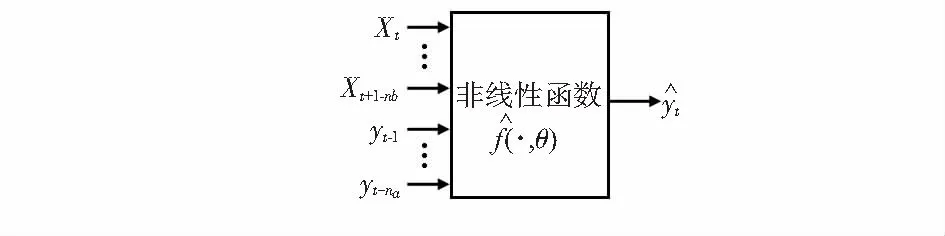
图2 NARX模型示意

2.2 PSO算法

PSO算法是一种有效的全局寻优算法,通过个体间的信息传递与竞争,寻找复杂空间的最优值。在粒子群算法中,粒子群在一个n维空间中搜索,第i个粒子在空间位置表示为xi=(xi1,xi2,…,xin),在空间中的速度表示为vi=(vi1,vi2,…,vin),通过迭代来不断校正找寻到最优解。在每次迭代过程中,粒子通过动态跟踪两个极值来更新速度和位移。其中值Pbesti=(Pi1,Pi2,…,PiD)为第i个粒子自身的最佳极值；另一个值Gbesti=(Gi1,Gi2,…,Gid)是整个种群的全局极值。确定两个最优值后,就可以建立PSO算法的位置与速度更新公式

(10)

(11)

PSO算法需要选取使控制达到最优效果的合适的适应值函数,本文选用时间乘绝对误差绝对值的积分(integral time absolute error,ITAE),即

(12)

2.3 整体算法模型

首先在理想的传递函数模型的基础上通过现场的样本数据对其修正,以获得贴近工业环境的输被控对象模型。本文以赣州某电缆制造公司车间现场所读取的数据,以及工艺流程中的传递函数完成本次实验。其中,该公司所使用的理想传递函数为

G(s)=0.6e-s/(0.9s+1)(1.5s+1)

(13)

上式为单输入单输出的传递函数,而本文在工艺分析中已提到过,电缆绝缘厚度的输出值不仅与挤出速度有关,还可能与收卷速度,模具温度等因素相关,并且由于现场环境的多样性,这些都可能使整体的传递函数出现变化。

由于电缆绝缘厚度控制系统的辅助变量较多,并且主导变量样本足够,在使用NARX神经网络对比其它神经网络具有更好的分类性以及更高的精度,故本文采用NARX神经网络对所采集的样本进行处理。将现场采集的各项数据,其中包括挤出速度、收卷速度、模具温度,代入至NARX神经网络中进行拟合,得出可能相关性大的输入与延时系数。根据上文介绍的算法,构造出整体电缆绝缘厚度系统控制的优化模型,模型流程图3所示。

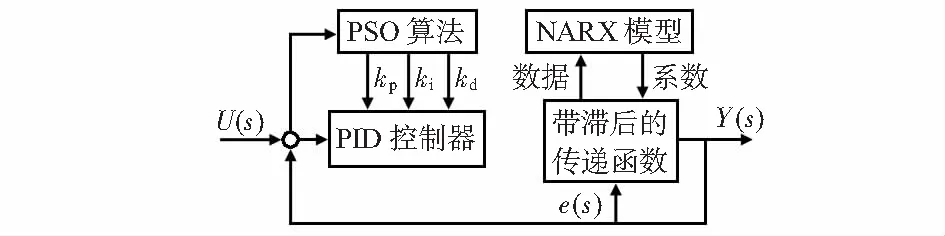
图3 整体算法模型流程图

2.4 灰关联分析法

在使用NARX比较外部变量的相关性过程中,常用输入变量选择的方法有灰关联分析法、主成分分析法、遗传算法等方法,其中,灰关联分析法简单且稳定性好。本文采用人工观察筛查结合灰关联分析法进行模型输入变量的初步选取。灰关联分析法通过计算比较序列与参考序列样本数据的灰色关联度值,判断二者之间相对变化趋势,从而确定二者之间的关联程度。常用的灰关联分析关联度有相对变化速率关联度与斜率关联度。描述事物发展过程比较合理的指标一般采用相对变化速率,若相对变化速率基本一致,则可认为2个序列有较高的相关程度。因此,本文采用灰关联分析法中的相对变化速率关联度确定输入变量。

3 实验结果与效果验证

本文采用仿真平台为MATLAB中Neural Net Time Series工具箱以及SIMULINK仿真模块。Neural Net Time Series在研究时间序列输入方面具有较强优势,可灵活选取神经网络的各项参数。

将数据集引入工具箱中进行神经网络训练与测试,以下为实验过程与仿真结果图。

根据式(1)所示,将挤出机模具的温度、螺杆转速以及收卷驱动单元的线速作为除传递函数中输入值挤出速度外的另外三个输入变量,将挤出速度标记为序号1,其余3个变量根据顺序标记为序号2,3,4。表1为输入多变量时NARX神经网络模型计算误差值以及决定系数。

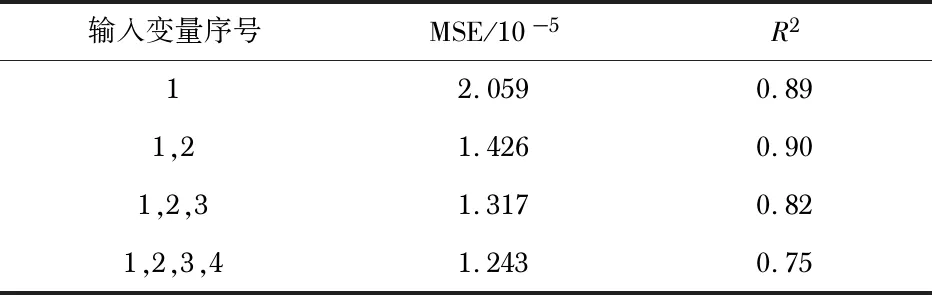
表1 输入多变量时NARX神经网络模型计算误差

表1中,R表示神经网络输出值与实际值之间的相关系数,其数学计算公式为

(14)

通过对表1分析,以及灰关联速率分析法结论,电缆绝缘厚度与模具温度还有较高的关联性,而决定系数R2也证明了该相关性。将上述确定的输入变量的结论取出,将初始传递函数数据与经NARX神经网络进行函数逼近后的传递函数数据进行对比,部分对比结果如图4所示。

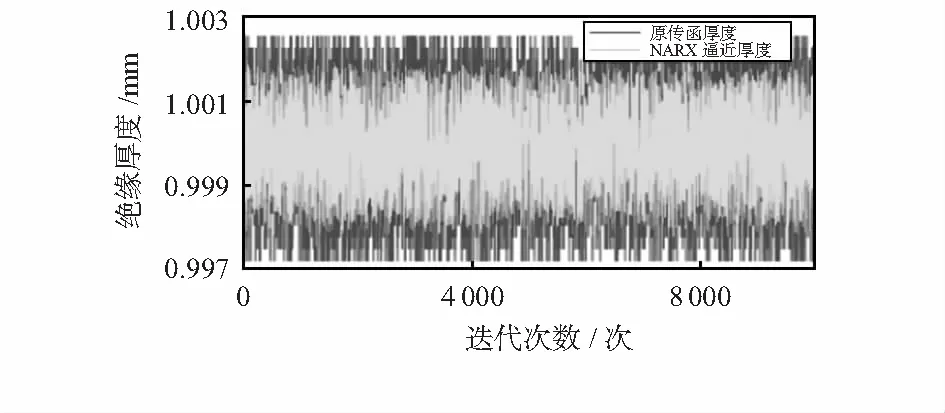
图4 原传函与新传函的电缆厚度波动对比

根据图4可直观得出,在选取上述神经网络参数后的NARX回归拟合模型对比原传递函数所得到的数据具有较高的精度与较小的噪声,所拟合的离散化传递函数更符合目标数据值,且一定程度内减小了滞后时间对于系统所造成的影响。

将由神经网络拟合的离散化模型以及适应度函数代入至SIMULINK中,调整PSO参数w=0.3,c1=1,c2=3,选取适应度函数为ITAE函数,所求得的适应值函数随迭代次数变化如图5所示。

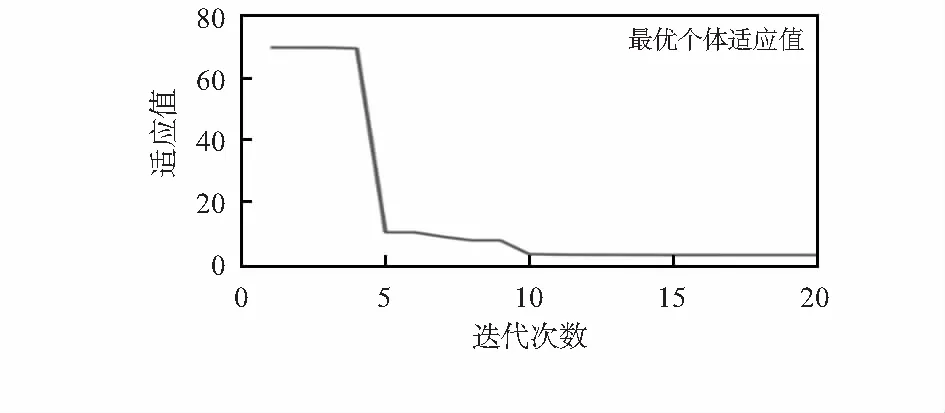
图5 适应值与迭代次数关系

由图5分析可知,PSO在第12次迭代得到了最优值,并且适应度函数值较小,另外整个优化过程局部搜索时间短,说明该算法的效率高、全局搜索能力强。

将优化好的PID参数代入至SIMULINK模块中进行仿真,仿真结果如图6所示。

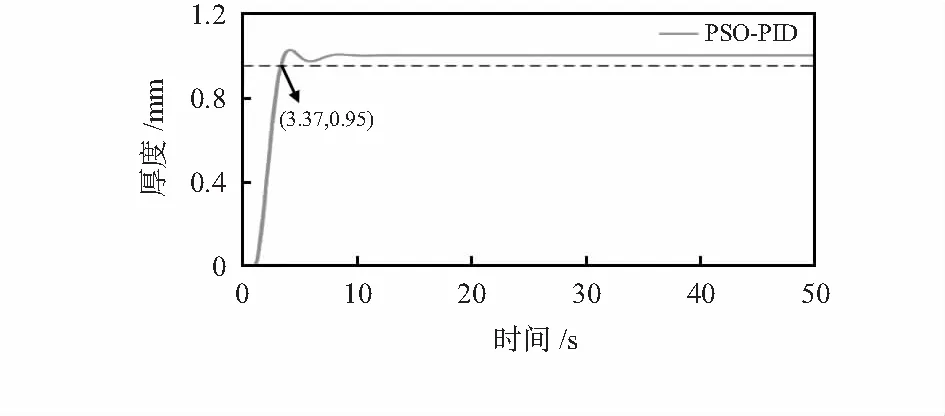
图6 PSO-PID电缆绝缘厚度—时间曲线

为了突出本文优化方法的优越性,将部分其它文献中所引用的方法引入SIMULINK模块中进行实验结果对比,实验结果如图7所示。

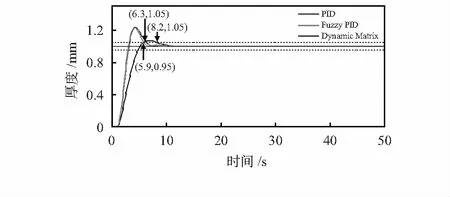
图7 其它控制算法电缆绝缘厚度—时间曲线

根据图6,图7可直观的看出,本文提出的优化算法对PID控制器以及传递函数进行优化的实验结果对比传统PID,模糊PID以及动态矩阵的方法都具有更良好的性能参数,大幅度减小了超调量,即一定程度内减小了滞后时间对系统造成的影响,完成了预测控制。并且提升了响应速度,一定程度上减小了稳态误差。

4 结 论

针对具有滞后特性的电缆绝缘挤出机,本文提出一种利用智能算法优化PID控制器的策略。在相同的滞后时间情况下,与其它文献中所提及的PID控制器、模糊PID及动态矩阵控制器进行了仿真对比实验,结果表明NARX-PSO-PID具有响应速度和收敛速度快,几乎没有超调等优点,能够高效解决电缆绝缘挤出机控制的问题,并且对类似的具有滞后性,具有可优化性的控制系统有很好的推广意义。