空间直角四面体结构磁性目标定位系统设计*
2021-03-05张晓明薛羽阳
陶 威,张晓明,张 仑,薛羽阳
(中北大学 仪器科学与动态测试教育部重点实验室,山西 太原 030051)
0 引 言
舰船及潜艇长期处于地磁场环境下,不可避免会被地磁场磁化而带有磁性[1],因此可利用这一特性对其周围空间磁场的分布信息进行检测,并对这些磁性目标进行空间定位。受磁测仪器发展的限制,基于磁场变化的磁性目标探测方法应用较少[2]。随着大量程高精度三轴磁通门技术的发展成熟,磁场张量探测逐渐成为水下磁目标探测及定位的研究热点[3]。相对于标量探测及矢量探测,基于磁偶极子模型及磁场全张量的磁性目标定位能够将异常磁场准确从地磁场分离出来,对引起磁场异常的磁目标位置三分量进行精确解算[4]。但是,现有作为磁目标定位系统硬件基础的磁场张量测量阵列多数结构复杂,传感器数量多,制造成本高昂的同时存在测量数据冗余的问题。因此设计一种简易的新型空间直角四面体结构磁性目标定位系统,这种结构的系统具有结构强度大、对称性好、造假成本低、定位精度高以及能够自矫正的优点。
1 磁性目标定位算法的建立
1.1 磁偶极子模型的建立
对于磁性目标物体而言,在其与测量阵列距离大于2.5倍自身长度的情况下,可以将其等效为磁偶极子[5],如图1所示。
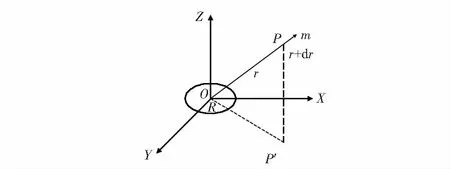
图1 磁偶极子在空间某点产生的磁场
则空间内磁偶极子产生的磁感应强度值如式(1)所示
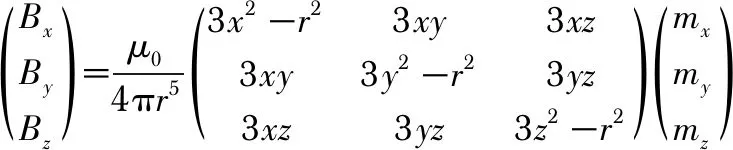
(1)
式中μ0为真空中的磁导率,H/m;r为磁性目标到探测系统中心的距离,m;x,y,z为检测点在磁偶极子坐标系中的三维坐标,m;m=[mxmymz]T为磁偶极子磁矩三分量,(A·m2)。
1.2 磁场全张量的建立
磁场全张量是由磁场三分量各自在三个方向上的分量组成的,若空间某处磁感应强度如式(2)
B=[BxByBz]T
(2)
则该点处的磁场全张量表示如式(3)
(3)
由麦克斯韦方程可知,在无源空间,磁场散度和旋度均为0,G为对称矩阵,其迹为0,即
(4)
由此可知,磁场全张量G的9个元素中只有5个是相互独立的,已知其中5个独立元素,即可对其余元素进行解算[6]。在工程应用时,多采用相邻位置磁感应强度三分量求差分的方法求取磁场全张量,当基线距离d足够小时,即可将以差分元素表示的矩阵看作是由微分元素组成的矩阵,这种方法求得近似的磁场全张量如式(5)
(5)
1.3 磁性目标定位算法
为推导磁性目标定位算法,将式(1)写成矢量形式,如式(6)所示
(6)
假设点(r+r0dr)的磁场为B′,则
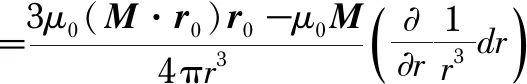
(7)
同时
(8)
联立式(7),式(8)可以得到
(9)
写成矢量形式,如式(10)
r=-3G-1B
(10)
式中B=[BxByBz]T为测量点的磁感应强度三分量,G为以测量点为基础的空间多点磁感应强度值建立的磁场全张量。
2 空间直角四面体磁性目标定位系统设计
由式(6)可知,建立磁场全张量至少需要使用8只单轴磁传感器,即只需要3只三轴磁传感器即可有效建立磁场张量测量阵列[7]。作为水下磁目标定位系统的硬件基础,现有的磁场张量测量阵列有多种构造方式,现对两种典型的磁场张量测量阵列结构进行分析,以确定磁场张量最优结构,并在此基础上进行新型磁场张量测量阵列结构的设计。
2.1 典型阵列结构分析
2.1.1 空间十单轴磁传感器阵列结构
如图2所示,空间十单轴磁传感器阵列结构采用空间立体的布排形式,6只单轴磁传感器构造2只三轴磁传感器沿X轴向前后放置,4只单轴磁传感器组成两组轴向正交的双轴传感器在Y轴向正负对称放置。

图2 空间十单轴磁力计结构
其特点是每组传感器对应连线均能通过测量点P,理论上这样可以减小因结构不对称而产生的测量误差。但在实际应用中,复杂的结构会引入大量安装误差、增大阵列体积,导致强度减小、成本增加以及无法高度集成化,因此并不适用于工程应用。因此优先考虑采用一定数量的具有良好正交性的三轴磁传感器来代替单轴磁传感器。
2.1.2 空间正六面体阵列结构
如图3所示,空间正六面体结构由7只正交分布的三轴磁传感器构成。这种结构通过原点对称布局设计实现了空间磁场梯度全张量信号的直接测量,具有提高磁场分量测量空间一致性、降低磁场梯度信号噪声的优点[8]。但是,由8只单轴磁传感器测试数据即可建立磁场全张量的分析可知,7只三轴磁传感器组成磁场张量测量阵列测试数据会出现严重的冗余,增加数据计算量的同时也增加了硬件制造成本。因此磁场张量测量阵列的设计同样需要考虑控制传感器数量。
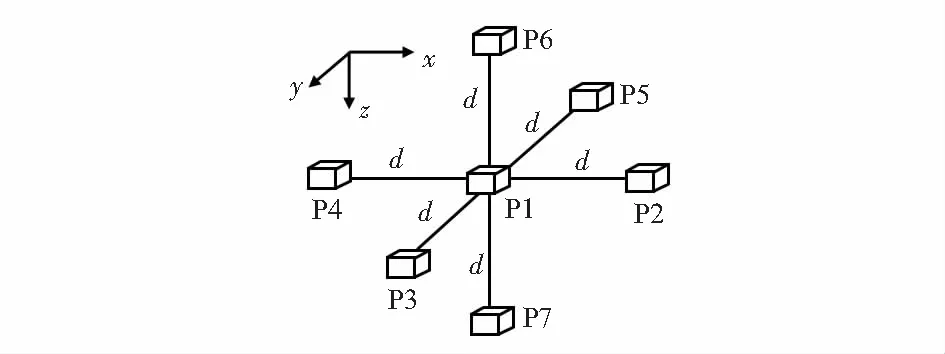
图3 空间正六面体结构
2.2 空间直角四面体阵列结构设计
综合考虑架构强度、测试精度、制造成本以及数据解算难度等因素,决定采用空间直角四面体结构磁场张量测量阵列作为磁性目标定位系统的硬件基础。空间直角四面体结构磁场张量测量阵列采用4个参数相同的某型大量程高精度水下磁通门传感器,以直角四面体顶点作为原点放置传感器S1,建立测量坐标系如图4,沿x轴正方向距离原点d处传感器为S2,且S3,S4分布同理,4只传感器量程为100 000 nT,精度可达0.1 nT,传感器使用纯铝封装,内部使用环氧树脂胶灌封,工件连接处采用O型圈密封,电缆通过高性能水密连接器接出,整个系统能承受2 MPa(相当于水下200 m处)静水压。
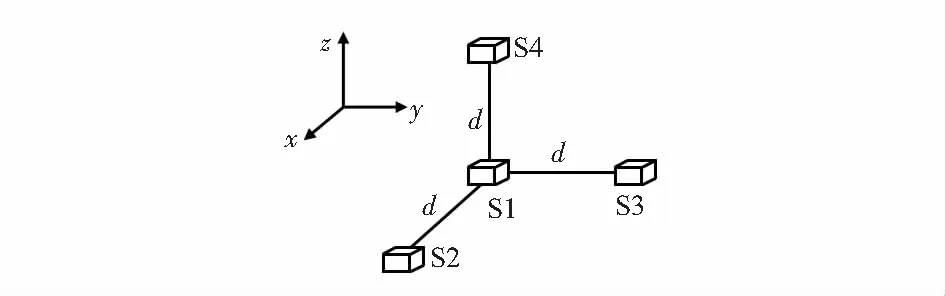
图4 空间直角四面体测量阵列结构
三轴磁通门传感器硬件集成封装后具有三轴高度正交化的优点[9],因此空间直角四面体结构仅由4只体积较小的三轴磁传感器组成。相对于空间十单轴磁传感器阵列结构,空间直角四面体结构具有安装误差小、测试精度高、适合高度集成化、强度大以及造价相对低等优点。在空间结构上,直角四面体结构相当于空间六面体结构的一半,原点处传感器S1作为参考传感器,其余3只传感器与传感器S1的连线均过阵列坐标系原点,在减少数据冗余的前提下,并不影响磁场分量测量空间一致性,即空间直角四面体结构在减小体积、降低制造成本及控制测量数据量的同时依然保有空间六面体结构的测试性能。
2.3 误差标定
理论上由大量程高精度水下磁通门传感器构造而成的磁场张量测量阵列具有可靠的测试精度,但在实际使用过程中,阵列不可避免的会出现误差,给磁目标定位精度带来影响。阵列测量误差主要分为两类:1)因制造工艺有限而造成的三轴零点、三轴灵敏度及轴间不正交角带来的制造误差[10];2)传感器安装于磁场张量测量阵列框架时存在安装误差角[11],进而给磁目标位置矢量解算精度带来安装误差。对于第一类误差,一般采用椭球拟合的方法对零点、灵敏度及轴间不正交角等9个参数进行估算并补偿。对于第二类误差,一般采用基于等效旋转思想的四位置法,建立不同姿态阵列输出之间的等量关系,对安装误差进行数学解算并补偿[12]。制造误差及安装误差补偿完毕,可认为4只传感器敏感轴向高度一致,磁场张量测量阵列输出即为准确磁场数据。到此磁场张量测量阵列结构设计完成,下一步需进行仿真验证,确定误差矫正程度及最优基线距离。
2.4 定位误差自矫正
在针对磁目标位置矢量进行反演时,不可避免存在误差,由式(5)可以看出,空间直角四面体测量阵列中S1作为参考传感器,利用磁场全张量的对称性质,联立S2,S3传感器输出构造磁场全张量。同时,将S4作为误差矫正传感器,利用S4输出数据磁场全张量精度进行矫正,如式(11)
(11)
根据磁场全张量对称性质取均值后获得的张量元素,能提高磁目标位置矢量的解算精度,在远场探测时,可以按照此原理对位置矢量反演误差进行实时矫正。
3 仿真验证
3.1 仿真实验
潜艇等水下磁目标会定期进行消磁,在一定程度上能将自身产生的特征磁场隐匿于地磁场环境下,地磁场的干扰会影响磁场张量测量阵列针对异常磁场的测量精度,给实验带来误差。因此,为排除地磁场的影响,使用MATLAB软件对基于磁偶极子模型及磁场全张量的磁性目标定位进行仿真验证,建立磁偶极子模型,验证基线距离、高斯白噪声信号及测量距离对定位精度的影响。在远距离测量的前提下,将舰船等效为一个磁偶极子,根据舰船磁矩计算模型[13],大型舰船(长180 m,宽20 m)等效磁矩计算结果如式(12)所示
mx=4×106A·m2,my=0,mz=0
(12)
磁偶极子与测量阵列相对位置如图5。阵列坐标系x轴、y轴与磁偶极子坐标系x轴、y轴方向相反,阵列坐标系z轴与磁偶极子坐标系z轴平行。磁偶极子位于相对于阵列坐标系原点(20,20,20) (单位:m)位置处。
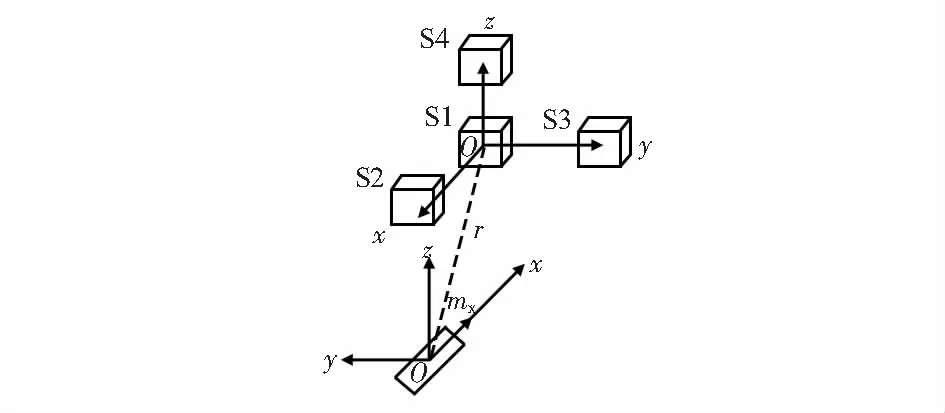
图5 磁偶极子与测量阵列相对位置
3.2 基线距离对磁性目标定位精度的影响
在基于磁偶极子模型及磁场全张量的磁性目标定位算法基础上,已知组成磁场张量测量阵列的三轴磁通门传感器精度为0.1 nT,仿真基线距离d由0.01 m变化至20 m长度过程中对定位精度的影响。仿真结果如图6(a)所示。
3.3 高斯白噪声对磁性目标定位精度的影响
磁场张量测量阵列采集空间磁感应强度数据时,信号的传输不可避免带有电路噪声。因此仿真验证磁性目标定位算法时,应加入低强度的高斯白噪声,使磁感应强度带有一定的信噪比。信噪比在10~100 dB变化时的仿真结果如图6(b)所示。

图6 基线距离、信噪比、定位距离对定位误差的影响
3.4 测量距离对定位精度的影响
在工程应用中,由于定位系统自身构造等多种因素的影响,将待测目标等效为磁偶极子的距离并不完全相同。测量距离由1 m变化至100 m时仿真结果如图6(c)所示。
3.5 运动状态下的磁性目标定位
根据仿真结果,在所用传感器精度为0.1 nT的基础上,以基线距离为1 m,添加60 dB的高斯白噪声,保持磁偶极子在相对于磁场张量测量阵列坐标系原点20 m高(即z=20 m)处在xy平面以100 m为半径绕圆一周,取90组测量点。其中,与磁矩方向呈90°夹角的两点测量点处磁场全张量为奇异矩阵,不能对磁目标位置进行反演,需对这两个点进行补偿,标准运行轨迹及位置反演散点如图7所示。
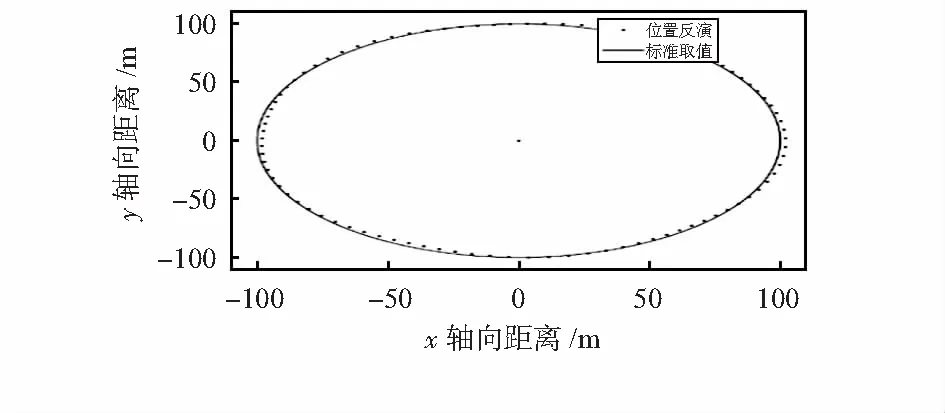
图7 磁性目标折现运动轨迹曲线
3.6 仿真验证结果分析
根据以上仿真结果分析,磁场张量测量阵列基线及测量距离对磁目标位置反演结果有明显影响。当传感器精度确定时,基线距离越小的同时测量距离越大,相对于磁场张量测量阵列而言磁目标越能有效的等效为磁偶极子,则磁目标位置反演的精度就越高。此外,一定程度上的信噪比也会带来定位误差。当信噪比提高至60 dB以上时,电路噪声对定位精度的影响较小。磁性目标在平面内作线性运动,只要能准确获得磁性目标在运动过程中到达的各个小型位置空间处磁感应强度数据,就可以对磁性目标位置进行反演,得到磁目标运动轨迹,目标在距测量点100 m处沿圆周运动,位置反演误差不超过0.5 m。综合以上分析,定位距离大于10 m时,1 m为空间直角四面体结构磁场张量测量阵列的最优基线距离。
4 试验验证
根据仿真结果设计水下磁目标定位系统实物,即4只传感器按照空间直角四面体结构排布,基线距离为1 m。将定位系统及装有磁力矩器的模型放置于平坦空旷、磁场梯度变化稳定的实验环境内,保持定位系统位置及磁目标磁矩指向东方向不变,使磁目标运动轨迹为1/4圆,如图8(a)所示。
在磁力矩器未上电前采集一组磁数据作为环境量,后续此数据均需减去环境量以得到单纯由磁力矩器产生的磁场三分量及模值。将磁测数据除以各自对应模值,进行归一化处理,根据处理的磁测数据进行磁目标位置矢量的反演并在此基础上利用张量对称的性质进行定位误差自矫正,结果如图8(b)所示。
定位误差随磁目标和阵列之间的连线与东方向夹角变化如图8(c)所示。
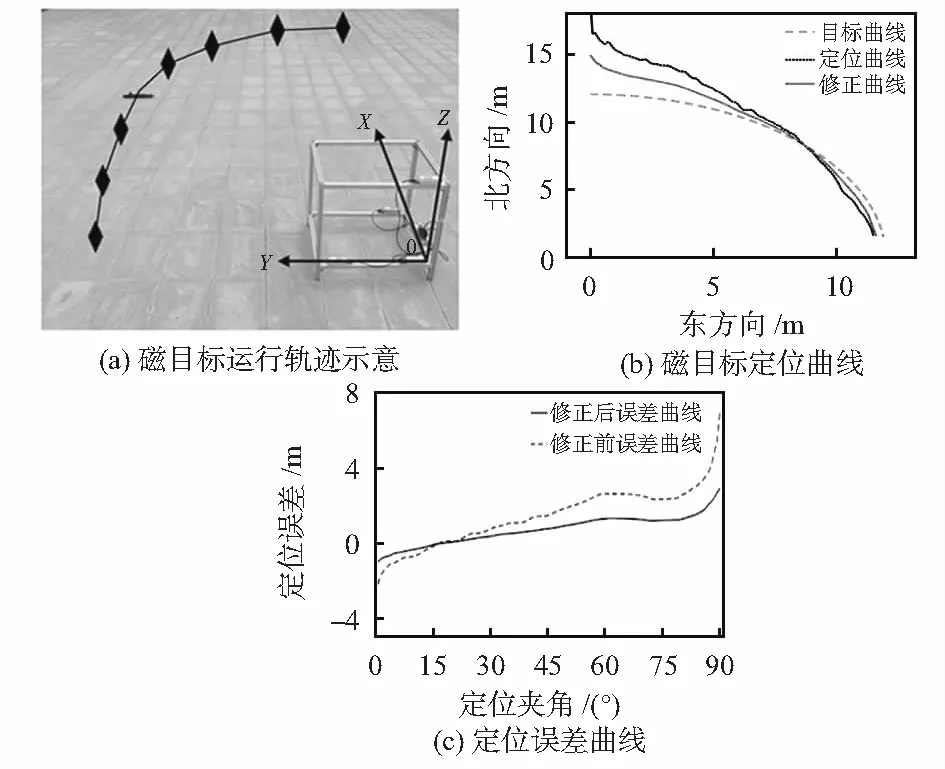
图8 试验结果
由图8(b)可知,直接构造磁场全张量对测量点位置矢量进行反演容易受测量夹角的影响。当测量夹角较小时,定位轨迹与目标轨迹相符,当测量夹角接近90°,定位轨迹发散明显,与目标轨迹相距较远。而通过系统自矫正后,整体定位轨迹与目标轨迹基本一致,证明定位系统的实用性。
由图8(c)可知,系统误差自矫正后误差显著降低,平均误差由矫正前1.142 m降低至矫正后0.699 m,精度增加了一倍,证明设计的能够自矫正的新型简易空间直角四面体结构磁目标定位系统具有较高的定位性能。
5 结束语
通过对比分析各种结构特点的磁场张量测量阵列,确定一种能够自矫正的新型简易空间直角四面体结构磁目标定位系统,通过仿真各种因素对系统定位误差的影响确定系统最优参数。试验结果表明,自矫正后的系统定位轨迹与目标轨迹基本一致,证明该系统在水下磁目标定位中具有较高的工程应用和价值。在未来,为获得更良好的定位精度,可以在如下方面进行进一步的研究:1)优化传感器结构,减小磁场张量测量阵列基线距离;2)优化定位算法,使用两点协同定位,构建目标函数,解算磁目标位置矢量。
