基于滑模观测的无感风机负载中低速控制

郑富强,韩 强

(东华大学 机械工程学院,上海 201620)

0 引 言

风机、水泵类器械是通用生产生活工具。据统计,每年风机、水泵类器械电量消耗超过发电总量的30 %,接近工业用电总量的50 %[1]。传统风机负载多采用交流异步电机变频控制,这种方法效率低、噪音大且使用寿命不长。随着对资源节约和噪音控制等要求提高,无刷直流电机(brushless DC motor,BLDCM)和永磁同步电机(permanent magnet synchronous motor,PMSM)逐渐取代交流异步电机成为风机类负载的驱动电机[2]。

无刷电机风机负载无感驱动系统的难点在于启动和速度闭环。电机启动多采用经典的三段式启动,在启动性能要求高的场合会加入初始位置检测。速度闭环控制性能主要取决于转子位置观测的准确性。这类观测算法有滑模观测、高频注入和神经网络等等。快速准确估测出转子位置信息,并及时做出控制响应是中低速运行、大惯量、非线性的风机类负载控制系统需解决的问题。

1 风机类负载与电机建模

风机[3]可定义为:用于气体输送的流体机械,它通过原动电机旋转做功推动气体流动,主要表现为改变气体压强。在一定的转速范围内,风机负载转矩输出Tl，风机风压H与风机的转速ωr的平方成正比关系,可表示成式(1),K1,K2为比例系数,取决于风机负载的具体形态

(1)

在两相静止坐标系(α,β)构建数学模型[4,5],结合电机在两相旋转坐标系(d,q)中的无刷电机电压状态方程,逆帕克变换得

(2)

式中ud,uq为(d,q)坐标系中交直轴定子电压;Ld和Lq为定子电感;id,iq为交直轴定子电流;R为定子电阻;ωe为电角速度;ψm为转子磁链。可见式(2)中电感矩阵不对称,这导致电机转子位置角信息不能完全解耦[6,7],将式(2)改写为对称矩阵并变换到(α,β)坐标系中,有电压状态方程

(3)

式中θe为电角度,令Eα和Eβ为扩展反电势,其中p为微分算子。在该模型下,扩展反电势不仅与电机的转速有关,还与定子电流id,以及iq的微分有关。电机即使运行在较低转速时,虽电机实际反电势很小,但只要有定子电流变化,仍可估测出电机实际反电势,这成为风机中低速控制应用的基础[8]。

2 滑模观测器设计

滑模控制本质上是一种非线性控制系统,它通过开关函数的不断切换实现系统结构变化,以达到系统稳定在特定状态即滑模面上的目的。这种控制的关键是滑模面和滑模增益的选取。

将式(3)变换为电流状态方程,计阻抗矩阵为A,有

(4)

(5)

(6)

sgn(x)为开关函数,设计滑模控制律

(7)

根据滑模控制三要素原理,k有限制条件

观测器中,滑模面为观测电流和实际电流差值为零的系统状态,当该条件持续满足时,即系统状态在滑模面上滑动,电流观测误差为零。此时,根据滑模控制理论,被控制量和控制量相等,即估测反电势和实际值相等,至此,扩展反电势观测完毕。通过简单的反正切计算即可得到转子位置信息,由于实际观测量为不连续的高频切换信号,需对观测的反电势信号低通滤波。这个环节会导致观测的反电势幅值和相位发生延迟。所以滤波后需附加一定的相位补偿估测角[9～11]。至此,观测器观测到了电机的转速和转子位置信息。

观测器中开关函数sgn(x)用领域Δ内线性变化的饱和函数sat(x)代替,这样滑模面被扩展为具有边界的滑模区间,对提高电机中低速运行的稳定性具有优化作用,函数表达式如式(8)所示

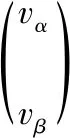
(8)

3 仿真与分析

在MATLAB/SIMULINK搭建仿真模型,电机参数根据实际电机参数设定,极对数为4,电感为70 mH,电阻为25 Ω,永磁体磁链为 0.175 Wb,直流电源输入为311 V直流电输入。设定电流环KP=17,Ki=500,速度控制环KP=1、Ki=0.2。仿真时间0.2 s,仿真模式为Ode3,定步长2×10-7s。模型如图1所示。

图1 基于滑模观测器的无刷直流无感控制仿真模型

磁场定向控制(field-orientated control,FOC)是被应用最广泛的矢量控制。该方法将电机电流状态方程变换到转子同步旋转坐标系(d,q)中。定子电流矢量分成两个分量id和iq,分别为电机产生磁通和转矩。速度反馈通过转子位置传感器获取。无位置传感器控制中位置传感器用滑模观测器代替。

风机负载的特点是大惯量、负载转矩和速度平方呈比例关系,在图1中仿真了这种关系,电机的转速ωr经平方运算后作为电机负载转矩Tl输入。根据风机负载的影响因素和风机叶片尺寸不同,此处设增益K=0.000 2。工作转速是150～450 r/min,设定目标转速为最低速150 r/min。饱和函数增益为适应低速运行环境设为K=25。

由图2(a)可见,在初始启动过程中,由于滑模结构的弊端,电机转速不稳定。但经过0.01 s,电机估测转速基本收敛到目标转速,且估计转速和电机实际转速在电机运行全状态基本保持一致。需特别说明的是本控制系统只考虑电机在速度闭环控制阶段的状态,电机启动过程通过开环加速实现,当电机达到一定速度且滑模观测器持续获得正确的位置信息后切换到本控制系统。在相对低速的150 r/min目标转速下,电机估测转速和实际转速基本相等。在电机稳定运行的0.05 s时刻将目标转速突变为155 r/min,观测突变转速时系统的稳定性。由图2(a)可见,突变目标转速短时间内电机转速有轻微超调,但整个收敛过程只用时0.01 s。

图2(b)可知,除初始阶段转子估测位置有波动以外,转子位置的估计值和实际值基本相等,0.05s时刻的突变转速也没有对转子位置估测造成任何影响。整个过程估测转速和实际转速基本保持一致,可见观测器的准确性很高,即使在突变转速的情况下也能准确的估测出转子位置。

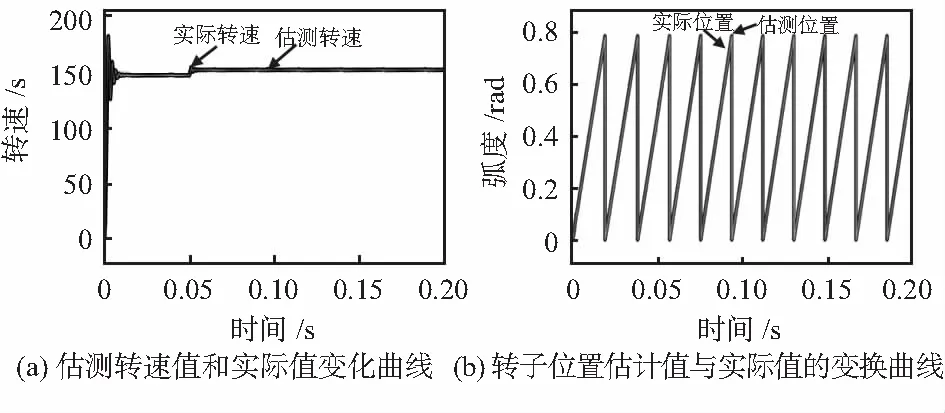
图2 仿真结果

4 实验与分析

硬件驱动板主控芯片采用意法半导体公司的STMF302C8T6芯片,以保证运算速度和存储空间的前提下减小驱动电路体积。硬件驱动板包括控制模块、电源模块、基于315MHz频率的无线遥控模块,控制信号分析的DAC模块和上位机调试的串口通信模块。驱动电路芯片采用耐500 V高压的集成高压栅极驱动芯片SD05M50DBE,电流采样选用三电阻采样,这两个模块位于驱动电路板背面。电源模块考虑到高压实时测试的需要,将交流转直流模块换成斯坦电源公司生产的可变直流电源代替,型号为AY—1500A—400,最高可输出400 V直流电源。具体硬件驱动电路板如图3所示。

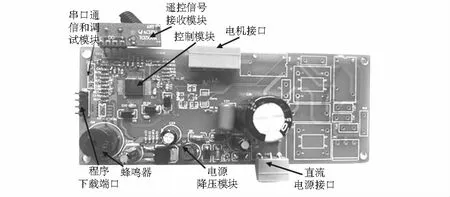
图3 电机驱动硬件电路板图

硬件驱动系统通过单片机的数模转换器(digital to analog converter,DAC)通道输出估算电机转子位置曲线图通过示波器采样如图4(a)所示。图中开始时刻是电机三段式启动过程中从开环加速切换到速度闭环时的转子位置角实测图,可见转子位置除切换瞬时的波动以外,其它时刻都非常稳定,观测器传感器估算的转子位置角连续有效。

通过图3串口接口实现与上位机在线测试。图4(b)中速度闭环时实测速度基本能以参考速度为基准,并稳定在设定速度左右。

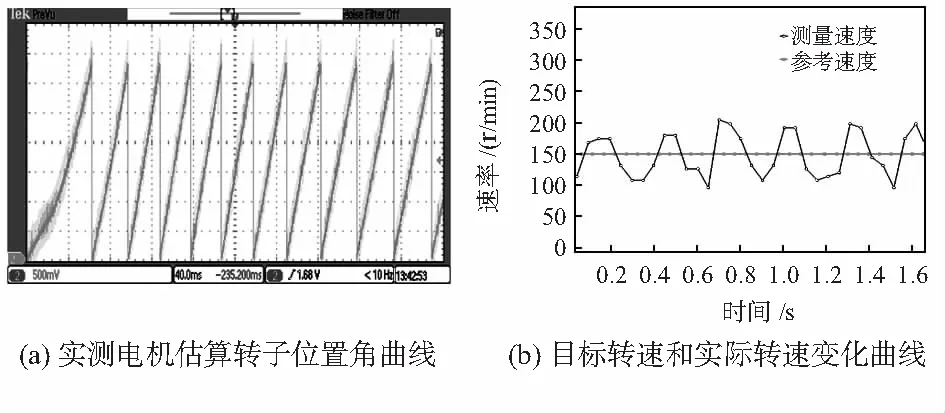
图4 实验结果

5 结 论

普通风机负载驱动电机成本低、制造精度不高、电机参数差异大,这要求控制系统对电机参数不敏感。基于饱和函数的滑模观测器控制系统具有良好的鲁棒性、中低速估测转子位置和速度信息准确、对风机类变负载响应迅速。仿真和实验可知,控制系统对无感风机负载无刷直流电机中低速能实现良好控制。