基于广义预测控制的机器人去毛刺仿真研究*
2021-03-05石益奇苏圣超
石益奇,苏圣超
(上海工程技术大学 城市轨道交通学院,上海 201620)
0 引 言
近年来,机器人去毛刺技术已逐渐取代人力成本高、生产率低的手工打磨工序。在机器人去毛刺的过程中,切削力与毛刺尺寸有关,当毛刺相对较小且分布均匀时,法向力维持恒定[1,2]。因此,控制法向磨抛力保持恒定是去毛刺的有效方法。但是,如果毛刺形状复杂多变或毛刺尺寸的突变,恒定法向力的控制策略将导致切削深度不均匀。此外,当去毛刺所需的力大于切削所需的力时,工具磨损或大毛刺引起的干扰便难以区分,从而导致末端执行器的发生偏转。在机器人精加工过程中,一般采用自适应力控制器来解决这些问题[3,4]。Jung S等人使用最小化力误差的自适应技术来补偿未知工件的不确定性[3]。Pagilla P R等人研究了法向力和切向力相关的磨削系数并通过额外的视觉传感器来获得毛刺尺寸、位置和切割深度[4~6]。Lee Y D等人提出了一种基于广义毛刺模型的快速去毛刺通道规划器,利用激光视觉传感器识别毛刺形状和倒角深度信息,但视觉传感器在环境中的芯片和灰尘的加工操作中受到限制[5]。Wiens G J等人提出了一种具有逻辑模块控制器,在毛刺的基础上修改推力,并且控制器在检测毛刺和实现期望的倒角深度方面表现良好[7,8]。最近,模糊逻辑或神经网络已被应用于控制处理高度变化的毛刺[9~11]。然而,系统地设计模糊控制器很困难,并且神经网络控制器需要学习和适应时间,受限于加工的实时控制。
本文提出了一种基于时变参数模型的广义预测控制策略。该算法对环境模型参数实现有效的估计,并利用Kelvin-Voigt机器人环境交互模型实时计算磨抛力。通过计算预测力和给定力之间的偏差值,调整机器人的磨抛深度,以获得光滑表面并减少去毛刺程序的重复次数。
1 机器人去毛刺力学模型
预测毛刺尺寸和位置是众多论文的研究方向,但毛刺的实际尺寸与位置在不同工件上存在较大的差异,图1表示常见带有毛刺工件的剖面图。
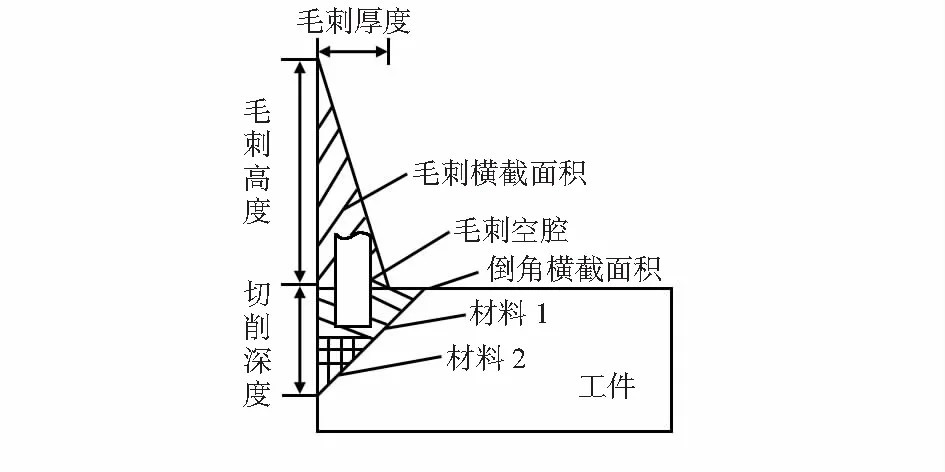
图1 带毛刺工件剖面
图中描述了毛刺的主要参数,即毛刺高度、毛刺厚度和切削深度。毛刺的平均高度为0.25~0.75 mm,厚度为0.025~0.075 mm,毛刺高度为0~1.5 mm,根部厚度为0~0.23 mm[1,12]。对于硬质合金旋转锉[2],去毛刺的平均切削力为
F=Kdf
(1)
式中F为切削力,K为切削刚度,d为切削深度,f为进给速率,切削力F可分解为平面法向和切向分量
Fn=Rn·F,Ft=Rt·F
式中Fn为法向分量,Rn为法向分量比,Ft为切向分量,Rt为切向力比。在切削过程中,毛刺的表面积切向比Rtng和法向比Rnorm可用于确定切向力和法向力的变化,因此,式 (1)可表示为
Fn=Rn·F(1+Rnorm),F1=Rt·F(1=Rtng)
(2)
根据式(1)和式(2),通过改变的倒角深度dm可以调节切削力Fr
ΔFr=Fx(dm)-Fr,Δd=dm-dr
在机器人去毛刺过程的大部分时间内,保持进给速率恒定可以获得平整的加工表面。但是,当毛刺腔体为空腔或切削材料属性发生变化时,环境参数也随之改变,切削力会发生显著变化,切削工具可能会失速或断裂。因此,需要对毛刺参数进行预测并同时改变切削力,通过这种方式,可以完全去除较大的毛刺,并且在遇到空腔时不会损坏工件。
通常,n关节约束机械手的动力学方程可以表示为
(3)
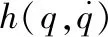
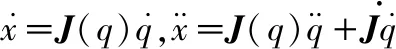
(4)
从式(3)和式(4)可以得到笛卡尔空间坐标系中的机器人动力学方程模型
(5)
其中,D*=JT-1DJ-1,h*=JT-1h-D*JJ-1x。
根据Kelvin-Voigt模型,末端执行器与环境产生的接触力特性如下
式中K,b分别为末端执行器所需的刚度和粘性矩阵。利用KV模型,接触力从零开始演化,在加载阶段达到最大值,在卸载阶段回到零。因此,KV模型符合机器人与环境之间相互作用的机理。
2 广义预测控制系统设计
本文基于Kelvin-Voigt机器人环境交互模型,设计以下广义预测控制策略框架,如图2所示。

图2 机器人广义预测控制系统
图2中Xd,d,Fd分别表示机器人末端给定位移轨迹、速度及磨抛力;J表示机器人末端执行器的雅可比矩阵;Xm,m分别表示经预测控制补偿后的位移及速度。由机器人任务规划给出笛卡尔空间坐标系机器人期望位置,通过相应的算法(逆运动学模块运算和位置控制律模块),实现期望力矩的计算,并给定到机器人模块中。此外,从机器人模块采集实时位置和末端力的反馈值,并导入到基于参数模型的广义预测算法中,并对环境参数进行预测。预测参数经过KV模型的计算,得到预测力。通过计算传感器检测到的力和预测力之间的偏差值,实现机器人的力环与位置环的控制。
由于KV利模型是线性的,其中Fe(t)可通过安装于机器人工具端上的力传感器测量,X(t),(t)可通过机器人执行器编码器测量,因此yτ=[Ke(t),Be(t)]是在线识别的模型参数。广义预测控制算法对模型要求低且具有自适应能力,能够克服模型误差和传感器测量误差,有良好的鲁棒性。在机器人打磨系统中存在着无法预知的环境变化,因此利用广义预测控制进行环境参数的预测能减小系统的误差。
广义预测控制(generalized predictive control,GPC)采用了受控自回归积分滑动平均模型
A(q-1)y(t)=B(q-1)u(t-1)+(ξ(t)/Δ)
式中u(t),y(t),ξ(t)分别为GPC控制系统的输入,输出和白噪声,j步后的对象输出y(t+j)的预测值可以采用Diophantine方程计算。在GPC中,优化性能采用最小方差优化控制,其指标函数为
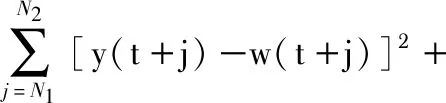
(6)
式中λj为加权系数,N1通常取1,N2为优化时域的终值。
令W=[w(t+1),w(t+2),…,w(t+n)]T,可得
u(t)=u(t-1)+gT(W-f)
式中gT为(GTG+λI)-1GT的第一行向量。为了进行柔化控制,确保在本系统设计中GPC控制输出的模型参数准确,对环境模型参数参考轨迹进行跟踪,参考轨迹如下
w(t+j)=αjy(t)+(1-αj)yτ,yτ=[Ke(t),Be(t)]
式中y(t)为输出,yτ为环境参数的测得值,α为柔化系数,取0<α<1。
上述步骤基于环境模型参数对GPC进行滚动优化,每一个局部优化目标都是在测得当前打磨实际环境参数的前提下选取最优控制信号,使预测输出结果能够良好地跟踪测量值。
3 仿真实验
对所设计的控制器进行仿真。最差的毛刺通常被认为是阶梯毛刺,工件轮廓被定义为阶梯毛刺,如图3所示。
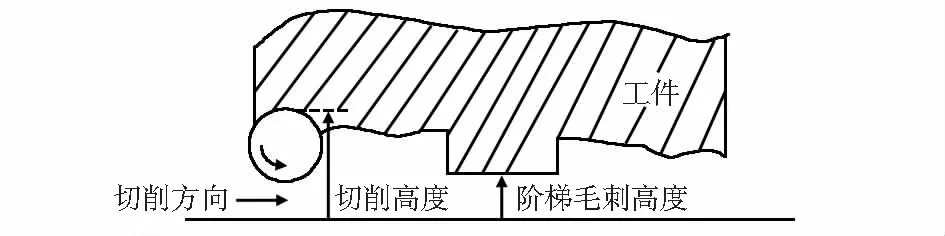
图3 阶梯毛刺工件加工示意
在该仿真环境中,地面真实环境的参数定义为时变参数。其中,K为时变周期方波信号,b为时变脉冲信号,仿真结果如图4所示。
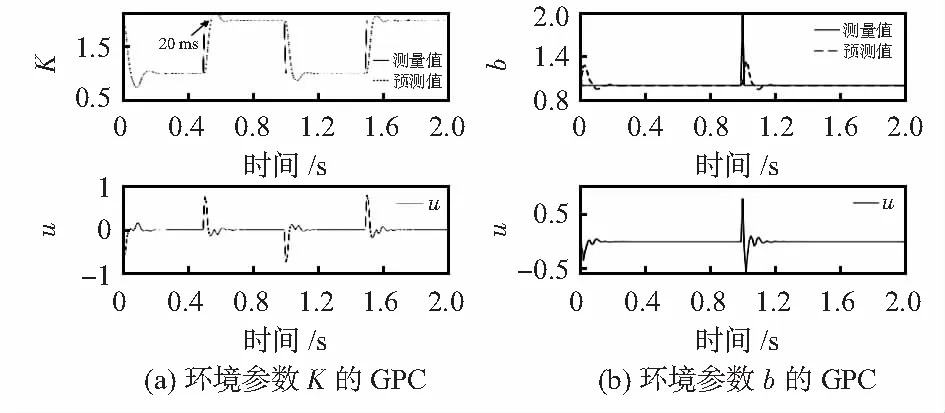
图4 GPC
在去毛刺过程中,当工具端遇到毛刺或末端材料属性发生变化时,文本采用的基于时变参数的广义预测算法,将提前20 ms左右对环境参数进行提前预估。参数估计结果经KV模型计算后,得到预测力。通过计算传感器检测到的力和预测力之间的偏差值,实现力环与位置环的控制。
图5比较了本文采用的GPC预测算法及传统阻抗算法在机器人磨抛过程中的磨抛力。传统阻抗控制的磨抛力与工件表面的形状密切相关,磨抛力之间的最大差值达到14 N左右。本文采用的预测策略,在工件表面不均匀的情况下,磨抛力最大差值仅有5 N左右。因此,本文采用的基于时变参数的广义预测控制算法对环境参数变化具有较好的鲁棒性,在机器人打磨作业中能够加工出均匀的表面,获得更好的加工质量。
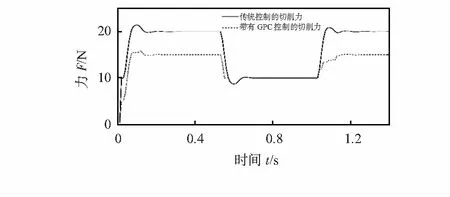
图5 GPC预测算法及传统阻抗算法的磨抛力
4 结 论
通过预测算法对环境参数进行实时预测,并反馈至Kelvin-Voigt模型预测磨抛力,计算传感器检测到的力和预测力之间的偏差值,实现力环与位置环的控制。仿真结果表明:本文提出控制策略对环境参数变化具有较好的鲁棒性,在机器人打磨作业中能够加工出均匀的表面,获得更好的加工质量。
