基于单目视觉的无人水面艇水面目标测距方法*

赵明绘，王建华，郑 翔，张山甲，张 程

(上海海事大学 航运技术与控制工程交通行业重点实验室，上海 201306)

0 引 言

无人水面艇由于其可以执行更危险的以及不适于有人船只执行的任务而吸引了广大研究人员[1]。为了实现无人水面艇的自主避障和目标跟踪等功能，无人水面艇对周围环境进行感知是十分必要的。视觉技术能切实提高无人水面艇对环境的感知能力，实现动态避障和目标跟踪等功能，增强无人水面艇对未知环境的应变能力，提高无人水面艇的航行安全。

基于单目视觉的测距问题，目前已有一些研究工作，文献[2～4]利用图像像素点、相机内参和透视投影几何关系测量前方车辆障碍物的距离。文献[5]通过视频来估计被跟踪船与相机距离;文献[6,7]利用图像中地平线与目标船之间的垂直像素距离作为测量距离;文献[8]计算垂直方向距离和水平方向距离，并且测量相机俯仰角;文献[9]分析参数误差对测距精度的影响;文献[10]分析不同相机高度、俯仰角及方向角对车距测量的影响。

本文在单目测距模型、相机高度和俯仰角标定方法的基础上，通过仿真实验分析影响测距精度的因素，通过实船实验进行验证。

1 单目测距原理

1.1 测距模型

采集水面目标图像，识别图像中目标所在区域，并计算该区域像素纵坐标最大值，及其对应的横坐标均值，将组合得到的坐标作为观测点的像素坐标。根据相机内部参数和透视投影几何关系获得观测点在相机坐标系下的深度信息，再根据刚体变换计算观测点在无人艇附体坐标系下的三维信息，进而计算观测点到艇体的距离。图1为本文采用的测距模型，可近似看成将三维场景的物体通过单个针孔相机映射成二维图像[2～5]。

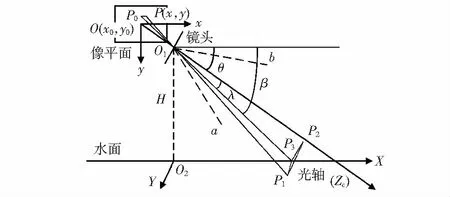
图1 测距模型

图1中，xOy是图像坐标系，Zc表示相机坐标系的Z轴及光轴，XO2Y表示无人艇附体坐标系下Z=0平面及水面，O1表示相机镜头，a,b两条虚线表示视觉场范围，θ表示相机俯仰角，观测点P1点在图像平面成像点为P，在光轴上的投影点为P2，在X轴上的投影点为P3，P3点在图像平面成像点为P0。

观测点到艇体中心的距离为

(1)

式中xs，ys为观测点在无人艇附体坐标系中Ps(xs,ys,zs)的坐标值，可根据观测点在像素坐标系下的坐标p(u,v)与在无人艇附体坐标系下的坐标Ps(xs,ys,zs)的关系求得[11]

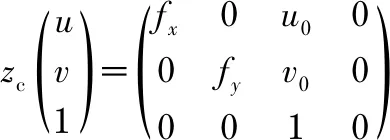
(2)

式中fx,fy,u0,v0为相机的内部参数，根据文献[12]中的方法标定而得。R为无人艇附体坐标系到相机坐标系的旋转矩阵，T为无人艇附体坐标系到相机坐标系的平移矩阵，zc为观测点在相机坐标系下Pc(xc,yc,zc)中的深度坐标值，即为距离O1P2的值

Zc=O1P2=O1P3×cosλ

(3)

其中，距离O1P3可根据几何关系得到

(4)

式中H为相机高度，λ为P0点处光线与相机光轴夹角，θ为相机俯仰角

(5)

式中y为P点在图像坐标系中的纵坐标，f为相机的焦距。在像素坐标系中，λ可表示为

(6)

式中v为P点在像素坐标系中的纵坐标，v0为图像中心的纵坐标，dy为y方向上的单位像素长度，fy为y方向上归一化焦距。

分析上述测距模型可知测距结果会受到相机高度和俯仰角的影响。为提高该方法的测距精度，需要精确标定相机高度和俯仰角。

1.2 系统标定方法

为减小在实际不确定环境中相机高度和俯仰角的测量误差对测距精度的影响，本文提出了一种相机高度和俯仰角的标定方法。

假设水面较为平静，可近似看作是一个平面。如图2所示，A(x1,y1,0)为网格坐标系下平面z=0与相机光轴(即相机坐标系的Z轴)的交点，A点在相机坐标系下的坐标为Ca(0,0,z1)。B(x2,y2,a)为网格坐标系下的平面z=0与相机光轴的交点,交点B在相机坐标系下的坐标为Cb(0,0,z2)，交点B在网格坐标系下z=0平面上的垂直投影点B′的坐标为(x2,y2,0)，则相机的俯仰角大小为∠BAB′。

图2 相机高度和相机俯仰角模型

令相机的俯仰角∠BAB′为θ，相机高度为H，θ和H可由下式计算而得

(7)

H=z1×sinθ

(8)

通过相机标定，获得与水面共面的标定板上的网格坐标系和相机坐标系的旋转矩阵R1和平移矩阵T1，且网格坐标系下的坐标XX与相机坐标系下对应坐标XXc存在如下关系

(9)

将A和Ca的坐标变量代入式(9)

(10)

即

(11)

求解式(11)可得A和Ca的坐标值。同理可以计算出B和Cb的坐标值。

2 仿真实验

分析1.1节中提到的测距模型，可知测距结果受相机高度、俯仰角和观测点像素坐标的影响。为分析相机高度、俯仰角和观测点像素坐标对测距精度的影响，建立5×5的观测物阵列作为模拟场景的观测物区域，所建场景中的无人水面艇和观测物的位置关系如图3(a)。相机的内参矩阵[3 440.9,0,623.5;0,3 440.9,551.5;0,0,1]，相机距离水面高度H=500 mm，相机与水平方向的夹角θ=5°。假设相机相对于无人水面艇的位置恒定，通过相机成像模型，将观测区域的特征点投影到无人水面艇上搭载的相机的成像平面上，如图3(b)所示。

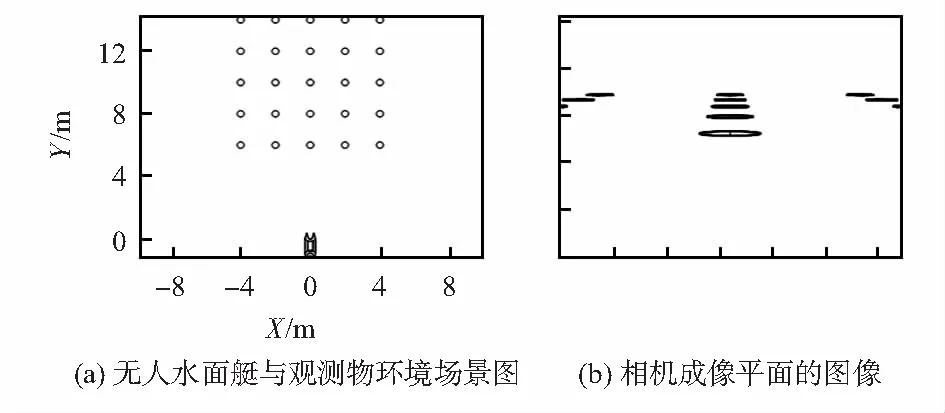
图3 仿真图

将上述方法得到的二维图像作为实际观测图像，观察相同区域的观测点，分析相机高度测量误差ΔH,俯仰角测量误差Δθ,观测点像素坐标测量误差ΔvΔu,相机高度H和俯仰角θ对测距精度的影响。

2.1 相机高度误差

ΔH为测量值H′和实际值H的差值。在观察ΔH对测距结果的影响时，设置Δθ=0，Δv=0，Δu=0，H=500 mm，θ=5°。ΔH对不同距离的测距结果的影响如图4(a)所示。分析图4(a)可知，当ΔH=20 mm时，测距结果的相对误差不随测量距离的改变而改变，当ΔH为10，-10，-20 mm时，上述规律也适用。同时，不同距离观测点的相对误差只与ΔH有关，且相对误差为ΔH和H的比值，即

(12)

2.2 相机俯仰角误差

Δθ为测量值θ′与实际值θ的差值，在观察Δθ对测距结果的影响时，设置ΔH=0，Δv=0，Δu=0，H=500 mm，θ=5° 。Δθ对不同距离的测距结果的影响如图4(b)所示。分析图4(b)可知，当Δθ=0.2°时，测距结果的相对误差随测量距离的增大而增大，当Δθ为0.1°,-0.1°和-0.2°时，上述规律也适用。当测量距离相同时，若Δθ>0，则相对误差随Δθ的减小而减小，且测距结果小于实际距离；若Δθ<0，则相对误差随|Δθ|的减小而减小，且测距结果大于实际距离；若|Δθ|相同，Δθ>0时的相对误差小于Δθ<0时的相对误差，即θ′小于θ对相对误差的影响更大。

2.3 观测点像素坐标的误差

Δv为测量值v′与实际值v的差值，在观察Δv对测距结果的影响时，设置ΔH=0，Δθ=0，Δu=0，H=500 mm，θ=5°。Δθ对不同距离的测距结果的影响如图4(c)所示。分析图4(c)可知，当Δv=2时，测量距离的相对误差随测量距离的增大而增大，当Δv为1,-1和-2时,上述规律也适用。当测量距离相同时，若Δv>0，相对误差随Δv的减小而减小，且测距结果小于实际距离；若Δv<0，相对误差随|Δv|的减小而减小，且测距结果大于实际距离；若|Δv|相同，Δv>0时的相对误差小于Δv<0时的相对误差，即v′小于v对相对误差的影响更大。

Δu为测量值u′与实际值u的差值，在观察Δu对测距结果的影响时，设置ΔH=0，Δθ=0，Δv=0，H=500 mm，θ=5°。Δu对不同距离的测距结果的影响如图4(d)所示。分析图4(d)可知，当Δu=2时，测距结果的相对误差随测量距离的增大而减小，当Δu为1,-1和-2时,上述规律也适用。当测量距离相同时，相对误差随|Δu|的减小而减小,且相对误差较小。

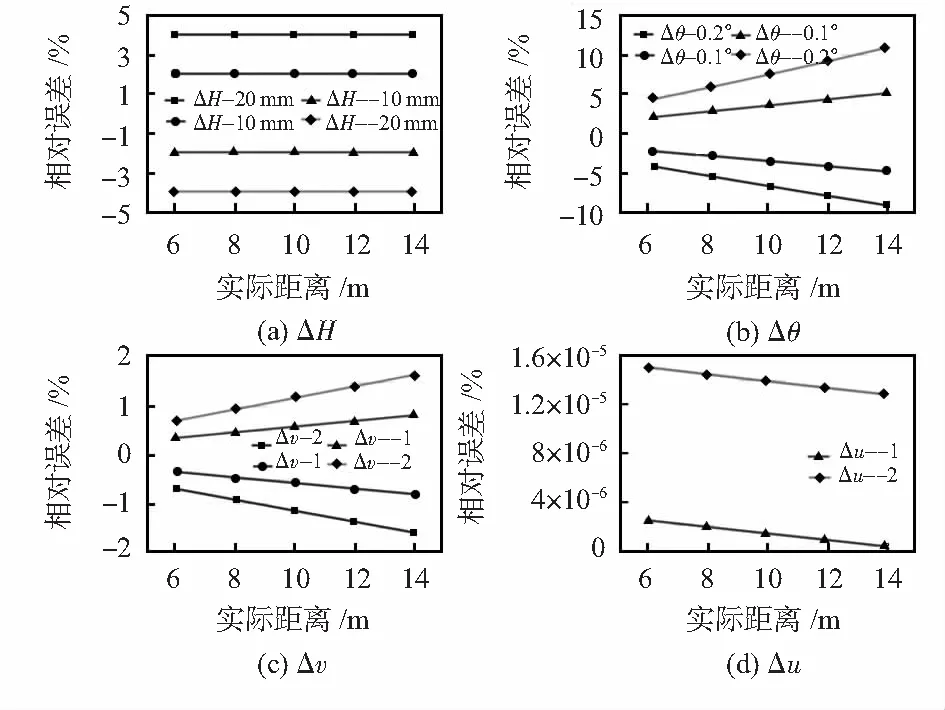
图4 测量误差对测距精度的影响

2.4 相机高度

在观察H对点测距结果的影响时，设置ΔH=20 mm，Δθ=-0.2，Δv=-2，θ=6°，观察H为600，900，1 200，1 500 mm时对不同距离观测点的测距结果的影响如图5(a)～(c)所示。分析图5(a)～(c)可知，当ΔH、Δθ或Δv不为0时，测距结果的相对误差随H的增大而减小。

2.5 相机俯仰角

在观察θ对测距结果的影响时，设置ΔH=20 mm，Δθ=-0.2，Δv=-2，H=900 mm，观察θ为6°，8°，10°，12°时对不同距离观测点测距结果的影响如图5(d)～(f)所示。

分析图5(d)～(f)可知，当ΔH,Δθ或Δv不为0时,测距结果的相对误差受θ影响较小。

图5 相机高度和俯仰角对测距精度的影响

3 实船实验

将本文提出的测距方法应用于无人水面艇进行水面目标测距。如图6(a)所示，将相机固定到“海博”号无人水面艇上。图6(b)是实验场景图。

图6 实验平台

采集的单帧图像如图7(a)所示，提取水面目标的所在区域[12]，计算出该区域像素坐标纵坐标最大值，及其对应的横坐标的平均值，将组合得到的坐标作为观测点的像素坐标，如图7(b)所示，计算该观测点到无人水面艇的距离。

图7 水面目标图像和观测点提取

由仿真实验可知相机俯仰角的大小对相同区域观测点的影响可忽略，通过调整相机高度和俯仰角采集相同区域的图像，分析相机高度对测距精度的影响，见表1。

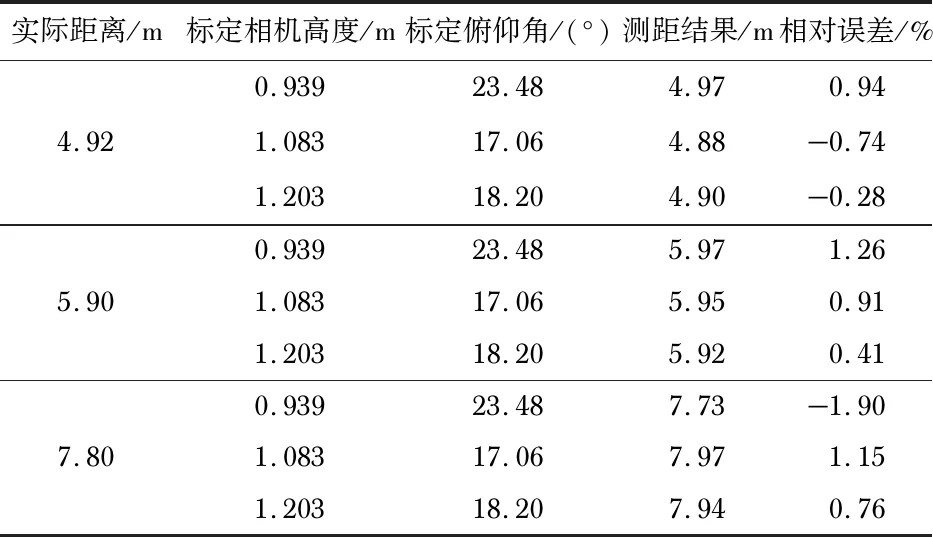
表1 不同相机高度对测距结果的影响

用本文提出的标定相机高度和相机俯仰角的方法对相机高度和俯仰角进行标定，标定结果见表1。表1中的实际距离由雷达测得，通过实验进一步验证相对误差随相机高度的增加而减小，随测量距离的增大而增大。

4 结束语

本文提出一种相机高度和俯仰角的标定方法和一种水面目标的单目测距方法。仿真实验表明:采集相同区域的图像，当相机高度和俯仰角相同时，相机俯仰角测量误差是影响测距精度的主要因素；当相机高度和俯仰角不同时，相机高度是影响测距精度的主要因素；测量距离越近，测距精度越高。实船实验表明：本文提出的单目测距方法在测量距离10 m以内目标时的相对误差小于3 %，可应用于低速无人艇的避障和目标跟踪。