温度影响下基于协整的频率修正研究

黄 然

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引 言

近年来,桥梁健康检测技术愈发成熟和完善,基于动力的结构健康监测是目前研究最为广泛的一个方向,桥梁结构的动力参数是桥梁健康监测的一个重要指标,结构动力参数识别是基于结构动态测试的模态分析方法,模态参数(通常是模态频率)反映了结构的健康状态信息。通过研究桥梁模态参数的改变来对桥梁健康状态进行监测和量化评估,是进行桥梁健康监测的基本思路[2]。

先前的研究表明温度是影响模态参数尤其是模态频率的最主要因素,主要原因有:① 温度可以直接影响材料的弹性模量,而通常f～E1/2;② 温度变化可以影响结构的边界条件,例如冬季基础冻结会提高结构的整体刚度;③ 温度的变化在超静定结构会产生温度应力,应力的改变进而会引起频率的改变。例如,Alampalli[3]通过对一小桥研究表明,由于温度下降边界支座冻结导致的桥梁固有频率的变化(变化幅度为=40%～50%)比人为造成损坏而导致频率变化(变化幅度为=3%～8%)大了一个数量级。Askegaard等[4]发现,一座3跨人行桥的正常频率在一年中变化10%。

因此,在实际桥梁结构健康监测中环境因素的影响不可忽视,如何从健康监测系统中分离出温度因素的影响一直是健康监测领域研究的热点和难点。因此,本文引入计量学中的协整理论,它在健康监测系统中分离这些无害的环境变化被证明具有巨大的潜力。

1 协整理论

1.1 概述

Cross[5]最先提出将计量学中的协整理论应用到结构健康监测领域,并且详细分析协整为何可被应用到结构健康监测中。这里首先介绍单整的定义,如果一个序列经过一次差分后变成平稳的,就称该序列是一阶单整序列,记为I(1)。一般地,如果一个时间序列经过d次差分后变成平稳序列,则称原序列是d阶单整序列,记为I(d)。

而协整的定义最早是由Engle和Granger[6]给出的:

由n组的d阶单整序列组成的向量yt=[y1t,y2t,…,ynt]′,如果存在一个向量β=[β1,β2,…,βn]′使得线性组合βyt=β1y1t+β2y2t,…,+βnynt是一个d-b阶单整,其中b>0。则向量yt=[y1t,y2t,…,ynt]′称为d、b阶协整,记为yt～CI(d,b),向量β称为协整向量。

1.2 ADF检验

协整是分析非平稳序列的一种工具,在应用协整之前需要对序列进行平稳性判断,确定序列的单整阶数,这里采用ADF检验。ADF检验是在Dickey和Fuller[7,8]提出的DF检验基础上扩展形成的。对于一个p阶自回归模型AR(p):

yt=α1yt-1+α2yt-2+…+αpyt-p+ut

(1)

对式(1)进行差分和整理得:

Δyt=δyt-1+η1Δyt-1+…+ηp-1Δyt-p+1+ut

(2)

式中:δ=α1+α2+…+αp-1;ηi=-(αi+1+…+αp);ut是白噪声。

当δ=0时,即α1+α2+…+αp=1,此时式(2)作为一个线性差分方程,其对应的特征方程λp-α1λp-1-α2λp-2-…-αp=0必存在一个单位根,因为λ=1是该特征方程的一个解,1-α1-α2-…-αp=0。ADF检验的原假设和备用假设是H0∶δ=0和H1∶δ<0。

确定了各个变量的单整阶数后,在满足协整前提下就可以使用Johansen程序对多个序列之间是否存在协整向量进行检验。

1.3 Johansen协整检验

Johansen[8,9]给出了一种基于矩阵的秩和特征根的协整检验方法,称为Johansen协整检验。考虑不包含截距项的n维p阶VAR模型:

Yt=A1Yt-1+A2Yt-2+…+ApYt-p+et

(4)

对上式(4)进行变形整理可以得到:

(5)

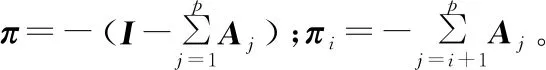
在满足r(π)=r的条件下,最大化样本数据[y1t,y2t,…,ynt]′的对数似然函数。为此,须先确定协整秩r。当协整秩为r时,系数矩阵π有r个自由(线性无关)的行向量。当协整秩r越大,对矩阵π的约束越少,对应的似然函数最大值应该越大。

据此进行似然比检验,由于检验统计量涉及矩阵的迹(主对角线元素之和),故称为“迹统计量”(trace statistics),记为λtrace。

“迹检验”(trace test)是似然比检验,为单边右侧检验,为单边右侧检验,即λtrace越大,则越倾向于拒绝原假设。

故首先进行以下检验:

H0∶r(π)=0vsH1∶r(π)>0

原假设为协整秩为0,不存在协整关系;替代假设为协整秩大于0,存在协整关系。如果接受原假设H0∶r(π)=0,则认为不存在协整关系。反之,继续检验是否存在多个协整关系,其对应的原假设和备选假设为:

H0∶r(π)=1vsH1∶r(π)>1

如果依旧拒绝原假设,则依次顺序不断进行以下检验：

H0:r(π)=2vsH1:r(π)>2

⋮

H0:r(π)=rvsH1:r(π)>r

直到接受原假设,确认协整秩r为止,即序列之间存在r个协整向量。

2 试验模型监测数据的采集和处理

2.1 试验模型

为了深入研究协整算法在消除环境温度的影响,本文以一个长3 m两端固结的钢梁为研究对象,梁两端各使用4个高强螺栓固定在支座上,每个支座通过2个地锚固定在预留在地面的槽中。试验将整个梁划分15等份,共布置14个加速度传感器用以采集梁体的振动信号,加速度采样频率为500 Hz。除此之外,还在梁上布置3个温度传感器用以记录试验过程中梁体的温度变化,加速度的布置和激振器布置如图1所示。

图1 加速度传感器和温度传感器布置

2.2 试验数据的采集和数据处理

为了得到梁的频率随温度变化的关系,分别对梁进行升温和降温两种操作,在温度变化的过程中对梁使用激振器进行脉冲激励,温度变化过程中使用高精度的加速度传感器采集梁体的振动信号、使用温度传感器采集梁体的温度变化。对采集的加速度数据进行模态参数识别。

梁在无损状态下前4阶频率的时间序列的曲线图如图2所示。

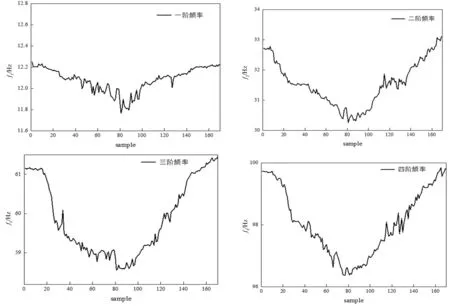
图2 前4阶模态频率识别值变化曲线图

从图2中可以看出,一方面结构的前4阶频率的变化趋势和温度变化呈相反的趋势,随着温度的升高结构的频率逐渐降低,另一方面各阶频率随着温度变化都呈现出相同的趋势。

2.3 基于协整消除温度对结构频率的影响

在进行Johansen协整检验之前,第一步需求被检验变量是同阶单整的,分别对这4个频率序列进行ADF单位根检验,检验的结果见表1。

表1 结构前4阶频率以及差分项ADF单位根检验结果

由表1可以看出,结构的前4阶频率均不能拒绝单位根的原假设,其一阶差分项在5%的显著性水平下均拒绝原假设,表明这4个频率序列均为一阶单整,即满足Johansen协整的前提条件。图3描绘了各阶频率之间的关系,从图3中可以看出,f1,f2和f4之间有比较明显的线性关系,而f3与其他各阶频率之间没有明显的线性关系[10],这也进一步显示了各阶频率序列之间可能会存在某种线性组合。在确定Johansen协整检验的方程特征时,协整方程存在截距项,没有趋势项,这4个变量的检验的结果见表2。

图3 各阶频率之间关系散点图

表2 Jonhansen检验结果

由检验结果可知,4阶频率之间存在且只存在唯一的协整关系,通过计算可以得到标准化的协整向量为[1,-0.1813,-0.1713, 0.3670,-7.9295],因此,各个频率序列之间的协整方程可以表示为:

f1+0.1813f2+0.1713f3-0.3670f4+7.9295=0

将结构的前4阶频率利用上面的协整方程计算出协整余量序列，如图4所示。图4中上下两条控制线为协整余量的均值±3标准差,根据协整理论可知,如果两个或多个变量是协整的,那么它们的线性组合是原始数据集中共同趋势的一个固定残差。就结构健康监测所测的参数而言,它所消除的共同趋势就是环境和运营条件的改变,在本例中消除的就是温度因素。

图4 协整余量曲线

3 结 论

(1) 结构在无损状态下,随着环境温度的升高,结构的频率逐渐降低,且多阶频率在温度的变化下都呈现共同的趋势。

(2) 通过协整分析可知,结构的前4阶频率之间存在协整关系,通过线性组合得到一个消除多个变量共同趋势的平稳残差，并且残差序列在一定的范围内波动，可以通过序列是否偏离控制线来判断结构的状态。

(3) 与其他消除环境因素的方法相比,协整具有以下优势:① 原理简单,理论明确;②不需要对原始序列进行处理,保留了序列的原始特性。