日本九州俯冲带b 值成像及其构造意义*
2021-03-05李云杰周鹏翔夏少红万奎元孙金龙
李云杰 , 周鹏翔 , 夏少红 , 万奎元 , 孙金龙
1. 中国科学院边缘海与大洋地质重点实验室, 南海海洋研究所, 南海生态环境工程创新研究院, 广东 广州 510301;
2. 中国科学院大学, 北京 100049;
3. 南方海洋科学与工程广东省实验室(广州), 广东 广州 511458
日本九州俯冲带是太平洋板块与欧亚板块俯冲汇聚边界上一个独具构造特色的区域。其特点主要表现在三个方面: 1) 海脊俯冲: 作为太平洋板块向菲律宾海板块下方俯冲后撤形成的残留弧(Okino et al, 1994; Pownall et al, 2017), 九州-帕劳海脊沿NW 方向俯冲于欧亚板块之下; 2) 不同时代的洋壳在此同时俯冲: 九州-帕劳海脊分隔了其东北侧的四国海盆洋壳和西南侧的西菲律宾海盆洋壳(图1a), 两者分别形成于不同的时代(Hilde et al, 1984), 但都以2~8cm·a–1的速度与九州-帕劳海脊一起朝NW 方向俯冲(Mahony et al, 2011; Yokota et al, 2016); 3) 三者俯冲后在深部的形态各异: 研究显示, 三者在进入俯冲带深处后, 海脊两侧的俯冲板片倾角显著不同, 出现了沿海脊走向的板片撕裂(Mahony et al, 2011; Cao et al, 2014; Nakajima, 2019)。这些构造特征使得该区域成为俯冲带研究的理想场所, 引起了众多学者的关注。
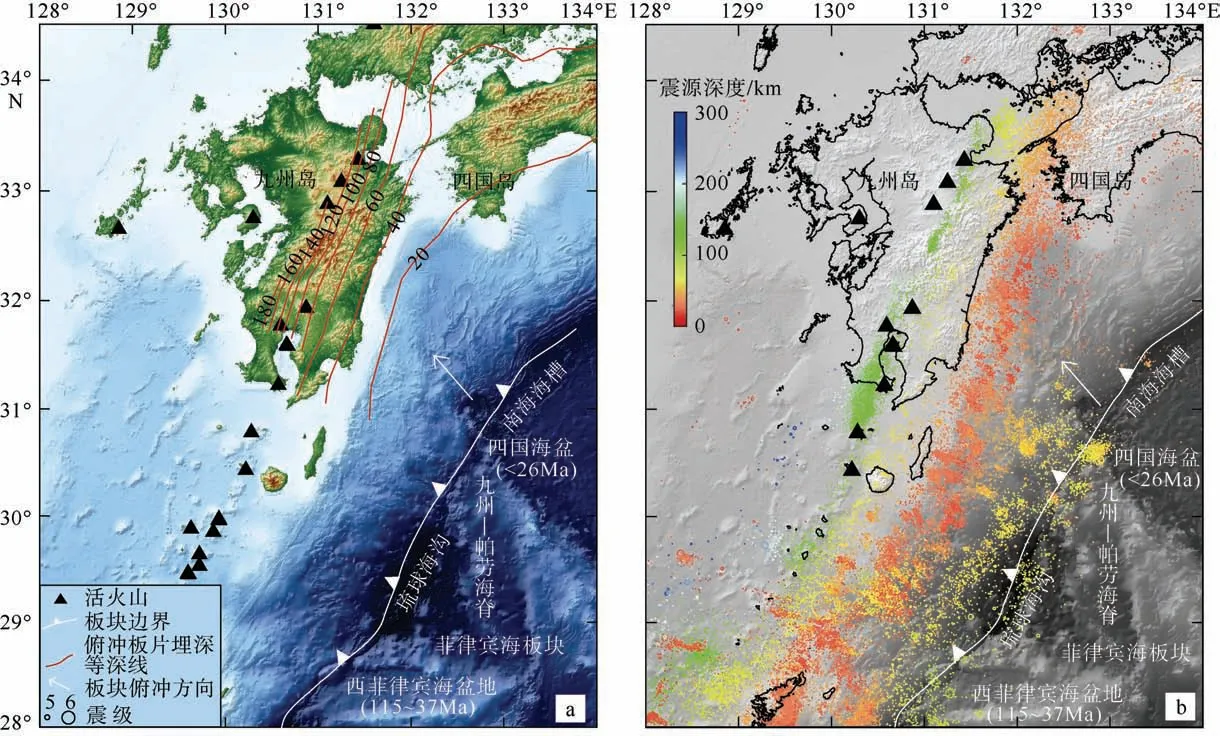
图1 研究区地形与构造概况图(a)和本研究使用的地震震源分布图(b) 俯冲的菲律宾海板块上边界埋深等深线在图a 中用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004); 图b 中彩色圆圈/点为地震震源分布, 大小均以震级乘以同个系数成图, 图例中只列出5 级和6 级作为地震大小参考 Fig.1 (a) Overview of the tectonic of the study region. (b) Distribution map of seismic source locations (colored circles/dots) used in this study
前人在这一区域虽然开展了许多有关深部结构、板块汇聚速度、地球化学、重磁异常等方面的研究(Nakajima et al, 2007; Park et al, 2009; Zhao et al, 2012; Yokota et al, 2016), 但在揭示俯冲带深部的板块作用特征上仍然存在一些不足。比如, 地震层析成像等研究虽然展现了俯冲带中上部的结构特征, 但无法反映俯冲带内汇聚板片之间的耦合作用; 基于GPS 观测的运动学研究虽然揭示了该区的板块汇聚特点, 但是由于观测台站主要位于地表, 对于了解俯冲带深部的应力状态十分有限。
鉴于上述情况, 本文尝试利用地震b 值分析该俯冲带内的应力特征。b 值表征了大、小地震之间的比例关系, 是检查一个区域内地震活动的最有效的方法之一。此外, 已有研究表明, b 值与差应力之间存在负相关关系, 在一定范围内可作为“应力指示计” (Scholz, 1968; Schorlemmer et al, 2005; Rivière et al, 2018)。值得一提的是, 研究区密集的地震观测台网积累的海量数据为本研究提供了充分的条件。为此, 本文通过计算俯冲板片上表面以及垂直剖面的b 值, 分析其空间分布特征, 并在此基础上探讨板块应力特征及板块相互作用特点。
1 数据和方法
1.1 数据
本次研究收集了日本气象厅(http://www.data. jma.go.jp/svd/eqev/data/bulletin/eqdoc_e.html)2008年1 月1 日至2017 年12 月31 日期间共388575 个地震的数据资料, 震级(Mj)分布介于–1.4~7.3 级。Mj是日本气象厅使用的震级标度, 表示基于地震波振幅的震级。前人使用同一组具有不同震级标度(Mj和Mw)的地震数据分别计算b 值, 两种震级标度得到的b 值具有很好的相关性, 表明使用Mj震级标度的地震数据计算b 值是可行的(Uchide et al, 2018)。
本文主要选取了研究区内震源深度介于20~300km 之间的地震, 原因有三个: 1) 震源深度小20km 的地震包含了上覆板块的板内地震和板间地震, 需要区分不同类型的地震才能准确分析俯冲板块对地震的影响; 2) 远离海岸的地震定位精度低, 震源深度往往被人为定义为大于20km(Nanjo et al, 2018); 3) 深度大于300km 后几乎没有地震。经过这一筛选, 符合条件的地震有 97251 个, 震级介于–0.6~6.8 级之间。
1.2 最小完整性震级
最小完整性震级(MC)是指在一定时空范围内, 台网能记录到的最小地震震级(Zhou et al, 2018), 是表征台网监测能力的最重要的物理量。通常MC值越小数据分辨率越高, MC值越大数据分辨率越小(Rodríguez-Pérez et al, 2018)。相关测试计算表明, MC的微小变化可以影响相当比例的相关地震数目(韩立波 等, 2012)。因此, 为客观揭示特定时空范围内的地震活动规律, 必须对MC进行科学、准确的评估。
目前用来估算MC的方法有两种(Wiemer et al, 2000): 基于地震目录和基于波形数据。其中, 后者方法耗时, 且通用性差。相比之下, 前者方法简单有效, 且有多种流行算法(Woessner et al, 2005)可供选用。
本文采用最大曲率法(Maximum Curvature- method, MAXC)(Wiemer et al, 2000)计算最小完整性震级(MC), 该算法把震级-频度曲线的一阶导数最大值所对应的震级作为最小完整性震级。与其他算法相比, MAXC 方法计算得到的MC(MAXC)最小, 再加上校正值0.2, 即MC=MC(MAXC)+0.2(Woessner et al, 2005), 即可得到该区的最小完整性震级。经计算, 研究区震源深度大于20km 的地震平均MC值为1.2。由于整个研究区的MC值变化幅度较大(介于0.2~2.8之间), 为了提高每个节点的b 值的准确度, 本文对每个网格节点中的MC进行单独计算, 最终得到的MC值分布特征如图2 所示。
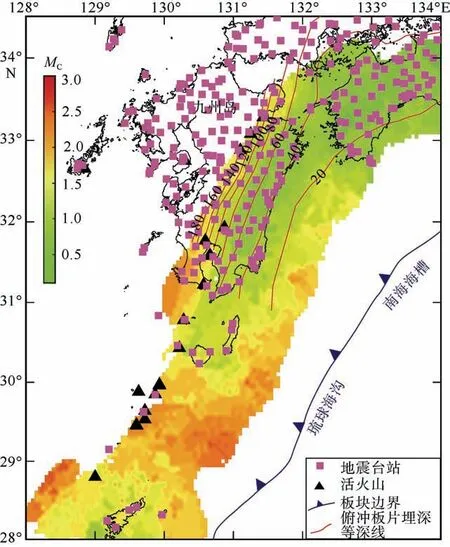
图2 最小完整性震级(MC)的分布特征 俯冲的菲律宾海板块上边界埋深等深线用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004) Fig.2 Distribution of Magnitude of Completeness (MC). Depth contours of the upper boundary of the subducting Philippine Sea slab are shown in red with an interval of 20 km (Wang et al, 2004)
根据图2 所示, 九州东部陆地区域MC值范围主要在0.5~1 之间, 少部分在1~1.5 之间; 受观测台站位置所限, 海上区域MC值基本都大于1.5, 表明该区的地震目录有足够样本, 能够为b 值分析提供较高的分辨率。
1.3 b 值计算
研究表明, 地震的震级-频度关系在较大范围内能够满足古登堡-里克特(G-R)关系(Gutenberg et al, 1944):

式中: N 是大于或等于震级M 的地震累积数; a 和b为常数, 其中b 是对数线性关系的斜率, 称为b 值。
计算b 值的主要方法有两种: 最小二乘法和极大似然法(Aki, 1965; Utsu, 1966; Shi et al, 1982)。虽然两种方法计算的结果都会随着样本数量的增加而逐渐趋于一致(张建中 等, 1981), 但极大似然法更为简单, 具有更好的抗误差能力, 结果更接近于真值, 得到的均方误差最小(张建中 等, 1981; 刘雁冰 等, 2017; Nanjo et al, 2018; Chiba, 2019), 也是目前使用最为广泛的方法(Srivastava et al, 2015)。因此, 本文选取极大似然法来进行b 值的拟合估算。
Aki(1965)最早在式(1)的基础上引入了最大似然法估算b 值, 随后Utsu(1966)进行了改进, 其计 算公式为:
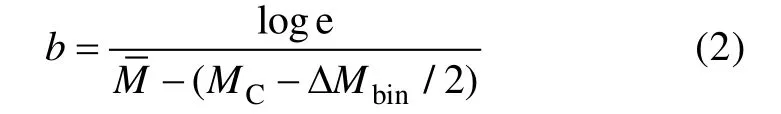
对于b 值的不确定度, 本文使用下面公式来估算b 值的标准差δb(Shi et al, 1982):
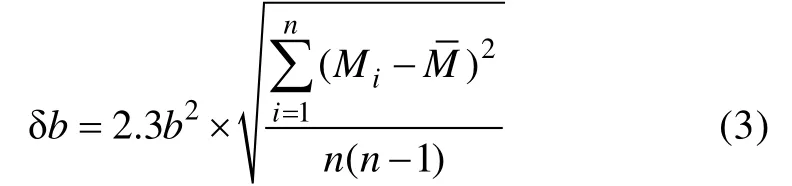
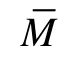
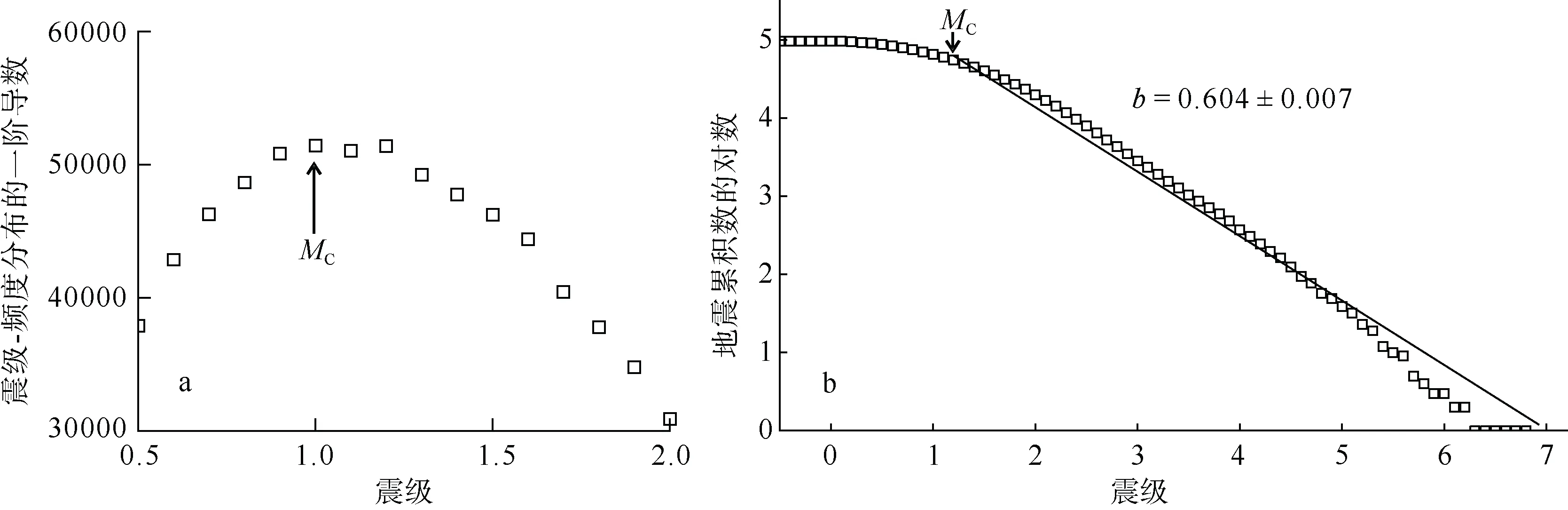
图3 研究区域地震震级-频度分布 图b 中黑色线表示在MC=1.2 下的极大似然法拟合回归线 Fig.3 Frequency-magnitude distribution of earthquakes in the study area. The light grey line in (b) denotes the maximum likelih ood fitted regression line at MC=1.2
为了得到不同节点的准确b 值, 本文开发了类似于ZMAP 算法(Wiemer, 2001)的代码来完成计算。该代码可以自定义最大采样半径和最小采样地震数, 通过限制扫描半径输出计算结果。扫描半径的改变只会影响b 值的覆盖范围, 而不会导致b 值平滑, 同时兼顾了计算结果的准确性和覆盖范围, 因此在确保b 值计算结果准确度的同时也保证了b 值的稳定性。前人研究表明, 在使用极大似然法估算区域整体b 值时, 当有效地震数量大于或等于50 时, b 值趋于稳定, 即b 值不会随着地震数量的增加而出现较大变化(Marzocchi et al, 2003)。因此, 在实际计算中, 本文采用最近距离-固定事件扫描方法, 代码运算逻辑设定为: 1) 以空间网格节点为圆心, 在半径为1km 的球体范围内筛选和统计地震事件集; 2) 根据筛选得到的地震事件集计算MC; 3) 判断地震事件集中震级M≥MC的地震数量n 是否大于或等于50; 4) 如果n≥50, 则取该MC计算该半径下网格节点的b 值; 5) 否则以2km 的滑动步长增加半径, 重复上述1~4 步, 直到球体范围内震级M≥MC的地震数量达到50 或以上后, 再进行b 值计算。如果半径增加到35km 后, 震级M≥MC的地震数量还未达到50, 则放弃该网格节点的b 值计算。同时, 为了使每个网格节点估算的b 值更接近于真实的b 值, 代码限定每个网格节点25km 半径范围内至少有1 个地震。在同时兼顾b 值分辨率和覆盖范围的前提下, 经过反复计算, 最终得到了两组b 值计算的最优参数。
其中, 第一组用于计算菲律宾海板块上表面的b 值分布: 以最新的全球俯冲带三维几何模型(Slab2)中的菲律宾海板片三维几何模型作为空间网格[网格间距约5km(Hayes et al, 2018)], 以空间网格节点为圆心, 在以最小半径为1km、最大半径为35km 的球体范围内从小到大依次对地震进行筛选和统计, 获得地震事件集N1; 根据地震事件集N1计算相应的MC, 滑动步长为2km; 要求每个节点球体内震级M≥MC的地震数不少于50 个(Marzocchi et al, 2003; Nanjo et al, 2018), 且以网格节点为圆心, 半径为25km 的球体范围内至少有1 个地震事件。此组参数最终计算得到的扫描半径和b 值的标准误差如图4 所示。由图可知, 研究区内地震事件丰富, 计算结果可靠。
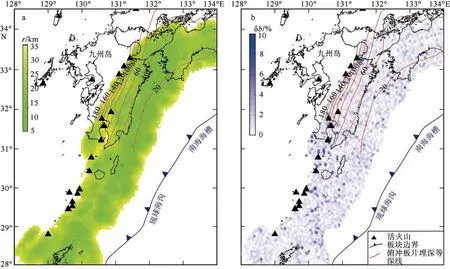
图4 b 值成像的扫描半径r(a)和b 值的标准误差δb(b)分布特征 俯冲的菲律宾海板块上边界埋深等深线用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004) Fig.5 (a) Distribution of sampling radius for mapping b-value. (b) Distribution of standard errors of b-value. Depth contours of the upper boundary of the subducting Philippine Sea slab are shown in red with an interval of 20 km (Wang et al, 2004)
第二组用于计算九州-帕劳海脊区垂直于海沟的剖面上的b 值: 在剖面上创建一个以2km 为间距的均匀正方形网格, 以网格节点为圆心, 在以最小半径为1km、最大半径为10km 的圆形范围内从小到大依次对地震进行筛选和统计, 获得地震事件集N2; 根据地震事件集N2计算相应的MC, 滑动步长为1km; 要求每个节点圆内震级M≥MC的地震数不少于30 个, 且以网格节点为圆心, 以10km 为半径的范围内至少有1 个地震事件。此组参数计算得到的结果与第一组参数类似, 均能较好地反映该区的地震分布特征, 因此计算结果可靠。
在最近距离-固定事件扫描方法计算的过程中, 各网格点的最小事件数是固定的, 通过变化空间上的扫描半径来完成约束。扫描半径的大小可反映该区地震事件数量的密集程度, 地震数量越多, 满足模型数量要求的空间范围越小, 扫描半径就越小; 反之则越大。计算结果显示, 以九州东部20~40km的等深线范围为中心的扫描半径最小, 扫描半径向东西两侧逐渐变大(图4a); 对应于实际深度即为菲律宾海板块俯冲深度20~80km 之间的区域, 扫描半径大小主要在20km 范围内。而海上区域和俯冲带深部地震事件数变少, 所以越往深处以及远离海岸的区域扫描半径就越大。鉴于同时兼顾计算结果的准确性和覆盖范围, 本文将最大扫描半径定为35km。从b 值的标准误差分布来看, 误差总体上小于2%, 极少部分误差超过3%(图4b), 说明本文的b值计算结果较为可靠。
1.4 余震分析
由于余震的存在会导致所统计的地震活动的时空分布偏离正常状态(陈凌 等, 1998), 继而影响b值的准确度和代表性, 因此在地震活动性分析和b值计算前, 一般需要剔除余震(盛菊琴 等, 2007; 徐伟进 等, 2017)。为此, 本文对筛选的地震事件进行了统计分析(图5), 从地震随时间的累积曲线可以看出, 曲线基本呈线性趋势, 表明台站记录良好, 受强震和余震影响较小。选择研究区中部区域(130°—133°E, 31°30′—32°30′N), 分别使用含余震和无余震(K-K 法)(Keilis-Borok et al, 1980)的数据计算b 值, 结果显示两种数据得到的b 值总体趋势一致(图6), 因此b 值计算前不需要进行余震删除处理。
2 结果
2.1 总体b 值特征
通过线性回归拟合获得研究区域总体b 值为0.604 (图3) (相对误差为±1.16%), 低于全球平均值(约等于 1), 处于全球俯冲带 b 值平均值范围(0.5~0.8)的中间位置(Ghosh et al, 2008)。该线性拟合适用于使用的整个地震目录以及九州-帕劳海脊两侧区域的事件子集。
图5 地震随时间累积曲线图(a)和地震(M≥0)的震级-时间分布图(b) Fig.5 (a) Cumulative curve of earthquakes with time, and (b) distribution of magnitude-time of earthquake(M≥0)
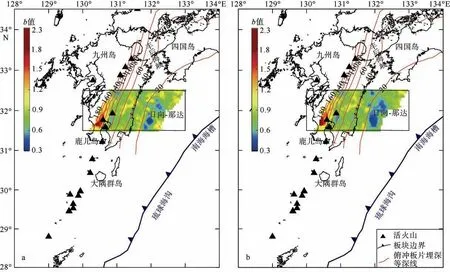
图6 由包含余震的地震数据(a)和删除余震后的地震数据(b)计算得到的b 值分布特征 俯冲的菲律宾海板块上边界埋深等深线用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004) Fig.6 (a) Distribution characteristics of b-value calculated from data that contain aftershocks, and (b) distribution characteristics of b-value calculated from data that contain no aftershocks
根据前文介绍的第一组最优参数计算得到的菲律宾海板块上表面b 值结果如图7 所示。从平面分布来看, 菲律宾海板块俯冲界面的b 值范围介于0.34~2.3, 且具有显著的空间分布差异。以九州-帕劳海脊为界, 东北侧区域的b 值平均值为0.71(相对误差为±1.83%), 西南侧区域的 b 值平均值为0.76(相对误差为±2.5%)。总体上, b 值沿着南海海槽和琉球海沟轴线方向从东北向西南逐渐增大, 这与前人研究的结果基本一致(Nanjo et al, 2018; Chiba, 2019)。
2.2 九州-帕劳海脊两侧的b 值特征
九州-帕劳海脊东北侧区域的b 值介于0.34~0.8之间(图7)。其中, 丰后海峡和四国岛北部的b 值相对较低, 在空间上主要集中在俯冲板片埋深20~60km 之间以及俯冲板片倾角较缓的区域(图7 等深线较稀疏的区域), 这也与前人研究结果较为一致(Nanjo et al, 2018; Chiba, 2019)。在九州-帕劳海脊的西南侧区域, b 值整体较高, 其中九州南部鹿儿岛及其以南区域的b 值最高, 从0.8 到2.3, 相对误差范围为0.01%~10%。值得注意的是, 这一区域的俯冲板片倾角较海脊东北侧略大, 且从80km 深度往下俯冲倾角急剧增大(Nakajima, 2019)。
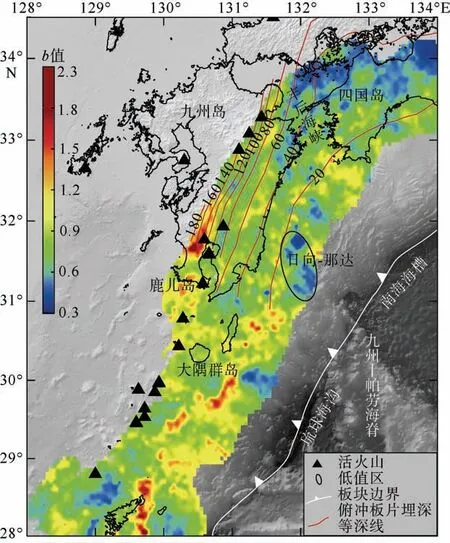
图7 菲律宾海板块上表面b 值分布特征 俯冲的菲律宾海板块上边界埋深等深线用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004) Fig.7 Distributive characteristics of b-value on both sides of Kyushu-Palau Ridge
2.3 九州-帕劳海脊的b 值分布特征
沿着九州-帕劳海脊俯冲的延伸方向, 根据b 值高低可以分为两个区域。其中靠近海沟处, 在九州岛东南侧海域日向-那达下方的俯冲板片上出现了一个范围较小的显著低b 值区(见图7 黑色椭圆区域), b 值为0.34~0.8, 此区域内各个节点b 值的相对误差小于4%。从穿过俯冲海脊的4 个垂直剖面上可以看出, 该低b 值区位于俯冲的菲律宾海板片内部, 深度在20~30km 之间(图8)。
沿俯冲海脊走向往西北方向, 在九州岛中部的下方位置, b 值明显变大, 范围介于0.7~1.1 之间, 相对误差小于5%, 略高于海脊东北侧区域(33°N 以北), 而低于西南侧(31°N 以南)区域, 表现出从东北侧年轻洋壳区向西南侧年老洋壳区过渡的特点。
3 讨论
3.1 b 值反映的汇聚作用特点及其成因
鉴于b 值与差应力呈负相关关系, 从上述的b值分布特征可以看出, 菲律宾海板块俯冲界面的差应力沿南海海槽-琉球海沟走向从东北向西南呈逐渐变小的趋势。其中, 东北部的丰后海峡和四国地区受到的差应力较大, 表明俯冲的四国海盆洋壳与上覆板片之间的耦合程度相对较强。相比之下, 九州-帕劳海脊的西南侧区域, 俯冲的西菲律宾海盆洋壳与上覆板片之间的耦合程度相对偏弱。究其原因, 主要是九州-帕劳海脊两侧截然不同的洋壳属性起了重要作用(表1)。
对于海脊东北侧来说, 由于该区洋壳较年轻(Okino et al, 1994), 俯冲板片具有相对较高的温度(徐纪人 等, 2003)和相对较低的密度, 由此表现出较高的浮力(Nishikawa et al, 2014), 不易于俯冲到大陆板块之下。另一方面, 海底的速度场研究也显示海脊东北侧的年轻板块移动速度比西南侧快(Yokota et al, 2016)。这些因素导致了海脊东北侧的俯冲板片与上覆板片之间的耦合力更强, 俯冲之后的板片倾角也更缓, 从而积累了更大的应力, 表现出低b 值的特点。该区汇聚板片之间较强的耦合作用(Ghosh et al, 2008)也可以从陆域GPS 的观测结果(徐纪人 等, 2003)得到证实。
在海脊西南侧, 较早的形成时代意味着这一区域的洋壳具有较低的温度、较高的密度和较低的浮力, 在俯冲时与上覆板片之间的作用力更弱, 从而更易于俯冲。因此, 较高的b 值反映了汇聚板片之间的耦合程度相对较弱。
3.2 九州-帕劳海脊的俯冲及其对地震活动性的影响
海脊(海山)俯冲一直是俯冲带研究的一个热点问题(李付成 等, 2016)。九州-帕劳海脊地壳厚度约为15km, 平均宽度约为90km, 如此规模的海脊俯冲, 其研究更是广受瞩目(Nishizawa et al, 2009; Park et al, 2009; Yamamoto et al, 2013)。
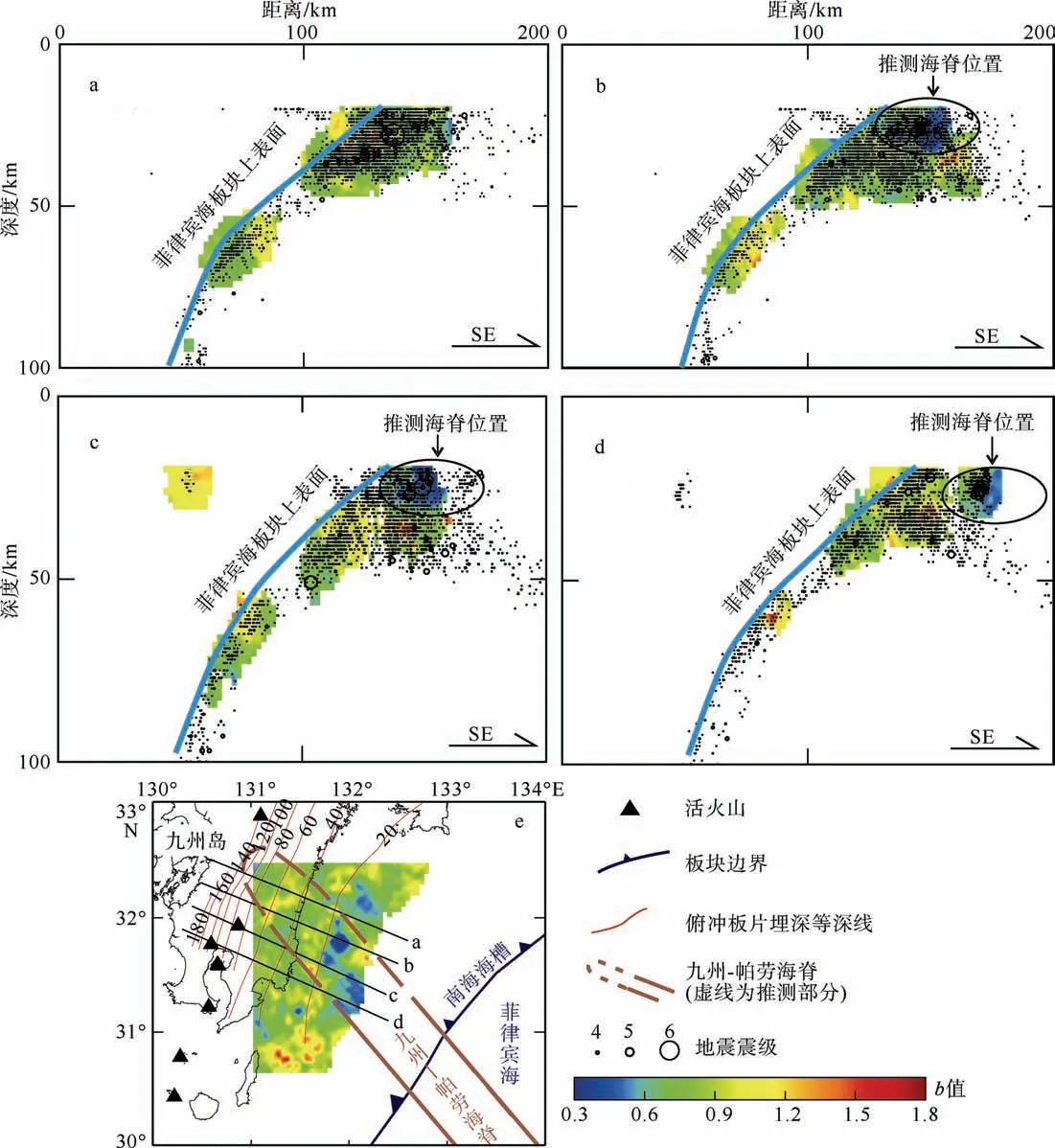
图8 垂直于海沟的剖面b 值分布特征(a—d)及剖面位置示意图(e) 图a—d 中的地震大小均以震级乘以同个系数成图, 图例中只列出4 级、5 级和6 级作为地震大小参考; 图e 中俯冲的菲律宾海板块上边界埋深等深线用间隔为20km 的红色曲线表示, 数据来源于Wang 等(2004) Fig.8 Distribution of b-value along the cross-sections of a, b, c, and d of the Kyushu-Palau Ridge profile
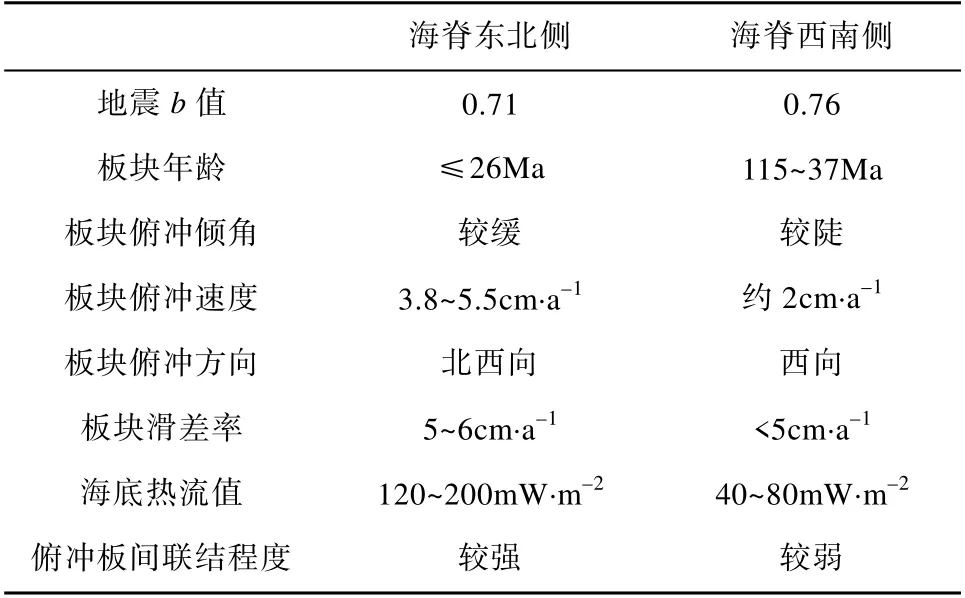
表1 九州-帕劳海脊两侧的洋壳特征 Tab. 1 Regional characteristics of the north and south sides of the Kyushu subduction zone
从九州-帕劳海脊的b 值特征来看, 俯冲带浅部为低b 值区, 表明该区累积了较大的应力, 这可能是隆起的海脊进入俯冲带后与上覆板片发生了强烈的剪切-挤压所致。Chiba(2019)通过研究该区的长期慢滑移事件和低频地震事件, 也证实该低b 值区可能积累了巨大的剪切应力。随着深度的增加, 沿俯冲方向海脊区的b 值逐渐增高, 表明俯冲的海脊与上覆板片之间的耦合作用大幅减弱。考虑到九州-帕劳海脊的地壳厚度接近于典型洋壳厚度的2 倍(Nishizawa et al, 2009), 加之该处的俯冲深度、相对较高的汇聚速率和逐渐变陡的板片倾角, 这一现象是不正常的。因此, 俯冲的九州-帕劳海脊极有可能如地震层析成像结果显示的那样, 沿着海脊走向发生板片撕裂(Cao et al, 2014)。从本文的结果推测, 板片撕裂范围可能要比地震层析成像显示的深度更浅。在板片撕裂之后, 东北、西南两侧不同时代的洋壳板片由此断开, 从而降低了与上覆板片的耦合程度。相对于俯冲带浅部尚未撕裂的海脊, 撕裂区域附近的b 值也就大幅度地升高了。实际上, 板片俯冲后沿海脊(海山链)走向发生板片撕裂的现象并不鲜见(Bautista et al, 2001; 刘再峰 等, 2007), 只不过九州-帕劳海脊的撕裂除了受自身先存的薄弱带和隆起的板片影响之外, 两侧不同时代的洋壳也起了重要作用(表1)。
海脊俯冲往往会增强对应区域的地震活动, 如智利中部的胡安-费尔南德斯海脊(Anderson et al, 2007)和瓦努阿图俯冲带的 D'Entrecasteaux 海脊(Baillard et al, 2018)。对本文研究区来说, 位于日向-那达下方的低b 值区可能是一个潜在的强震震源区。
4 结论
以九州俯冲带的b 值计算结果为依据, 对该区的空间应力分布特征和板块汇聚作用进行了分析与讨论。b 值计算结果显示, 菲律宾海板块俯冲界面上的b 值存在显著的空间差异, 整体上从东北向西南方向逐渐变大, 表明俯冲板块界面的差应力沿南海海槽-琉球海沟走向从东北向西南逐渐变小。这一特征主要是由于九州-帕劳海脊两侧截然不同的洋壳属性所致, 两侧洋壳在形成时代和汇聚速率上的差异导致两者与上覆板片的作用力明显不同, 造成东北侧俯冲板片具有较强的耦合力, 而西南侧耦合程度相对较弱。此外, 沿九州-帕劳海脊的俯冲方向, 日向-那达下方的低b 值区可能是由进入俯冲带的海脊与上覆板片发生强烈剪切-挤压所致; 随着俯冲深度的增加, b 值显著升高, 这与俯冲至九州岛下方的板片沿海脊发生撕裂有关。
