基于行业视角的我国养老金股票市场资产配置研究

周 延，潘荣旭

（华东师范大学 经济与管理学部，上海200062）

一、引言

基本养老保险在我国养老保险体系中的资金占比一直维持在50% 以上，2017年占比达到59%①，其对于国家的经济发展、社会的和谐稳定及人民的生活保障所起的作用毋庸置疑。但是，伴随着老龄化的快速推进，近年来关于养老金捉襟见肘的探讨频频见诸报端。根据中国社科院世界社保研究中心最新发布的《中国养老金精算报告2019-2050》预测，未来30年我国养老金的制度赡养率将翻倍，当期结余将于2028年出现赤字并不断扩大，养老金累计结余将在2035年耗尽，社会养老压力不断增大。

事实上，从2013年开始，全国基本养老保险基金收入持续低于同期支出，养老金缺口逐年扩大，养老金的可持续性问题亟待探讨。鉴于养老金支付体系存在的问题，国务院早在2015年8月就印发了《基本养老保险基金投资管理办法》（以下简称《管理办法》），允许养老金投资股票、债券等资产，试图通过扩大养老保险基金的投资范围，提高养老金的收益来改变这一现状，但实际收益情况却不尽如人意。

另一方面，全国社会保障基金（简称“社保基金”，不同于养老金所属的社会保险基金）作为养老保险等社会保障支出的补充和国家战略性储备基金，自成立以来的年均投资收益率达到7.82%，累计投资收益额为9552.16亿元②，远高于养老金的投资收益，值得养老金投资学习借鉴。社保基金重仓流通股的行业配置整体偏好于“净利润增速较高、净资产收益率较高”的行业，配置比例较高的行业有医药、电子、房地产、计算机、食品饮料等。

自改革开放以来，我国资本市场取得长足发展，为养老保险基金创造了合适的投资环境。中外学者对于养老金的投资问题也提出了诸多不同的观点。20世纪50年代由马科维茨创立，威廉夏普与斯蒂芬罗斯发展推广的现代资产管理理论为养老金组合投资提供了理论依据。以此为基础，西方学者利用数量分析的方法不断完善投资管理办法。Boldrind（1999）研究发现，分散投资能够化解养老金投资的非系统性风险[1]。Booth 和Yakoubov（2000）分析英国保险数据发现，养老金投资中股票投资比例的提升能够有效对冲通货膨胀风险[2]。此外，一些学者也通过计量方法的创新来进行养老金投资研究，例如Choueifaty 和Coignard（2008）首次采用分散化组合法来估计养老金的方差[3]，Maillard（2010）等运用最小方差组合构造在限制卖空条件下的风险配置策略[4]。

我国国内学者也对养老金的投资可行性和投资方法进行了深入研究，并提出许多新观点。安实等（2003）在人寿保险公司最优投资组合决策中嵌入拉格朗日法[5]；安起光和王厚杰（2006）建立了均值-VaR投资组合模型[6]；田玲（2011）等结合经济资本优化配置模型，显著提高了保险公司投资绩效[7]；孟勇（2012）使用贝叶斯移动平均法预测投资者主观收益[8]；考虑到通货膨胀因素，也有学者用均值-方差模型研究连续时间投资组合选择问题（姚海祥，姜灵敏，2013）[9]；徐漫（2016）等则设立相对确信度变量，使投资者能通过更新信息来调整养老金投资组合[10]。在对我国保险资产的投资进行分析时，有学者发现我国保险资金运用存在资产负债理念和技术落后、金融市场产品种类少与期限结构不合理等问题（郭金龙，胡宏兵，2009）[11]，还发现保险资产配置是一个动态优化进程，其配置应从比例配置向模式配置转变（王颢，潘文捷，2016）[12]。

就目前对于养老金资产配置的研究来看，大部分学者倾向于使用马科维茨模型，也就是均值方差模型，但它也有明显的缺点，比如“投资者仅仅是依据证券的风险和收益进行投资”等前期设定过于严格，很难在现实生活中应用。而且模型对于输入数据敏感度很高，即使很小的误差也会导致结果与真实值相去甚远。此外马科维茨模型没有引入行为金融学的理论，即投资者的非理性人假设。投资者会在资产配置时受到自己主观感受的影响，其投资结果并不是绝对理性的。针对于此，本文决定采用Fisher Black和Robert Litterman于1992年提出的Black-Litterman模型（以下简称BL模型），研究其在养老金资产投资优化方案中的可行性。同时参考社保基金的投资方式，创新性地计算养老金在股票市场各主要行业的投资比例，以期提高养老金的投资收益，为养老金拓展和完善新的投资领域及投资方式。

二、我国养老保险基金投资收益现状分析

我国从上世纪末开始探索并建立了“社会统筹与个人账户相结合”的社会养老保险制度。但是由于在此之前的退休职工并没有交过养老金，所以较年轻的在职职工所缴纳的养老保险金并没有直接进入自己的个人账户，而是“统筹”给了老一代的退休职工。长此以往，伴随着人口老龄化问题的日益凸显，就会导致巨额的养老金空账。此外，我国在养老保险基金投资运营初期，为防范风险、维护资金安全等目的，只允许将基金投资于国债和存款，导致收益率很低，并不能满足养老保险基金收益需要。

图1显示了近10年来我国养老金投资收益率的具体变动情况。2009年至2014年我国养老金的实际收益率均低于当期CPI增长率，这就导致养老保险基金不仅无法实现保值增值，甚至有贬值风险，使得基金的收支压力越来越大。近年来股市相对低迷，2015年投资收益率为3.1%，而2016年实际投资收益率仅有1.7%。2017年末，基本养老保险基金已实现收益率4.55%，较2016年有了显著增长，说明养老金入市投资之后对于提高其收益率是有一定帮助的。但2018年由于中美贸易战的影响，我国股市较为低迷，养老金投资收益率仅为2.56%③。

图1 养老金投资收益率变化图

相比于社保基金自成立以来年均7.82%的投资收益率④，养老金的收益率还处在一个较低水平。这一方面是由于之前国家对养老金投资范围进行限制，另一方面也说明养老金的投资水平有待提升。因此，本文参照社保基金投资于股市的方式和行业范围，运用BL模型对养老金在股票市场中的行业配置进行研究。

三、基于BL模型的养老金在股票市场中的行业配置

（一）模型介绍

传统资产配置模型有马科维茨的均值方差模型和威廉夏普的资本资产定价模型，两者共同开创了定量研究资产配置的先河。但是均值方差模型和资本资产定价模型都有着难以避免的不足，它们都未考虑投资者预期对资产配置的影响，实际上不同水平投资者由于获得信息能力以及风险偏好的差异，会导致最终资产配置比例不尽相同。

鉴于此，1992年Fisher Black 和Robert Litterman 提出BL模型。该模型结合均值方差模型和资本资产定价理论，在市场均衡收益分布中加入投资者主观观点来进行资产配置。它弥补了均值方差模型的估计误差缺陷，通过投资者观点的设定，不仅可以验证历史数据，还能够反映后验收益效果。目前BL模型已经成为现代资产配置领域的重要模型。BL模型的框架主要有以下几个部分：

（1）逆优化求解先验收益。在有效市场假说成立也即市场均衡的假设下，通过目前资产的市值权重wmkt、各资产之间超额收益的协方差矩阵∑、风险厌恶系数λ，逆优化求解出市场隐含均衡收益率∏。用公式表示为：

（2）设置投资者观点。对于投资者观点的计算主要涉及参数有观点矩阵向量P（k×n），观点收益向量Q（k×1），观点误差矩阵Ω（k×k）。

（3）在市场均衡收益分布中加入投资者观点，形成后验收益。其中，后验收益E（R）的计算公式为：

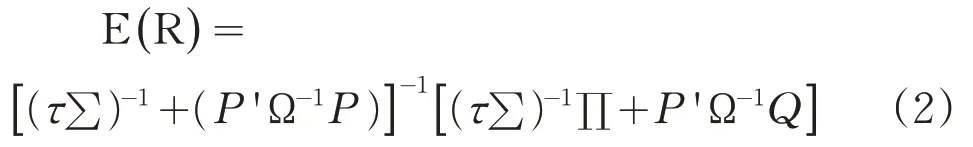
公式（2）中，τ表示调整系数；P代表投资者观点矩阵；Q代表观点收益向量；Ω代表观点误差矩阵。

（4）基于马科维茨模型，将后验收益带入效用最大化约束模型，得出资产配置比例：

根据公式（3）可以求得各资产最优权重为：

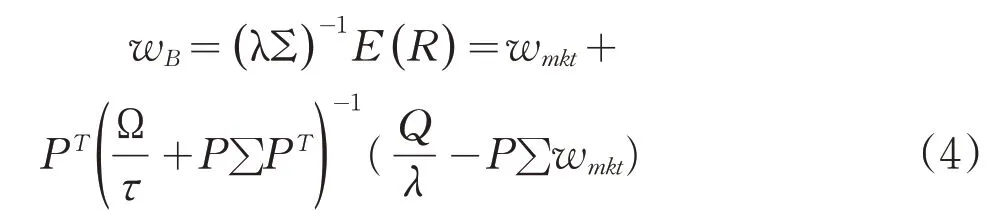
（二）运用GARCH模型预测各行业未来收益率

1.标的行业选取

养老金的配置风格类似社保基金，但风险容忍度更低、流动性需求更高。社保基金对A股的配置风格以价值板块为主、新兴成长为辅，从2012年以来社保基金各行业配置比重看，偏好行业包括医药、传媒、化工、电子、房地产、计算机、食品饮料、建筑、汽车等。因此，本文采用申银万国的行业指数分类，选取电子、食品饮料、医药生物、房地产、计算机、汽车、传媒、化工8个标的行业，并以其从2010年1月4日开始至2019年2月23日近10年的指数相对于前一交易日的涨跌幅作为收益率⑤，对养老保险基金进行行业资产比例配置研究。

2.标的行业描述统计

表1是电子、食品饮料、医药生物、房地产、计算机、汽车、传媒、化工8个行业近十年的指数收益率的描述统计情况。从表1中可以看出，电子、食品饮料、计算机等行业的指数收益率平均值较高，其中计算机行业指数的收益率平均值超过了5%，与近十年我国计算机这一行业发展较快的实际吻合。表1中大部分行业的标准差低于2，说明各行业的指数收益率波动性较小，所有行业的偏度均小于0，说明数据在左侧有较多的极端值，分布不对称。

表1 各行业指数收益率的基本统计量

3.ADF检验

在MATLAB 中使用adftest 公式检验各行业指数收益率的平稳性得到表2。从表2中可以看出，8个行业的收益率序列是平稳的，可以进行未来收益率的预测。

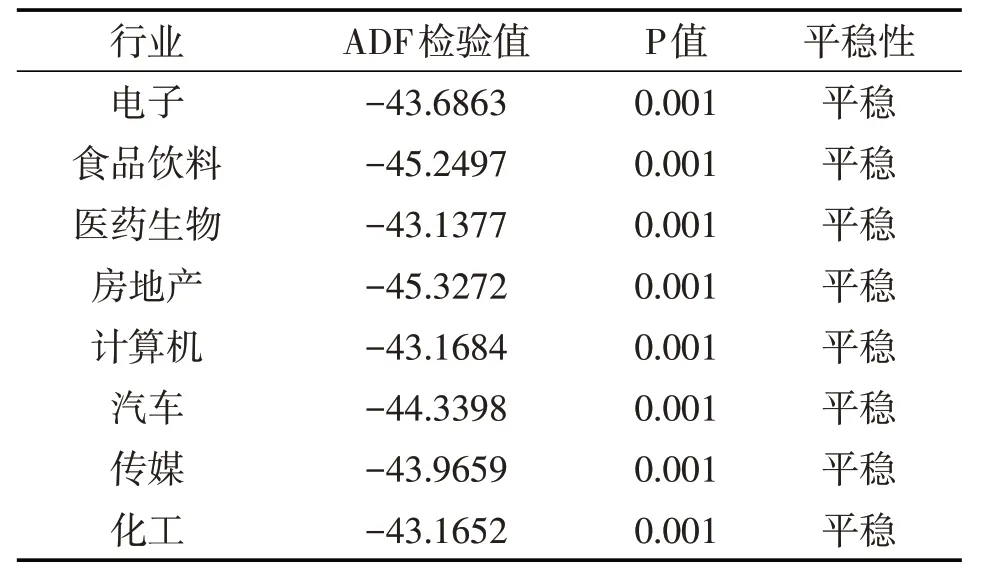
表2 指数收益率的ADF检验结果

4.GARCH模型预测行业指数未来收益率

本文采用广义自回归条件异方差模型（GARCH）预测资产指数未来收益率。用公式表示为：

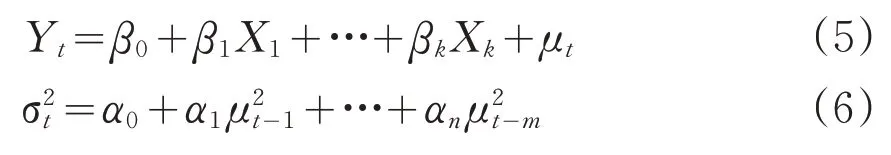
其中，D(μt)=σ2(t=1,2…)称为{μt} 服从m阶的ARCH 过程，即μt～ARCH(m)。从公式（6）可以看出，时刻t的条件方差σ2t依赖于前期残差{μt} 。通俗来说，就是当序列在某一时刻的波动较大时，其后面的波动也会随之增大，这就是ARCH效应。

ARCH模型在提出之后，得到许多学者的应用，也解释了许多资本市场上收益率的波动现象，但是其自身也存在一些缺点。针对于此，1985年Bollerslev提出了GARCH（n，m）模型，该模型认为前期误差项也对当期误差项有影响，用公式表示为：

其中，{Yt}为因变量，在本文中可表示为滞后期指数收益率序列，{Xt}为自变量，本文中可表示为先验行业指数收益率序列，{μt}是无序列相关性的随机扰动项，{σt}为方差序列。本文结合实际情况采用GARCH（1，1）模型。由于计算具有可重复性，这里只对电子行业的收益率过程进行说明，其余行业与之同理。

首先用EXCEL 对电子行业指数的收益率进行普通最小二乘（OLS）估计，得到表3：

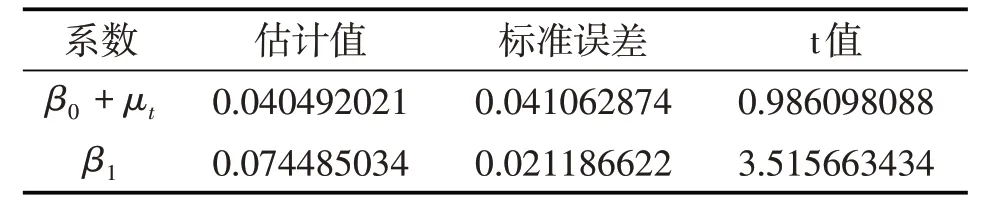
表3 电子行业指数收益率OLS回归结果

对照方程（8）得到电子行业的期望收益估计方程为：

将电子行业的指数收益率导入MATLAB中，运用金融计量工具盒中的GARCH模型，计算得到表4：

表4 电子行业GARCH模型方差方程参数估计

由表4可以看出三个变量的p值均趋近于0，在1%的置信度水平下都是统计显著的，可以得到方差方程为：

重复上述步骤，可以得到其它行业指数收益率和方差的预测值，求出结果得到表5：

表5 8个行业的GARCH模型估计结果

计算机汽车传媒化工0.054867173 0.011655373 0.022757374 0.002328631 28.67966647 1.429257043 5.081080832 0.17964487行业 Ŷt σ̂t 2

（三）BL模型参数设置

1.隐含均衡收益向量

根据公式（1），求解隐含均衡收益，需要计算资产的市值权重wmkt、各资产之间的协方差矩阵∑、风险厌恶系数λ，下面就对这几个变量的求解分别作出说明。

（1）市值权重wmkt。对于各行业指数的市场权重wmkt，本文采用指数所包含的成分股的流通市值来计算，以2019年2月22日收盘时流通市值为准，计算结果如表6所示。由于申万对于行业的分类较为细致，共有28个行业，因此每个行业所占的权重都不会很高，从表6中也可以看到，医药生物行业的流通市值权重最高也仅为6.17%，流通市值最低的行业为传媒行业，权重为2.52%。

表6 各行业指数市场权重

（2）各资产之间超额收益率的协方差矩阵∑。协方差矩阵主要用来衡量行业之间的相关性，其计算结果如表7所示。

表7 各行业指数超额收益率协方差矩阵（%）

传媒化工3.26 2.90 1.90 1.89 2.59 2.35 2.26 2.40 3.55 2.89 2.58 2.59 3.66 2.61 2.61 2.73电子 食品饮料 医药生物 房地产 计算机 汽车 传媒 化工

（3）风险厌恶系数λ。风险厌恶系数又称为风险规避系数，一般用来度量整个市场的风险规避水平，其大小只和市场整体环境相关，而与投资者个人无关，它的计算公式为：

其中表示股票市场的收益率均值，Rf为无风险收益率，本文用银行一年期定期存款利率表示，σ2m表示股票市场收益率的方差。经计算得出风险厌恶系数为1.87。

将市值权重wmkt、各资产之间的协方差矩阵∑、风险厌恶系数λ 代入公式（1），可以得到市场组合的超额隐含均衡收益率向量Π，如表8：

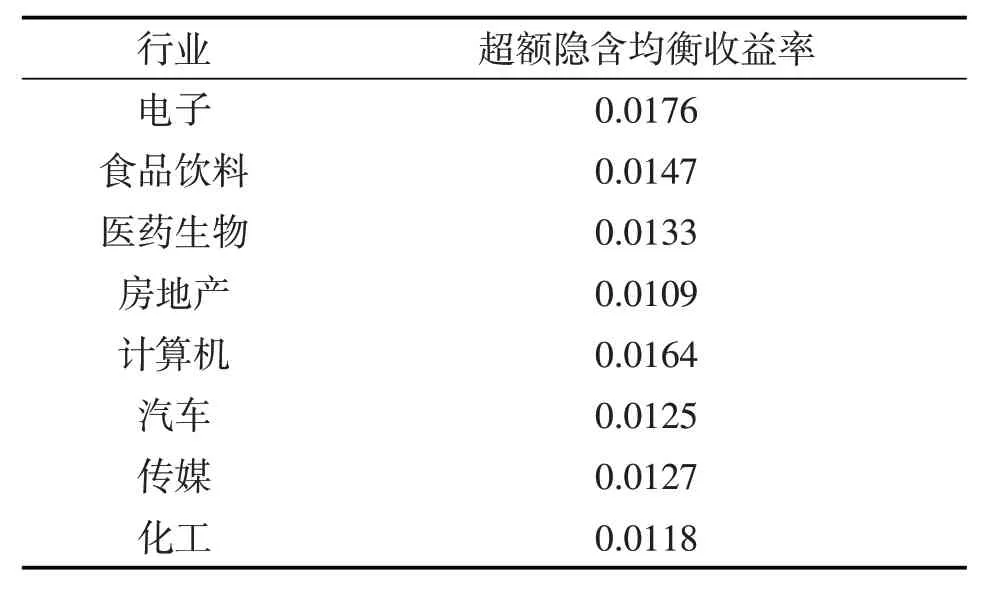
表8 行业超额隐含均衡收益率

2.投资者观点

在BL模型中，如果投资者对于各类资产都有自己的主观预期收益，而且都是绝对观点的话，那么投资者观点矩阵向量P就是n阶单位矩阵，因此本文的投资者观点矩阵就是8×8阶单位矩阵。本文把由GARCH模型预测出来的收益率作为BL模型的观点收益向量Q，即表5第二列所示。观点误差矩阵采用由GARCH模型预测出来的残差开方得到。

3.后验收益

在后验收益的计算公式中，还需要对调整系数τ的具体数值进行计算。调整系数τ表示超额隐含均衡收益和投资者观点收益占后验收益的比值。对于τ值的确定，不同学者有着不同看法，但是大部分学者对于τ值的设立都在0 到1 之间，本文假设投资者主观信心是中性的，即设定τ值为0.5。

到这里，计算后验收益E（R）的公式（2）中的各个变量的数值已经设定完成，参考公式（2），将其带入MATLAB中，进行矩阵运算可以得到后验收益结果，如表9所示：

表9 BL模型后验超额收益

将计算结果与市场实际超额收益率进行对比得到表10：

表10 8个行业实际超额收益率与改进超额收益率对比（%）

从中可以看到，经过BL模型的计算改进，8个行业的超额收益率较实际市场的超额收益率都有超过1%的增加，说明了BL模型对于提高养老金的投资收益是有作用的，接下来就是确定对各行业的投资比例。

（四）BL模型最优权重确定

将隐含均衡收益向量、投资者观点、后验收益计算结果带入公式（4）并输入MATLAB进行矩阵运算，得到表11：

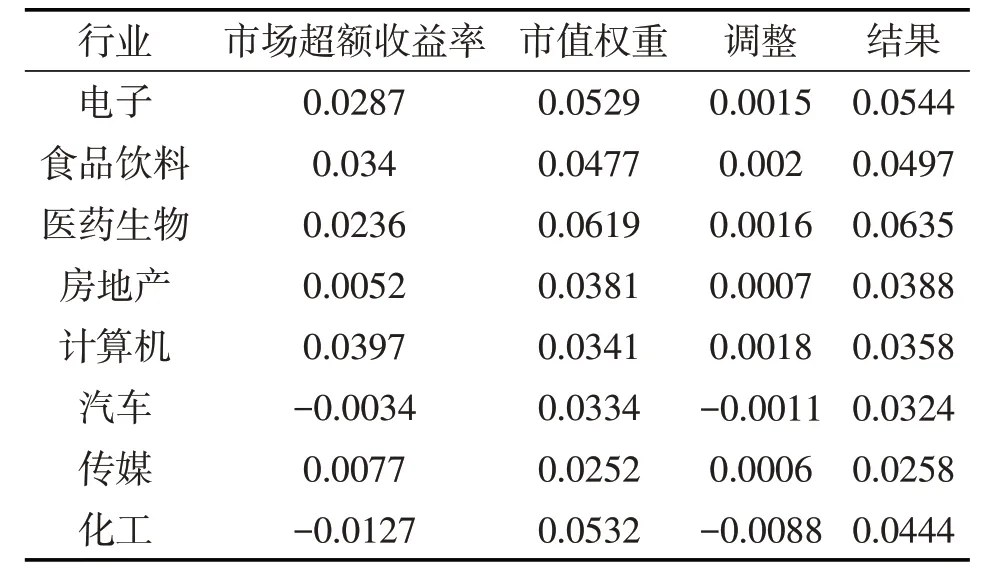
表11 8个行业最优投资权重

（五）BL模型计算结果分析

从表11 中可以看出，当汽车和化工行业的市场超额收益率小于0时，BL模型计算得到的最优投资方式是减少对它们的投资比例，这与我们的实际经验是吻合的。但是对于收益率较高的行业，比如计算机行业，BL模型并没有一味增加对它的投资比例，因为还要考虑到收益率的稳定性，相对于其它行业，计算机行业的收益率预计方差高于其它行业，波动性较大，不能契合养老保险基金的稳健投资要求。

目前主流的行业资产配置方式主要考虑的是各行业的盈利周期和未来发展前景。这种配置方法基本参考了个股的研究范式，区别仅仅在于研究标的有所扩大。许多学者都认为未来并不是对历史的简单重复，而且由于各行业受国家政策的影响巨大，因此对于行业的技术性分析框架研究较少。而本文基于BL模型的养老金行业资产配置研究，发现基于基本面的量化模型在一定程度上能够提高市场超额收益，利用市场的历史信息可以获得一定的套利空间。因此，未来机构投资者以及养老保险投资基金投资人在进行资产配置时，要充分重视量化的行业配置方法，同时也需要开发一些适合中国市场的量化行业资产配置模型。

四、结论与建议

（一）结论

在目前我国养老金入市投资方兴未艾，以及养老金支付体系出现各种问题的背景下，本文首次提出采用BL模型来研究养老保险基金在股票市场中各行业的配置比例问题。BL模型弥补了传统均值方差模型的不足，而且，结合投资者观点增加了资产配置的可信度。在运用BL模型时，本文同时还采用GARCH模型来预测养老保险基金重点关注的8个行业未来收益率，最终计算得出养老保险基金投资重点、投资行业的预期收益率和投资权重。具体来说，本文的研究结论主要有以下两点：

（1）行业指数的收益率和其波动率变化较为复杂，但是考虑到行业收益率具有长记忆性和时变波动，并进一步通过ADF检验得到验证，本文提出采用GARCH模型来预测养老保险基金重点关注的8个行业未来收益率，预测结果显示其可以刻画行业收益率序列的一些分布特征，模拟效果较好。

（2）本文利用GARCH模型拟合收益率，并在BL模型框架下进行养老金的股票市场行业资产配置，得到了较为客观的超额收益。该超额收益相较于市场水平，在风险没有提升的情况下，收益有所提升，不仅为我国养老金的投资创造新的可能，也为机构投资者以及养老保险投资基金投资人提供借鉴和参考。

（二）建议

1.借鉴国外养老金投资经验和先进管理方式

我国养老金投资起步较晚，而国外发达国家经过长时间的发展，已经积累了很多先进的养老金投资经验，因此，我们可以通过研究国外养老金成功投资的案例，再结合我国实际情况，引入前沿养老金管理方式，例如利用本文所述的BL模型来优化我国养老金的资产配置。

2.建立养老金管理人考核制度

由于BL模型中加入了投资者主观观点，其投资应用效果很大程度上取决于资产管理人的管理水平，所以养老金运用需要建立动态的管理人考核制度，设立市场化的筛选机制，选择符合条件的资产管理人，之后设置合理考评机制，根据管理人的投资绩效，对其管理水平进行评价。对投资收益较好的管理人进行相应激励，对投资收益不达标的管理人进行更换，保证BL模型的主观观点设定准确，实际效果不受较大影响。

3.稳步投入市场并合理管控投资风险

股票市场不同于货币市场和债券市场，其风险更高，波动更剧烈。而且养老金的体量较大，如果短时间内将养老金全部投放到市场中的话，会造成市场的剧烈波动，影响投资的实际效果。因此，应当根据实际情况分时段、分批、分行业稳妥投放股市，例如先投放于电子、食品饮料、计算机等高收益的行业。同时在引入新的资产管理方法时，还需要注意应当在局部地区先试点，等投资效果显现之后再推广至全国。

4.健全养老金运用监管体制

银监会和保监会的合并，意味着我国金融行业混业监管的大幕已经拉开。在此背景下，我国应当加快养老金入市相关法律法规建设。由于养老金运用具有投资类型广、风险水平不一的特点，对监管要求较高，因此，还应当建立适当的风险预警机制，对于资金运用过程中可能出现的问题做到防患于未然。此外，监管人员的定期培训也不可或缺，只有吸纳投资监管专业人才，定期对监管人员进行培训，强化监管队伍人才建设，才能实现对保险资金运用的有效监管。

[注 释]

①数据来源于人社部、全国社会保障基金理事会。

②资料来源于全国社会保障基金理事会社保基金年度报告（2018年度）。

③数据来源于全国社会保障基金理事会基本养老保险基金受托运营年度报告（2018年度）。

④资料来源于全国社会保障基金理事会社保基金年度报告（2018年度）。

⑤选取这一时间段的原因在于其长度足够熨平股票市场的波动对于指数收益率的影响，并且对于接下来的计算分析有一定的参考价值。