基于扩散方法的分布式随机变分推断算法
2021-03-04付维明秦家虎朱英达
付维明 秦家虎 朱英达
在大数据时代,数据通常会被分布式地存储在多个节点上,例如传感器网络[1−3]和分布式数据库[4]中等,其中每个节点只拥有部分数据.考虑到单个节点的存储容量有限以及保护数据隐私或安全的需求[5−6],通常无法将所有数据都发送给一个中心节点,然后利用集中式的方法处理这些数据,因此开发高效的算法对分布式存储的数据进行挖掘已成为当前一个重要的研究方向[7−12].
变分贝叶斯(Variational Bayesian,VB)推断[13]是一种功能强大的数据挖掘技术,被广泛用于解决实际问题,如识别文档主题[14−15],对数据进行聚类和密度估计[16]以及预测未知数据[17]等.近年来,研究者们已提出很多分布式的VB 算法[3,18−20],然而在大多数这些算法的每步迭代中,都需要基于整个数据集更新全局参数,这不仅会导致算法计算代价大、效率低,还会导致算法可扩展性差,难以扩展到在线学习或者流数据处理的情况.
随机变分推断(Stochastic variational inference,SVI)[15]的提出使得贝叶斯推断方法在处理海量数据时具有更高的效率和可扩展性.它借用了随机优化的方法,根据基于子样本的噪声自然梯度来优化目标函数,大大减小了每步迭代时所需的存储量和计算量.目前已有一些研究者将其扩展为分布式版本,以提高分布式数据的处理效率以及将其应用于分布式数据流的处理[21].具体地,文献[22]提出了一种有中心的异步分布式SVI 算法,该算法中的中心节点负责收发全局参数,其余节点并行地更新全局参数.值得一提的是,这类有中心的算法往往会存在鲁棒性差,链路负载不平衡,数据安全性差等缺点.在文献[11]中,交替方向乘子方法(Alternating direction method of multipliers,ADMM)[23]被用来构造两种无中心的分布式SVI 算法,克服了有中心的算法的缺点,但它们存在每步迭代中全局参数本地更新所需的计算代价大以及不适用于异步网络的缺点.
本文以SVI 为核心,借用多智能体一致优化问题中的扩散方法[24],发展了一种新的无中心的分布式SVI 算法,并针对异步网络提出了一种适应机制.在所提出的算法中,我们利用自然梯度法进行全局参数的本地更新,并选择对称双随机矩阵作为节点间参数融合的系数矩阵,减小了本地更新的计算代价.最后,我们在伯努利混合模型(Bernoulli mixture model,BMM)和隐含狄利克雷分布(Latent Dirichlet allocation,LDA)上验证了所提出的算法的可行性,实验结果显示所提出的算法在发现聚类模式,对初始参数依耐性以及跳出局部最优等方面甚至优于集中式SVI 算法,这是以往分布式VB 算法所没有表现出来的.
本文其余部分安排如下:第1 节介绍集中式SVI 算法;第2 节介绍本文所提出的分布式SVI算法并给出了一种针对异步网络的适应机制;第3 节展示在BMM 和LDA 模型上的实验结果;第4 节对本文工作进行总结.
1 随机变分推断
1.1 模型介绍
SVI 基本模型包含以下这些量:数据集x={x1,···,xN},局部隐藏变量y={y1,···,yN},全局隐藏变量β以及模型参数α.模型的概率图如图1所示,其中黑色圆圈代表固定参数,灰色圆圈代表数据集,白色圆圈代表隐藏变量,箭头描述了它们之间的依赖关系.具体地,α直接影响β,β直接影响局部变量对 (xn,yn).我们假设全局隐藏变量β的先验分布属于指数族分布且具有如下形式:
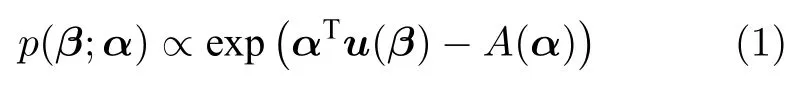
其中,u(β) 表示自然参数,A(α) 表示归一化函数;不同局部变量对 (xn,yn) 之间相互独立且其分布也属于指数族分布,具体形式如下:
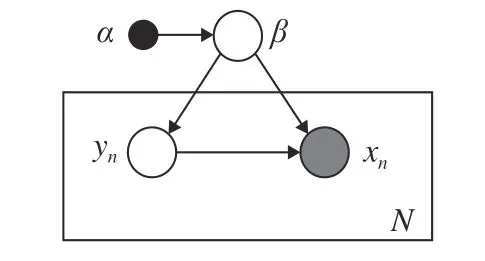
图1 本文考虑的模型的概率图表示Fig.1 The graphic model considered in this paper

其中f(xn,yn) 表示自然充分统计量;此外,还假设上述两个指数族分布满足共轭条件关系[25],以使后验分布与先验分布的形式相同.我们的目标是根据观测到的数据集来估计局部隐藏变量的分布,即其后验分布p(y,β|x).
1.2 平均场变分推断
平均场变分推断是一种用一个可以因式分解的变分分布去近似后验分布的方法.在上一节介绍的模型基础上,我们可以用变分分布q(y,β) 来近似p(y,β|x),并假设该变分分布满足以下条件:
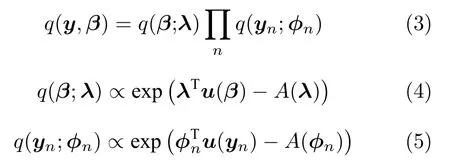
其中,λ和φ={φ1,φ2,···,φN} 是变分参数.此时需要最小化q(y,β)和p(y,β|x) 之间的Kullback-Leibler (KL)散度来让q(y,β) 逼近p(y,β|x),这等价于最大化
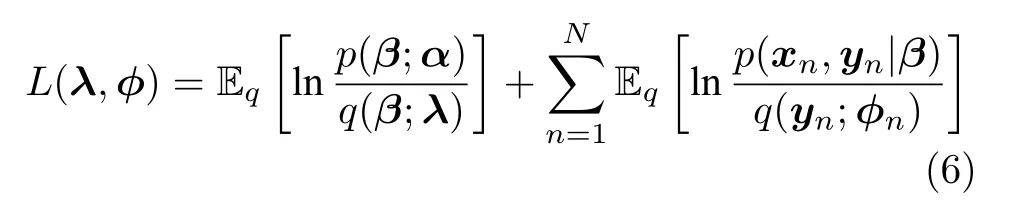
其中,Eq[·]表示在分布q(y,β) 下的期望函数,L(λ,φ)是对数证据 lnp(x) 的一个下界,被称为Evidence lower bound (ELBO)[15].基于q(y,β)) 可分解的假设,最大化L(λ,φ) 可以利用坐标上升法[26]通过交替更新λ和φ来实现.下文讨论的SVI 以上述平均场变分推断方法为基础.
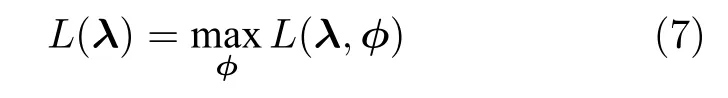
如果我们固定φ,则可以把L(λ,φ) 看成是λ的函数,此时需要求解常用的方法是对其求(欧氏)梯度,但是用欧氏距离表征不同λ之间的远近关系是不合理的,这是因为λ为变分参数,我们所关心的是不同的λ所刻画的分布q(y,β) 之间的差异,此时可以引入自然梯度[15],它表示的是函数在黎曼空间上的梯度.通过对L(λ,φ)关于φ求自然梯度,可以将平均场变分推断推广到随机优化的版本,即随机变分推断.具体地,我们定义如下的随机函数
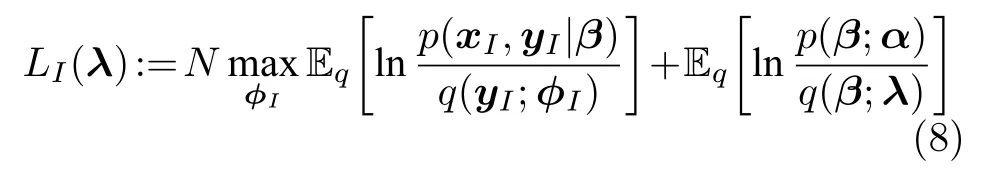
其中,I是均匀取值于{1,···,N}的随机变量.易知LI(λ)的期望等于L(λ),因此每次均匀地选取一个数据点n时,Ln(λ) 给出了L(λ) 的一个无偏估计.根据随机优化理论,集中式SVI 的过程由下面两步构成:
1) 均匀地随机选取一个数据点n,并计算当前最优的局部变分参数
2) 通过
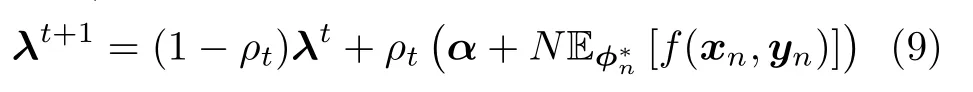
更新全局变分参数λ.
上述SVI 算法一次迭代只采样一个数据点,其也可以被直接扩展成一次采样一个数据批量(Batch)的版本,详见文献[15].
2 基于扩散方法的分布式SVI 算法
2.1 问题描述
我们考虑一个由J个节点组成的分布式网络,其中每个节点i存储包含Ni个数据项的数据集xi={xi1,···,xiNi},于是整个网络上存储的完整数据集为x={x1,···,xJ},总数据项数为假设网络的通讯拓扑是一个无向图G=(V,E),其中V={1,···,J}是节点集合,E ⊆V ×V是边集合,(i,j)∈E表明信息可以在节点i和节点j之间直接传输,记节点i的邻居集合为Bi={j ∈V:(j,i)∈E}.此外,我们还假设G是连通的,即对存在至少一条路径连接节点i和节点j.
如果记节点i的局部隐藏变量为yi={yi1,···,yiNi},记对应的局部变分参数为φi={φi1,···,φiNi},则ELBO 可以写为
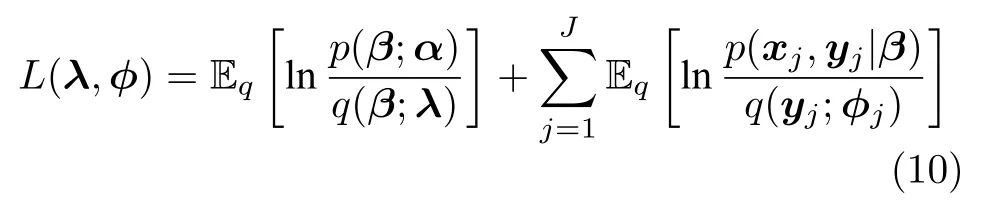
2.2 算法设计
我们借用多智能体一致优化问题中的扩散方法来发展分布式SVI 算法.扩散方法的基本思想是交替执行本地更新和节点间参数融合两个步骤,从而使所有节点的参数收敛到所希望的全局最优值或者局部最优值.
对于节点i,如果定义其局部ELBO 为
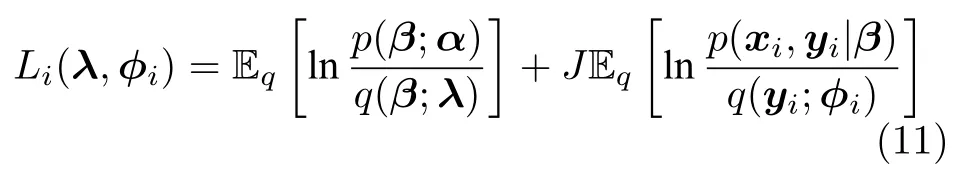
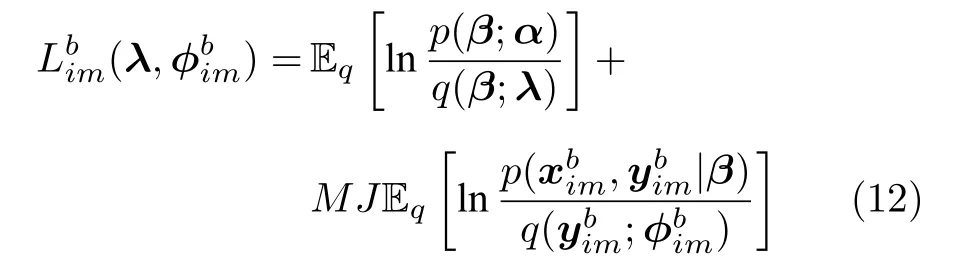

注意本地更新只能使每个节点的全局变分参数独立地收敛到各自的局部ELBO 的局部最优值,我们还要保证每个节点学得的全局变分参数收敛到一致,即||λi-λj||→0,由于我们已经假设拓扑图是连通的,因此只要使||λi-λj||→0,∀(i,j)∈E就可以保证所有节点的全局变分参数都收敛到一致.为此,根据扩散方法,我们在每次本地更新之后,将每个节点的当前全局变分参数发送给其邻居节点,然后将当前的全局变分参数与从邻居节点接受到的全局变分参数进行融合.上述过程可以由下面公式描述:
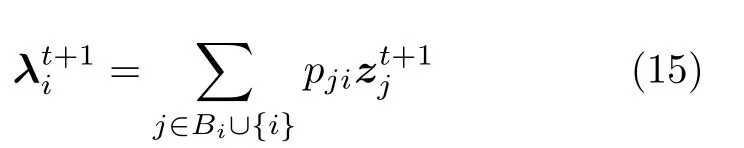
其中,pij是融合系数,我们采用如下的定义
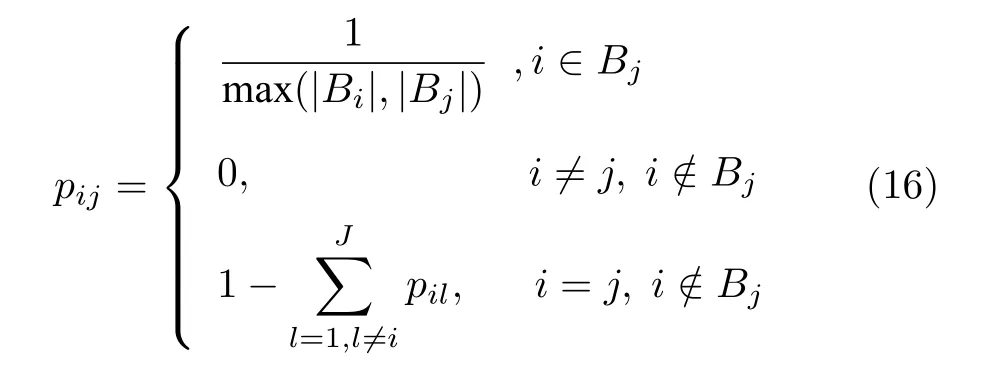
事实上,如上定义的 [pij]是一个对称随机矩阵.当迭代次数很大的时候,ρt变得很小,则有分布式SVI 算法退化成由式(15)描述的平均一致性协同过程,所以将收敛到所有节点初始参数值的平均值.这样使得训练结果不会对任何节点的数据分布有偏向性.
2.3 针对异步网络的适应机制
上节所述的分布式SVI 算法默认是同步执行的,即所有节点在每个迭代步同步地执行本地更新和参数融合两个步骤.但是所有节点同步执行需要使用时间同步协议去估计和补偿时序偏移,这会带来额外的通信负载.此外,执行快的节点需要等待执行慢的节点,这会大大降低算法的执行速度.为此我们设计了一种机制使所提出的分布式SVI算法适应异步通信网络.具体地,每个节点额外开辟一块存储区域将邻居节点发送过来的存储起来.在每个参数融合步中,如果在等待一定的时间后收到了来自邻居节点发送过来的则更新存储区域中的的值,然后,用更新后的进行本地参数更新;否则,直接用存储区域的值进行本地参数更新.这样一来,既可以使所提出的分布式算法以异步方式执行,又尽可能地保证了算法的性能.
3 实验
这一节我们将所提出的分布式SVI 算法(我们称之为异步分布式SVI)应用于BMM 模型和LDA主题模型,并在不同的数据集上测试其性能.并且将其与集中式SVI 算法和dSVB 算法[3]进行对比,其中dSVB 算法被我们以同样的方式扩展成随机的版本以方便比较.
3.1 伯努利混合模型
我们考虑具有K个成分的混合多变量伯努利模型.该模型的全局隐藏变量包括:每个成分k的全局隐藏变量βk,其维度等于数据维度,每个维度的值表示该维度的数据值属于“0”的概率,以及成分的混合概率π={π1,···,πK},其中隐藏变量的先验分布形式如下:
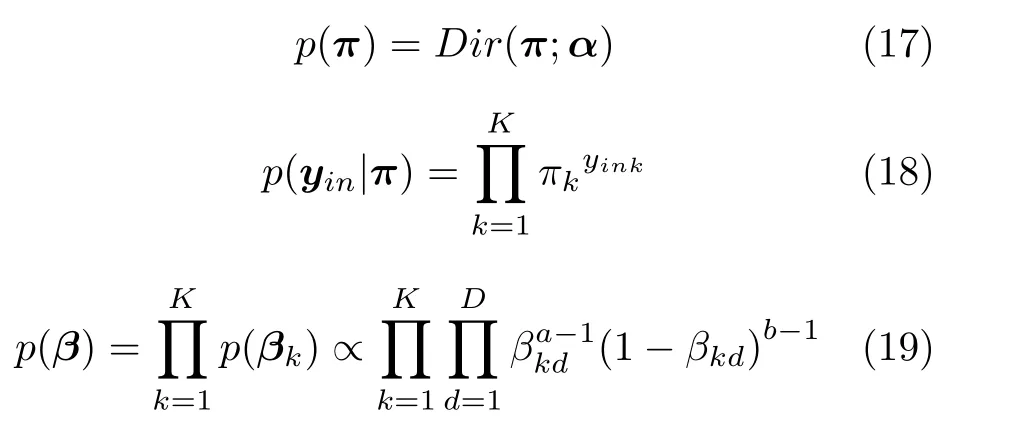
其中,α=[α]K,a和b是固定的超参数,在BMM模型上的实验中,我们均设置α=a=b=1.
我们将混合多变量伯努利模型应用到MNIST 数据集上.在预处理中,每张图的每个像素根据其像素值被设为0 或者1,然后每张图被展开成28 × 28=784 维的向量.我们随机生成包含50 个节点,166 条边的无向连通网络,其拓扑结构如图2所示,并将训练数据平均分给50 个节点,每个节点包含1 200 条数据(整个MNIST 训练集包含60 000条数据).实验中,设置K=40,并设置全局隐藏变量的先验分布为均匀分布.
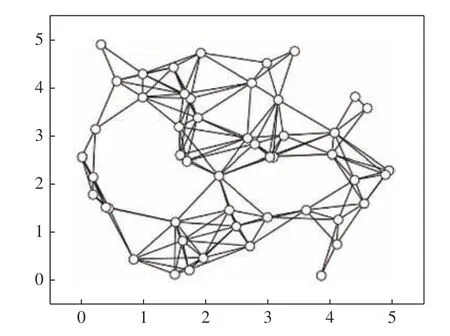
图2 通信网络拓扑图Fig.2 The topology of the communication network
图3 展示了所提出的异步分布式SVI 算法在κ=0.5,τ=10下,每份数据分6 个批次训练200 个epoch 得到的聚类中心 (由每个成分k的全局隐藏变量βk的期望所定义的向量对应的图片) 和相同设置下集中式SVI 算法得到的聚类中心.由图3 可知,异步分布式SVI 算法可以充分找到所有潜在的聚类模式,而集中式SVI 则往往不能充分找出所有的聚类模式.
在相同设置下多次运行三种算法得到的所有节点估计的ELBO 的平均值以及相校平均值的偏差演化曲线如图4 所示,可以看到异步分布式SVI 算法相比集中式SVI 算法能够收敛到更好的值,并且多次运行得到的结果之间的误差更小,表现更加稳定.此外,异步执行的方式破坏了dSVB 算法的收敛性,而异步分布式SVI 算法对异步网络具有良好的适应性.

图3 异步分布式SVI 算法和集中式SVI 算法得到的聚类中心Fig.3 Cluster centers obtained by the asynchronous distributed SVI and the centralized SVI
为了研究超参数κ和τ对所提出的分布式SVI算法表现的影响,我们在(κ=0.5,τ=1),(κ=0.5,τ=10),(κ=0.5,τ=100),(κ=0.75,τ=10),(κ=1,τ=10)几组参数下进行实验,所得到的所有节点ELBO 的平均值的演化曲线见图5,可以看到在不同的 (κ,τ) 设置下所提出的异步分布式SVI 均优于集中式SVI.
3.2 LDA 主题模型
LDA 主题模型是文档集的概率模型,它使用隐藏变量对重复出现的单词使用模式进行编码,由于这些模式在主题上趋于一致,因此被称为“主题模型”.其已经被应用于很多领域,例如构建大型文档库的主题导航或者辅助文档分类.LDA 模型的贝叶斯网络结构如图6 所示,其中变量的说明见表1.
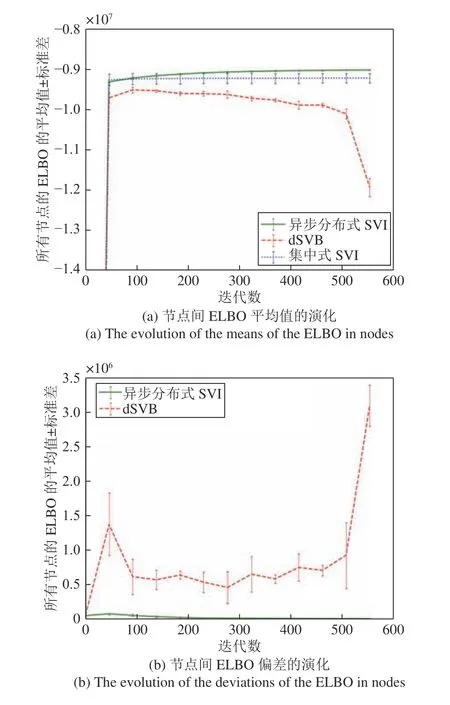
图4 异步分布式SVI 算法、dSVB 算法、集中式SVI 算法的ELBO 的平均值和偏差演化Fig.4 The evolution of the means and deviations of the ELBO for the asynchronous distributed SVI,the dSVB,and the centralized SVI
我们首先在New York Times 和Wikipedia 两个数据集上验证异步分布式算法在LDA 模型上的性能.首先我们生成一个包含5 个节点7 条边的网络,将每个数据集的文档随机分配给各个节点.在实验中我们设置K=5,并以文档集的生成概率的对数作为评价指标.
图7 展示了在α=0.2,η=0.2,κ=0.5,τ=10,训练epoch 取40,分布式算法中每个节点的批大小取10,集中式算法的批大小取50 的设置下,异步分布式SVI,集中式SVI 和dSVB 以异步方式分别在两个数据集上运行多次得到的lnp(w)的演化曲线,可见异步分布式SVI 算法表现优于另外两种算法.不同参数设置下异步分布式SVI 和集中式SVI 在New York Times 数据集上收敛时的lnp(w)见表2,可见不同设置下异步分布式SVI 的表现均优于集中式SVI.
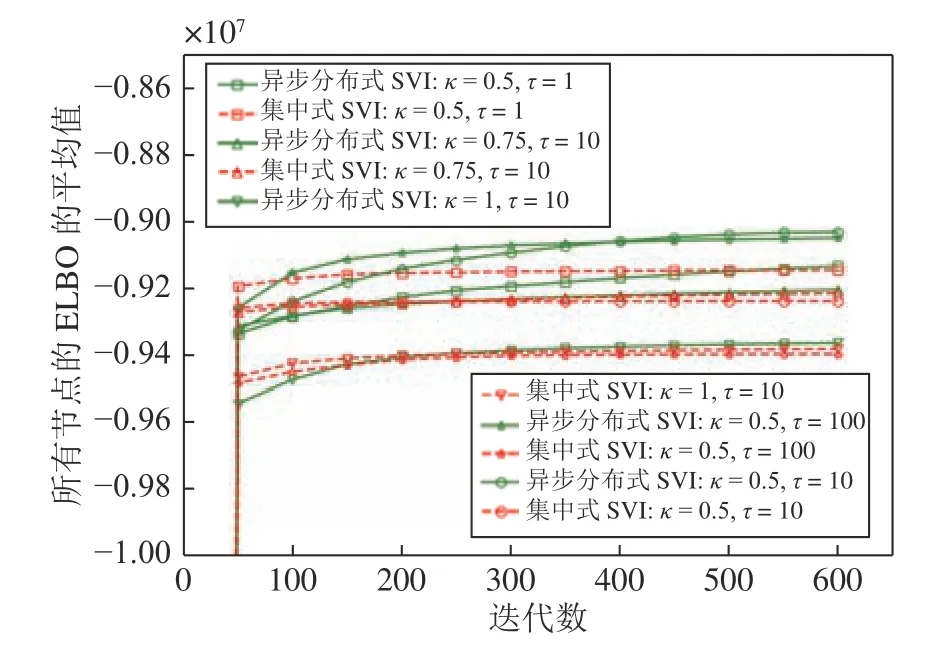
图5 不同 (κ,τ) 设置下异步分布式SVI 和集中式SVI 的ELBO 的平均值演化Fig.5 The evolution of the means of the ELBO for the asynchronous distributed SVI and the centralized SVI under different settings of (κ,τ)
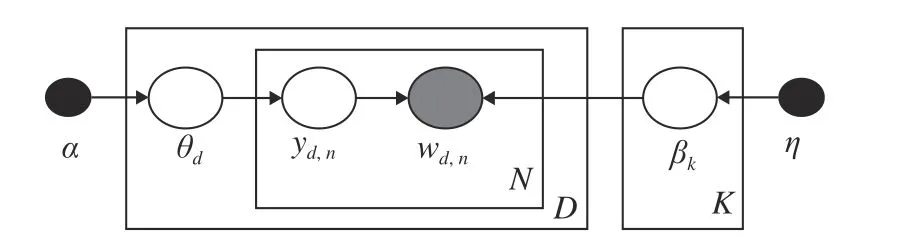
图6 LDA 模型的贝叶斯网络结构图Fig.6 The Bayesian graphic model of LDA
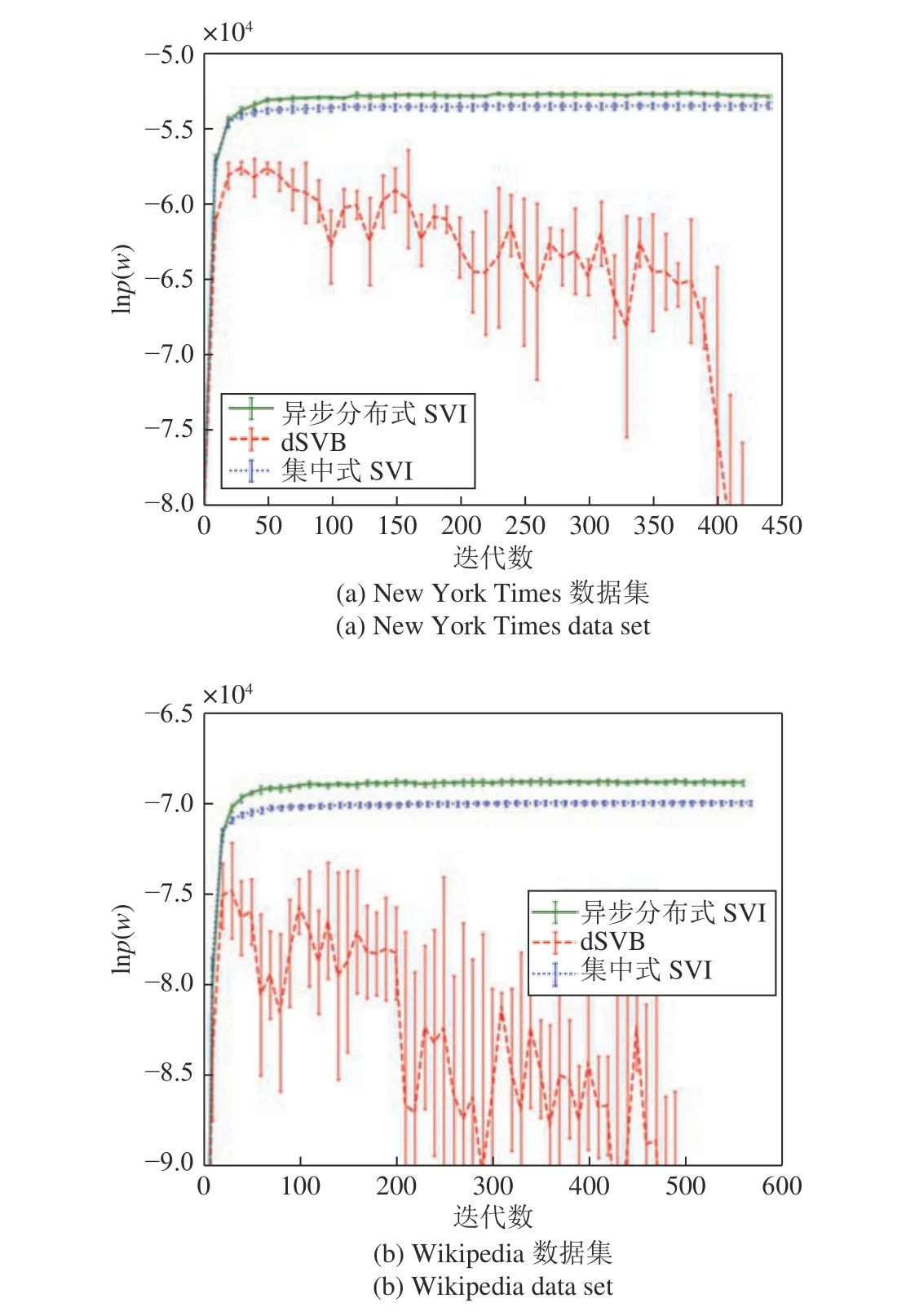
图7 异步分布式SVI、集中式SVI 和dSVB 在两个数据集上的表现Fig.7 Performance of the asynchronous distributed SVI,the centralized SVI,and the dSVB on the two data sets

表1 LDA 模型变量Table 1 Variables in LDA model

表2 不同参数设置下异步分布式SVI 和集中式SVI 收敛的值Table 2 The convergent values of the asynchronous distributed SVI and the centralized SVI under different parameter settings
然后我们在复旦大学中文文本分类数据集上测试所提出的异步分布式SVI 算法.该数据集来自复旦大学计算机信息与技术系国际数据库中心自然语言处理小组,其由分属20 个类别的9 804 篇文档构成,其中20 个类别的标签分别为Art、Literature、Education、Philosophy、History、Space、Energy、Electronics、Communication、Computer、Mine、Transport、Environment、Agriculture、Economy、Law、Medical、Military、Politics 和Sports.在预处理步骤中,我们首先去除了文本中的数字和英文并用语言技术平台(Language technology plantform,LTP)的分词模型对文本进行分词处理.为了减小训练的数据量,我们只读取每个类别的前100 篇文档进行训练.图8 展示了在K=20,α=0.2,η=0.2,κ=0.5,τ=10,分布式算法Batch size(批大小)取2,集中式算法batch size 取100 的设置下,异步分布式SVI 和集中式SVI 分别在复旦大学中文文本分类数据集上运行多次得到的lnp(w)的演化曲线,可以看到异步分布式SVI 收敛速度慢于集中式SVI,但是最终得到的 lnp(w) 值优于集中式SVI.
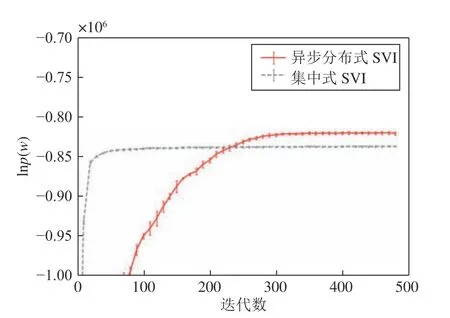
图8 异步分布式SVI 和集中式SVI 在复旦大学中文文本分类数据集上的表现Fig.8 Performance of the asynchronous distributed SVI and the centralized SVI on the Chinese text classification data set of Fudan University
图9 展示了在表3 所示的超参数组合设置下异步分布式SVI 和集中式SVI 在复旦大学中文文本分类数据集上训练100 个epoch 得到的 lnp(w) 的值的对比,其中横坐标为集中式SVI 得到的lnp(w)的值,纵坐标为对应超参数设置下异步分布式SVI 得到的 lnp(w) 的值.可以看到大部分数据点都位于左上方,表明大部分情况下异步分布式SVI都优于集中式SVI.并且注意到当batch size 取1 时异步分布式SVI 表现最差,在(κ=0.5,τ=1,batchsize=1)的设置下其表现不如集中式SVI.我们认为这是由于当batch size 太小时,分布式SVI的收敛速度过慢造成的.
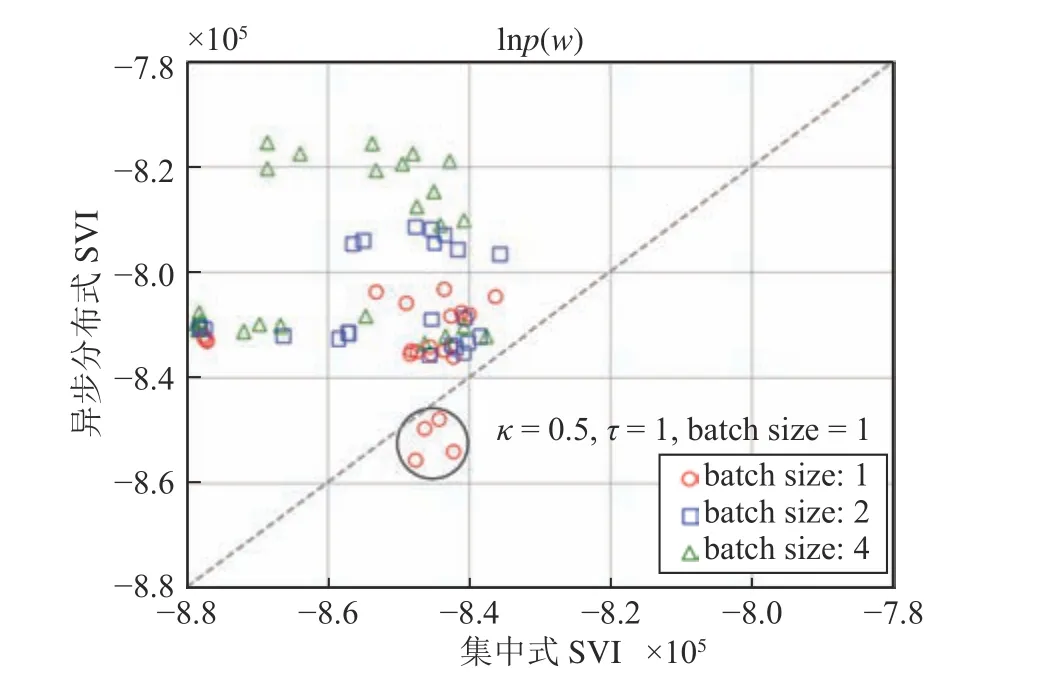
图9 不同超参数设置下异步分布式SVI 和集中式SVI 在复旦大学中文文本分类数据集上表现Fig.9 Performance of the asynchronous distributed SVI and the centralized SVI on the Chinese text classification data set of Fudan University under different hyperparameter settings
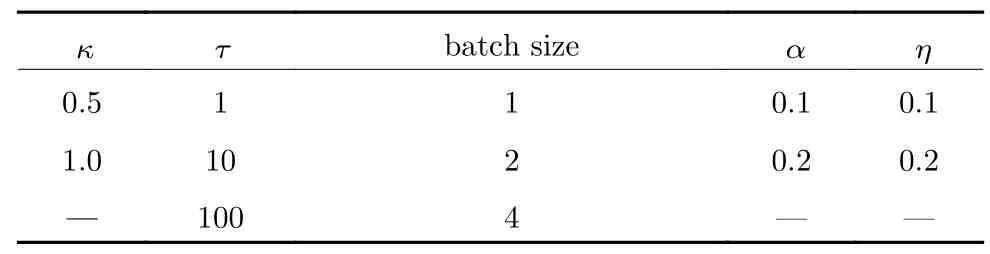
表3 超参数取值表Table 3 The values of hyperparameters
4 结论
本文针对无中心的分布式网络,基于扩散方法提出了一种新颖的分布式SVI 算法,其中采用自然梯度法进行本地更新以及采用对称双随机矩阵作为信息融合系数,并且为其设计了一种针对异步网络的适应机制.然后将其应用于BMM 和LDA 主题模型.在不同数据集上的实验均表明所提出的算法确实适用于异步分布式网络,而且其在发现聚类模式和对抗浅的局部最优方面的表现优于集中式SVI算法.
