水平管道负压气力输送CFD-DEM数值模拟
2021-03-04崔益华
崔益华
南通润邦重机有限公司
1 引言
气力卸船机作为负压气力输送设备,因其具有输送系统封闭、扬尘污染小、清仓彻底、构造简单紧凑、维护成本低等优点,被广泛应用于港口吸卸水泥、粉煤灰、矿石粉、化肥、粮食等散装物料。但气力卸船机的单位输送能耗远高于一般机械输送设备,无形中增加了卸船的运营成本。研究表明,气力卸船机80%以上的能耗来源于输送管道[1-2],因此管道系统的合理设计,对于整台机器的平稳运行和节能降耗意义重大。
在垂直管道气力输送过程中,物料颗粒所受重力方向与空气动力方向在同一竖直线上,因此只要用稍高于颗粒悬浮速度的气流速度,即可将物料颗粒顺利输送。然而在水平管道气力输送过程中,气流方向与重力方向垂直,物料易在管底沉积。因此要求水平管道具有比垂直管道更高的气流速度。而且在同一管道输送系统中,物料往往更容易在水平管道内发生堵塞。对于水平管道输送,通常存在一个保证颗粒平稳输送的安全速度,如果输送速度过高,虽然能安全输送物料,但系统的压力损失和功率消耗也会相应增大;如果输送速度比安全速度低,则颗粒很容易在管底堆积,形成脉动流,此时压力也会急剧增高,很容易造成管道堵塞。因此,合理地选择水平管道输送风速,对于气力输送系统的平稳运行至关重要。
以往的输送风速往往依靠试验或者实践经验确定。近年来随着计算机技术的发展,数值模拟作为试验的重要补充手段已被广泛应用于气力输送研究。目前的数值模拟方法主要分为两大类,一类是基于欧拉-欧拉法的双流体模型[3-6],其中流体相和颗粒相被视为可相互穿透的连续介质,两相分别在欧拉坐标系下求解动量方程和连续方程,通过引入体积分数使方程封闭;另一类是基于欧拉-拉格朗日法的颗粒轨迹模型[7-10],连续相在欧拉坐标系下进行描述,离散相则在拉格朗日坐标下进行颗粒轨迹求解。相较于双流体模型,颗粒轨迹模型能够记录每个颗粒的轨迹信息和动量信息,且对颗粒形状和受力把握更加精准,因此计算成本也更高。得益于现有工作站强大的运算能力,本文采用基于颗粒轨迹模型的CFD-DEM(计算流体力学-离散单元法)耦合方法,对不同直径下的水平管道输送玉米进行仿真,研究在相同的空气流量和物料流量下,不同管道直径对输送压损和物料流动形态的影响,以期为气力卸船机管道设计提供参考。
2 理论介绍
基于CFD-DEM耦合方法,连续相采用RNGk-ε湍流模型,颗粒相采用基于牛顿运动定律的离散模型。
2.1 连续相控制方程
气体作为连续相满足连续方程和动量守恒方程。气相连续方程为:
(1)
动量守恒方程为:
(2)
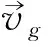
(3)
RNGk-ε模型中的湍动能k和湍动能耗散率ε,由式(4)确定:
(4)
(5)
式中,Cε1和Cε2的默认值为1.42和1.68;Gk为平均速度梯度引起的湍动能;αk和αε分别为k和ε的有效普朗特数的倒数;μe为气体有效粘度。
2.2 离散相控制方程
颗粒相作为离散相遵从牛顿第二定律,将颗粒运动分解为移动和转动,控制方程分别描述为:
(6)
(7)
式中,mp、vp、Ip和ωp分别为颗粒质量、平移速度、转动惯量和角速度;Fw-p、Fp-p和Mp分别为壁面对颗粒的力、颗粒之间作用力和颗粒所受力矩;Ff为流体对颗粒的作用力,包括曳力、上浮力、巴塞特升力、萨夫曼升力、马格纳斯升力等。当颗粒密度与流体密度相差较大时,曳力起主要作用,因此将曳力视为Ff。
2.3 连续相与离散相相互作用
根据式(2)和式(6),连续相与离散相之间通过动量交换实现耦合:
(8)
式中,Kgs为动量交换系数,本文采用Gidaspow等[11]给出的公式:
(9)
式中,ds为颗粒当量粒径;CD为与颗粒雷诺数ReS相关的阻力系数。其中:
CD=
(10)
颗粒雷诺数定义为:
(11)
3 数值模拟设置
3.1 计算模型及网格划分
选取长度为15 m,管道直径D分别为230 mm、280 mm、320 mm、350 mm、380 mm和430 mm水平管道进行仿真对比。采用六面体结构化网格对流体域进行网格划分。其中直径为320 mm的管道几何模型和网格划分见图1。

图1 水平管道几何模型和六面体网格划分
3.2 物性参数及边界条件设置
以往采用CFD-DEM耦合方法对气力输送的研究大多集中于稀相气力输送[12],因颗粒数较少,可忽略颗粒体积分数对流场的影响。管道输送颗粒数量庞大,颗粒体积分数会对流场产生显著影响,因此采用双向耦合的方式进行,并充分考虑颗粒体积分数对流场的影响。
由于计算颗粒数量庞大,模拟中采用简化的双球颗粒代替玉米颗粒(见图2)。管道边界条件见图3,相对环境压力为-25 000 Pa,绝对压力为76 325 Pa,采用质量入口边界条件,压力出口边界条件,壁面为无滑移边界条件。入口空气质量流量为2.38 kg/s,出口压力为0。颗粒生成速率为41.67 kg/s(约150 t/h)。入口空气密度为:
(12)
式中,ρ0为常温标准大气压下的空气密度,取1.225 kg/m3;P0为常温下的标准大气压,取101 325 Pa;P为环境绝对压力,取76 325 Pa。物性参数及边界条件设置见表1。

图3 水平管道输送边界条件
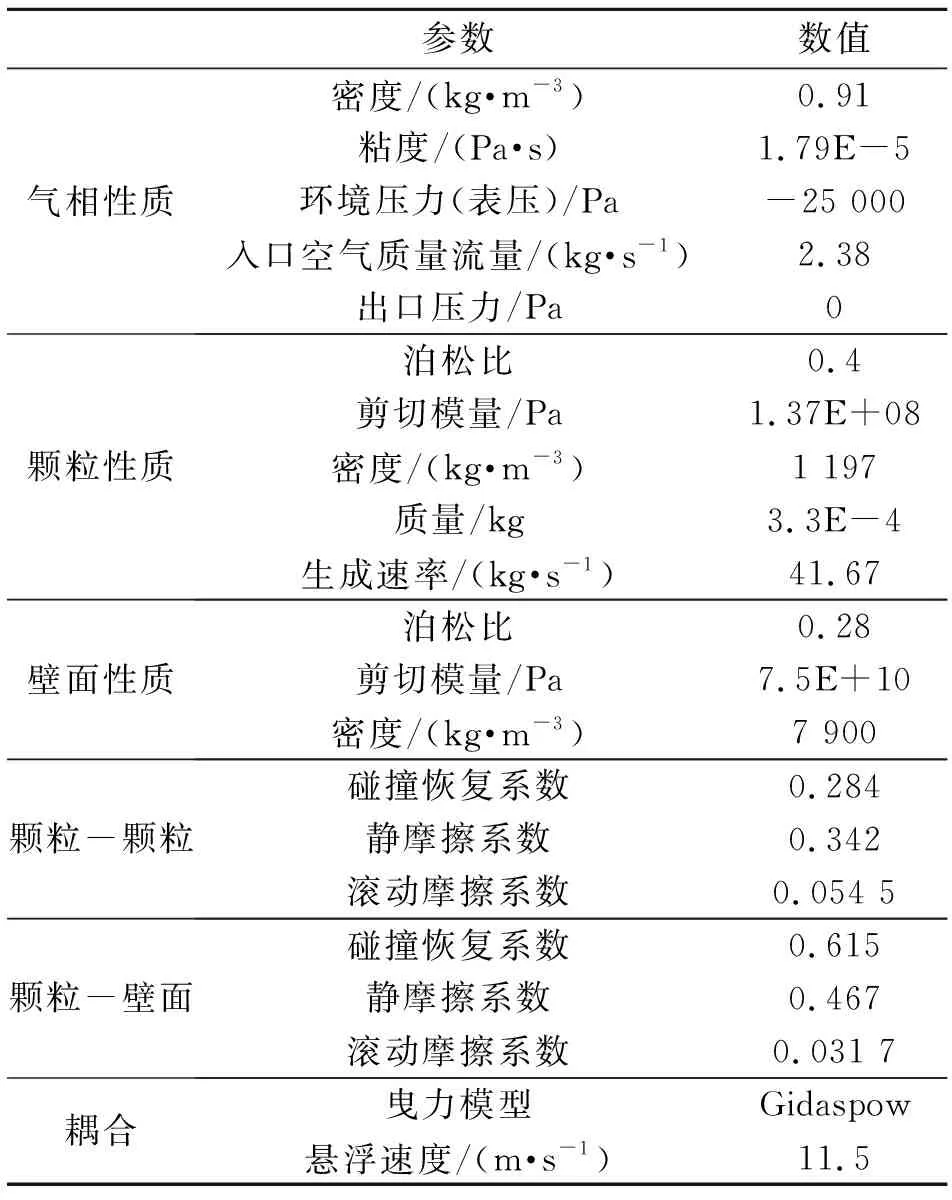
表1 物性参数及边界条件设置
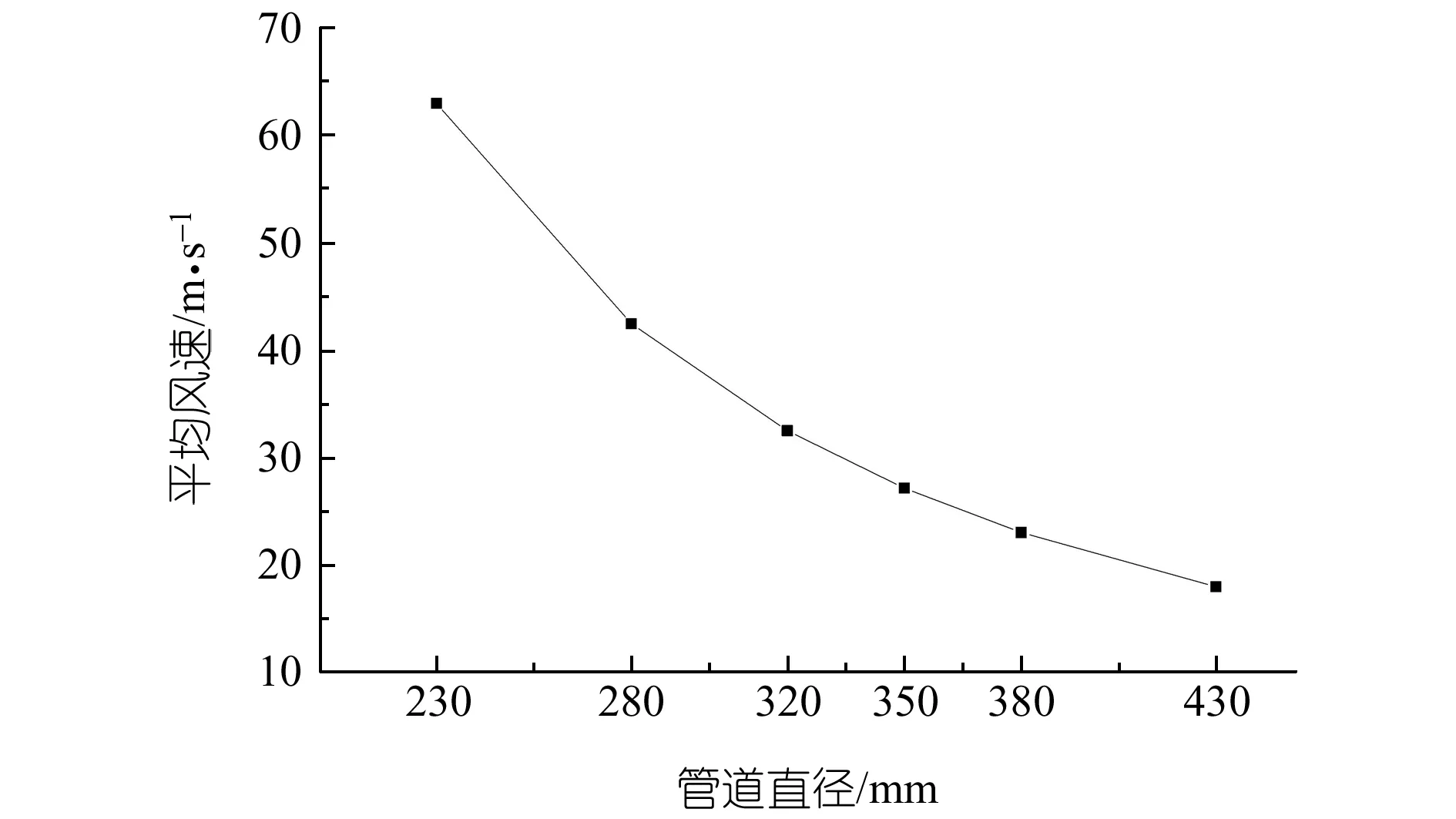
图4 不同直径管道平均风速变化
4 仿真结果对比及讨论
4.1 颗粒流动特性分析
气流速度会对颗粒流动特性产生显著影响。在入口空气质量流量相同的情况下,平均风速随管道直径增加而降低(见图4)。图5为9 s时刻物料颗粒在不同直径管道内分布情况,可以看出,由于管道直径的增加,管道内平均风速不断降低,物料颗粒在管道内由半悬浮流动状态到全部管底流动状态再逐渐过渡到沙丘流动状态。考察物料堆积处管道截面颗粒分布,可以很清楚地看出,管道底部颗粒数随管道直径增加逐渐增多(见图6)。在230 mm管道内大部分颗粒呈悬浮状,管底颗粒运动速度已接近20 m/s;在280 mm管道内颗粒悬浮数量明显减少且颗粒运动速度也有所降低;在320 mm管道内颗粒全部沉积于管底并以5 m/s左右的速度向前运动;当管道直径达到350 mm以上时,管底颗粒速度几乎为零,此时颗粒在管底大量堆积,且堆积量随着管道直径增加而增加,并有堵塞管道的趋势。

图5 不同直径管道颗粒分布,t=9 s
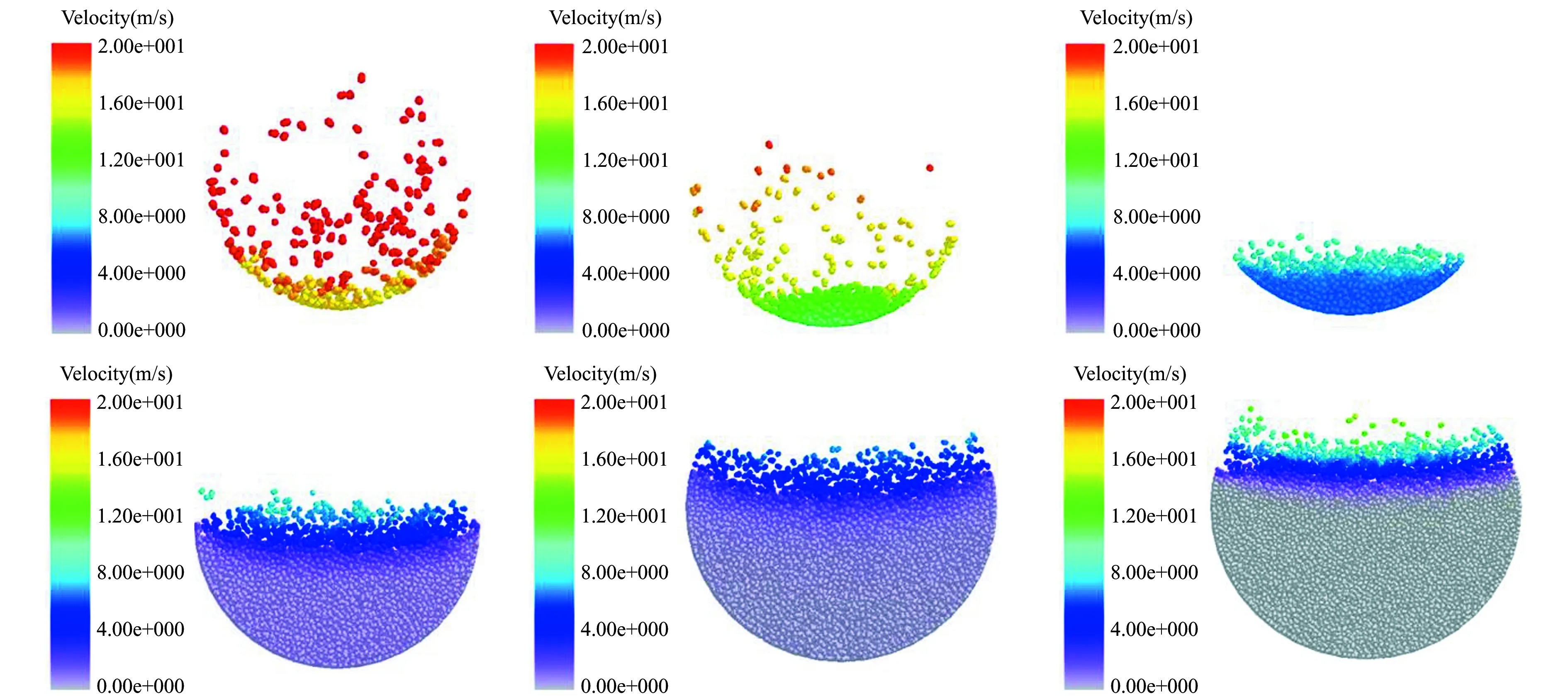
图6 不同直径管道截面颗粒分布,t=9 s
考察380 mm管道内颗粒堆积过程,由于气流速度不足,大部分物料颗粒停滞在管道底部(见图7)。随着颗粒在管道底部不断积聚,管道断面面积逐渐变小,使得该区域上部气流速度明显增大(见图8),料堆表面一层颗粒被气流吹散,当沉积颗粒与吹散的颗粒平衡时,在此处形成固定料堆。由于料堆的存在,此处断面面积突然减小,相当于管道突然缩颈,造成此处压力损失突然增大。从图9也可以看出,管道压力分布梯度在堆积处明显增大,表明在此处压损较大。
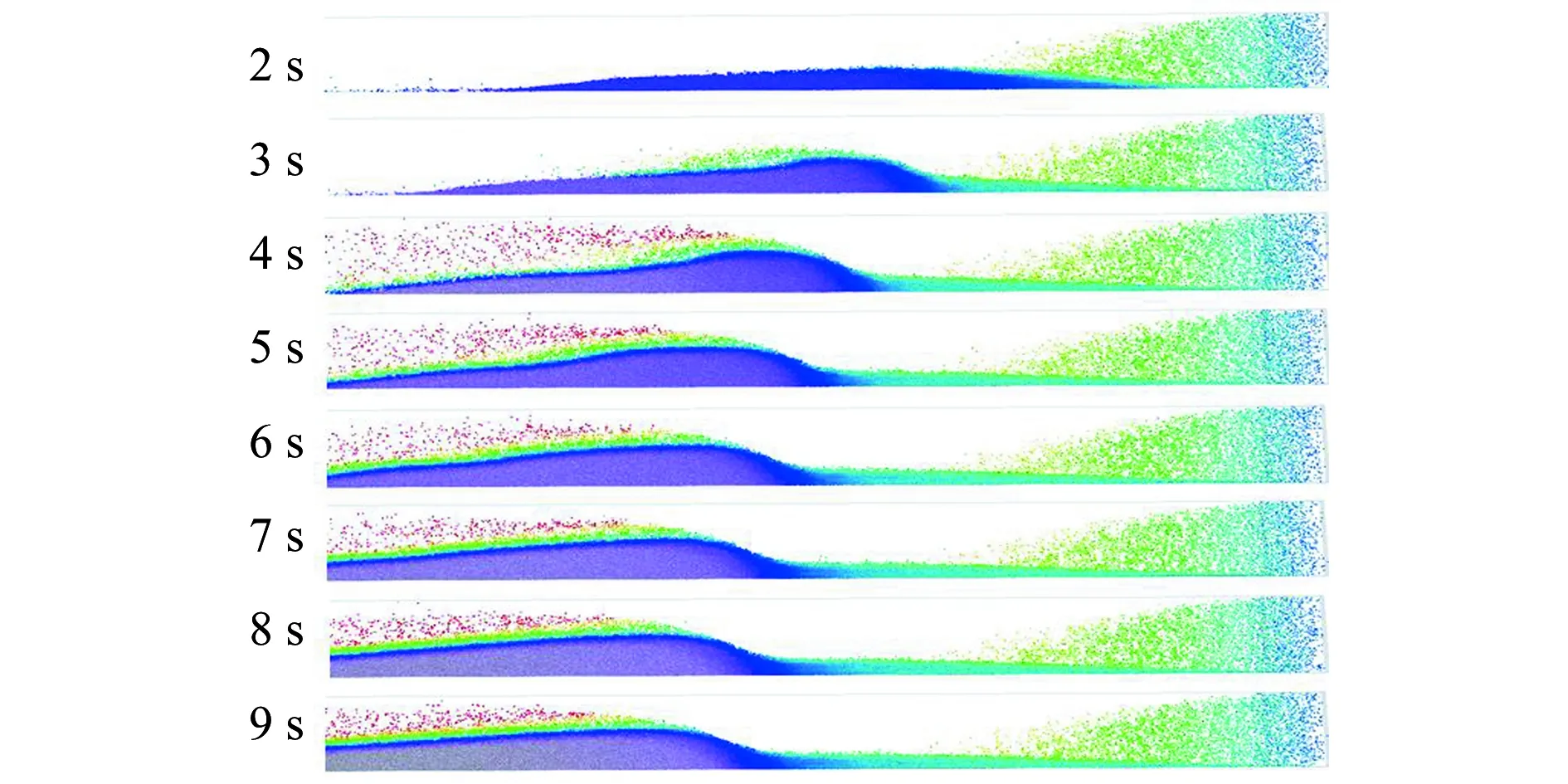
图7 380 mm直径管道内颗粒堆积过程
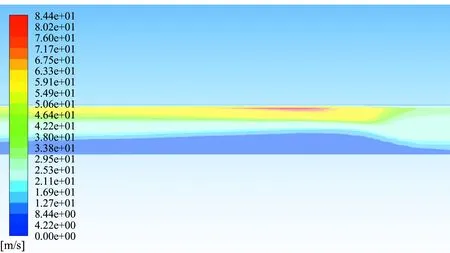
图8 380 mm直径管道堆积处气流速度分布
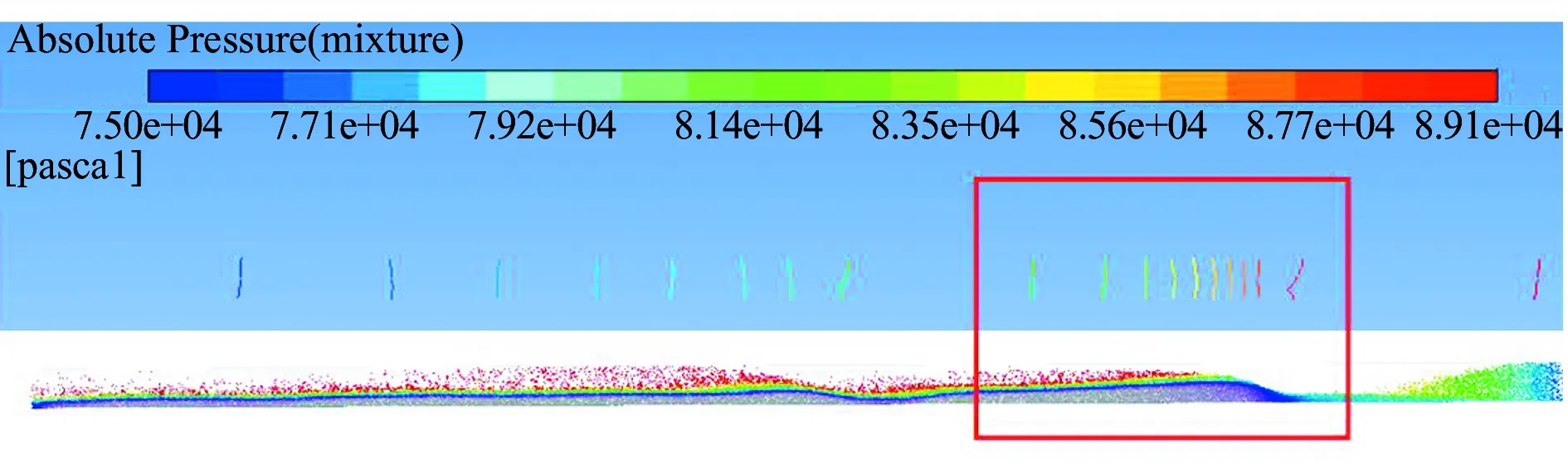
图9 380 mm直径管道内压力变化
4.2 管道压损对比
因物料颗粒在不同直径管道内流动形态不同,在相同空气流量和物料流量条件下,管道压损差异较大。通过对比不同直径管道压损随时间变化,可以看出230 mm管道、280 mm管道和320 mm管道分别在1.3 s时刻、1.8 s时刻和2.4 s时刻压损达到稳定,350 mm管道、380 mm管道和430 mm管道压损则持续上升(见图10)。
对比3 s时刻和9 s时刻不同直径管道压损(见图11),3 s时刻管道内颗粒堆积没有形成规模,管道压损随管道直径增大逐渐减小;然而经过一段时间后的9 s时刻,管道压损随管道直径增加呈先减小后增加的趋势,且在管道直径为320 mm时压损最小。当管道直径在320 mm以下时,管道内颗粒未持续堆积,此时管道压损与3 s时刻相同,且管道直径越大压损越小;当管道直径超过320 mm时,则因颗粒在管道底部逐渐堆积,管道压损相较于3 s时刻明显增大,且压损随管道直径增大逐渐增大,可见颗粒在管道内堆积会对管道压损产生显著影响。
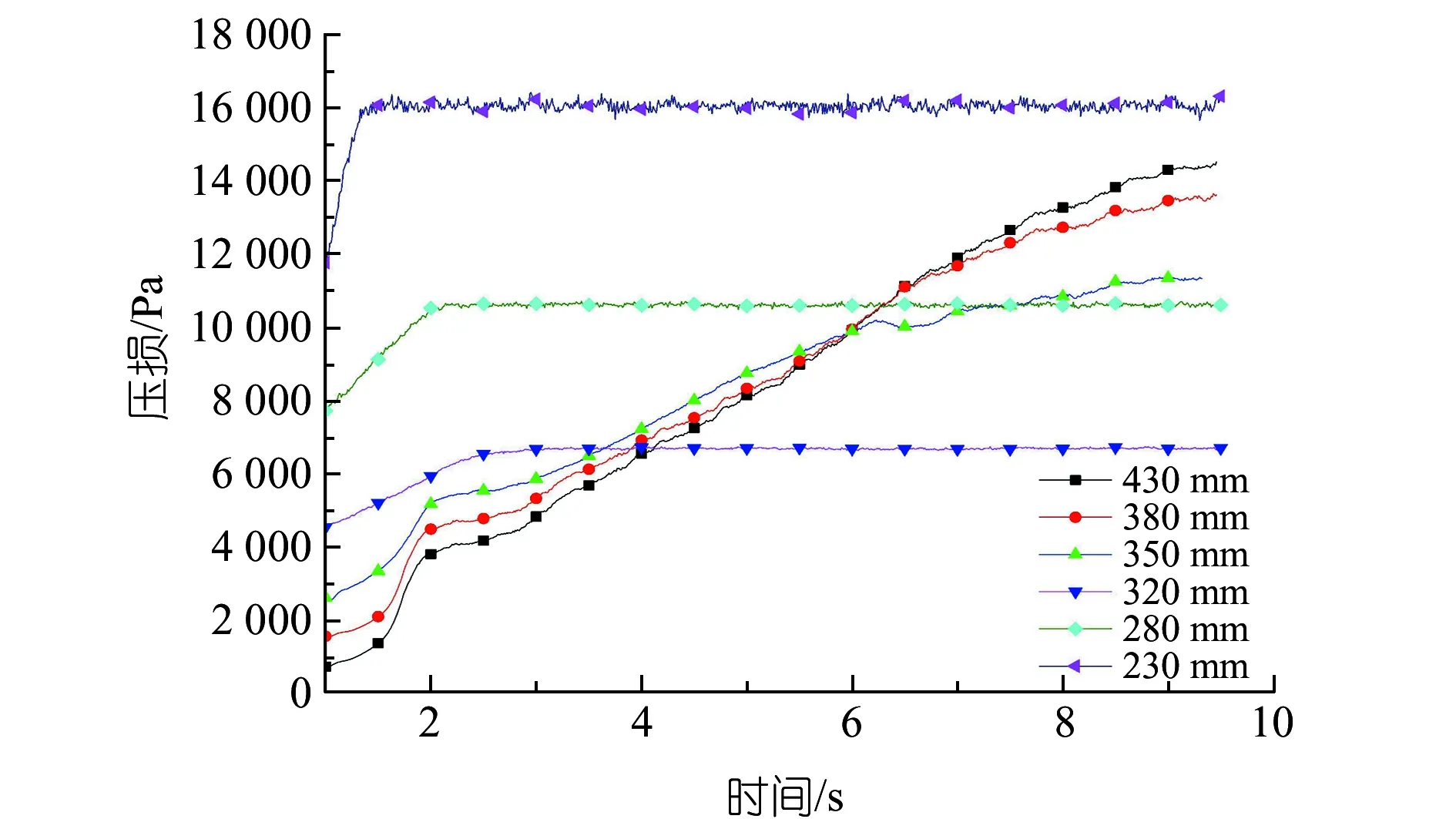
图10 不同直径管道压损随时间变化

图11 3 s时刻和9 s时刻不同直径管道压损对比
5 结语
采用基于颗粒轨迹模型的CFD-DEM方法对负压气力输送系统中的水平管道进行仿真研究,仿真过程中充分考虑颗粒体积分数对流体的影响。通过对比不同直径管道在相同空气流量和物料流量下的流动特性和压力损失发现,管道直径在320 mm时压力损失最小。以320 mm管道为分界点,在直径小于等于320 mm输送管道内,颗粒表现出稳定的悬浮管底流动形态,且压力损失随管道直径增加而减小;但当管道直径大于320 mm时,颗粒因在管底大量滞留而表现为沙丘状流动形态,此时压力损失随管道直径增加而增大。因此,在负压气力输送系统中,水平管道直径的选取应遵循的原则是:在确保物料颗粒处于管底流动形态下尽量增大管道直径,从而使系统在最小压损下顺利输送物料。
