基于迭代学习控制的划片机高精度运动误差补偿

王建新，郑 浩

（1.沈阳工业大学人工智能学院，沈阳110870；2.沈阳仪表科学研究院有限公司，沈阳110043）

1 引 言

划片机作为电子元器件封装的关键设备，其系统稳定性、可靠性和加工精度对划切质量起到关键的作用。然而因种种现实因素的存在，在划片机加工过程中会产生许多不同种类的误差，比如在系统运动过程中由温度而造成的热变形误差、划片机床自身几何误差、动力学误差等等。这就对划片机的高精度运动误差补偿提出了更高要求。传统的误差补偿方法主要是采用机理建模或者辨识建模，拟合出一条离线线性曲线，但此法可能会造成较大的拟合误差，可实现性差。在此问题上，随后出现了采用数据驱动[1]中迭代学习控制的方法，来实现划片机运动误差补偿。

1984 年，日本学者有本卓[2]首次提出了迭代学习算法，之后便得到广泛应用。由于迭代学习控制算法无须建立精确的被控对象物理模型，仅仅通过输入输出数据就可完成控制系统的设计，解决了模型建模困难的问题。张洁洁[3]采用基于数据驱动的无模型自适应迭代误差补偿方法尝试解决传统问题的难点，虽然误差补偿的精度有所提升，但是随着迭代次数的增加无法保证系统收敛。孟婷婷[4]通过设计迭代学习控制器提高了系统的收敛性，但只能解决单轴的跟踪误差，无法达到多轴的运动控制误差补偿。梁建智[5]通过迭代学习算法将数控机床加工动力学过程转化为迭代数据模型，有效提升了加工精度。

2 迭代学习控制原理及神经网络

2.1 迭代学习控制

在处理系统运动控制任务时，往往要通过被控对象的实际运行轨迹与期望轨迹之间的差值进行调整，迭代学习正是利用这一原理，依靠前一次或前几次操作测得的误差信息来修正控制输入，通过不断重复，使得该重复任务在下一次操作时更加准确，最终达到整个时间区间上输出轨迹与期望轨迹的重合。

迭代学习控制[6]通过函数迭代方法来实现，即构造用于修正控制的学习律，使得它产生一个函数序列{uk(t)}，收敛于u(t)。迭代学习律的典型形式为：

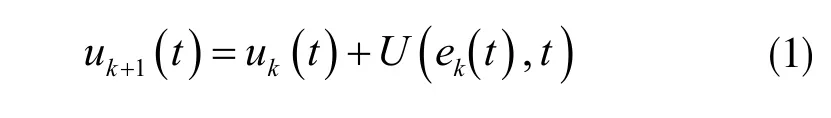
其中k=1,2,...N，代表周期数；uk+1(t)代表第k+1 次操作时的操作输入；uk(t)表示当前操作使用的输入，ek(t)=yd(t)-yp(t)，表示当前操作误差；U(uk(t),t)表示当前所得到的误差学习方式。学习律常用表现形式有如下两种：

D 型学习律：

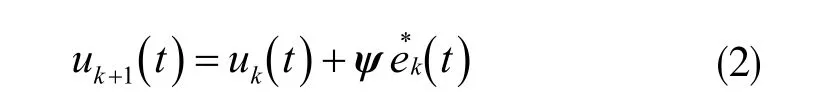
P 型学习律：

其中, ek(t)表示误差，φ 表示定常增益矩阵。

为保证系统训练的稳定性，迭代学习具有相同的初始状态，常见的初始条件有：

①迭代初态与期望初态一致，即xk(0)=xd(0)（,k=1,2,...），称作初始状态严格重复；

②迭代初始状态固定；

2.2 神经网络

神经网络是由多个神经元按照一定规则连接起来所构成，主要包括输入层、隐藏层、输出层，结构图如图1 所示。其中，输入层负责接收输入数据；输出层负责获取神经网络输出数据；隐藏层位于输入层和输出层之间，外部不可见。神经网络的结构类型有很多，比如：卷积神经网络、循环神经网络等。此处选用BP（Back Propagation）神经网络结构。

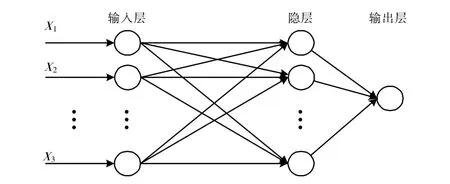
图1 神经网络结构图

3 系统设计

3.1 划片机系统结构

本设计中划片机系统的控制器采用三环控制结构，分别为电流环、速度环、位置环。三环控制结构框图如图2 所示[7]。I(s)、V(s)、P(s)分别表示电流环控制器、速度环控制器、位置环控制器。E(s)、M(s)分别代表电力系统和机械系统。

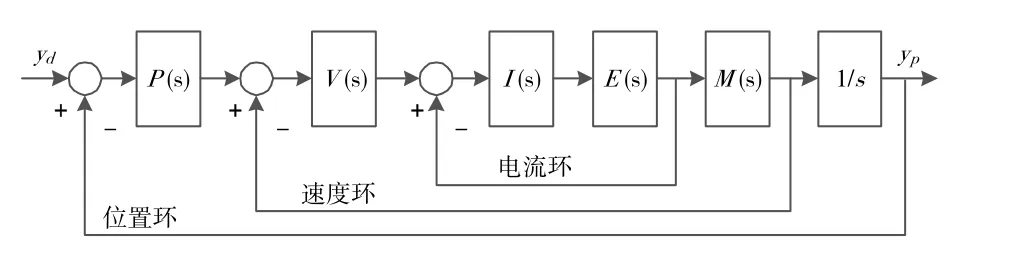
图2 划片机系统三环结构图

此处所采用的迭代学习控制算法不需要建立精确模型，仅需系统运动过程中产生的输入输出数据不断迭代即可达到误差补偿，所以仅仅需要位置环，将速度环和电流环以及被控对象整体封装成一个新的被控对象。通过对位置环参数的调整，形成一个新的控制系统。

3.2 划片机迭代控制系统设计

划片机运动控制系统[8]采用迭代学习控制算法的目标是能够精确地跟踪参考轨迹从而达到高精度定位。跟踪误差ep(k)=yd(k)-yp(k)尽可能接近0（其中yd(k)表示期望轨迹，yp(k)表示实际轨迹）。此处的算法是通过系统输入输出数据实现的，所以设计一个误差补偿环路，不需要对误差进行建模，从系统的输出位置得到实际的运行轨迹。误差补偿[9]迭代控制过程如图3 所示。控制律结构如图4 所示。

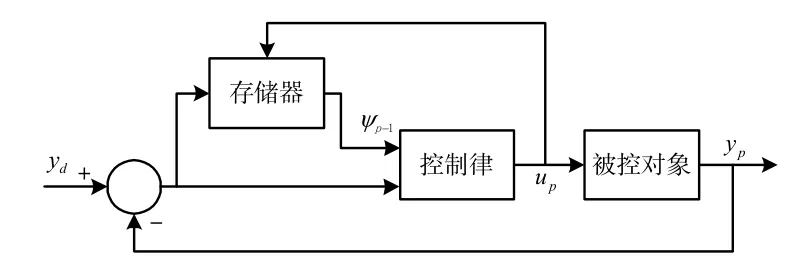
图3 误差补偿迭代控制框图

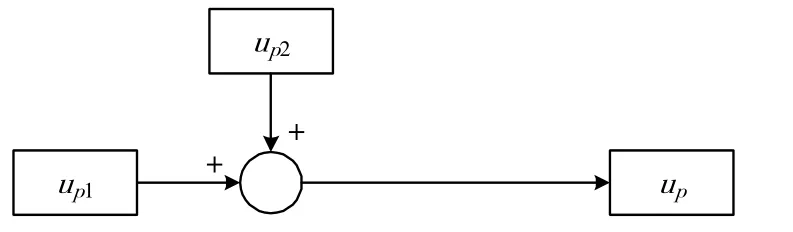
图4 控制律结构框图

图4 中，up(k)=up1(k)+up2(k)。其中up1(k)表示迭代学习控制器，它的表现形式为：

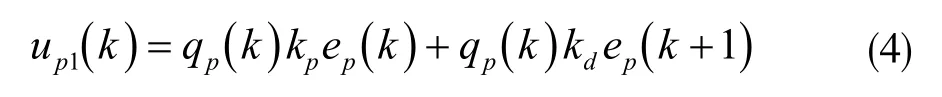
式中，qp(k)∈{0,1}，当qp(k)=0 表示数据缺失；qp(k)=1则表示没有缺失。kp为比例因子，kd表示微分因子。当kd=0，为P 型控制律；当kp=0，为D 型控制律；当kp≠0 且kd≠0，则为PD 型控制律。

up2(k)为迭代神经网络控制器，它的表现形式为：

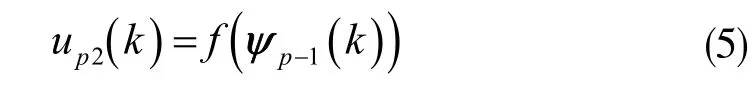
式中，f 表示非线性函数；ψp-1(k)表示p-1 时刻的向量，它的形式决定着控制器的结构，规则如下：

P 型控制律：

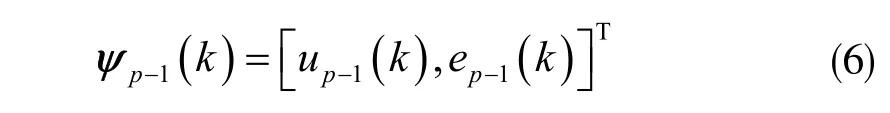
D 型控制律：

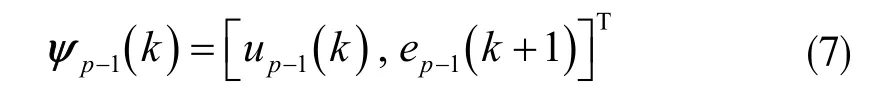
PD 型控制律：

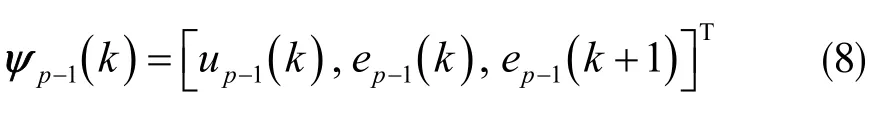
控制系统的目的是经过多次重复试验找到一个非线性函数f，实现尽可能最小的轨迹误差[10]。为降低建模误差对参数优化过程的影响，同时提高算法的跟踪性能，在此选择传统PD 型控制律与神经网络结合设计PD 神经网络迭代控制器。神经网络有很好的泛化性，能够提高系统的控制性能。采用的神经网络为全连接层，形式为：

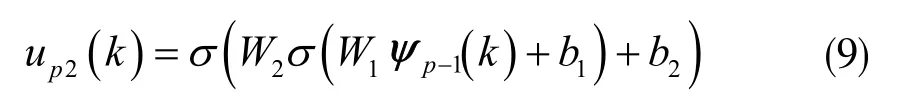
式中，W1、W2、b1、b2分别为输入层到隐藏层、隐藏层到输出层的权重和偏差。σ 为隐藏层和输出层的激活函数。公式(9)主要依赖迭代控制器Ψp-1(k)向量以前的重复实验所决定。

4 仿真结果与分析

为验证划片机迭代控制系统有效性，给定划片机运动控制系统跟踪期望轨迹为yd(t)=sin(t)。划片机位置伺服系统采样步长为0.01，仿真时间为10 s，迭代次数为30 次。

首先对简单的P 型控制律迭代控制进行仿真分析，仿真结果如图5 所示。

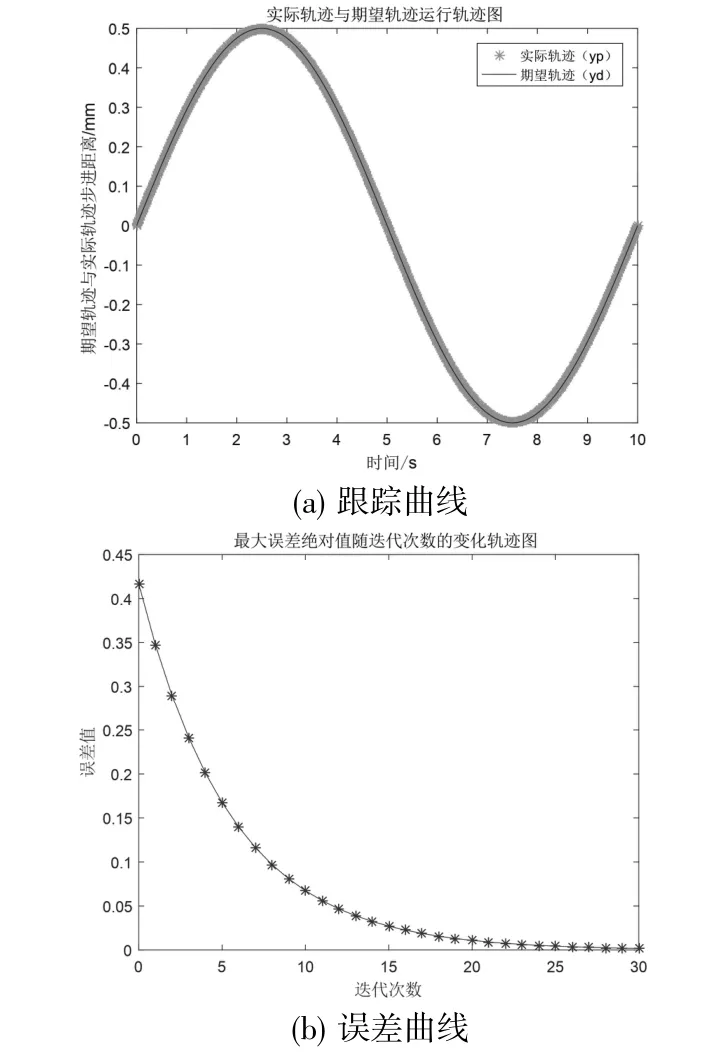
图5 P 型控制律迭代控制仿真结果

由图5(a)可见，随着迭代次数的增加，实际轨迹逐渐逼近期望轨迹;从图5(b)可以看出随着运行次数的增加，系统的跟踪误差越来越小，并趋于稳定。

然后对PD 型控制律迭代控制进行仿真分析，结果如图6 所示。

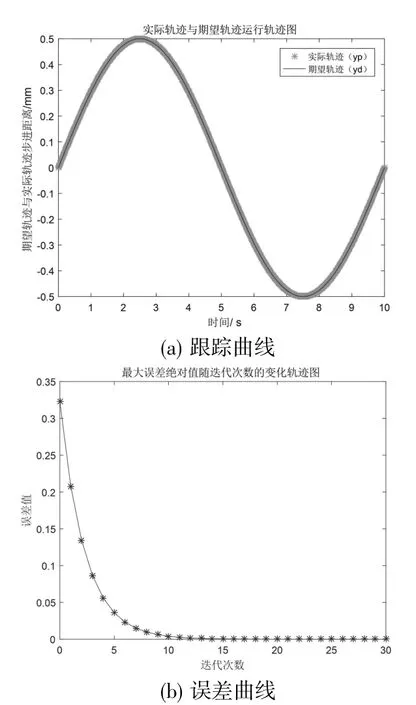
图6 PD 型控制律迭代控制仿真结果

从图6(a)中可看出，随着迭代次数增加，实际轨迹已经跟踪上期望轨迹，但是收敛速度不够快;从图6(b)可见控制系统运动的跟踪误差已经很小了。

最后对迭代神经网络控制律进行仿真分析，仿真结果如图7 所示。从图7(a)可以看出实际轨迹很好地跟踪上了期望轨迹；从图7(b)可见，跟踪误差随着迭代次数增加逐渐变小，并且收敛速度变快。

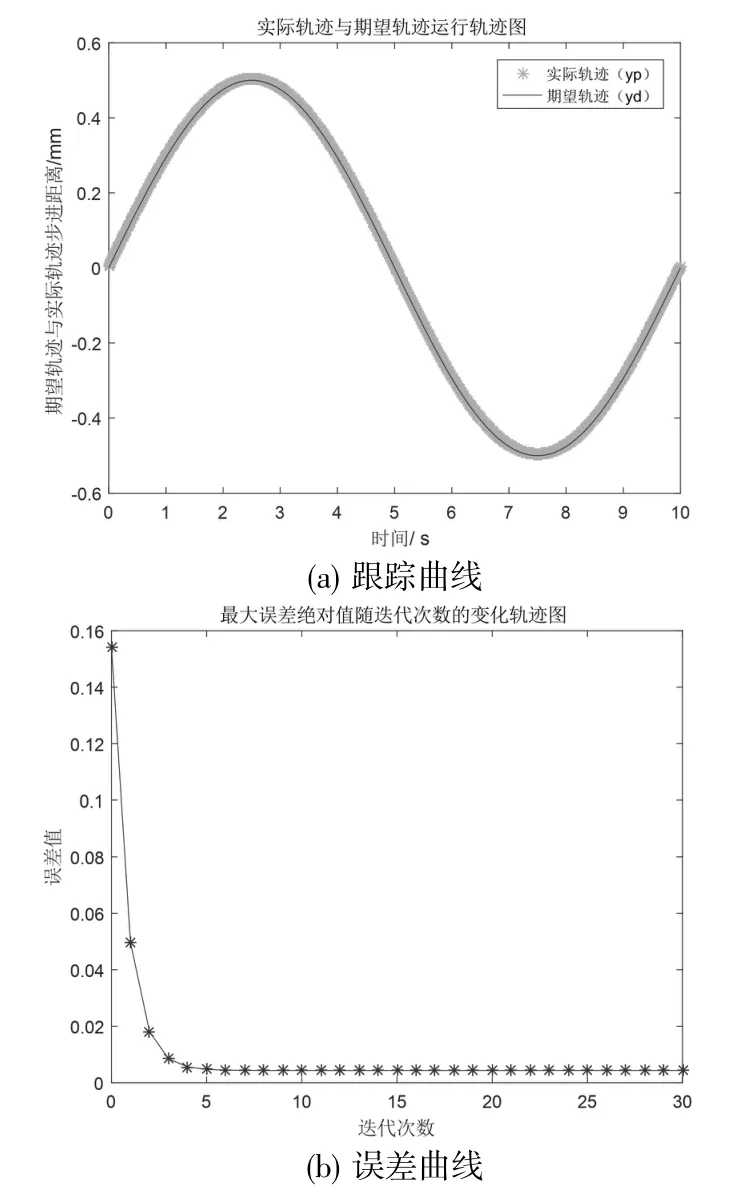
图7 神经网络控制律迭代控制仿真结果

从仿真结果可见，随着迭代次数的变化，在跟踪误差方面，迭代学习神经网络控制方法明显优于P型、PD 型迭代学习控制法。此外，迭代学习控制神经网络的权重和偏差增益是迭代式变化，而P 型和PD 型迭代学习控制的控制增益是固定不变的，就决定了迭代学习控制神经网络每次迭代能寻找到更优化的控制，具有更快的收敛性，控制精度也得到提高，有效实现了划片机运动轴的误差补偿。

5 结 束 语

在对划片机运动控制伺服系统分析的基础之上，利用迭代学习神经网络算法完成了划片机误差补偿控制系统的设计。分别对于P 型、PD 型控制律以及神经网络迭代控制进行仿真分析，验证了采用迭代学习控制神经网络方法能够有效的提高控制精度，该设计对系统的各轴运动控制都具有同样适用性，在实际使用中能够有效提高工作效率。