小样本条件下的血糖浓度预测算法研究*

黄雄波，丘 陵，刘武萍

（1.佛山职业技术学院电子信息学院，广东 佛山528137；2.佛山市中医院药剂科，广东 佛山528000）

1 引 言

正常来说，人体自身的血糖调整机制可将其体内的血糖值维持在正常范围以内。然而，由于胰岛素分泌缺陷或其生物作用受损，或两者兼有所引起的糖、脂肪和蛋白质代谢障碍，往往会促进人体内的血糖值升高，并导致糖尿病的发生[1-2]。研究表明，高血糖对人体的危害非常大，会给人体造成严重的疾病以及负面影响，例如急性心肌梗塞、中风、重症感染、败血症、感染性休克、多发性精神病、多器官衰竭等等，严重的甚至会导致死亡。按照发病机理的不同，糖尿病可以分为I 型糖尿病和II 型糖尿病两种。其中I 型糖尿病是由于感染（尤其是病毒感染）、毒物等因素诱发机体产生异常的细胞免疫应答，导致胰岛β 细胞损伤，胰岛素分泌减少而引起的；II 型糖尿病是由于致病因子的存在，正常的血液结构平衡被破坏，血中胰岛素效力相对减弱，并经过漫长的病理过程而形成的[3-5]。

注射胰岛素是糖尿病患者维持正常血糖水平的重要手段。为了提升治疗效果，有必要对患者未来一段时间（一般为30 分钟）的血糖浓度进行精确的预测，以便确定注射胰岛素的最佳时间和剂量[6]。R.Hovorka 等通过非线性动力系统模拟皮下注射的短效胰岛素及肠道的吸收过程，并采用贝叶斯参数估计确定时变模型参数，得到一种有效的非线性血糖预测模型[7]。H.Efendic 等基于生理学与血糖变化的转移概率，使用高斯函数设计实现了区间概率的血糖浓度短期预测算法，该法对10耀30 分钟时间范围的血糖浓度有非常好的预测效果[8]。近年来，基于数据驱动的血糖浓度预测方法得到了长足的发展，利用机器学习和深度学习对既有的血糖序列进行特征提取、非线性映射等处理，其预测精度较基于生理模式的经典预测模型而言，有着不可比拟的优势[9-11]。鉴于现有的血糖浓度预测模型在小样本情形下仍有不足，在此设计并实现一种基于小样本的血糖浓度预测算法。改进后的算法将在保证一定预测精度的情况下，使得血糖序列的采样时间间隔从原来的5 分钟延长至3 小时。

2 血糖序列的预处理

受血糖检测设备或输入转换等原因的影响，所获得的血糖原始序列往往会混杂着少量的异常数据，若直接对这些原始序列进行建模处理，则可能会导致建模结果出现较大的误差。为此，需要对血糖原始序列进行相关的合理性检验，以剔除有明显偏差的不合理样本点。同时，为保证原始序列的完整性，应使用合理的数据替换被剔除的样本点。

对于异常样本点，常用的检测与剔除方法有拉依达准则、肖维勒准则、格拉布斯准则、狄克逊准则及t 检验准则等。其中，t 检验准则的计算过程较为复杂，但其检测结果更为严格和稳健。据此，此处采用t 检验准则对血糖原始序列展开检验。

记血糖原始序列为yt（t=1,2,...,n），按样本点的数值大小进行排序，有：

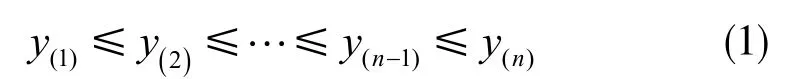
若有：

或

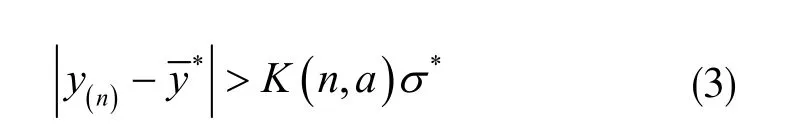
两式成立，则称y(1)或y(n)为异常数据，应予以剔除。

而K(n,a)则是对应样本容量n 与某一置信水平a，并结合t 分布临界值表计算得到的数值。

当检测发现异常样本点之后，则以该样本点为中心、邻域半径为2，选取左右相邻4 个样本点，依照Lagrange 插值原理[12]，析出对应的插值函数，在此基础上，得到异常样本点的合理替换值。Lagrange 插值原理具体如下：

设已知函数y=f(x)在区间[a,b]上n+1 个点x0,x1,...,xn所对应的值为y0,y1,...,yn，要求作一个次数不高于n 次的插值多项式Ln(x)，且满足插值条件：

于是，选取特定的基函数，并用这些基函数的线性组合来表示Ln(xi)，便可得到Lagrange 插值多项式:

3 血糖序列的样本扩充

由于既有的血糖序列是属于小样本的情形，为了提高辨识建模的精度，有必要进行相应的样本扩充处理。与上述的异常样本的插值替换处理不同，样本扩充的插值范围为整个样本取值区间。由于此时的插值函数需要满足更多的样本点，于是导致了插值多项式次数的增加，从而引起龙格（Runge）现象。为了获得更好的插值效果并同时增强插值函数的整体光滑度，此处采用分段的三次样条函数来完成样本扩充，即插值函数是由一段一段的三次多项式（二阶连续导数）拼合而成的曲线。

设在区间[a,b]上的插值节点a=x0＜x1＜...＜xn=b 与所对应的函数值分别为y0,y1,...,yn，若函数S(x)为三次样条插值函数，则下列3 个条件成立[13-14]：

条件1：S(x)=yi, i=0,1,...,n；

条件2：在每一个小区间[xi-1,xi]上是一个关于x的三次多项式；

使下式:

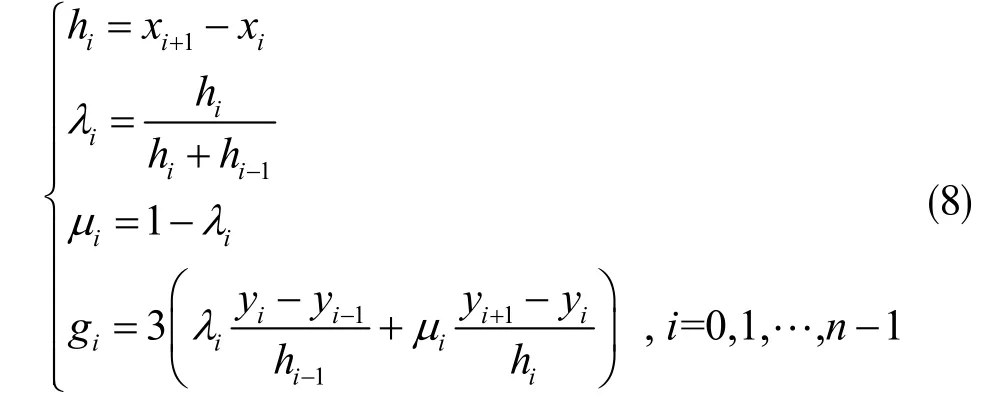
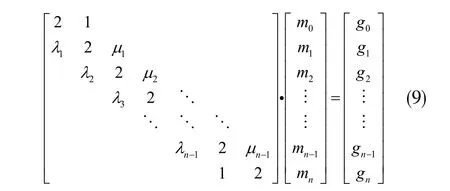
将原始的小样本血糖序列代入式(8)耀(10)，于是在相邻样本点[xi-1,xi]之间求得一个对应的三次样条插值函数Si(x)。根据实际需要，将[xi-1,xi]划分为n 等份，有[xi-1,xi-1+Δx,...,xi-1+(n-1)Δx,xi]，易知，将xi-1+φΔx（φ=0,1,...,n-1）代入Si(x)，便可完成样本插值的扩充处理。

4 血糖浓度的小样本预测

4.1 基于广义回归神经网络的血糖浓度预测

小样本血糖序列在剔除异常样本及样本扩充之后，便可进行预测模型的构建。注意到血糖序列本身具有的非线性和非平稳的特点，在此选用广义回归神经网络对小样本血糖序列进行预测。广义回归神经网络是属于径向基神经网络的一种改进，具有很强的非线性映射能力及高度的容错性，特别是在小样本的情形下，其逼近能力和学习收敛速度比径向基神经网络具有更优越的性能[15-16]。

基于广义回归神经网络的小样本血糖浓度预测模型的构成如图1 所示。其中包括输入层、模式层、求和层和输出层，其网络输入X= [x1x2...xn]T，而网络输出Y=yi,i=0,1,...,m。

图1 预测模型构成示意图

如图1 可见，输入层的神经元数目等于待预测血糖浓度序列点的前p 个连续的样本；模式层的神经元数目与学习样本的数目n 相等，该层的每个神经元的传递函数如下式所示：

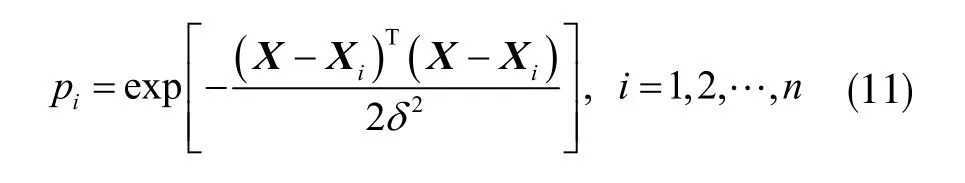
式中，X 为输入变量，Xi为第i 个神经元对应的学习样本，σ 为光滑因子，即高斯函数的标准差。

求和层用于对所有模式层神经元的输出进行算术求和及加权求和，如下式所示：

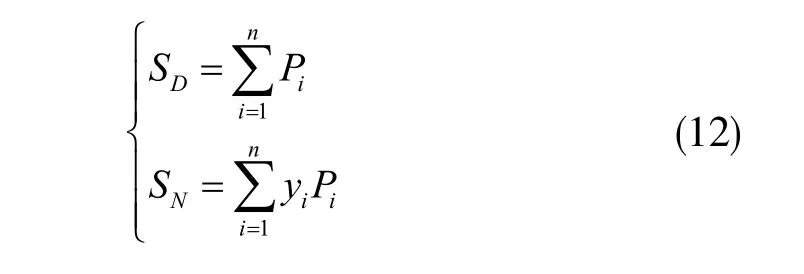
而输出层神经元的取值是将求和层的输出进行相除，即：

4.2 算法设计

综上所述，可以得到如下的小样本血糖浓度预测算法：

算法名称：小样本血糖浓度预测算法

输入：血糖原始序列yt（t=1,2,...,n）

输出：血糖序列的m 个预测值yt（t=n+1,n+2,...,m）

步骤1:利用式(1)耀式(5)对yt进行计算分析，若存在异常样本，跳转步骤2，否则，跳转步骤3；

步骤2：以步骤1 检测发现的异常样本点为中心，选取其左右相邻的4 个样本点，代入式(7)求得Lagrange 插值多项式函数，并将新的函数插值替换异常样本点；

步骤3：以[1,n]为插值区间，利用式(8)耀(10)求出对应的三次样条插值函数，并在各个子区间[t,t+1]（t=1,2,...,n-1）中，根据实际需要以细分的时间间距完成样本插值扩充处理，完成异常样本剔除及扩充处理的血糖序列记为

步骤4：将分拆为训练样本和测试样本，对广义回归神经网络进行训练，打印输出网络参数，算法结束。

5 实验及结果分析

为验证本算法的有效性及先进性，选取美国国立卫生研究院发布的DirecNet（Diabetes Research in Children Network)糖尿病临床数据集进行实验。该数据集有100 多名糖尿病儿童患者的连续血糖数值，采样时间间隔为5 min，由专业的连续血糖监测系统采集所得。

实验在PC 机上进行，硬件配置为：Intel 酷睿i5 4570 四核CPU、Kingmax DDR3 16GB RAM、Western Digital 500 G Hard Disk；操作系统与开发环境为：Microsoft Windows10、MATLAB R2013。

在实验过程中，着重对比现有算法与本算法在辨识精度和计算开销等技术指标上的差异，并对相关实验结果加以详细分析与讨论。

5.1 实验过程与方法

随机选取10 名患者的某1 天（24 小时）的血糖序列进行浓度预测建模分析，实验的过程包括：

步骤a：分别以Δt=1h、2h、3h、4h 对原始实验样本抽样，得到三种不同时间间隔的小样本序列；

步骤b：用式(1)耀式(7)分别对步骤a 中三种小样本序列进行异常样本点剔除和替换；

步骤c：用式(8)耀式(10)分别对步骤b 中的各种小样本序列进行三次样条插值的样本扩充处理；

步骤d：在MATLAB R2013 中，分别对各名患者的原始序列、不同时间间隔的小样本序列进行基于广义回归神经网络的预测模型的训练和构建。

5.2 实验结果与分析

5.2.1 原始血糖序列的各项预处理结果

以5#患者为例，其原始血糖序列如图2 所示。该血糖序列的采样时间间隔Δt=5 min，共有288 个样本点。

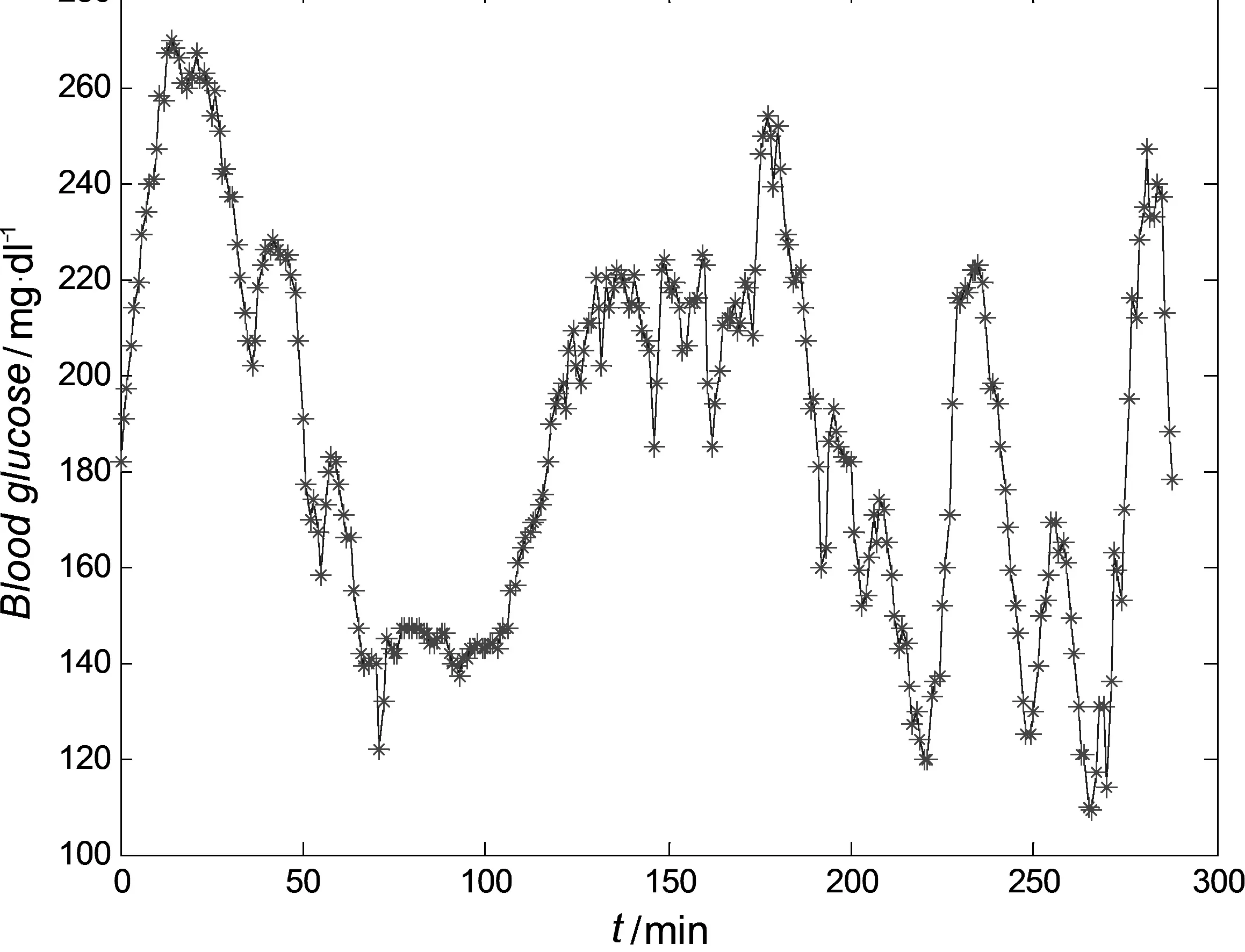
图2 5#患者原始血糖序列

图3 为以时间间隔Δt=1 h 对原始血糖序列做抽样处理所得的小样本序列，共有24 个样本点。

图3 时隔Δt=1h 抽样处理所得小样本序列

利用式(1)耀式(5)对图3 的小样本序列进行异常样本点处理，处理后的效果见图4。通过对比可见，在t=3 和t=22 处已完成异常样本的剔除和替换。

图4 异常样本点处理效果图

利用式(8)耀式(10)对图4 的小样本序列进行以时间间隔Δt=5min 的三次样条插值函数的扩充处理，处理结果如图5 所示。

图5 三次样条插值处理效果图

5.2.2 实验结果讨论

为验证各种不同时间间隔的小样本扩充序列的预测建模性能，此处将基于广义回归神经网络对原始血糖序列、Δt=0.5h、Δt=1h、Δt=2h 及Δt=3h 等4种小样本扩充序列进行预测建模分析。以连续4 个小时的相依血糖序列（共48 个样本点）对下一个血糖浓度进行预测，可设置广义回归神经网络的输入节点数n=48；将前232 个序列作为训练样本，后56个序列作为测试样本，模式层和求和层的神经元数目p=184。

为了全面考察各种不同时间间隔抽样所得的样本序列对预测精度的影响，引入平均绝对百分误差MAPE 进行有关的性能评价，MAPE 的具体定义为：

式中，yt为输入序列，为预测序列，n 为序列长度。

在糖尿病的实际临床治疗过程中，为了有效地确定注射胰岛素的最佳时间和剂量，医护人员往往需要对未来30 分钟范围内的血糖水平进行预测，以采样时间间隔Δt=5 min 为例，则需要对未来6 个样本点进行预测。继续以5#患者为例，将各种不同时间间隔抽样所得的扩充样本序列输入至广义回归神经网络中进行训练，并利用训练所得的网络模型进行未来6 个样本点的预测，得到图6 所示的预测效果图。分别对10 名患者的各种扩充样本进行相应的网络训练模型，各样本的MAPE 预测性能详细见表1 所示。

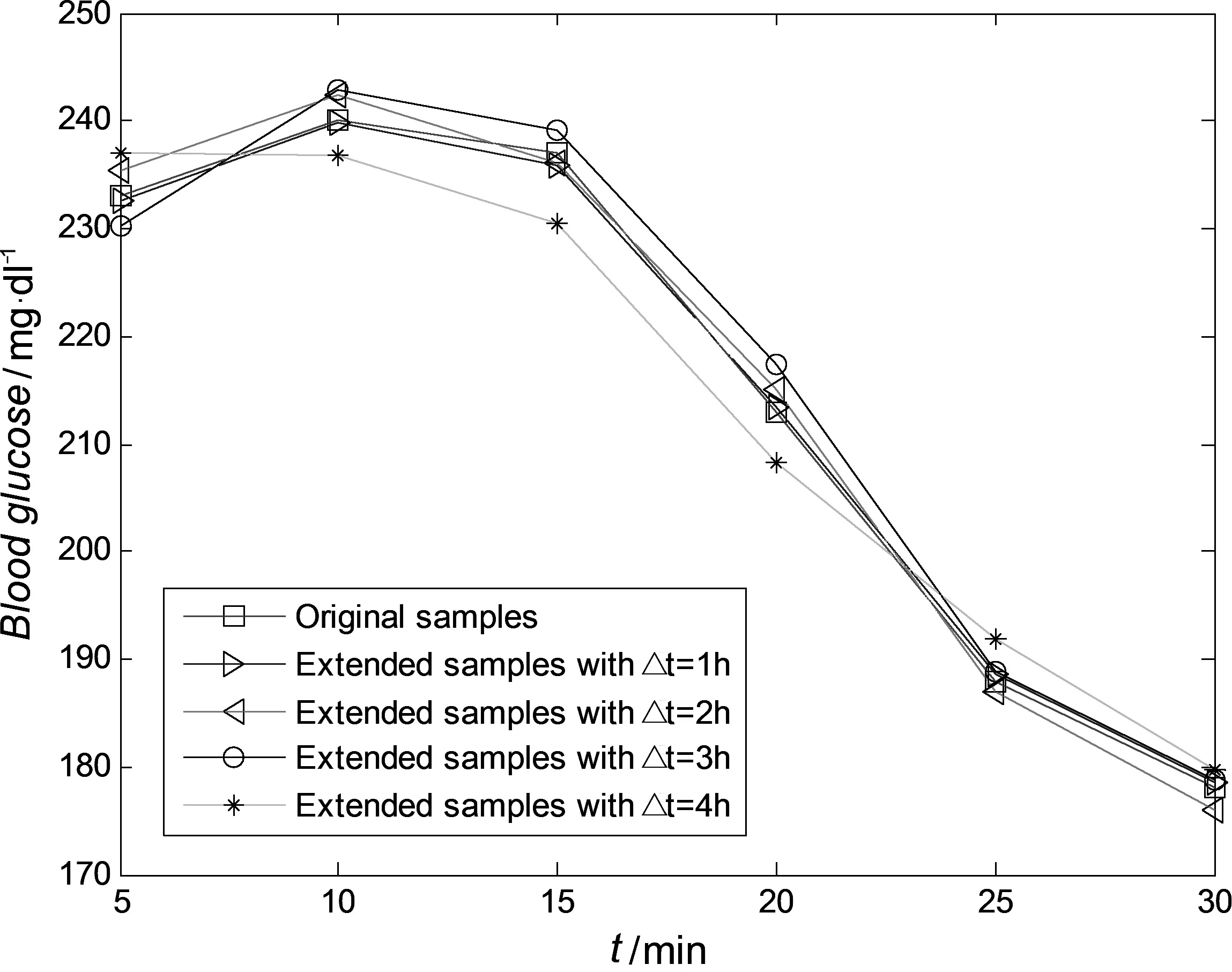
图6 5#患者各扩充样本序列6 步预测效果图

表1 各抽样小样本扩充序列MAPE 预测性能

从图与表中可知，对各患者而言，以原始血糖样本训练所得的模型预测精度最为精确，其MAPE 在98%耀99%之间；随着抽样时间间隔的增大，扩充样本训练模型的预测精度逐渐下降，在抽样时间间隔Δt=3 h 时，其MAPE 仍能维持在90%以上，此时仍属高精度预测。当抽样时间间隔Δt=4 h 时，MAPE已降至90%以下。在抽样时间间隔Δt=mh 时，其三次样条插值函数便需要插入60÷5×m-2 个样本点，不难发现，抽样时间间隔越大，插值样本数量就越多，相应地，插值误差也就越大。事实上，过多使用扩充样本进行网络训练，所得模型的预测性能确实在逐渐变差。

从上述分析可知，在保证高精度预测的前提要求下，通过三次样条插值函数的扩充处理，训练模型所需的样本抽样采集时间可以从5 分钟延长至3 小时。据此便可证明本改进算法是正确和有效的。

6 结 束 语

针对小样本血糖浓度预测的医疗实际需求，提出了一种改进的预测算法。改进算法通过对异常样本进行剔除和替换以及三次样条插值函数的样本扩充等处理，实现了在一定采样时间间隔的条件下，以较少的训练样本获得较为精确的预测模型。下一步的主要工作是研究性能更为优异的插值函数，以便实现延长抽样时间间隔的同时，进一步提升预测模型的精度。