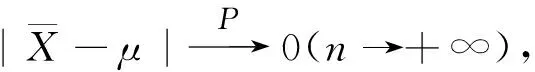样本的k阶中心绝对矩的依概率收敛性证明*
2021-03-04邢家省杨义川
邢家省,杨义川,吴 桑
(1.北京航空航天大学数学科学学院,北京 100191;2.北京航空航天大学“数学、信息与行为”教育部重点实验室,北京 100191)
在总体参数的矩估计的理论方法中,首先要考虑样本矩与对应的总体矩之间的关系.由辛钦大数定律[1-11]可知,简单随机样本的k阶原点矩依概率收敛到总体的k阶原点矩,样本的k阶原点绝对矩依概率收敛到总体的k阶原点绝对矩;由随机变量序列依概率收敛的性质[1-15]可知,样本的k阶中心矩依概率收敛到总体的k阶中心矩.由此得到用样本矩替换总体矩的理论根据,进而可以得到未知参数的估计方法,使得从局部参数就能推测总体参数,该方法称为矩估计法.关于样本的k阶中心绝对矩依概率收敛的问题,在文献[1-15]中都没有提及,而这是一个急需解决的问题.因此,笔者拟给出样本的k阶中心绝对矩依概率收敛的问题的解决办法,以期丰富完善样本矩依概率收敛理论.
1 总体矩和样本矩
设总体X的m阶矩存在,EXm和E(|X|m)存在,X1,X2,…,Xn为来自总体X的样本.记总体矩[1-11]:
μ=EX,
μk=E(Xk)k=1,2,…,m,
νk=E(X-EX)kk=1,2,…,m,
βk=E(|X|k)k=1,2,…,m,
δk=E(|X-EX|k)k=1,2,…,m.
记样本矩[1-11]:
2 随机变量序列依概率收敛的基本性质



利用依概率收敛的定义,可以给出引理1的证明.引理1在证明随机变量序列依概率收敛方面发挥重大作用.
引理2[1-15]设随机变量序列{ξn},{ηn}分别依概率收敛于随机变量ξ和η,则有:
引理3[1-12](辛钦大数定律)设{Xn}为独立同分布的随机变量序列,若Xi的数学期望存在,则{Xn}服从大数定律,即对于∀ε>0,都有

3 样本矩依概率收敛的性质
引理4[1-12]样本均值依概率收敛于总体期望,即
引理5[1-12]样本的k阶原点矩依概率收敛于总体的k阶原点矩,即
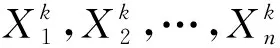
证毕.
由图3可知,当采用光滑轮胎进行试验时,摩擦系数的大小仅取决于轮胎与试件表面的接触面积,AC—13属于悬浮密实结构类型,表面构造深度较小、与轮胎的接触面积大,从而有较高的摩擦系数。对于花纹轮胎而言,都是OGFC—13的摩擦系数最大,主要是因为轮胎花纹能够嵌入到路面宏观纹理中,增强轮胎与路面的嵌挤力,表现为较好的抗滑性能。
引理6[1-12]样本的k阶原点绝对矩依概率收敛于总体的k阶原点绝对矩,即
证明由X1,X2,…,Xn独立同分布可知|X1|k,|X2|k,…,|Xn|k独立同分布,且E(|Xi|k)=βk存在.根据引理3可得
证毕.
引理7[1-12]样本的k阶中心矩依概率收敛于总体的k阶中心距,即
证明利用二项式展开和依概率收敛的运算性质可得
证毕.
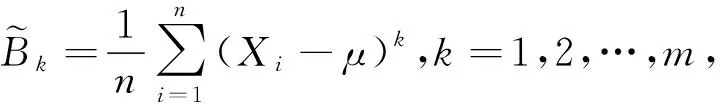
根据引理3可得

4 样本中心绝对矩依概率收敛的性质
引理8[16-19]设p>1,a,b≥0,则
(a+b)p≤2p-1(ap+bp).
证明由凸函数f(x)=xp,x∈[0,+∞)的性质可知
于是(a+b)p≤2p-1(ap+bp).证毕.
引理9[16-19]设p≥2,则对于实数a,b,有
||a|p-|b|p|≤|a-b|·p·2p-2(|a|p-1+|b|p-1).
证明不妨设|b|>|a|.由拉格朗日中值定理可知,存在满足|a|<ξ<|b|的ξ,使得|b|p-|a|p=pξp-1(|b|-|a|),于是
||b|p-|a|p|=pξp-1(|b|-|a|)≤|a-b|·p·(|a|+|b|)p-1≤
|a-b|·p·2p-2(|a|p-1+|b|p-1).
证毕.
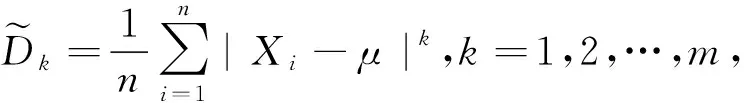
证明由X1,X2,…,Xn独立同分布和μ=EX为常数可知,X1-μ,X2-μ,…,Xn-μ独立,从而|X1-μ|k,|X2-μ|k,…,|Xn-μ|k独立同分布,且E|Xi-μ|k=δk存在.
根据引理3可得
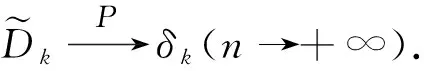
定理3样本的k阶中心绝对矩依概率收敛于总体的k阶中心绝对距,即
证明当k=1时,注意到
当k≥2时,由引理8和引理9,考虑如下估计不等式: