一种在线迭代聚类的多传感器一致性数据融合方法

周珍娟, 刁联旺

(1.江苏开放大学 信息与机电工程学院,南京 211135；2.中国电子科技集团第二十八研究所 信息系统工程重点实验室，南京 210007)

0 引言

多传感器数据融合是将来自各个传感器的测量数据进行综合处理,以获得更加精准、稳定和可靠的融合数据，从而尽可能地减少了多传感器测量数据经过融合处理可能产生的融合算法误差。为此在实施进行融合处理之前，需要对各传感器测得数据的真实性和可信性进行判定，即通过建立不同传感器测量数据间的一致性判定函数表达式，从而判明这些测量数据中的一致性并将允许它们参与融合处理过程。文献[1]对多传感器一致性数据融合算法的发展现状及存在的主要不足进行深入探讨。文献[2]借鉴信息质量的概念，基于传感器测量精度分级对一致性数据融合算法进行了一定的改进。文献[3]首先运用模糊集理论构造了测量数据间的相关性隶属度函数，用以度量各传感器测量数据间的相互支持程度并据此对其这些测量数据进行排序，然后将其中支持度较低的测量数据判定为异常数据予以剔除，最后彩递推最小二乘算法对保留下来的各个传感器测量数据进行融合以获得更精确的结果。文献[4]基于截尾正态分布的统计性质定义了多传感器测量数据间的不一致性，提出了一种基于统计加权算法平均的多传感器数据融合算法。文献[5]基于岭回归分析提出了一种度量多传感器测量数据相对可靠性的新算法，然后运用改进的最小二乘无偏估计对可靠性较高的测量数据进行融合的统计方法。文献[6]用传感器的测量精度建立了一种新的模糊支撑函数，并用该函数表示传感器测量数据的可靠性并用其确定测量数据的权重，最后采用线性加权方法融合多传感器的测量数据。文献[7]利用多元正态分布的统计特性以及其均值的假设检验，提出了一种度量多传感器的测量数据之间距离的新方法，该方法具有明确的统计意义，十分便于判定测量数据的一致性。虽然国内外学者们对多传感器一致性数据融合方法进行了大量理论和结合实际的应用研究，但总体上看，现有方法在判定多传感器测量数据间的一致性时，往往都是把高精度的传感器测量数据与精度 较低的传感器测量数据通过建立的各种距离函数求取一致性矩阵，然后根据该矩阵判定各种传感器测量数据的支持度，以确定哪些数据参与融合处理。这样的处理方法客观地讲它从方法的原理上就减少了哪些测量精度相对较差的传感器测量数据参与数据融合处理的可能性，自然丧失了多传感器数据融合带来的优势。本文针对这一问题，运用在线迭代聚类的思想，这样不仅可以发现不同传感器测量数据之间的一致性，而且还可以找出“率先”局部融合而形成的“复合传感器”数据间新的一致性，从而更好地揭示了多传感器测量数据间存在的深层次一致性，更充分地利用了多传感器测量数据，这对多传感器融合系统的实际工程应用具有较高的参考价值。

1 现有一致性数据融合方法的不足

本节简单介绍对现有多传感器一致性融合方法的基本步骤，重点分析了其存在的不足之处。

1.1 测量数据的统计分布

(1)

式中，i=1,2,…，n；xi是第i个传感器的测量值，μ为待测量的某一物理特征(如温度、长度、厚度等)的真值，而σi是第i个传感器测量误差的标准差。

多传感器一致性数据融合研究的重点问题是，当采集到各传感器的测量结果之后，如何判定这些传感器的测量数据间是否存在异常数据，即测量数据间是否具有一致性，从而选择具有一致性的传感器的测量数据参与融合处理。

1.2 一致性融合方法的基本步骤

现有多传感器一致性融合方法的基本流程如图1所示[8-9]。

图1 多传感器一致性融合的基本框架

1.3 现有多传感器一致性数据融合方法的不足

现有的多传感器一致性数据融合方法的基本步骤是，首先根据距离矩阵求取一致性关系(支持)矩阵R=(rij)n×n，然后根据该矩阵求取各个传感器的测量数据被其他传感器测量数据支持的总支持度，从而确立最大传感器连接组，最后可以采用贝叶斯统计方法、极大似然估计方法以及其它线性/非线性加权方法对最大连接组中的传感器测量数据进行融合[1-5]。通过分析可以发现此处理方法主要存在以下不足：

1)在确立最大传感器组时，主要依据的是各个传感器组包含的传感器数量，而对传感器的精度未加考虑。显然这种不重数量、不重质量的方式是不正确的，例如在3个传感器测量同一对象时，尽管其中两个较差的传感器测量数据具有很高的一致性，但它们却与三者中最好的传感器测量数据一致性很低，无疑这两个传感器(数量多！)测量数据的融合结果未必比最好但不一致传感器测量数据更接近于被测真值。

2)在判定多传感器的测量数据一致性时，通常的做法是基于一致性矩阵进行一次解决问题的决断，而对部分传感器测量数据局部融合结果如何未加以分析，仿真试验结果表明，这是现有多传感器一致性数据融合方法存在的最大缺陷！比如，在各传感器测量数据服从正态分布且相互独立的假定下，可以证明用贝叶斯估计方法得到的融合结果也是服从正态分布的，且该分布的标准差要比参与融合处理的各个传感器中任何一个传感器的标准差都要小，实际应用中也发现，若对其中具有一致性的测量数据进行局部的融合，这些融合结果中极有可能与其余传感器的测量数据通过一致性判定，因而会扩大参与融合处理的传感器数量，从而能够提升融合结果的精度，然而这种一致性则由于现有数据一致性一次性判定处理的思维方式所忽略！文献[7]针对这一问题提出了一定的改进，但仍然未消除由于数据一致性判断带来的信息丢失问题。

2 基于在线迭代聚类的一致性数据融合算法

本文利用在线迭代聚类的方法以判断不同精度传感器测量数据间是否具有一致性，该方法通过对多传感器测量数据的在线迭代判定处理，可以有效地解决判定多传感器测量数据一致性时发生信息丢失问题。下面首先定义一种度量传感器测量数据间距离的新方法，该距离中有效地体现了传感器测量精度的重要作用。

2.1 基于统计假设检验的概率距离

(2)

可见，只有在

(3)

成立时，才拒绝两个正态分布的均值是不相等的原假设。式中，k1-α/2为标准正态随机变量的双侧置信水平为α上门限值，通常可取0.05和0.01等。

在进行多传感器数据融合之前，为了剔除测量数据中的野值，通常需要对获得的测量数据进行一致性判断以选择合适的测量数据参与融合处理，这样处理可以有效地避免异常数据带来的融合误差，因此已经成为工程实践中的标准做法。在前述假定之下，本文提出如下距离函数dij，以度量传感器i个和传感器j的测量数据间的相互支持程度：

(4)

式中，xi,xj是传感器i和传感器j的测量值；σi，σj为两个传感器对应的标准差。Z表示随机变量，它服从标准正态分布。

式(4)给出的dij表达式，是可以作为度量两个传感器测量数据间的距离的，因为可以证明它满足距离函数的性质[8]，称之为概率距离。

2.2 一致性关系矩阵

根据式(4)可以定义判定任意两个传感器测量数据间的一致性关系rij，判断方法如下：

(5)

式中，α为判断门限值，通常可以取为0.01，0.05和0.1。其中，rij=1表示传感器i和传感器j的测量数据具有一致性，可以参与融合处理；否则rij=0表示传感器i和传感器j的测量数据是不一致的，因此，两者的测量数据是不应同时参与融合处理的。

2.3 在线迭代聚类融合算法的基本步骤

本文提出一种在线迭代聚类的多传感器一致性数据融合方法，其主要步骤分为：

假定有n个传感器参与对某一被测对象的测量过程，这n个传感器的某一次测量获得的数据分别记为x1,x2,…,xn，各个传感器测量精度(即传感器测量误差的标准差)分别记为σi，i=1,2,…,n；

步骤1：将每一个传感器的测量数据视为一个类对象，则此时每类中只有一个对象，按式(4)计算传感器i和传感器j的测量数据间的距离dij，此时类与类间的距离实际上就是它们各自所包含的类对象间的距离，计算结果可以表示为一致性判断矩阵，记为D=(dij)n×n；i≠j,i,j=1,2,…,n；

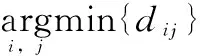
(6)

(7)

将包含传感器i和传感器j的两个类合并成一新的类，不妨称之为“复合传感器”(i,j)，可以把x(i,j)视为该“复合传感器”的一次测量结果，该传感器相应的测量精度为σx(i,j)。并返回步骤1)进行迭代处理；

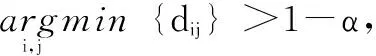
步骤3：此时将会出现两种情况，

1)情况1：所有类都归并到了一个类中，此时所获得“复合传感器”将是唯一的“复合传感器”，因此它的测量结果即为该情形下多传感器测量数据一致性融合的最终结果；

2)情形2：所有类归并为m个类(n≥m≥2)，此时由于各类中的数据间不再能通过一致性判断检验了，因此最终对获得的多传感器测量数据的一致性数据融合结果将会在这m个类中产生，从中选择融合精度最高者作为该次多传感器测量数据的一致性融合结果。

从上述的算法描述中可以看出，本文提出的在线迭代聚类的一致性数据融合算法的最大优点是不再把不同测量精度的传感器测量数据放在一起计算一致性矩阵，并据此作出一次性判断或分层融合判断[7]，而是根据聚类分析的结果，对能通过一致性检验传感器测量数据，依据数据间的距离大小先进行局部的一致性融合，然后再把局部融合结果作为一个虚拟的传感器(称之为“复合传感器”)测量数据，将其与余下传感器的测量数据再进行一致性判断计算，若还有通过一致性检验者再进行融合处理，这一通过返复迭代，直至不再具有通过一致性检验的数据为止。显然本文提出的算法对多传感器测量数据间的一致性判定更符合一致性本质内涵，即不仅可以判断出原始的n个传感器测量数据间的显在一致性，而且还可以发现经过某些局部一致性数据融合后与其它传感器的测量数据间产生的新一致性，这种潜在一致性的发现可以更充分多传感器测量数据的效用。另外，由于每次迭代聚类合并产生的新的类对象要与其他类进行一致性判定，还需要重新计算合并后的类间距离，显然这样的操作会增加一定的计算量。但好在实际应用系统中传感器数量通常并不大(一般不超过10个)，因此增加的计算量完全是可以接受的。

3 计算举例

本节给出一个算例，用以说明本文提出的在线聚类一致性数据融合算法的基本步骤及其优越性。

假定某一多传感器测量系统由10个传感器构成，用以测量某一对象的物理特性参数(如距离、温度等)，该对象的真值为1.0，表1给出了此10个传感器的标准差，用Matlab产生随机正态分布的随机数，获得一次仿真数据结果如表1所示。

表1 10个传感器的精度指标与测量数据

采用式(4)定义的概率距离可以得到矩阵D为:

可见，传感器5和传感器8之间的距离最小(0.050 7)且小于门限值(此例中取0.95)，对这两个传感器的测量数据用式(6)和(7)进行融合：

x(5,8)=0.9972，σx(5,8)=0.0071

然后将上式结果看作一个传感器(虚拟的复合传感器记为S(5,8))的测量数据，此时变成了一个9传感器的传感器组，限于篇幅，这里不再给出详细地计算的过程以及得到的概率距离矩阵，仅列出该距离矩阵中相应的最小概率距离和融合计算结果。

1)可以计算出此时的概率距离矩阵(此时有9个传感器)中，传感器4与传感器6间的距离最小(0.062)且小于门限值0.95，因此传感器4和传感器6的测量数据可以进行局部融合：

x(4,6)=1.0108，σx(4,6)=0.0071

将上式计算结果看作是虚拟传感器S(4,6)的一次测量数据；

2)此时还有8个传感器，计算出距离矩阵，且可以计算出传感器2和传感器3间的距离最小(0.145 9)且小于门限值0.95，因此传感器2和传感器3的测量数据可以融合为：

x(2,3)=0.9991，σx(2,3)=0.0035

将上式计算结果看作是虚拟传感器S(2,3)的一次测量数据；

3)此时还有7个传感器，通过计算距离矩阵，可以看出传感器S(2,3)和传感器S(4,6)间的距离最小(0.265 7)且小于0.95，因此传感器S(2,3)和传感器S(4,5)的数据可以融合：

x(2，3，4，6)=1.0014，σx(2，3，4，6)=0.0031

并将其看作虚拟传感器S(2,3,4,6)的测量值；

4)此时还有6个传感器，通过计算距离矩阵可以看出传感器S(2,3,4,6)和传感器7间的距离最小(0.198 1)且小于门限值0.95，因此传感器S(2,3,4,6)和传感器7的测量数据可以融合为：

x(2,3,4,6,7)=1.0015，σx(2,3,4,6,7)=0.003

并将其看作为传感器S(2,3,4,6,7)的一次测量值；

5)此时还剩下5个传感器，通过计算距离矩阵可以发现传感器S(2,3,4,6,7)与传感器S(5,8)的距离最小(0.6892)且小于门限值0.95，因此传感器S(2,3,4,6,7)与传感器S(5,8)的测量数据可以融合为：

x(2,3,4,5,6,7,8)=1.0008，σx(2,3,4,5,6,7,8)=0.0028

并将其看作虚拟传感器S(2,3,4,5,6,7,8)的一次测量数据；

6)此时还剩下4个传感器，通过计算距离矩阵，可以发现传感器1与复合传感器S(2,3,4,5,6,7,8)间的距离最小(0.9186)且小于门限值0.95，因此传感器1与复合传感器S(2,3,4,5,6,7,8)的测量数据可以融合为：

x(1,2,3,4,5,6,7,8)=1.0031，σx(1,2,3,4,5,6,7,8)=0.0024

并将其看作是虚拟传感器S(1,2,3,4,5,6,7,8)的一次测量值；

7)此时还有3个传感器，通过计算距离矩阵可以发现传感器9和传感器10间的距离最小(0.9494)且小于门限值0.95，因此两者的测量数据可以融合为：

x(9,10)=1.0038，σx(9,10)=0.0141

并将其看作是虚拟传感器S(9,10)的一次测量值；

8)此时还有两个传感器，通过计算可以得到两者间的距离为0.163 4小于门限值0.95，因此两者的数据可以融合为：

x(1,2,3,4,5,6,7,8,9,10)=1.0027，σx(1,2,3,4,5,6,7,8,9,10)=0.0024

对于同样的数据，若采用最大传感器支持组的算法，可以得到最大一致传感器组为:

{S1,S2,S3,S4,S5,S6,S7,S8}

因此可以计算出最终的融合结果为：

x(1,2,3,4,5,6,7,8)=1.0035，σx(1,2,3,4,5,6,7,8)=0.0028

可见其融合结果无论是均值还是标准差都较本文提出的算法获得的结果要差一些。

用Matlab软件对表1所示的多传感器测量系统进行仿真试验，仿真中一致性判定的门限分别取为0.80, 0.85, 0.90和0.95，对于不同的门限值各进行了100次仿真试验，并将本文所提算法与文献[1,4,9]的3种一致性融合算法进行比较，结果列入表2。

表2 三种算法的仿真结果比较

从表2可见，对不同阈值仿真计算结果表明：本文提出的算法可以获得更好的融合结果。

4 结束语

本文讨论了多传感器测量系统数据融合问题，针对现有多传感器一致性数据融合方法存在的不足，运用迭代的聚类算法，将具有一致性传感器组融合结果视为虚拟的复合传感器测量数据，进行迭代聚类运算，以发现更多的潜在数据一致性，既可避免异常测量数据参与融合处理，又可以提高了融合的准确度，而且也提高了融合结果的精度。本文提出的方法可以应用于多雷达测距系统，也可以应用于工业领域中的多传感器测量管壁厚度等系统。需要指出的是本文提出的方法需要付出了一定的计算代价，但实际多传感器测量系统中传感器数量并不多，增加的计算量不会带来很大的困扰，是可以接受的。