一种六足仿生巡检机器人的设计与实现

谢 玮,陈家明,陈 军,孙 华

(1.哈尔滨工业大学(威海) 信息科学与工程学院，山东 威海 264209;2. 哈尔滨工业大学(威海) 船舶与海洋工程学院，山东 威海 264209;3. 上海化学工业区公共管廊有限公司，上海 201424)

0 引言

随着机器人技术的发展，其应用越来越广泛，特别是在许多人类难以到达或者危险性较高的场合[1]，如救灾、巡检、深海探测和核电厂维护等，机器代人势在必行。同时，随着人工智能技术的发展，机器人系统已经逐步具有较高的环境适应能力和自主决策能力，因此在特定场合替代人工巡检具有很多优势。与轮式和履带式巡检机器人相比较，仿生足式机器人对复杂地形的适应能力更强，工作效率更高，具有灵活度好、可靠性高、适应性强的独特优势[2]。

六足仿生机器人由于肢体冗余度较高，其稳定性和负载能力比一般机器人更高，具有丰富的步态和一定的故障容错能力，一直以来都是国内外机器人研究的热点[3]。如何进行合理有效的步态规划、实现各肢体的协调运动，以及六足机器人模型的简化工作，仍是目前研究的重点和难点。国外许多研究机构开发出了多种先进的六足机器人，如美国加州理工大学设计的采用超轻晶圆电池提供动力的小型六足机器人Spider-bot[4]，日本大阪大学研制的手脚两用的机器人asterisk[5]和德国卡尔斯鲁厄大学研发的六足机器人Lauron IV[6]等。国内典型的有上海交通大学研制的用于灾难救援和环境探测的“六爪章鱼”机器人[7]，北京航空航天大学开发的圆周对称分布结构的NOROS机器人[8]，哈尔滨工业大学设计的以竹节虫为参考模型的六足机器人HIT-Spider和HITCR-II[9-10]等。由此可见，国内外均已在六足仿生机器人的研制上取得了较大突破，在巡检方面的应用将会向实用性、轻量化和智能化的方向发展。

对于机器人爱好者或者初级研究者来说，要做一个实用化的六足仿生机器人还是会面临很多困难。本文以一种六足仿生巡检机器人的系统设计为例，从结构设计、步态规划、系统仿真和实物构建等各方面，探索一般意义上的六足仿生机器人系统的设计和实现方法[11-12]。

1 系统结构设计

1.1 六足仿生机器人结构设计

根据仿生学原理，六足机器人的六条步行腿在其身体的两侧呈对称分布，每条腿都具有3个关节，分别称为髋关节、膝关节和踝关节，如图1所示。因此，机器人的每条腿都有3个旋转自由度。

图1 六足机器人步行腿分布及单腿关节分布

从仿生的角度来看，动物在运动过程中腿的运动状态可分为支撑和摆动两个过程。类比到足式机器人身上，则机器人的腿部运动也可分为支撑相和摆动相。为了使机器人快速而稳定地运动，就需要协调各步行腿之间的运动。从机器人左前腿开始编号，分别将左前腿、左中腿、左后腿、右后腿、右中腿、右前腿编为1号到6号，如图1所示。结构设计的要点是要模拟动物的一种稳定步态，即在行走过程中，始终有三条腿支撑在地面上，构成稳定的三角形结构支撑身体运动。对于图1的六足机器人来说，会选择1号、3号和5号即左前腿、左后腿和右中腿这三条腿同步运动，同时选择2号、4号和6号即左中腿、右后腿和右前腿这三条腿同步运动。对于单个腿而言，为保证摆动相和支撑相时间相同，增加行进中位和静止这两个中间过程，则单个步行腿的运动过程按时间顺序分为抬腿、迈腿、放腿、行进中位、收腿和静止6个状态。机器人依靠腿部的摆动和肢体的协调来维持身体平衡和实现行走。

从运动学的角度看，图1所设计的仿生机器人的腿更像是一个机械臂。因此可用一个三轴串联关节型机器人的建模和分析方法来设计。可用标准D-H参数法建立机器人的单腿数学模型，这样就可以把抬腿、迈腿、放腿、行进中位、收腿和静止6个状态转化为运动学模型的求解和规划，实现更加精准的步态控制。

1.2 单腿的运动学模型建立

将六足机器人的单腿当作一个三关节串联机械臂结构进行分析和建模。首先为一个三关节的机械臂规划路径，即为机器人的一条腿规划轨迹，根据足端的运动轨迹求解逆运动学问题得到各关节的关节角变化，进而根据相位关系得到其他腿的轨迹和关节角，并将它们组合成一个整体，即可得到六足机器人的步态。

对单腿进行建模，首先要建立坐标系，将坐标系的原点建立在机器人髋关节的中心处，如图2所示。为了方便研究腿的抬起和放下，令Z轴朝下，X轴朝向机器人前方，因此Y轴就指向图示右侧，即机器人的外侧。使用标准D-H参数法对机器人的腿机构建立数学模型，机械臂的3个关节分别实现机器人髋关节、膝关节和踝关节的转动，而3个连杆则按照实际长度设计，其D-H参数如表1所示。其中，j表示关节编号，theta为关节角，d为连杆偏移，a为连杆长度，alpha为连杆扭转角；offset为关节偏置量，用来调整各关节的初始位置。表中负值表示与标准D-H参数法定义的坐标系正方向相反，所有参数单位为标准国际单位。

图2 机器人腿部模型及其坐标系

表1 机器人腿部D-H参数表

根据D-H参数，就可求出机器人每个腿的关节角度与末端位姿之间的对应关系。而且为仿真和步态规划提供理论基础。

2 步态规划方法

2.1 步态规划基本原理

对于面向巡检类的机器人来说，步态规划是路径规划的充分条件。描述动物的步态除了支撑相和摆动相之外，还有步态周期T、占空系数β、步幅和支撑多边形等，其中T和β尤为重要。步态规划的核心要义就是在行走过程中，始终有三条腿支撑在地面上，构成稳定的三角形结构支撑身体运动。

步态周期T主要是指完成一个步态所需要的时间，也就是机器人所有腿依次按顺序完成抬腿、迈腿、放腿、行进中位、收腿和静止动作所花费的时间，在此过程中机器人机体也完成相应运动。

占空系数β是指机器人的某个步行腿在地面上支撑身体所用的时间占整个运动周期所需时间的比例，具体定义如式(1)所示：

(1)

式中，Tst为单腿在一个步态周期内处于支撑相的时间，Tsw为单腿在一个步态周期内处于摆动相的时间。

六足仿生机器人的步态随占空系数β的不同而变化。大多数研究者认为，当β=1/2时，六足机器人在整个运动过程中始终有三条腿在地面上支撑身体，且单个步行腿摆动相和支撑相的时间相同，运动的效率较高。

基于上述原理，六足机器人的纵向行走包括前进、后退、转弯等运动，六足机器人的横向行走是一种类似螃蟹步态的行走运动，因此可采用重心随动的三角步态规划方法来设计机器人的运动步态。

2.2 运动稳定性分析

将足式机器人各支撑腿与地面的接触点按顺序依次连接起来，以此构成的封闭凸多边形在水平面上的投影，称为多足机器人的支撑多边形。在运动过程中，若机器人质心的投影始终位于其支撑多边形内，则认为其在运动过程中始终具有运动的稳定性。在此引入稳定裕度的量化方法来衡量相对稳定性的大小。

忽略单腿摆动对质心位置变化的影响，即认为机器人在行走过程中，质心始终落在其几何中心上。质心投影到支撑多边形各边的距离为d1、d2和d3，则可按式(2)来定义机器人的稳定裕度：

S=min{d1,d2,d3}

(2)

稳定裕度描述了机器人在运动过程中相对稳定性的大小，稳定裕度越大，运动的静态稳定性越高，机器人不容易发生倾倒侧翻等故障。因此在一些复杂的环境中，需要根据稳定性分析，选择合适的步态，统筹兼顾运动的快速性和稳定性要求。

2.3 典型的步态分析

根据2.1的步态规划原理，我们把图1的多腿分布分成两组。把1、3、5号腿作为A组，将2、4、6号腿作为B组，同组的各步行腿在整个运动过程中始终保持同步动作。先令A组腿支撑在地面上，B组腿向前迈一步，与此同时A组腿向后摆动，推动机器人前进；然后 B组腿支撑在地面上，A组腿向前迈一步，与此同时B组腿向后摆动，推动机器人前进。在此过程中机器人的重心随运动过程发生变化，因此称之为重心随动的三角步态。

单个步行腿的运动过程，按照具体运动细分为抬腿，迈腿，放腿，收腿。同时，为保证摆动相和支撑相时间相同，增加行进中位和静止这两个中间过程，则单个步行腿的运动过程按时间顺序依次为：

1)抬腿：将腿竖直抬起离开地面，为腿的移动做准备；

2)迈腿：在水平方向移动腿，使腿运动到目标位置的正上方；

3)放腿：将处于目标位置的腿放下，起到支撑的作用；

4)行进中位：使腿部摆到目标位置和起始位置的中间位置，利用摩擦力移动身体。增加这一中间过程能使步态更加稳定协调；

5)收腿：使腿进一步摆动，回到开始运动时的动作，利用摩擦力使身体前进；

6)静止：腿保持不动。

两组腿之间的运动顺序如表2所示，按时间先后从左到右进行。两组腿分别按照表2的顺序动作，即可实现稳定而协调的三角步态。

表2 步行腿运动过程

3 系统仿真方法

使用Peter Corke编写的Robotics工具箱进行仿真测试。具体根据表1的D-H参数进行系统运动学建模，依据2.3给出的典型步态规划方法从以下两个方面进行仿真测试。

3.1 向前纵行的运动仿真和稳定性分析

按照2.3的方法规划机器人向前纵向行走时的单腿足端运动轨迹。首先根据三足步态和实际数学模型，定义足端各方向的运动极限，计算出足端运动轨迹的起点、中间点和终点的相对位置，解算出机器人每条腿部动作对应足端相对坐标。图3是在实现期望步态的过程中，单腿关节角的变化过程，图4为六条腿协调运行时的仿真运行位姿。

图3 关节角随时间变化的曲线

图4 机器人向前纵行仿真动画

图4中，设机器人的运动周期的起点为A组(0.08, 0.13, 0.1)，B组(0, 0.13, 0.1)。由于两侧的腿都沿直线运动，且各支撑点相对身体平面的距离都相等且保持不变，因此机器人的身体会沿直线平稳前进，继而实现了平稳的纵行步态。

由于三角形的重心始终位于三角形内，且很容易求得，所以只需比较机器人质心与支撑多边形的重心是否位于三条直线(三条边所在直线)的同一侧即可。经过验证，机器人质心位置始终满足要求，本实验中实现的六足机器人纵向直线行走步态满足静态稳定性的要求。运动过程中按照式(2)定义的稳定裕度数值如图5所示。

图5 稳定裕度随时间变化的曲线

3.2 向右横行的运动仿真及稳定性分析

基于三角步态实现的横向行走，相较于纵向行走只是改变了运动方向，只需对关节空间的运动轨迹进行调整即可实现。除此之外，两侧腿在y方向上的坐标变化不再相同，但仍是对称的，因为机器人需要平稳运动。仍然将六条腿分为A、B两组，以机器人身体右侧腿的运动为例，按照处理纵向行走步态的方法，定义足端各方向的运动极限和解算机器人右腿动作对应足端坐标。得到腿部各关节的角度变化，如图6所示。按照3.3中的方法进行仿真，运动周期的起点为A组(0, 0.17, 0.1)，B组(0, 0.13, 0.1)，运动过程中的某个截图如图7所示。仿真实现了平稳的横行步态。

图6 右腿关节角随时间变化的曲线

图7 机器人向右横行仿真动画

运动过程中按照式(2)定义的稳定裕度数值如图8所示。可以看出，整个运动过程中稳定裕度都较大，且稳定性要比向前纵行时要好。经过验证，机器人质心位置始终满足要求，本实验中实现的六足机器人横向直线行走步态满足静态稳定性的要求。

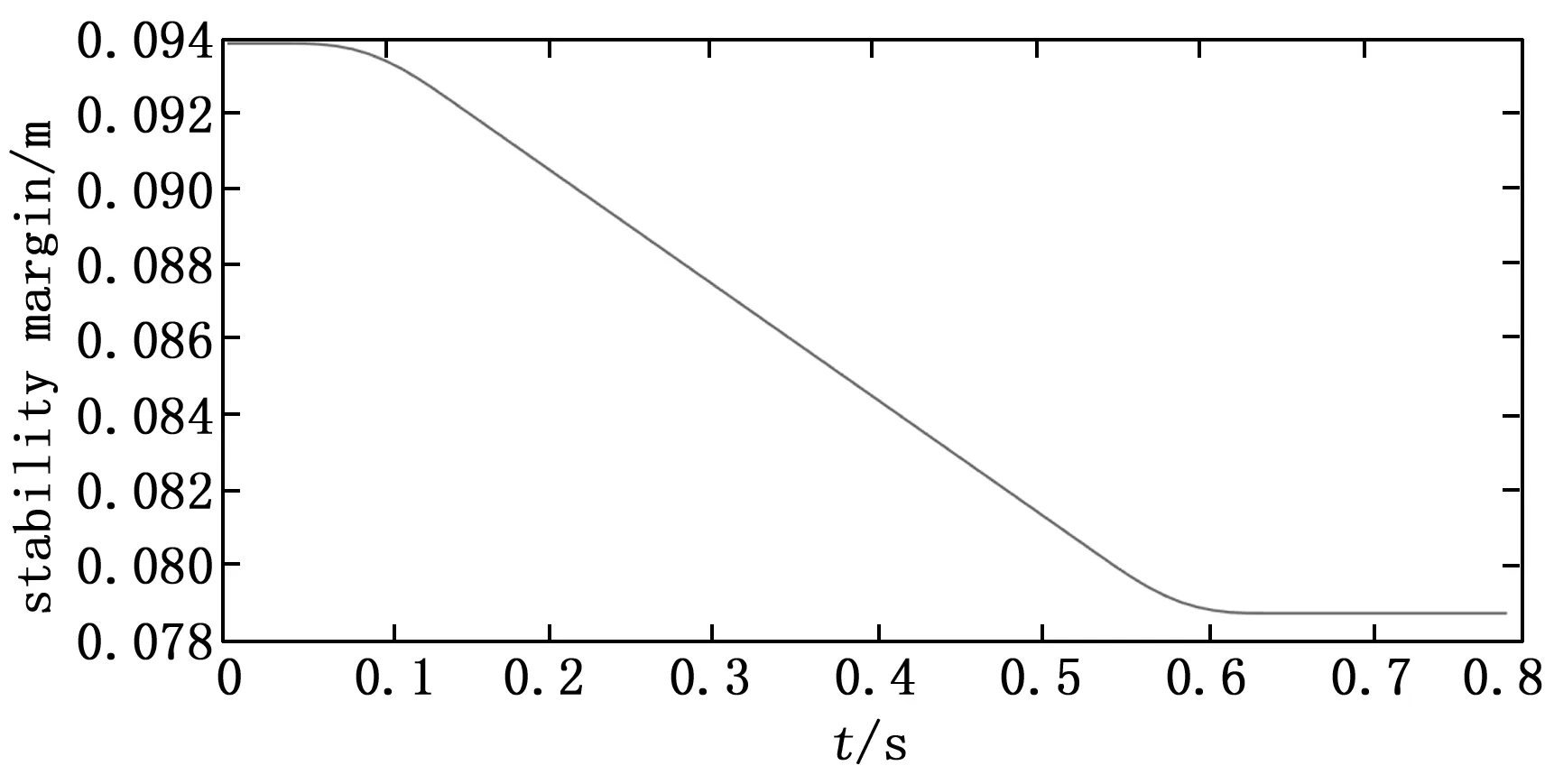
图8 稳定裕度随时间变化的曲线

通过3.1和3.2的仿真测试表明，2.3给出的步态规划方法可以实现机器人的纵向运动和横向运动，基本能满足系统的设计要求。

4 实物构建和验证

按照仿真验证的系统功能要求，我们采用了博创尚和公司的创意之星配件和控制器，选择CDS 5500系列舵机作为关节构件，搭建的六足机器人实物，测试得到六足机器人纵行和横行运动的数据。由于有避障的要求，六足机器人可能需要走复杂曲线，因此可以在仿真理论数据的基础上稍加改动即可。同时，为了提高机器人运动的稳定性，应在运动交替的时候加入一段共同的支撑时间。实验数据如表3所示，其中1、3、5为A组，2、4、6为B组，11、

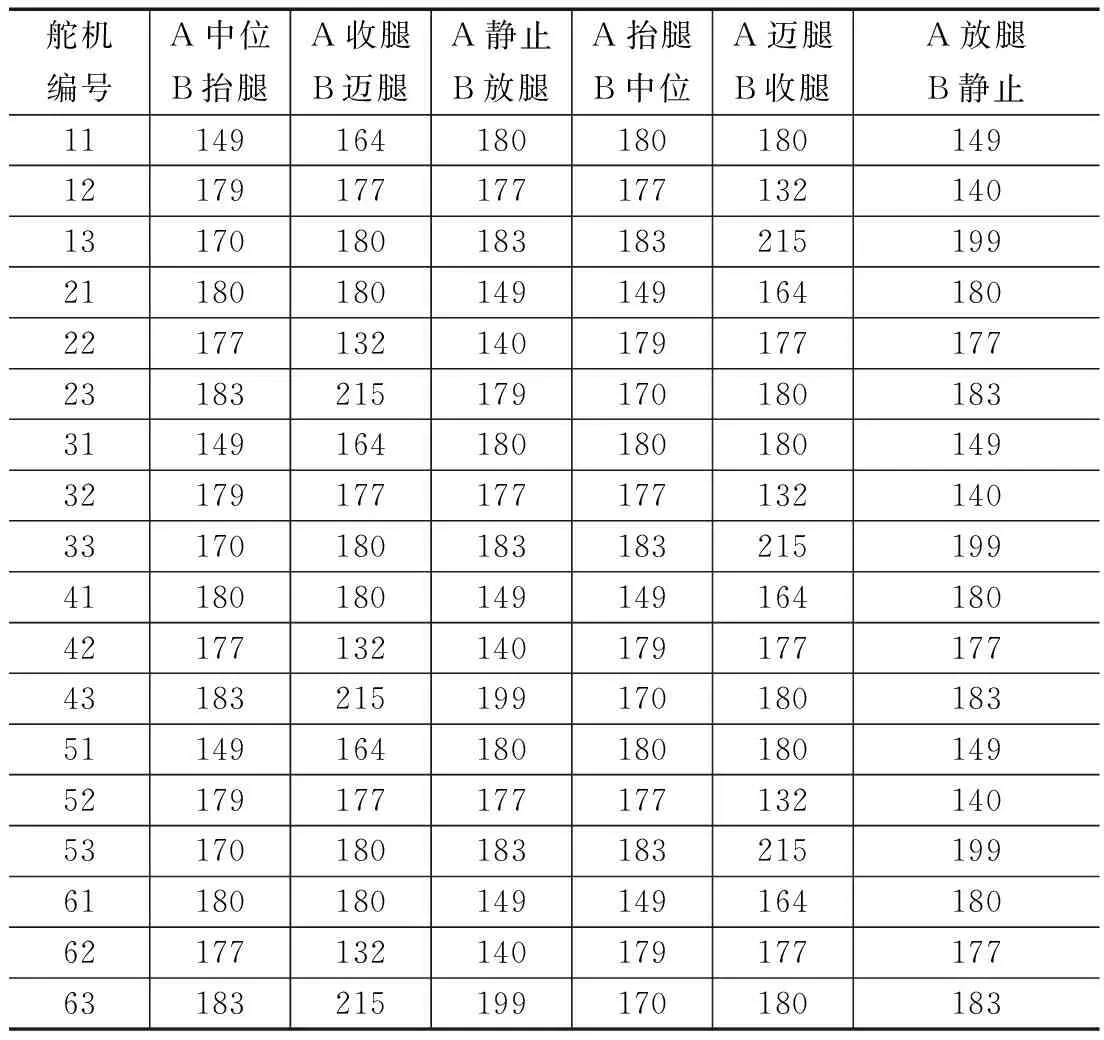
表3 纵向行走的实验数据 (°)

12和13分别代表左前腿髋关节、膝关节和踝关节的舵机输出角度，以此类推。表中的数据已按照实际情况增加了180°，且分别对应各动作的起点位置。

运动过程如图9所示。

图9 运动过程图

机器人向右横向行走的结果如表4所示。

表4 横向行走的实验数据 (°)

在实物上进行了测试，并且能满足设计要求，很好地实现了三足步态的纵行运动和横行运动，且避障性能良好，符合预期目标。

5 结束语

近年来，由于人类探测环境越来越复杂和恶劣，六足仿生机器人获得了更广阔的应用，其灵活度好、可靠性高、适应性强的特点具有很大的实际意义。本文以一种六足仿生巡检机器人的系统设计为例，从结构设计、步态规划、系统仿真和实物构建等各方面，给出了一般意义上的六足仿生机器人系统的设计和实现方法。最后搭建了六足仿生巡检机器人样机，证明了三足步态规划的合理性。这个机器人系统分析和设计流程完全可以推广到其它类型的机器人系统设计流程中去。

另外，在本文实现的三足步态的基础上，还可以实现其他步态，如四足步态、五足步态、转弯步态等。本文主要采用运动学建模的方法，未来要考虑如何采用动力学补偿方法精准的控制机器人的位姿和关节力矩。当然，可以在本文搭建的六足仿生巡检机器人样机的基础上，为机器人增加摄像头、无线遥控和巡检检测传感器，以适应更多的巡检应用场合，比如公共管廊检测等，这些都有待于未来进一步的研究。