基于Kinect的动态手势识别研究
2021-03-04邵天培留沧海
邵天培,蒋 刚,留沧海
(1.西南科技大学 制造科学与工程学院,四川 绵阳 621010;2.制造过程测试技术省部共建教育部重点实验室,四川 绵阳 621010;3.成都理工大学 核技术与自动化工程学院,成都 610059)
0 引言
随着人类社会和机器人领域的不断发展,人类与机器人在各个方面也在不断地融合,机器人逐渐融入到了人类的生产制造过程和生活中,人类与机器人的关系日益密切,这就迫切地需要人类与机器人进行交互,从而能够比较顺利地实现人机合作与人机共融[1]。在人机交互领域中基于视觉的手势识别因为具有简单、直观、表达能力突出且自然的优势逐渐成为研究热点[2-5]。Bertsch等人[6]在仿人机器人平台上构建了基于视觉的人机交互系统,该研究使用隐马尔可夫模型识别动态手势,但是这种方法准确率不高且易受光照影响。Thinh 等人[7]在机器人上安装手机,利用手势通过手机上的摄像头与机器人进行交互。随着Kinect的问世,进一步弥补了人机交互方式上硬件的不足[8]。王兵等人[9]基于Kinect采用指尖检测算法并针对运动轨迹中运动方向的变化,提取了动态手势的特征并识别各个手势。Y.Gu等人[10]利用 Kinect并基于骨骼特征,使用隐马尔可夫模型训练进行测试,但该方法平均识别率不高且数据训练复杂。本文针对动态手势识别准确率不高且易受光照影响等问题对动态手势识别进行了研究。
1 动态手势识别
动态手势识别通过关注分析视频序列中的连续手势轨迹信息来判断手势语义,而不关注手型[11]。本文将基于Kinect传感器进行动态手势识别,Kinect会首先采集视频序列中的用户手势,然后依次进行手势分割、手势质心计算、手势轨迹特征计算,最后进行手势轨迹特征识别。
1.1 手势分割
手势分割是指将人手准确地从简单或复杂背景环境中分割出来[12,13],这是极其重要的一步,因为手势分割的好坏会影响后续环节。手势分割部分的难点在于目标手势易受光照和环境的影响。常用的方法,比如单纯利用肤色进行手势分割[14],则会把类肤色物体包括进来,在室内不同光照下利用肤色进行分割,效果如图1所示:从图1(a)可知,肤色分割虽然完整分割出了手势,但也将人的面部和类肤色物体一起包括。从图1(b)可知,在室内较弱光照条件下,分割出的手势甚至不完整,所以光照条件的改变会令手势分割变得异常困难。

图1 不同光照下基于肤色的手势分割结果
而利用Kinect采集的深度图像信息则会在进行手势分割时有效减少光照条件带来的影响。这是因为Kinect采集的深度图像存储在一个二维数组里[15],数组中的每一个像素点表示该像素点到传感器的距离,由于做一组动态手势时人手通常离传感器最近,所以可从绘制出的深度图像直方图中找到较小的灰度级,设定不同的阈值就可以准确地从背景中分割出感兴趣区域,再将感兴趣区域转换成二值图像即可。经过上述操作,就可以完整地从背景中分割出目标手势。如图2(a)右侧所示为较强光照条件下的深度图像,图2(b)左侧为深度图像直方图,右侧为手势分割结果,其中,深度直方图中圆圈所在横坐标为选定阈值的大概范围,该范围根据不同距离选取不同的值。本文中阈值范围为35~44左右,下同。

图2 较强光照下基于深度信息的手势分割结果
较弱光照条件下,利用深度信息对目标手势进行分割的结果如图3所示。

图3 较弱光照下基于深度信息的手势分割结果
在不同环境条件下,利用深度信息对目标手势进行分割的结果如图4所示。

图4 不同环境下基于深度信息的手势分割结果
从上述实验结果可知,在不同环境和不同光照条件下,本文所采用的方法依然可以准确地分割出目标手势,证明了本文方法的可靠性和优势。
1.2 手势质心计算
矩代表一幅图像或一个轮廓的全局特征,是描述图像特征的算子[16]。得到手势分割图像后,可计算出图像和轮廓的矩。
m00表示图像零阶矩,v(i,j)表示图像在点的灰度,(i,j)当图像为二值图像时,m00代表图像中白色区域的总和,因此可以用来求二值图像和轮廓的面积。如式(1)所示:

(1)
m10和m01表示图像的一阶矩,当图像为二值图像时,m10表示图像所有白色区域坐标的累加,m01表示图像所有白色区域坐标的累加。如式(2)、(3)所示:

(2)

(3)
再根据式(5),式(6):
(4)
(5)
就可得到目标区域即手势的质心点坐标(x,y)。最后绘制出轮廓的矩形边界。
利用图2(b)中的手势分割结果得到的手势轮廓矩形边界、零阶矩和一阶矩的值以及手势图像质心坐标如图5所示。

图5 矩形轮廓与手势质心坐标
当每帧手势图像传入时,都按照上述方法操作,得到每帧图像中的手势质心,这样便得到了一连串的手势质心点坐标。综上所述,完成手势质心计算。
1.3 手势轨迹特征计算
前文提到,动态手势识别关注的是手势轨迹信息,而不关注手形。本文要做的就是从连续的视频帧里得到动态手势的轨迹信息。当一个动态手势完成后,假设相邻两帧图像手势质心点坐标分别为(x1,y1)和(x2,y2),则每帧图像中的手势质心坐标结合在一起可以表示成一个手势质心轨迹p:
p=[(x1,y1), (x2,y2),…, (xi,yi)]
(6)
同时,每相邻两帧手势质心点连成的直线与水平方向都会形成一个角度,设该角度为θi:
(Δxi,Δyi)=(xx+1-xi,yi+1-yi)
(7)
则多个不同的θi可以组成个一维向量T:
T=[θi,θi+1,…,θi+n]
(8)
将一维向量T中的每个角度都利用链码进行编号,其中,θi的值决定了θi所在链码编号,依次类推。如此便可得到一个由链码编号组成的一维向量X,而X正是动态手势的轨迹特征。
如图6所示,链码[17]把一个平面平均分成了12个部分,并对这12个部分进行编号,编号分别为1~12。
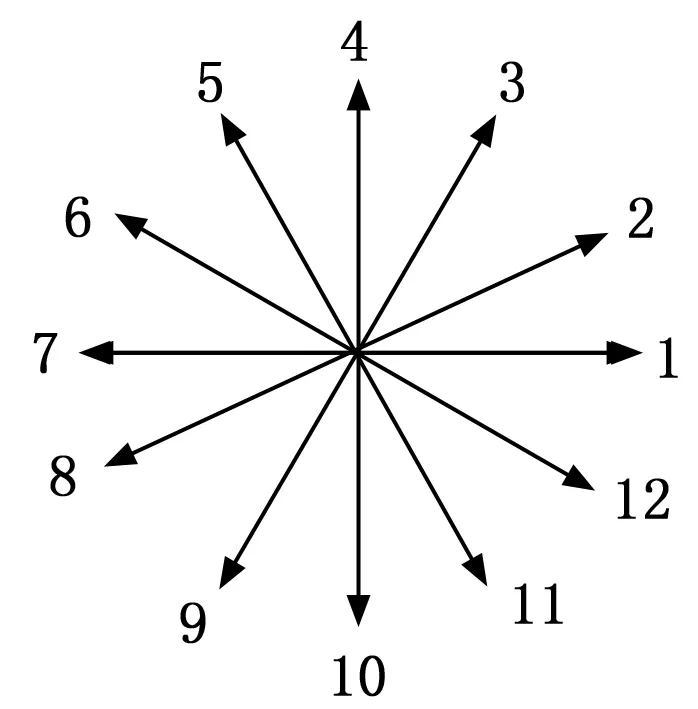
图6 链码示意图
设0~180°范围内,相邻编号所属直线之间的角度为30°。在0~-180°范围内,相邻编号所属直线之间的角度为-30°。
当平面被平分的部分越多,通过角度θi的值量化得到的编号越准确,则动态手势的轨迹特征越精确,所以这里将平面划分成12个部分。
例如,利用第一帧手势图像质心坐标点与第二帧手势图像质心坐标点计算出两点形成的直线与水平方向所成角度为,再比较是否在0~30°范围之内,若为0°则添加编号1到一维向量X中,若在0~30°之间,则添加编号2到一维向量X中。由此可以得到动态手势轨迹特征X。
本文选择其中稳定的6个手势质心点进行计算,则X的长度为5,即每个完整的手势轨迹特征由5个编号组成。
1.4 手势轨迹特征识别
在完成手势分割、手势质心与手势轨迹特征计算的基础上就可以进行手势轨迹特征识别。由于不同的人在做同一手势动作时速度不一样,所需的时间也不一样,则会造成每个人的手势起终点不确定。若要进行手势起终点判定则会加大计算量和复杂程度,影响效率。
而动态时间规整算法(DTW,dynamic time warping)则通过把手势轨迹特征进行延伸或缩短,来计算比较两个手势轨迹特征之间的相似性,所以采用DTW算法可以省去手势起终点的判定,并减少不同的人做相同手势时,手势轨迹特征不完全相同带来的影响。
假设给定两个序列:
X=[x1,x2,...xi],Y=[y1,y2,...yj]
(9)
其中:i=j。在本文中,X实际为得到的手势轨迹特征,Y为事先设定好的多个手势轨迹特征模板且每一个模板Y都拥有唯一序号。当X与Y之间的累积距离越小,则代表这两个序列越相似,即表示X与Y越吻合。
DTW算法的步骤如下:
1)构造一个i*j的距离矩阵M,M矩阵中元素(i,j)表示xi和yj两个点的距离d(i,j);
2)根据距离矩阵M生成累积距离矩阵N,生成N的方法为:矩阵N中第一行第一列的元素为M矩阵中第一行第一列的元素。矩阵N中其他位置的元素通过:
N(i,j)=Min(N(i-1,j-1),N(i-1,j),
N(i,j-1)+M(i,j)
(10)
计算得出;
3)矩阵N中最右上角的元素为累积距离Q。
举例说明:假设手势轨迹特征X=[3,5,6,7],模板Y=[4,3,2,6]现在要比较X和Y的相似程度,DTW会根据X与Y之间点到点的距离生成一个距离矩阵M,结果如下:
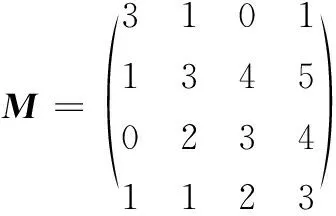
(11)
然后根据距离矩阵M生成累积距离矩阵N,结果如下:

(12)
由累积距离矩阵N中最右上角的元素可知,累积距离Q=4。
综上,当完成手势分割,手势质心和手势轨迹特征计算后,会得到一个一维的手势轨迹特征向量X,将X作为输入喂入DTW算法模型并依次与模型中的多个手势轨迹特征模板Y进行模板匹配,得到多个累积距离Q,将Q中最小值所属模板Y的序号作为输出结果,从而完成手势轨迹特征识别。
DTW算法[18-20]数据训练简单,结构简单明了易于实现,同时也省略了手势起终点的判定且识别准确率高。缺点是模板Y需要事先定义,且计算量随着模板的增多而加大。
2 实验验证与分析
2.1 实验硬件与软件
本文实验的硬件主要包括:显卡为GTX1050,内存为4 GB和处理器为i7的笔记本电脑、基于Kinect开发环境的传感器、一台六足机器人。
软件部分主要包括:PyCharm编译环境、开源计算机视觉库(OpenCV,open source computer vision library)、开放式的自然交互框架(OpenNI,open natural interaction)以及采用Python编写的手势识别算法。
2.2 实验流程
首先传感器采集用户动态手势视频序列,将视频序列传给上位机进行处理得到与该用户手势轨迹特征匹配的模板的序号,将该模板序号传给STM32,驱动板根据STM32计算得到的舵机数据进行六足机器人舵机控制,同时机器人自身传感器采集六足机器人状态,将状态信息发送至STM32,形成闭环控制,完成手势对六足机器人的控制。
2.3 实验
首先设定人机交互手势模板,如表1所示。该模板设计了4种动态手势指令分别控制机器人4种动作。该模板存储在DTW模型中,其中模板基于链码规则设定。

表1 自定义人机交互手势模板
现在要使机器人前进,则用户将手在六足机器人搭载的传感器前由左向右水平移动。
经过手势分割的移动过程如图7所示。

图7 动态手势移动分割图
经过上位机处理得到如下6个手势质心坐标和手势轨迹特征X=[1,2,1,2,1],如图8所示。

图8 质心坐标与手势轨迹特征
随后X将被送入DTW模型中与已经建立好的多个模板Y进行匹配,匹配结果如图9所示。
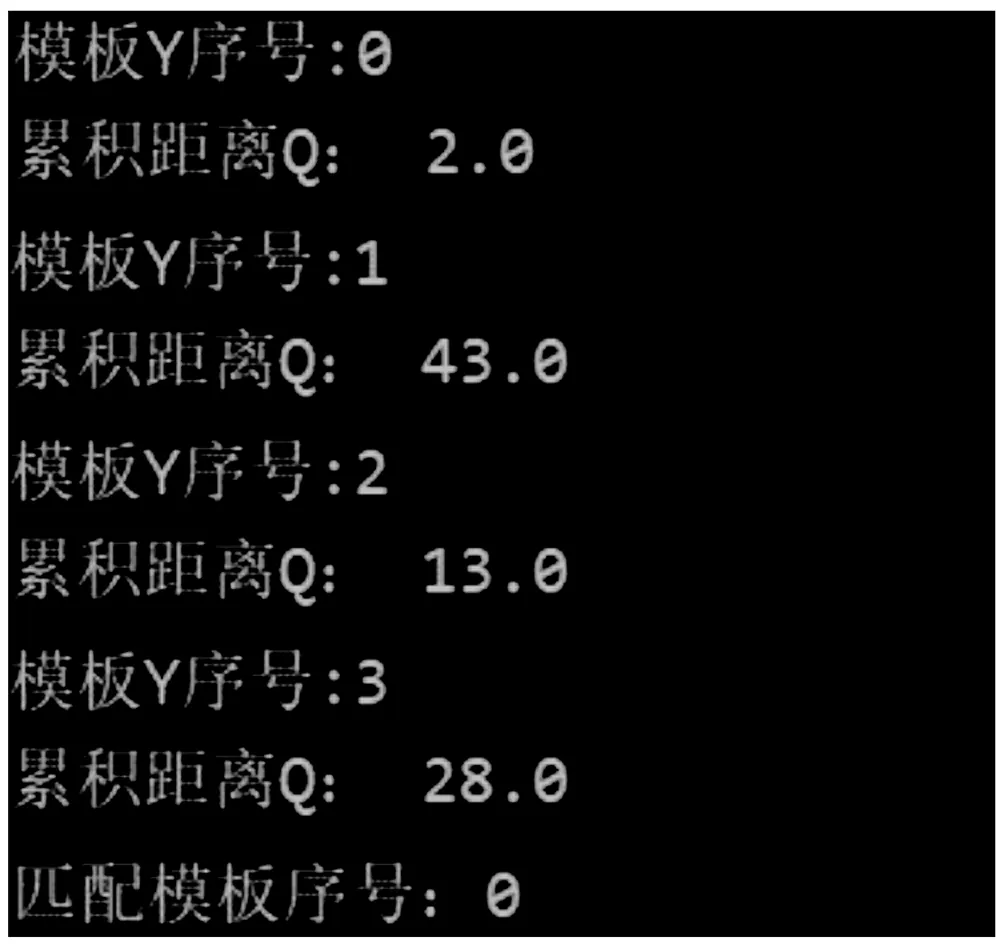
图9 匹配结果
由图9可知,X与序号为0的模板累积距离为2,X与序号为1的模板累积距离为43,X与序号为2的模板累积距离为13,X与序号为3的模板累积距离为28。
经过筛选最终得到了与X累积距离最小的模板:序号为0,累积距离Q=2。即手势轨迹特征X=[1,2,1,2,1]与模板Y=[1,1,1,1,1]最相似吻合。
将该模板序号数字0通过无线传输设备传给STM32分析处理语义信息,再由STM32向六足机器人传输指令控制六足机器人的行动轨迹。以图10中黑色叉为标记,采用前进手势进行交互时,六足机器人完成前进动作。

图10 人机交互结果
本文在不同环境和不同光照条件下进行了多次动态手势识别实验,得出结果如表2~4所示。

表2 室外光照识别结果

表3 室内较强光照识别结果

表4 室内较弱光照识别结果
实验结果表明,在室内较强光照条件下,手势识别效果比较弱光照条件下好,最好的识别准确率能达到97.3%。在室内较弱光照条件下,准确率仍然能达到91%及以上。在室外的手势识别效果不如室内,但准确率依然能达到90%左右。由此可知在外部环境变换的情况下,该方法依然能保持一个较好的识别准确率,也证明了整个动态手势识别方法的鲁棒性较好。
3 结束语
综上所述,本文基于Kinect传感器对动态手势识别进行了研究。利用深度信息分割出目标手势,此方法不易受环境和光照的干扰。基于矩和链码计算出手势质心和手势轨迹特征。在手势轨迹特征识别部分,传统方法大多数采用隐马尔可夫模型,但该方法训练非常困难和复杂,同时要进行手势起始点判定。所以采用训练简单、结构易懂、识别准确率高的DTW算法并且避免了手势起始点判定,该算法缺点是不能识别模板中没有的手势。最后将手势识别结果与六足机器人进行交互,实现动态手势对六足机器人的控制。
