不同直径比管道车运移时的水力特性

摘 要：筒装料管道水力输送作为一种新型管道水力输送技术，通过在料筒两端分别安装带有万向滚珠的支撑，成功解决了料筒在管道中的悬浮问题并降低了磨损。以直径比为0.5、0.6、0.7、0.8的管道车为研究对象进行试验分析。结果表明：对于既定的管道，流量存在一个阈值Q中，当流量小于阈值时，管道车的平均速度随直径比的增大而增大，当流量大于阈值时，随着直径比的增大，管道车的平均速度表现为先减小后增大的变化趋势，在直径比为0.6左右时，管道车的平均速度最小;管道车在载荷、流量、车长和导流条安放角等参数一定的条件下，随着直径比的增大，总能耗表现为先减小后增大的趋势，总能耗最小值出现在直径比为0.6的工况附近。

关键词：直径比;管道车;水力输送;水力特性

中图分类号：TV134.2文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.01.025

引用格式：郭亚丽.不同直径比管道车运移时的水力特性[J].人民黄河，2021，43（1）：129-132.

Hydraulic Characteristics of Piped Carriages with Different Diameter Ratios During Transportation

GUO Yali

（Taiyuan Urban Vocational College， Taiyuan 030027， China）

Abstract：As a new technique of the piped hydraulic transportation， the piped hydraulic transportation of tube-contained raw material， one brace with a universal ball bearing installed at the bottom at each side of the barrel is installed， solves the suspension of the container in the pipeline and reduces abrasion. Based on the different diameter ratios， the experiment on the piped carriages was analyzed. The results show as follows. For the established channel， there is a flow threshold， when the flow is less than the flow threshold， the average speed of the piped carriage is increased along with the diameter ratio， when the flow is greater than the flow threshold， the average speed of the piped carriage is firstly decreased along with the increase of the diameter ratio， then increased， the lowest value occurs around the diameter ratio of 0.6; In any case change of the piped carriage， under the same load， flow， length of the piped carriage and diversion angle of the guide vanes， the total energy consumption value shows the trend is firstly decreased and then increased， the total energy consumption minimum value appear in the pipes near the operation condition of the diameter ratio of 0.6. These conclusions will provide an important reference for improving the technical parameters of the piped hydraulic transportation technique.

Key words： diameter ratios; piped carriage; hydraulic transportation; hydraulic characteristics

1 引 言

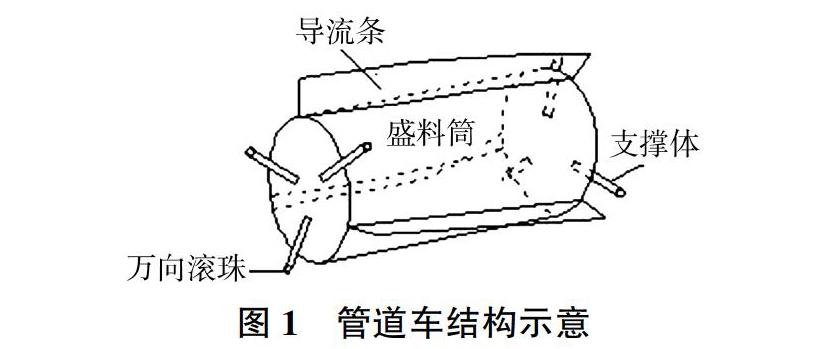
在型料管道水力輸送的基础上提出的筒装料管道水力输送技术[1]，是将物料装在管道车内（一般为圆形料筒），依靠水流的推力作用，推动管道车在管道中运移，将物料输送到目的地的一种新型输送方式。管道车是该输送技术的物料输送载体，为保证其在有压管道中的低能耗稳定运行，将其结构设计成带导流条的圆柱体与带滚珠的圆柱支撑体组合而成的组合体[2-3]，成功解决了料筒在管道中的悬浮问题并降低了磨损。管道车结构如图1所示。

管道车在管道中运移时的车速、管道内流场分布以及压力变化等均受多种因素影响，如直径比、流量、输送物料的质量以及管道车的结构等，许多学者对此进行了大量的试验研究及理论分析。李永业等[4-5]假设管道车在管道内平稳移动并具有足够的刚度，建立了管道车在湍流中运动的数学模型，通过试验对数学模型进行了测试，研究结果表明管道车辆速度的计算值在各种影响因素变化的情况下与试验值相同。胡志毅等[6]对不用荷重条件下的管道车概化圆柱体模型进行了研究，结果表明管道车的运移速度和荷重为负相关关系，且随着输送荷载的增大，管道内的能耗损失呈现出逐渐增大的趋势。张雪兰等[7]研究了多个管道车串联布置运行时的环隙水流特性，分析了环隙水流的沿程流速及压力分布规律。Taimoor Asim等[8-9]通过数值模拟研究了圆柱形输送体在管道水力输送中的输送特性，分析了不同长度圆柱形输送体的运动速度及管内水流的压强和流速变化规律。Deniz Ulusarslan等[10-11]研究了低密度球形输送体在输送中流体的局部水头损失系数及管道内流体的压力梯度，分析了在输送体运动速度相同的条件下，管道内流体的压力梯度与输送体密度的变化关系，得出了输送体的运动速度越大，压力梯度就越接近1;90°弯管流体的压力梯度高于45°弯管的，而且在相同流速和相同输送体密度条件下，90°弯管流体的局部损失是45°弯管的2～3倍。Zhang Chunjin等[12]采用双向耦合的方法对不同安放角条件下带导叶的管道车运移时的环状缝隙流场水力特性进行了数值模拟计算。Zhang Xuelan等[13-14]运用数值模拟的方法对不同流量条件下的二维和三维环状缝隙流速度和压力分布进行了研究。目前对影响管道车运移时水力特性的因素的研究多集中在雷诺数、荷重、导流条安放角等，随着研究的深入，逐渐对直径比展开研究。所谓直径比指管道车外径d与管道内径D的比值，管道车外壁与管壁之间形成的环状缝隙宽度由直径比决定，而环状缝隙宽度的变化，不仅会对环状缝隙内流场的分布产生影响，还会影响管道车前后端面和车身的受力分布。因此，笔者通过对不同直径比条件下管道车运移时的水力特性进行研究，以期对提高管道车运移速度、降低管道车运移时的能耗损失，以及加快管道车的实际生产应用提供参考。

2 试验系统及测点布置

2.1 试验系统

试验系统主要由流量调控系统、管道车的加入与回收系统、输送管道组成。其中：输送管道由有机玻璃圆管组成，管道内径为100 mm，流量调控系统由涡轮流量计配合闸阀组合而成，管道车的加入装置为一喇叭状的垂直管道，管道车的回收装置为一矩形水箱。试验时，通过水泵将水流从蓄水池抽入输送管道，然后利用流量调控系统将流量调节至试验所需范围，等到管道内水流稳定后，在有压水流的作用下管道车开始运动，当管道车经过试验测点时，记录其运动时间和管道内压力变化情况，最后通过管道车回收装置对管道车进行回收，水流则流入蓄水池，形成完整的闭合循环回路。这其中，管道内水流的压力采用压力传感器测量，管道车的运动速度采用光电传感器测量，试验数据采集通过无纸记录仪来完成。整个管道的长度除以管道车在管道内运移的总时间即管道车的平均速度。试验系统示意见图2。

2.2 测点布置

共布置10个压力测点（1#～10#），各测点的位置见图2，沿水流方向各测点与投放装置的距离见表1。

2.3 试验方案

本文主要研究不同直径比对管道车运移时水力特性的影响，选定试验管道车d=50、60、70、80 mm，从而得到直径比分别为0.5、0.6、0.7、0.8，选用管道车车长为100 mm和150 mm，对应导流条长度l为100 mm和150 mm，导流条参数参照机翼的结构对流体的升力与阻力的影响来选取，安放角θ选定10°、15°，高度h=0.6（D-d）/2，导流条厚为3 mm。管道车输送质量G为1 150 g和1 250 g，在流量Q=30～90 m3/h范围内进行试验。

3 试验结果与分析

3.1 不同直径比条件下管道车平均速度的变化

管道车车长L=100 mm和150 mm、导流条长度l=100 mm和150 mm、导流条安放角θ=15°时，管道车平均速度与直径比的关系如图3所示。

（1）从总体来看，对于该试验，存在一個约为70 m3/h的流量阈值Q中，其可作为直径比与管道车平均速度关系的一个分界点。

（2）当流量Q

（3）当流量Q>Q中时，随着直径比的逐渐增大，管道车的平均速度呈现出先

减小后增大的变化趋势，只是下降幅度不大，在d/D=0.6左右出现最低点，之后随直径比的增大，管道车平均速度又逐渐增大。当d/D<0.6时，管道车直径较小，使得前后端面以及侧面积都较小，管道车受到的推力相对较小，故随直径比增大而增大的量相对有限，而属非流线型物体的管道车此时受到的总绕流阻力等随直径比增大而增加明显，故合力有所减小，管道车运移平均速度稍微下降。当d/D>0.6时，管道车运行的平均速度又呈现增大趋势，其原因主要是直径比增大使得管道车运行的总动力增大。

3.2 不同直径比条件下管道能耗变化

假设管道车在管道内平稳运移，其平均运移速度为v，在运移管道车车身上建立相关坐标系，则管道内水流相对于管道车的速度为v1-v。依据车体建立的坐标系，水流在流经运动管道车前后断面的能量平衡方程可表示为

Z1+p1γ+α1（v1-v）22g=Z2+p2γ+α2（v1-v）22g+Δhw（1）

式中：Z1、Z2分别为管道车前、后断面水流的位置水头;p1γ、p2γ分别为管道车前、后断面水流的压强水头;α1（v1-v）22g、α2（v1-v）22g分别为管道车前、后断面水流的流速水头;v1为管道中水流的平均流速。

当流量一定时，管道内径不发生变化，且取α1=α2=1，则式（1）表示为

Δhw=（Z1+p1γ）-（Z2+p2γ）（2）

由式（2）可知，管道车在管道内运移时整个管路的水头损失等于管道车前后两端面的测压管水头差。因此，试验过程中通过压力传感测得各测点的测压管水头值，利用式（2）即可计算出管道车在管道内运移时的水头损失。

图4为车长L=100 mm、导流条长l=100 mm、安放角θ=10°、G=1 150 g和1 250 g条件下，流量分别为50、80 m3/h时，管道车在管道内运移时的总水头与直径比的关系。

（1）在同一工况条件下，管道车运移时总水头损失随直径比的变化趋势大致相同，即随着直径比的增大，总水头损失先呈现出逐渐减小的变化趋势，当直径比为0.6左右时，其最小，之后随着直径比的增大，其呈现出逐渐增大的变化趋势，说明直径比是影响管道车运行时车前后两端面的水头损失和环隙水流紊动损失的关键因素。

当直径比d/D<0.6时，流量一定，直径比越小，管道车直径越小，管道车与管壁所形成的环状缝隙宽度越大，环状缝隙流流速值减小，同时车体两端面及侧面受力面积也减小，受到的轴向向前推力相应越小，水流动力有效利用率越低，从而输送总水头损失增大。

当直径比d/D>0.6时，随着直径比的增大，管道车直径变大，车体周围环状缝隙减小，缝隙流流速增大，虽然水流能量转化为车体运动能量的效率增大，但此时缝隙流流速的增大导致车体侧面与管壁间局部水头损失急剧增大，由于管道车运行过程中车后会不同程度地产生旋涡，因此涡体从产生到衰减直至消失也伴随着一定程度的能量损失。这些都是使输送总水头损失随着直径比的增大表现为增大趋势的重要原因。

当流量Q>Q中时，在管道内流量、输送物料荷重、车身长度以及导流条长度、厚度、安放角等因素不变的情况下，管道车平均速度在直径比d/D=0.6左右出现最低点，即管道车获得的动能最小，这也是能耗值在直径比d/D=0.6左右出现最小值的一个重要因素。

因此，在管道车工业化应用过程中可以把直径比作为管道车低能安全运行工况优选的重要控制参数。

（2）在输送工况一定时，随着管道内流量的不断增大，管道车运移时总水头损失也增大。在输送流量、直径比、车身长度以及导流条长度、厚度、安放角一定时，管道车运行的总能耗随着输送物料荷重的变化而变化，说明输送物料荷重也是影响能耗的一个重要因素。

4 结 论

通过对不同直径比条件下管道车运动时的水力特性进行研究，得出如下结论：

（1）当流量Q

（2）当流量Q>Q中时，随着直径比的增大，管道车的平均速度表现为先减小后增大的變化趋势，在直径比为0.6左右时，管道车的平均速度最小。

（3）管道车在输送物料载荷、流量、管道车车长和导流条长度、厚度、安放角等参数不变的条件下，随着直径比的增大，总能耗呈现出先减小后增大的趋势，且在直径比d/D=0.6左右出现最小值。

因此，直径比是影响管道车运移的一个重要因素，适当地选取直径比既可以提高运输速度，又能尽量降低能耗，提高运输的效率。

参考文献：

[1] 张雪兰，孙西欢，李永业.筒装料管道水力输送环隙流场特性试验研究[J].重庆交通大学学报（自然科学版），2014，33（1）：75-78.

[2] 王锐，孙西欢，李永业.管道车在不同雷诺数条件下的输送特性[J].排灌机械工程学报，2011，29（4）：343-346，358.

[3] 井元昊，郭向红，孙西欢，等.管道车环状缝隙流水力特性[J].水电能源科学，2014，32（7）：151-155.

[4] 李永业，孙西欢，阎庆绂，等.不同导流条安放角条件下筒装料管道水力输送试验研究[J].水动力学研究与进展A辑，2008，23（1）：86-89.

[5] 李永业，孙西欢，延耀兴.管道车不同荷重时筒装料管道水力输送特性[J].农业机械学报，2008，39（12）：93-96.

[6] 胡志毅，李永业，黄莹彬.不同荷载圆柱体在压力管道中运输的水力特性研究[J].长江科学院院报，2018，35（11）：86-90.

[7] 张雪兰，孙西欢，李永业.筒装料管道水力输送动边界流压力特性[J].排灌机械工程学报，2014，32（3）：231-234，241.

[8] TAIMOOR Asim， RAKESH Mishra. Computational Fluid Dynamics Based Optimal Design of Hydraulic Capsule Pipelines Transporting Cylindrical Capsules[J].Powder Technology，2016，295（7）：180-201.

[9] TAIMOOR Asim， RAKESH Mishra， SUFYAN Abushaala， et al. Development of a Design Methodology for Hydraulic Pipelines Carrying Rectangular Capsules[J]. International Journal of Pressure Vessels and Piping， 2016， 146（10）：111-128.

[10] DENIZ Ulusarslan. Comparison of Experimental Pressure Gradient and Experimental Relationships for the Low Density Spherical Capsule Train with Slurry Flow Relationships[J]. Powder Technology， 2008， 185（2）：170-175.

[11] DENIZ Ulusarslan. Experimental Investigation of the Effect of Diameter Ratio on Velocity Ratio and Pressure Gradient for the Spherical Capsule Train Flow[J]. European Journal of Mechanics B/Fluids， 2013，37（1）：42-47.

[12] ZHANG Chunjin， SUN Xihuan， LI Yongye， et al. Effects of Guide Vane Placement Angle on Hydraulic Characteristics of Flow Field and Optimal Design of Hydraulic Capsule Pipelines[J].Water，2018，10（10）：1378.

[13] ZHANG Xuelan， SUN Xihuan， LI Yongye. 3D Numerical Investigation of the Wall-Bounded Concentric Annulus Flow Around a Cylindrical Body with a Special Cylinders Array[J]. Journal of Hydrodynamics，2015，27（1）：120-130.

[14] ZHANG Xuelan， SUN Xihuan， LI Yongye， et al. Numerical Investigation of the Concentric Annulus Flow Around a Cylindrical Body with Contrasted Effecting Factors[J]. Journal of Hydrodynamics，2015，27（2）：273-285.

【责任编辑 张华岩】