集对多粒度水体富营养化评价模型构建与验证

张春英 高瑞艳 冯晓泽

摘 要：为了满足用户进行水体富营养化评价时的不同需求，针对水体富营养化评价中各评价指标的多样性和不确定性，综合考虑指标的多粒度特性，运用集对信息粒计算方法构建多粒度水体富营养化评价模型。首先，分级别建立样本各个指标的集对关联度，根据正同度最大和负反度最小的等级，计算评价确定度;其次，计算各个指标的信息熵，根据熵的大小确定评价指标的重要度，分析不同指标子集下不同粒度的评价确定度，构建多粒度的水体富营养化评价模型;最后，以我国12个代表性湖库为实例对模型进行了验证，并与Gamma-云方法、改进粗-云方法、模糊可变集法、单一指标法、神经网络法以及投影寻踪法的评价结果进行了对比，结果表明该模型可以客观反映水体的实际状况，适用性更强。

关键词：水体富营养化评价;集对分析;集对信息粒;属性重要度;多粒度评价

中图分类号：X824;TV213.4文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.01.016

引用格式：张春英，高瑞艳，冯晓泽.集对多粒度水体富营养化评价模型构建与验证[J].人民黄河，2021，43（1）：82-88.

Construction and Validation of Evaluation Model for Eutrophication of

Set Pair Multi-Granularity Water Bodies

ZHANG Chunying1，2， GAO Ruiyan1， FENG Xiaoze1

（1.College of Science， North China University of Science and Technology， Tangshan 063210， China;

2.Key Laboratory of Data Science and Application in Hebei Province， Tangshan 063210， China）

Abstract： In order to meet the different needs of water eutrophication evaluation， in view of the diversity and uncertainty of each evaluation index in the evaluation of eutrophication of water body， considering the multi-granularity characteristics of the index， the evaluation model of eutrophication of multi-granularity water bodywas constructed by using the set pair information particle calculation method. Firstly， the set pair correlation degree of each index of the sample was established at different levels. The evaluation determination degree was determined according to the grade with the maximum positive degree and the smallest negative degree. Secondly， the information entropy of each index was calculated. The importance of the evaluation index was determined according to the entropy. The evaluation determination degree of different granularity under different index subsets was analyzed and the multi-granularity evaluation model of water eutrophication was constructed. Finally， the model was verified with 12 representative lake reservoirs in China and compared with the evaluation results of Gamma-Cloud method， improved rough cloud method， fuzzy variable set method， single index method， neural network method and projection pursuit method， the validity of the model was verified. The results show that the model can reflect the actual situation of water body more objectively and has stronger applicability.

Key words： water eutrophication; set pair analysis; set pair information granular; attribute importance; multi-granularity evaluation

水資源是人类社会发展不可或缺的重要资源之一，当前存在的水资源污染问题不仅阻碍了社会经济的发展，而且对海洋生物的生存造成了很大冲击，因此解决水资源污染危机刻不容缓。水体质量评价方法包括单因子评价法[1]、内梅罗指数法[2]、模糊综合评价法[3-4]、灰色聚类法[5]、人工神经网络评价法[6]等。单因子评价法虽然计算简便，易推广，但是其将最差指标对应的水质类别作为最终评价结果，往往与实际情况存在一定偏差。内梅罗指数法应用广泛，但过分突出极大值对评价结果的影响，不能对所有指标进行综合评价。模糊综合评价法通过隶属函数，对被评价对象的隶属等级进行综合评价。灰色聚类法推导过程严谨，但需要主观选择白化函数，确定聚类权。人工神经网络评价法较其他方法具有高速计算能力，但不能确定主要污染组分以及各个指标的污染程度。

水资源评价过程主要是不确定性问题的处理[7-8]。集对分析[9]是一种新的研究确定性和不确定性系统的理论，已应用于生态系统健康评价[10]、航空航天风险评估[11]、水闸运行安全态势综合评判[12]、综合承载力预测[13]等领域。水体富营养化评价指标具有多样性，以往评价方法大多基于确定的指标进行水体富营养化评价，极少考虑指标的多粒度特性。集对分析是基于同一粒度对系统进行确定-不确定分析。集对信息粒[14]是在粒计算方法基础上，结合集对关联理论的成对原理、层次性原理和信息完整性原理提出的一种新的粒计算模型，能够描述粒空间中的确定-不确定信息，完整表达信息粒的结构。该方法是将问题W=（U，A，V）与子问题W0=（U0，A0，V0）形成集对，在二元关系R下，分析W0相对W的正同、负反与差异程度。集对粒用（Xc，Xu）表示，其中：Xc称为确定粒，由（Xcs，Xco）构成，Xcs为正同粒，Xco为负反粒;Xu为差异粒，是不确定粒。集对粒是模糊粒、粗糙粒的拓展，是模糊粒、粗糙粒的一般表示形式。根据用户分析问题时选取的不同粒度构造出不同粒度下的分析模型，使得综合决策更加符合客观实际需求。笔者从水体富营养化评价指标的多粒度、多层次出发，运用集对信息粒方法，选取不同评价指标集构建多粒度评价模型，综合考虑多粒度下的评价结果，得到最终评价结果。

1 模型构建

1.1 评价参数与指标的确定

根据《地表水环境质量标准》（GB 3838—2002）以及水体富营养化评价指标选取原则，选取Chla（叶绿素a）、TP（总磷）、TN（总氮）、COD（高锰酸盐指数）、SD（透明度）5个参数进行集对多粒度水体富营养化评价。湖库富营养状态分为6级，分别为Ⅰ级-贫营养、Ⅱ级-贫中营养、Ⅲ级-中营养、Ⅳ级-中富营养、Ⅴ级-富营养和Ⅵ级-重富营养。根据舒金华[15]的研究结果，我国湖库富营养化评价指标的评价标准见表1。

1.2 指标集标准化

X=（apq）mn为m个样本、n个评价指标的实测值组成的矩阵，将其进行标准化处理，得到标准化矩阵X*=（xpq）mn。

xpq=apq-（apq）min（apq）max-（apq）min （越大越优型）（apq）max-apq（apq）max-（apq）min （越小越优型）（1）

式中：apq为实测值;（apq）max、（apq）min分别为第q个评价指标的最大值、最小值。

1.3 属性重要度计算

水体富营养化评价是一种多指标的综合评价，必须确定各个指标的属性重要度。本文采用信息熵[16-17]的原理和方法计算指标的属性重要度，信息熵越小，说明各样本点的某指标实测值的差异越大，该指标在水体富营养化评价中所起的作用越大。根据斯梯林公式[18]，第q个评价指标的信息熵eq为

eq=-1ln m∑mp=1Zpqln ZpqZpq=xpq/∑mp=1xpq（2）

式中：0≤Zpq≤1，当Zpq=0时，Zpqln Zpq=0。

1.4 集对关联度[14]计算

定义1。设W=（U，A，V），W0=（U0，A0，V0），A0A，V0V，R为U上的一个二元关系，定义W上一对子集Xc={Xc1，Xc2，…，Xcm}、Xu={Xu1，Xu2，…，Xun}分别为确定信息粒和不确定信息粒，则对于信息x∈W0，存在一对映射

τXc： W0→[0，1]，x→τXc（x）=aR+cR

τXu： W0→[0，1]，x→τXu（x）=bR

其中，aR+cR和bR分别为x关于Xc、Xu的确定度和不确定度。

定义2。基于确定信息粒Xc，RA0，定义Xc上一对子集Xcs={Xcs1，Xcs2，…，Xcsk}、Xco={Xco1，Xco2，…，Xcot}为正同信息粒和负反信息粒，则对于信息x∈Xc，存在一对映射

τXcs： Xc→[0，1]，x→τXcs（x）=aR

τXco： Xc→[0，1]，x→τXco（x）=cR

其中，aR、cR分別为x关于Xcs、Xco的正同度和负反度。

定义3。W=（U，A，V），W0=（U0， A0， V0），A0A，V0V，则按定义1和定义2，形成集对（W0，R）归结为一个完整的集对关联度：ρ（W0，R）=aR+bRi+cRj，其中i∈[-1，1]、j=-1，分别称为差异度和负反度标记符号，用以识别分类信息的方向和不确定程度。

针对水体富营养化评价，在问题空间W=（U，A，V）中，U表示待评价的样本集空间，A表示指标集空间，V表示U关于A的值域数据空间。动态选取不同指标集，可形成多个子空间W0，其中A0A，V0V。对每个子空间进行集对关联度计算，得到各个样本在不同等级下的正同度、差异度以及负反度，根据最大正同度所在的等级确定样本的评价结果，若存在正同度相同的情况，则增加负反度进行分析，选择负反度最小的等级作为评价结果，由此形成多粒度的评价模型。对于评价结果，可能是一个确定的等级也可能有多个等级，具有多个等级的评价结果可以用区间形式表示，也可以根据实际情况添加评价指标，进一步分析计算获得一个确定的评价等级。

设评价指标为vq（q=1，2，…，n），待评价样本为xp（p=1，2，…，m），在不同指标下，样本xp的隶属等级us取值为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ和Ⅵ。选取评价指标集A0形成子问题空间W0，对评价样本xp在各个等级下进行集对关联度计算，相同等级的作为正同粒，相邻等级的作为差异粒，其他等级的作为负反粒，得到集对关联度：

ρ（xp，us）=SN+QNi+PNj（3）

式中：S、Q、P分别为正同粒、差异粒、负反粒的个数;N为信息粒的总个数。

令SN=a，QN=b，PN=c，其中a、b、c分别为正同度、差异度、负反度，则式（3）可简化为

ρ（xp，us）=a+bi+cj（4）

根据属性重要度的大小，去掉冗余指标（属性重要度最小的指标），形成新的评价指标集，从而得到新的子空间W0，对新的子空间运用式（3）再次进行上述集对关联度计算，从而得到该评价指标集下的评价结果。该过程可根据用户分析问题时选取的粒度多次循环计算，通过指标的动态选取，得到不同粒度下的评价等级，对比分析不同粒度下的评价结果，从而得到最终的评价结果。

集对多粒度水体富营养化评价流程见图1。

2 模型验证

2.1 数据来源与样本指标集等级分类

将集对多粒度水体富营养化评价模型应用于我国12个代表性湖库，12个湖库Chla、TP、TN、COD、SD实测数据[15]见表2，其中Chla、TP、TN、COD为越小越优型指标，SD为越大越优型指标。根据表1所列我国湖库富营养化评价标准，对表2实测数据进行富营养化分类，结果见表3。

2.2 样本指标集标准化

根据表2中的实测值得到矩阵X=（aij）mn，对其进行标准化处理，得到标准化矩阵X*：

X=1.000.840.991.001.000.991.001.000.850.800.980.960.950.700.460.940.990.950.720.360.940.900.910.780.180.950.830.870.780.040.710.830.880.590.070.690.550.840.010.120.640.830.870.350.080.230.000.580.440.060.000.300.000.090.000.300.060.560.000.04

2.3 属性重要度计算

将X*中数据代入式（2），计算得到各个评价指标的信息熵，eChla=0.935 4、eTP=0.921 0、eTN=0.958 9、eCOD=0.890 0、eSD=0.755 1，即5个指标的重要程度从高到低依次为SD、COD、TP、Chla、TN。

2.4 集对关联度计算

根据表3所列湖库富营养化等级，对12个湖库水体富营养化程度进行集对关联度计算。

（1）综合考虑5个指标，计算集对关联度。此时，N=5，分别计算得到S、Q、P的值，即可得到集对关联度。S为正同粒的个数，正同粒由相同等级确定;Q为差异粒的个数，差异粒由相邻等级确定;P为负反粒的个数，负反粒由其他等级确定。对于这12个样本，在水体富营养化评价的6个等级下，分别计算相同等级个数、相邻等级个数、其他等级个数，确定S、Q、P的值，进而求得正同度a、差异度b、负反度c。根据正同度、负反度分析确定评价结果，见表4。通过集对关联度计算得到各个湖库水体富营养化评价结果。邛海和洱海富营养化程度为Ⅲ级;博斯腾湖为Ⅳ级;于桥水库、磁湖、巢湖和甘棠湖为Ⅴ级;磨菇湖、杭州西湖、南京玄武湖、武汉墨水湖和广州东山湖为Ⅵ级。

（2）考虑4个指标，计算集对关联度。根据属性重要度的计算结果，去掉重要度最小的指标TN，只考虑SD、COD、TP、Chla这4个指标计算集对关联度，此时N=4，计算得到的集对关联度见表5。由表5可知，当去除TN这个指标时，洱海的富营养化程度从Ⅲ级转变为Ⅲ级或Ⅳ级，于桥水库的富营养化程度从Ⅴ级转变为Ⅳ级或Ⅴ级，其余湖库评价结果未发生变化。洱海的评价结果向下一等级转变，于桥水库的评价结果向上一等级转变，说明这两个湖的评价结果在用户不同需求下是会发生变化的。

（3）考虑3个指标，计算集对关联度。只考虑SD、COD、TP这3个指标，此时N=3，集对关联度评价结果见表6。当同时去除TN、Chla這2个指标时，相对于只去除TN这一个指标，洱海的富营养化程度从Ⅲ级或Ⅳ级转变为Ⅲ级，于桥水库的富营养化程度从Ⅳ级或Ⅴ级转变为Ⅳ级，其余未发生变化。

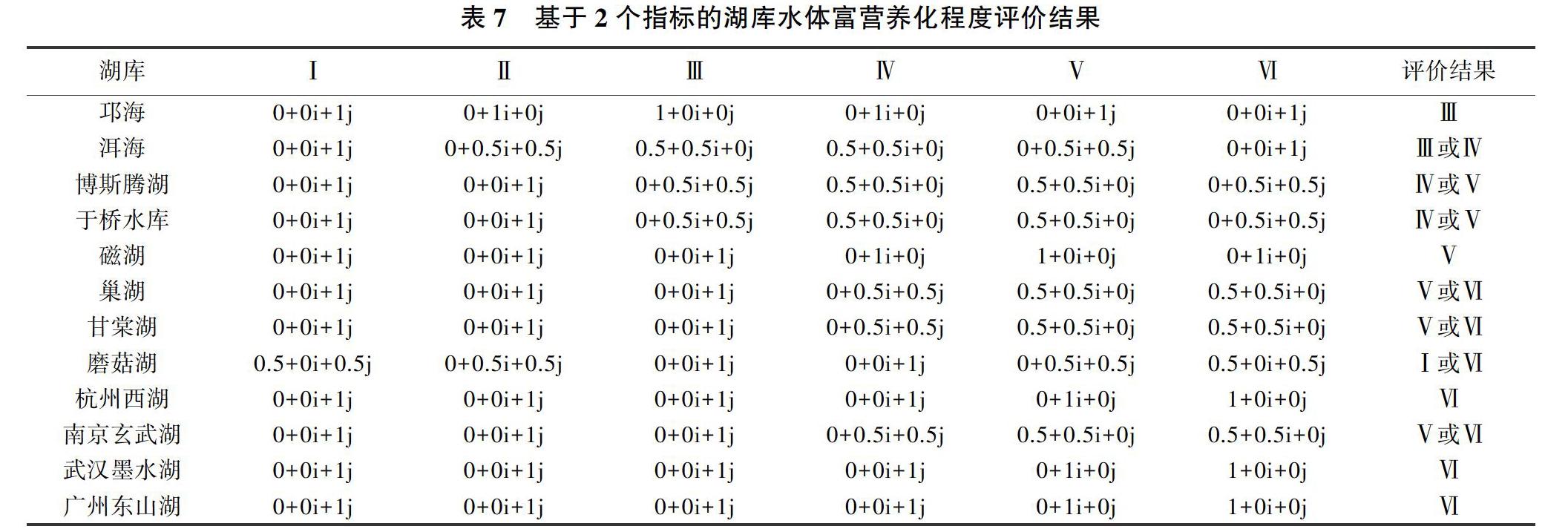
（4）考虑2个指标，计算集对关联度。只考虑SD、COD这两个指标，此时N=2，得到的集对关联度评价结果见表7。当同时去除TN、Chla、TP这3个指标时，相对于只去除TN、Chla这2个指标，洱海的富营养化程度从Ⅲ级转变为Ⅲ级或Ⅳ级，博斯腾湖的富营养化程度从Ⅳ级转变为Ⅳ级或Ⅴ级，于桥水库的富营养化程度从Ⅳ级转变为Ⅳ级或Ⅴ级，巢湖的富营养化程度从Ⅴ级转变为Ⅴ级或Ⅵ级，甘棠湖的富营养化程度从Ⅴ级转变为Ⅴ级或Ⅵ级，蘑菇湖的富营养化程度从Ⅵ级转变为Ⅰ级或Ⅵ级，南京玄武湖的富营养化程度从Ⅵ级转变为Ⅴ级或Ⅵ级，这7个湖的评价结果从一个确定的等级变成了具有多个等级的模糊等级，其中蘑菇湖的变化很大，说明指标过少会影响评价结果。

综上所述，通过指标集的动态变化，可以得到不同粒度下的评价结果。评价结果表明有些湖库从一个确定的等级变为具有多个等级的模糊等级，有些未发生变化，也有些从具有多个等级的模糊等级变为一个确定的等级。这些变化说明，评价结果不是固定不变的，当用户分析问题时选择的角度不同，选择的评价指标不同，得到的评价结果也会不同，另外，指标过少也会对评价结果造成影响。水体富营养化评价指标是多样性的，以往的水体富营养化评价方法大多基于确定的评价指标，而极少考虑指标的多粒度特性。集对分析是基于同一粒度对系统进行确定-不确定分析的，实际上人们往往会站在不同粒度、不同视觉对事物进行观察分析，综合得出最后结论或给出评价结果。本文提出的多粒度水体富营养化评价模型考虑了指标的动态变化，可以得到不同粒度下的评价结果，再综合考量得到最终评价结果。表4～表7展现了12个湖库在不同指标集下评价结果的变化，其中于桥水库在2个、4个和5个评价指标的情况下评价结果均为Ⅴ级，综合考量不同指标集下的评价结果，将评价等级确定为Ⅴ级，但通过多粒度评价结果可分析出，于桥水库的评价等级有向上一等级转化的趋势;洱海、博斯腾湖、巢湖和甘棠湖的评价等级依次为Ⅲ、Ⅳ、Ⅴ、Ⅴ级，但它们都有向下一等级转化的趋势;其他湖库在不同指标集下的评价结果几乎未发生变化，邛海、磁湖、蘑菇湖、杭州西湖、南京玄武湖、武汉墨水湖、广州东山湖的评价结果依次是Ⅲ、Ⅴ、Ⅵ、Ⅵ、Ⅵ、Ⅵ、Ⅵ级。

2.5 不同评价方法结果对比

为了验证该模型的有效性，选取了Gamma-云方法[19]、改进粗-云方法[20]、模糊可变集法[21]、单一指标法、神经网络法[22]以及投影寻踪法[23]6种方法与集对多粒度水体富营养化评价模型得到的评价结果进行对比，见表8。

（1）邛海在不同粒度下的评价结果均为Ⅲ级，故将其评价等级确定为Ⅲ级，与Elman法评价结果一致，但比其他方法得出的水体富营养化等级高，由于正态云方法未充分考虑COD的影响，单一指标法将指标的最高等级作为评价结果，因此评价结果存在一定偏差，将评价结果确定为Ⅲ级是合理的。洱海和博斯腾湖的评价等级分别确定为Ⅲ级、Ⅳ级，但其均有向下一等级转化的趋势，应注意湖库水环境的保护。于桥水库、磁湖、巢湖和甘棠湖等局部出现水华，评价等级确定为Ⅴ级，其他评价方法中多数方法也将这4个湖的评价等级确定为Ⅴ级。磨菇湖、杭州西湖、南京玄武湖、武汉墨水湖、广州东山湖出现水华，严重影响旅游和水产养殖业的发展，因此评价结果确定为Ⅵ级，反映了水体的富营养化程度。将样本在不同指标集下进行分析，可以得出不同粒度下的评价结果，同时也能根据不同粒度下的评价结果，分析出水体富营养化的变化趋势。

（2）Gamma-云方法采用的是层次分析法确定权重，该方法能把复杂的决策思维进行层次化，但对于某些指标，各专家意见不一致时，无法建立完全判断矩阵;改进粗-云方法中云模型参数和超熵的确定存在一定主观性和随机性;模糊可变集法是运用人的基本经验和知识，确定各个指标的权重，具有主观性;单一指标法以各指标的最高等级作为最终评价结果，以偏概全，不能客观反映水体实际情况;神经网络法对隐含层中神经元的个数有较大依赖性，并且神经元的个数都是人工设定的，设定的合理与否会直接影响评价结果的准确性;投影寻踪法中投影目标函数的建立及其优化问题比较复杂。以往的水体富营养化评价方法都存在一定局限性，也不能让用户根据自身需求得到不同粒度下的水体富营养化评价结果。集对多粒度水体富营养化评价方法通过获取属性重要度，分级建立各指标集对关联度，集对关联度的建立相较于投影目标函数的建立简单易行，同时可以处理不确定性问题。样本的评价等级是根据最大正同度所在的等级确定的，若存在正同度相同的情况，则增加负反度进行分析，选择负反度最小的等级作为评价结果;根据属性重要度的大小，建立不同粒度的指标子集进行水体富营养化评价，形成不同粒度的水体富营养化评价结果，综合考虑了所有指标的影响，让用户可以多层次、多角度对评价结果进行分析，其评价结果更为精确、客观。本文提出的多粒度水体富营养化评价方法，在建立集对关联度的时候对所有指标进行综合考虑，不需要考虑主观因素的影响，并且该方法可以根据不同粒度的评价结果分析水体富营养化的变化趋势，为水体的保护提供依据。

3 結 论

集对多粒度水体富营养化评价模型是从评价指标的多粒度多层次出发，将各个指标分级别建立集对关联度，通过考虑最大正同度以及最小负反度，确定评价确定度，再根据用户需求，形成不同的指标子集，综合考量不同粒度下的评价结果，从而得到多粒度的评价结果。根据评价结果将我国12个代表性湖库水体富营养化程度分为4类，其中Ⅲ级的有2个、Ⅳ级的1个、Ⅴ级的4个、Ⅵ级的5个，水体富营养化达到Ⅵ级的湖库急需采取措施来改善水质。该模型运用集对信息粒方法，通过动态选取不同指标集构建评价模型，仅从数据本身进行分析，评价结果以客观存在的数据为依据，消除了主观因素的影响，更有说服力，另外根据用户分析问题时选取的不同粒度，从而构造出不同粒度的分析模型，得到多粒度的评价结果，使得综合决策更加符合客观实际需求。建立的集对关联度，能清晰看出各个级别的关联程度，而且计算方法简捷、直观，适用性更强。

参考文献：

[1] 杨旭，曾祥亮.基于单因子评价法和污染指数法的郑州大学眉湖水质评价[J].江苏科技信息，2014（5）：51-53.

[2] LI Y，ZHANG Z，FEI Y，et al. Improvement of Nemerow Index Method and Its Application[J]. Water Resources Protection， 2009，35（6）： 48-50.

[3] LIU D， HU N， LIU H Y， et al. The Evaluation of the Water Quality of Shenwo Reservoir Based on Fuzzy Comprehensive Evaluation Method[J]. Advances in Industry and Civil Engineering， 2012， 594-597： 2061-2065.

[4] 魏娟.基于模糊综合评价法的赛里木湖水质评价[J].新疆水利，2017（6）：43-47.

[5] 庞博，李玉霞，童玲.基于灰色聚类法和模糊综合法的水质评价[J].环境科学与技术，2011，34（11）：185-188.

[6] 黄斌.人工神经网络在沅江中上游水环境质量评价中的应用研究[D].长沙：湖南大学，2006：13-25.

[7] 姜明岑，王业耀，姚志鹏，等.地表水环境质量综合评价方法研究与应用进展[J].中国环境监测，2016，32（4）：1-6.

[8] 王文圣，张翔，金菊良，等.水文学不确定性分析方法[M].北京：科学出版社，2011：1-7.

[9] 赵克勤.集对分析及其初步应用[J].大自然探索，1994（1）：67-72.

[10] SU M R，YANG Z F， CHEN B. Set Pair Analysis for Urban Ecosystem Health Assessment[J]. Communications in Nonlinear Science and Numerical Simulation，2009，14（4）： 1773-1780.

[11] 赵嶷飞，万俊强.基于集对分析的航空公司安全风险评估研究[J].安全与环境学报，2018，18（5）：1711-1715.

[12] 赵海超，苏怀智，李家田，等.基于多元联系数的水闸运行安全态势综合评判[J].长江科学院院报，2019，36（2）：39-45.

[13] WEI C，DAI X，YE S，et al. Prediction Analysis Model of Integrated Carrying Capacity Using Set Pair Analysis[J]. Ocean & Coastal Management， 2016， 120： 39-48.

[14] 張春英，王立亚，李明霞，等.基于集对信息粒空间的三支决策模型及应用[J].通信学报，2016，37（增刊1）：15-24.

[15] 舒金华.我国湖泊富营养化程度评价方法的探讨[J].环境污染与防治，1990，12（5）：2-7.

[16] 付文艺.基于熵权-正态云模型的地下水水质综合评价[J].人民黄河，2016，38（5）：68-71.

[17] 刚什婷，贾涛，邓英尔，等.基于熵权法的集对分析模型在蛤蟆通流域地下水水质评价中的应用[J].长江科学院院报，2018，35（9）：23-27.

[18] 王靖，张金锁.综合评价中确定权重向量的几种方法比较[J].河北工业大学学报，2001，30（2）：52-57.

[19] 刘登峰，王栋，丁昊，等.一种Gamma-云的富营养化评价方法及其应用[J].水文，2014，34（5）：45-50.

[20] 卢媛，王栋，刘登峰，等.基于改进的粗糙集-云模型的水质评价方法[J].南京大学学报（自然科学），2017，53（5）：879-886.

[21] 陈守煜，郭瑜.水质综合评价的模糊可变集合方法[J].水资源保护，2005，21（6）：19-22.

[22] 崔东文.几种神经网络模型在湖库富营养化程度评价中的应用[J].水资源保护，2012，28（6）：12-18.

[23] 王贵作，任立良，王斌，等.基于投影寻踪的湖泊富营养化程度评价模型[J].水资源保护，2009，25（5）：14-18.

【责任编辑 吕艳梅】