数学活动经验：在『做』与『思』中自然生长

[摘要] 数学活动经验的积累需要教师精心设计教学活动，创设恰当的活动情景，激发学生已有经验;要让学生经历丰富的活动过程，并在学习活动的基础上对数学经验进行反思内化，促使经验生长。

[关键词] 数学活动;经验;过程;反思

一、数学活动经验的内涵特征

数学活动经验是指学生在经历数学活动过程中获得的感受、体验、领悟以及由此获得的数学知识、技能、情感等，具备如下特征：

1.生长性。学生数学活动经验“有助于学生形成完整的数学认知结构，并对后续学习和发展产生积极的影响”。它对学生获得良好的数学教育、提升数学素养有着深远的意义。

2.过程性。积累数学活动经验必须要使学生不断地经历、体验各种数学活动。数学活动经验的积累就是在这些“做”与“思”的过程中不断发展。

二、促进数学活动经验生长的基本策略

（一）创设恰当的活动情景，激发已有经验

“数学来源于现实，存在于现实，并且应用于现实。”小学阶段的学生，正处于从形象思维过渡到抽象思维的阶段，恰当有效的教学情境，有助于激发起学生已有的生活经验和相关的数学活动经验，为新知的学习做好思维的铺垫和伏笔。例如，在学习平面图形的面积时，研究“同样长度的线段围成什么图形面积最大”这一问题时，引导学生手牵手围成一圈，每个人尽量地向外拉，此时围成的面积最大，而这个时候围成的图形是圆形。

通过激活学生的生活经验，使得这个问题得到巧妙解答。以这样鲜活有趣的形式，既抓住了学生的兴趣点，又唤醒了学生对“面积最大”的生活经验，为接下来的系统探究奠定基础。虽然这样的经验只是生活化的、浅显的、感性的，但依然是新知学习不可或缺的部分。

（二）经历丰富的活动过程，积累活动经验

“基本活动经验是学生亲自或者间接经历活动过程而获得的经验”，在课堂教学的过程中，教师应该尽可能地让学生主动参与到活動探究的过程中。

1.在具体操作中积累直接经验

美国教育家戴尔曾经提出经验之塔理论，在经验之塔的底部几层分别是“有目的的直接经验”“设计实验”和“参与活动”。该理论启示我们，学习最好从直接参与的动作性经验开始，以获得直接经验。例如，在“认识千米”的教学过程中，课前笔者带领学生到操场上走完1千米。在课堂上，学生结合走路的过程，从以下方面予以反馈。

师：我们走完1千米用了多久？大约有多少步？

生1：大约13分钟，2 500步。

师：走完后大家有什么感觉？

生2：有点累，都流汗了。

生3：感觉比我们之前学习的长度米、分米和厘米要大得多。

在这样的活动过程中，学生不仅有长度上的感知，更有时间、身体的感觉等一系列的感受，从而在认知结构中更加立体地建立起对“千米”这一概念的直接经验。

当然，学生形成正确而清晰的直观体验依赖操作材料、活动环节、问题设计等诸多方面，在每一个环节教师都要全面预设，避免学生因生活经验不足而形成错误的活动经验。

2.在直观想象中积累间接经验

直接经验的获取对学生核心素养的提升有着不可替代的作用，但是学生学习不可能每一个场景都去亲身体验。学校学习主要是文化继承的过程，我们能够去体验和经历的事情只是极少一部分，而更多的时候需要充分地发挥大脑想象的功能，寻求间接经验的帮助，弥补直接经验的不足。因此，应充分整合各种教育教学技术和手段，让学生在直观想象、模仿中获得身临其境的经历和体验。例如，在教学“认识吨”的过程中，因为条件限制，学生不可能亲自体验到1吨甚至10吨的重量，只能充分发挥自己的想象。

师：一袋10千克的大米，要有100袋这样的大米才是1吨，想象一下100袋有多少，如果摆放在我们教室里，应该会占用多大空间？

生1：会占据大概这么大的地方。（学生用身体比划，其他学生惊叹）

师：三年级的小朋友体重大约20千克，那多少个小朋友加起来重量就会有1吨呢？

生2：50个。

师：是啊，相当于我们整个班级所有的学生加起来重量大约1吨。

生3：哇，原来1吨这么重啊。

在这个过程中，教师充分运用了学生想象，让学生体验到1吨的重量。虽然没有直接、亲身的体验，但是这样的活动依然使学生获得了充分的间接经验，满足了学生的心理需求，获得了积极的情感体验，充实了数学活动经验的具体内容。

（三）反思经历的数学活动，内化活动经验

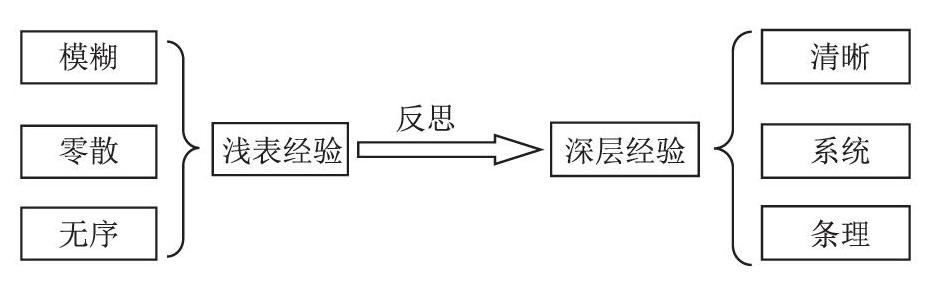
在经历了丰富的数学活动之后，学生获取了一定的经验，但此时学生所获取的还是模糊的、零散的、无序的浅表化经验。这样的经验如果不经过进一步的加工处理，很容易丢失遗忘，对后续知识的学习作用微乎其微，甚至还会出现前摄知识干扰的现象。这时，自我的反思就显得尤为重要，只有经过反思，学生才会将这些经验的“碎片”条理化、系统化和清晰化，形成深层性的活动经验。因此，教师在课堂教学过程中，应该引导学生对数学活动过程中所获取的经验进行回顾和总结，反思自己是怎样发现问题、怎样解决问题、用了哪些思考的策略和方法。经过这样的升华和内化，学生的活动经验才会是有联系的，才是不断生长的。

例如，在教学“轴对称图形”一课时，研究平行四边形、长方形、菱形和正方形分别有几条对称轴，笔者引导学生作了以下反思。

师：我们刚刚画出了每一个图形的所有的对称轴，回忆一下你是怎样找到每一个图形的对称轴的？

生1：我是通过折一折的方法。

师：还有吗？

生2：我就是自己在脑子里想象的。

师：你的空间想象能力很好。那么，同样都有两组对边分别平行，为什么平行四边形不是轴对称图形呢？

生3：因为无论沿哪一条线对折，都不能完全重合。

师：那为什么长方形和菱形只有两条对称轴，而正方形却有四条对称轴呢？

生4：因为正方形是特殊长方形也是特殊的菱形，所以菱形和长方形的对称轴正方形都有，所以正方形有四条对称轴。

在这个教学环节中，教师通过两次有层次的比较，引导学生回忆探索图形对称性的方法，进一步内化了学生已有的活动经验，使学生对图形对称性的理解更加清晰和系统。在学生积累了一定的数学活动经验之后，教师通过恰当的活动来引导学生对原本的经验进行有效反思，这样不仅可以把经验的积极作用有效地凸显出来，同时也很好地规避活动经验的不良因素，使积累起来的数学活动经验能更好地为学生所用。

胡峰光   江苏省常州市武进区人民路小学。