中法海洋卫星散射计噪声分析及自适应估计

云日升，高畅畅，2，王冰花，于淼淼，3

(1.中国科学院国家空间科学中心，北京 100190；2.中国科学院大学 计算机科学与技术学院，北京 100049；3.中国科学院大学 电子电气与通信工程学院，北京 100049)

0 引言

中法海洋卫星(China-France oceanography satellite，CFOSAT)是中法两国合作研制的首颗卫星，中方负责提供卫星平台、海风观测载荷以及发射测控，法方负责提供海浪观测载荷，卫星数据双方共享。2018年10月29日8时43分，中法海洋卫星在酒泉卫星发射中心用长征二号丙运载火箭成功发射，可获得全球海面风场、海浪谱以及有效波高等海洋动力参数，有助于更好地认识和掌握海洋动力过程及变化规律，为海洋预报提供海浪谱、海面风场等多参量的初始场信息，改进海况预报及同化模型，提高对巨浪、热带风暴、风暴潮等灾害性海况预报的精度与时效[1]。中法海洋卫星对海浪、海面风场进行同步监测，可为海洋科学研究、全球气候变化提供实测数据并且积累长时间序列历史数据。图1是CFOSAT散射计观测几何示意图。散射计天线通过旋转机构安装在卫星下方。

图1 CFOSAT散射计观测几何示意图

中国科学院国家空间科学中心承担研制的微波散射计是国际上首个扇形波束旋转扫描散射计(rotating fan-beam scatterometer，RFSCAT)[2]，散射计的工作频率为13.256 GHz(Ku波段)，轨道高度为520 km，测绘带刈幅为1 000 km，地球表面日覆盖率约为90%。系统平行配置两个分别对应于垂直和水平极化的缝隙波导阵列天线实现扇形波束圆锥扫描，获得观测目标的多个方位角和俯仰角组合的后向散射系数[3]，可以有效改善海面风场的反演精度。

CFOSAT散射计的风速测量误差小于1.5 m·s-1，风向测量误差小于15°，处于世界领先水平[4]。图2是CFOSAT散射计在2020年9月6日观测的全球海面后向散射系数分布图。

图2 CFOSAT散射计单日全球覆盖

1 噪声估计与后向散射系数计算

图3是CFOSAT散射计微波前端信号通道示意图。散射计按照收发时序通过收发开关切换实现水平极化和垂直极化射频信号发射和回波接收。将发射信号耦合到接收端得到内定标信号，用于比例定标以消除发射功率和接收机增益的波动。CFOSAT散射计按工作时序同时获取内部噪声信号和外部噪声信号。内部噪声信号对系统热噪声源进行采样，外部噪声信号来自天线端被动接收的观测区域噪声能量。根据雷达方程，获取观测区域的σ首先需要由回波能量中去除噪声能量得到观测区域实际散射信号的能量[5]。

图3 CFOSAT散射计微波前端信号通道

CFOSAT散射计扇形波束俯仰向观测范围为26°～46°，在俯仰向近端和远端约有300 kHz的Doppler频率差，同时Doppler频率与扫描方位向和星下观测点纬度有关，系统采用了发射信号中心频率预偏移实现Doppler频率预补偿[6]。回波信号在星上首先进行全去斜处理，经过I/Q解调和数字下变频之后，对基带信号进行FFT变换到频域[7]。对扇形波束脉冲频域信号按照查找表进行条带能量累加，获得40个条带的回波能量[8]。查找表根据回波频率和地面条带尺度对应关系计算得到。噪声信号未进行FFT，直接累加得到当前脉冲对应的总的噪声能量，实际处理中需要将总的噪声能量根据条带能量对应关系将噪声能量分配到各个条带中。

由回波能量中分离出对观测信号能量的处理，如式(1)所示。

Es，i=Er，i-CiEn，i，i=1，2，…，Nslice

(1)

式中：Er，i为条带回波能量；Es，i为条带信号能量；Ci为噪声估计校正因子；Nslice为条带数，对CFOSAT散射计而言，取值为40。由Parseval定理，条带噪声能量如式(2)所示。

(2)

式中：En为当前脉冲总噪声能量；Nr为FFT后脉冲回波点数；Nn为噪声采样点数；Ni为由星上查找表确定的第i个条带能量积累点数。

由式(1)获得了条带观测目标散射信号能量之后，条带后向散射系数由雷达方程计算得到，如式(3)所示。

(3)

式中：A为雷达方程中的常数项因子，定标因子如式(4)所示，积分因子如式(5)所示。

(4)

(5)

式中：PtGr为发射功率接收增益积；Lsys为系统损耗；gj为脉冲照射区域内积分面元天线方向图；ΔAj为面元积分面积；T为取样间隔；N为FFT长度；ks和ke为FFT抽头系数的起始点和结束点[9]。

在噪声估计过程中，由于回波通道与噪声通道系统滤波器幅频特性可能存在不一致性，通常由式(2)计算得到的条带噪声能量存在误差，需要进行校正。因此，对噪声能量进行校正，获得噪声估计校正因子，最终实现条带噪声的准确估计。

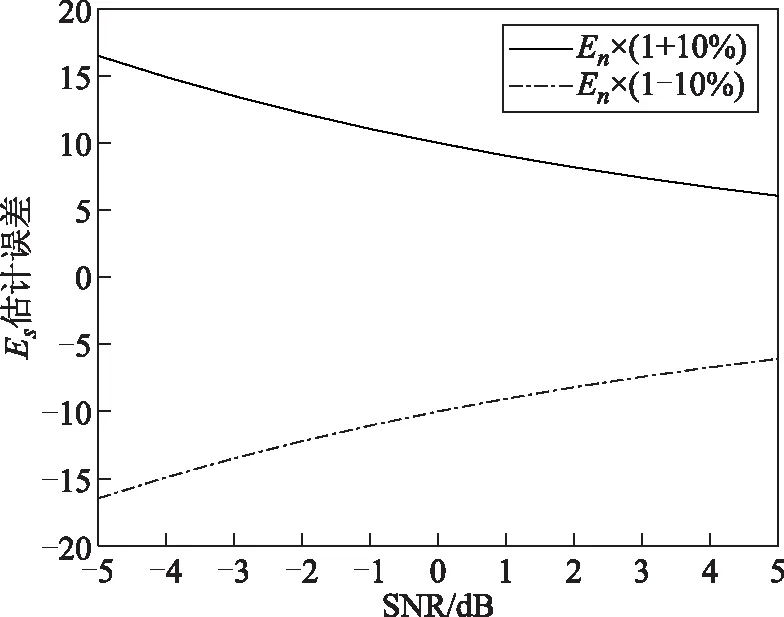
图4 噪声能量估计偏差对信号能量的影响

图4为噪声能量估计偏差对信号能量的影响。由图4可知，在SNR比较高的条件下对信号能量估计的影响比较小；在SNR比较低的条件下对信号能量估计的影响比较大。如SNR为 5 dB时，噪声能量估计值En偏差10%，引起Es约6%的误差；当SNR 为 -5 dB，噪声能量估计值En偏差10%，引起Es约17%的误差。对于CFOSAT散射计，在偏离扇形波束中心远端或在较低风速情况下，其SNR通常小于0 dB。因此，提高CFOSAT散射计噪声能量的估计精度能够改善风场反演的性能。

2 CFOSAT散射计信号稳定性分析

通常，在接收信号比较稳定的情况下，根据风场反演结果闭环迭代获得噪声估计校正因子Ci的经验值。当接收信号存在不稳定波动的情况下，通常难以获得一致的噪声校正因子，自适应地获取噪声校正因子成为CFOSAT散射计预处理的难点之一。

图5为CFOSAT散射计不同时间段内部噪声信号和定标信号随时间的稳定性情况(每天抽取4轨数据)。图5(a)、图5(b)为2019年8月16—31日内部噪声和定标信号数据，图5(c)、图5(d)为2020年8月16—31日内部噪声和定标信号数据。数据取值均为科学数据包中表示能量的采样值。由图5可知，CFOSAT散射计信号稳定性在不同时间段存在不一致。经对散射计长期观测数据分析，2019年数据整体稳定性较好，内部噪声信号的整体稳定性在0.2 dB以内；2020年某些时间段数据波动较大，内部噪声某些时间段信号稳定性大于0.5 dB。信号稳定性差异可能与轨道变化引起的太阳辐照、设备状态或器件温度特性有关，需要进一步分析。分析表明，2020年某些时间段的数据由于数据稳定性较差，使用固定的经验性噪声校正因子会带来一定的风场反演误差，需要根据数据变化实现噪声校正因子的自适应调整。

图6给出了2020年8月16—31日的温度遥测数据。比较图6与图5(c)、图5(d)可知，数据稳定性与温度遥测在趋势上有一定的相关性，但由于温度遥测数据点数较少(小于100点测温值/天)，定量获取温度与数据稳定性之间的关系比较困难，因此，本文通过建立实际数据与噪声校正因子的自适应模型来实现噪声校正因子随数据波动的自适应调整。由于内部噪声可以反映出星上器件随卫星舱内温度变化的波动，外部噪声易受地表亮温变化的影响，因此，本文主要通过内部噪声和定标信号与噪声校正因子之间的相关性来构建噪声校正因子的自适应调整模型，之后在自适应噪声模型的基础上，结合外部噪声信号实现噪声定标和观测目标后向散射系数的计算。

图5 不同时间段信号稳定度比较

图6 温度遥测(2020年8月16—31日)

3 CFOSAT散射计噪声校正因子自适应模型与算法

当目标观测信号的SNR小于0 dB，回波能量和噪声能量数值上比较接近，就会出现后向散射系数取负值的情况。为了获得噪声校正因子的估计，假设风速小于1 m·s-1时回波能量近似等于噪声能量，此时负σ占比约50%。考虑到数据波动特点和处理复杂度，将噪声因子自适应调整时间间隔设定为单轨时间(约90分钟)。对ECMWF风场数据，在考察时间段内每个脉冲的观测时间和经纬度上进行时空插值匹配，按单轨搜索在1 m·s-1风速以下，负σ占比50%时的噪声校正因子作为初始估计值。实验表明，这样假设和处理能够获得噪声因子变化趋势的合理估计，可以给出单轨数据较为准确的噪声校正因子估计值。对于扇形波束散射计，实际处理中需要对多个入射角估计值进行加权平均，并根据风场反演结果进行迭代计算以获得单轨噪声能量估计校正因子的准确值。

图7为噪声能量估计校正因子与单轨数据内部噪声均值随时间变化的相关性。图中选择2020年8月16 —31日242轨数据，分别由ECWMF风场1 m·s-1风速以下，负σ占比50%匹配搜索得到每一轨的噪声能量估计校正因子，同时计算该轨数据内部噪声的均值。由图7可知，噪声校正因子与内部噪声均值变化趋势一致，有较好的相关性，且V极化相关性较H极化更好。图8为噪声能量估计校正因子与单轨数据定标信号能量均值随时间变化的相关性，与单轨内部噪声能量均值情况相类似，噪声校正因子与单轨定标信号能量均值有较好的一致性。图7和图8表明，可由内部噪声能量均值或定标信号能量均值与噪声能量校正因子之间的相关性建立噪声校正因子分时间段的实时调整模型。

图7 噪声因子与内部噪声均值的相关性

图8 噪声因子与定标信号均值的相关性

由于卫星进出地影会引起散射计温度的变化，参考卫星轨道进出地影前后时间段，随机选取2020年2、8、9月份的散射计数据，分析单轨内部噪声和定标信号的均值之间的线性关系(其中2月121轨，8月242轨，9月151轨)。图9为上述三个时间段单轨内部噪声能量均值与定标信号能量均值线性相关度比较。由图9可知，不同时间段内部噪声能量均值与定标信号能量均值之间不具有一致的线性相关性。

这一结果表明，若用内部噪声能量均值或者定标信号能量均值作为参考量，建立噪声校正因子的单参量模型，则这种单参量模型不具有全局一致性。即依据某一时间段内数据建立的模型不适用于其他时间段噪声能量的估计。以下考虑单轨定标信号能量均值和内部噪声能量均值建立二元噪声校正因子估计模型，实现噪声校正因子的全局一致性自适应估计。

采用加权最小二乘法多项式曲面拟合的方法[10]，选取单轨定标信号能量均值作为x变量，单轨噪声能量均值作为y变量，噪声能量估计校正因子作为z变量，则问题可简化为：给定一组样本点(xk，yk，zk)，k=1，2，…，N，利用式(6)对样本点进行拟合。

(6)

式(6)可转化为式(7)。

f(X，Y)=XTAY

(7)

求出系数矩阵A即可得到拟合的曲面。其中：

(8)

利用加权最小二乘法构造出关于aij的多元函数，如式(9)所示。

(9)

式中：ωk为加权系数。根据式(10)求出式(9)取最小值的系数矩阵A即可。

(10)

在训练集上不同的拟合方式结果如表1所示。polypq表示x的最高次数是p，y的最高次数是q。SSE代表残差平方和，R-sq表示确定系数，R-sq(Adj)表示校正确定系数。将表1中八种拟合模型分别用于自适应估计，发现两次以上的拟合模型会出现过拟合现象，采用poly21模型拟合精度最高。模型的数学表达如式(11)所示。

kfit=p1+p2x+p3y+p4xy+p5y2

(11)

式中：pi(1≤i≤5)为poly21模型二元曲面拟合多项式系数。

表1 九种拟合方式的效果

利用2020年2月(121轨)、4月(81轨)、5月(92轨)、6月(117轨)、8月(242轨)和9月(151轨)的L1A数据建立的数学模型拟合曲面如图10所示。利用多项式拟合得到的模型计算单轨减噪声因子拟合值kfit。拟合值kfit与搜索出的最优值kopt基本一致，两者之间的比较如图11所示。从图11中可看出，双参量自适应模型给出的减噪声因子kfit相当于对最优值kopt做低通滤波的结果。该模型具有较好的数据适应性，能够满足风场反演的要求。

图10 二元多项式噪声因子曲面拟合

图11 噪声校正因子拟合值与最优值比较

图12是未采用自适应模型的双极化风场反演风速风向偏差图，图13是采用自适应模型的双极化风场反演风速风向偏差图(2020年8月16—31日)。由图12、图13可知，采用自适应噪声估计处理之后，风场反演结果有了明显的改善，特别是与ECWMF风场相比较，在小于20 m·s-1风速的条件下，平均风速反演偏差由0.25 m·s-1下降到0.1 m·s-1以内。

图12 未采用自适应噪声估计的风场反演结果

图13 采用自适应噪声估计的风场反演结果

4 结束语

中法海洋卫星是中法两国合作研制的首颗卫星，通过对海浪、海面风场同步监测，可获得全球海面风场、海浪谱以及有效波高等海洋动力参数。初步性能验证表明，中法海洋卫星散射计风速精度优于1.5 m·s-1，风向精度优于15°，其在风场测量上的性能达到国际先进水平。噪声能量估计是CFOSAT散射计数据预处理中的重要问题之一，准确的噪声能量估计和校正决定了反演得到的空间对地观测后向散射系数的精度。

本文简要介绍了CFOSAT散射计的信号通道及星上回波和噪声信号的处理过程，描述了噪声能量估计和后向散射系数的计算方法。噪声能量的准确估计决定了后向散射系数计算的精度，进而影响风场反演的性能。特别是在低信噪比的情况下，噪声能量估计误差对后向散射系数精度影响较大。通过对不同时间段散射计数据稳定性的分析表明，需要针对不同时间段的数据特点，自适应地调整噪声能量估计的噪声校正因子。本文分析了内部噪声能量均值、定标信号能量均值与噪声校正因子之间的相关性和不同时间段内部噪声能量均值同定标信号能量均值的线性相关度之后，基于最小二乘原理，采用二元多项式曲面拟合方法得到了内部噪声能量均值和定标信号能量均值与噪声校正因子之间的数学模型；利用该模型自适应调节噪声能量估计校正因子，改善了后向散射系数计算精度，获得了稳定、准确的风场反演性能。