波轮洗衣机悬挂系统动力学建模及动力学特性研究

张强 杨洪永 熊瑞 周鑫林

ZHANG Qiang YANG Hongyong XIONG Rui ZHOU Xinlin

珠海格力电器股份有限公司 广东珠海 519070

Gree Electric Appliances, Inc. of Zhuhai Zhuhai 519070

1 引言

洗衣机已经成为不可或缺的家用电器之一。按洗涤方式的不同，洗衣机可分为波轮式、滚筒式和搅拌式等。国内市场以波轮洗衣机和滚筒洗衣机为主，且滚筒洗衣机所占比重越来越高，但波轮洗衣机因为价格低廉、洗净度高、洗涤容量大等优势，仍然占有相当的市场份额。

随着对生活品质需求的不断提升，用户对家用电器的要求也越来越高，特别是振动水平，已经成为衡量洗衣机性能的关键指标之一。波轮洗衣机源起日本，我国波轮洗衣机起步于技术引进或产品模仿，而且国内洗衣机厂商研发重点集中在产品本身，对波轮洗衣机振动机理缺乏深入研究。对洗衣机的减振，仍以试错式的样机验证为主，产品在设计初期缺乏低振动设计的理论指导，导致振动问题较多，且严重影响产品开发进度。

目前有关波轮洗衣机振动特性的文献较多，钱静[1]，陈海卫[2]等对波轮洗衣机悬挂系统的动力学特性进行了细致研究，但所建立的振动模型都较为复杂，不适于洗衣机结构设计工程师直接使用。本文将波轮洗衣机悬挂系统的运动简化为平面二自由度系统的运动，并建立了其二自由度运动微分方程，然后对此二自由度系统的动力学特性进行了研究，探讨了平衡环和吊杆安装位置对悬挂系统振动的影响，提供了一种研究波轮洗衣机悬挂系统振动的工程方法。

2 悬挂系统动力学建模

2.1 模型简化

波轮洗衣机桶部件通过四根吊杆悬挂于箱体四角，如图1a)所示，吊杆上端（吊杆座）与箱体角板连接，下端（上托）与桶部件连接，上下连接点均可视为球铰，如图1b)所示，故吊杆的金属杆只承受轴向载荷，为二力杆模型，吊杆阻尼筒（即上托）内包含弹簧和阻尼元件，分别用于缓冲桶部件的振动冲击和抑制桶部件的共振幅值。

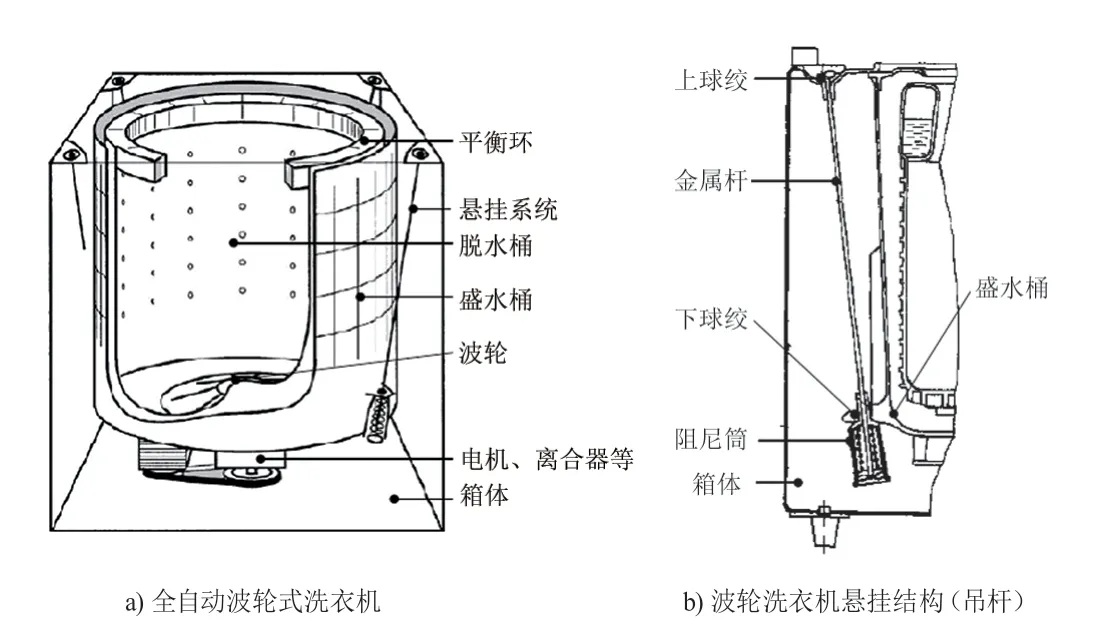
图1 全自动波轮洗衣机结构图[3]

波轮洗衣机于脱水转速稳定运行时，桶部件径向振幅可视为沿圆周方向处处相等，故可将其悬挂系统运动简化为平面运动，在简化平面内有两个运动分量，分别是桶部件的平动（表现为吊杆类似于单摆的摆动）和转动，由此可将波轮洗衣机悬挂系统的运动模型简化为平面二自由度模型。

将吊杆与桶部件的连接方式进行简化，将四根吊杆简化为一根，吊杆与桶部件的铰接点简化至桶轴线与弹簧支点连线的交线处，如图2所示。图3为波轮洗衣机悬挂系统的平面二自由度模型图，桶部件的平动表现为吊杆的转动，记为θ1，桶部件的转动记为θ2，本文将针对简化的模型进行数学建模和求解。

根据重心位置不同，如图4所示，可以将悬挂系统二自由度模型分为三种：a)桶部件质心在弹簧支点上侧；b)桶部件质心与弹簧支点同高度；c)桶部件质心在弹簧支点下侧，本文主要讨论第三种情况，即空桶偏心工况。

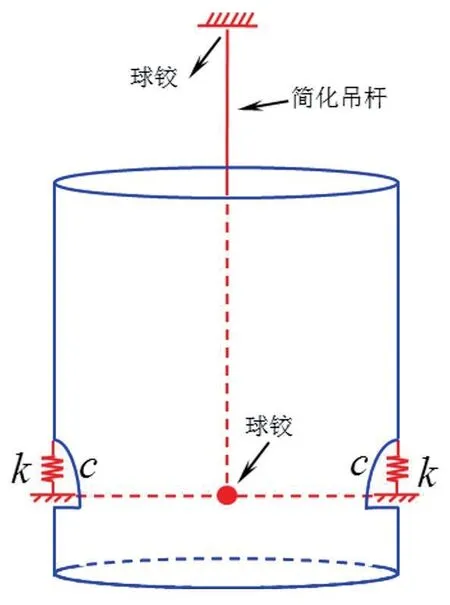
图2 波轮洗衣机悬挂系统动力学简化模型

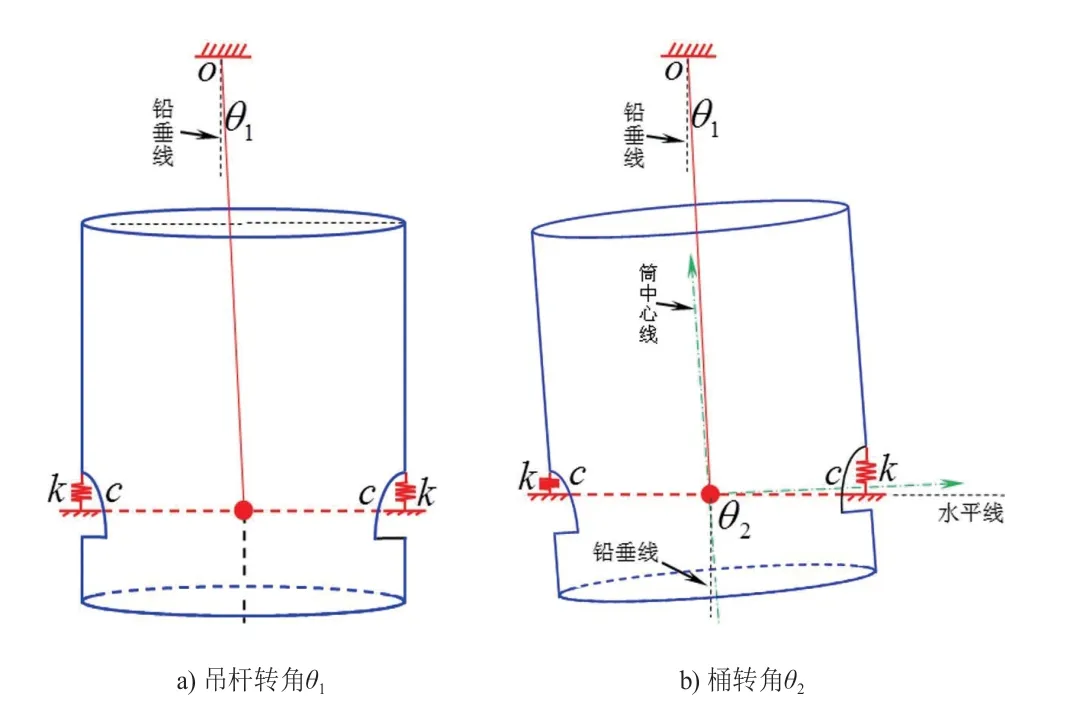
图3 波轮洗衣机悬挂系统平面二自由度模型

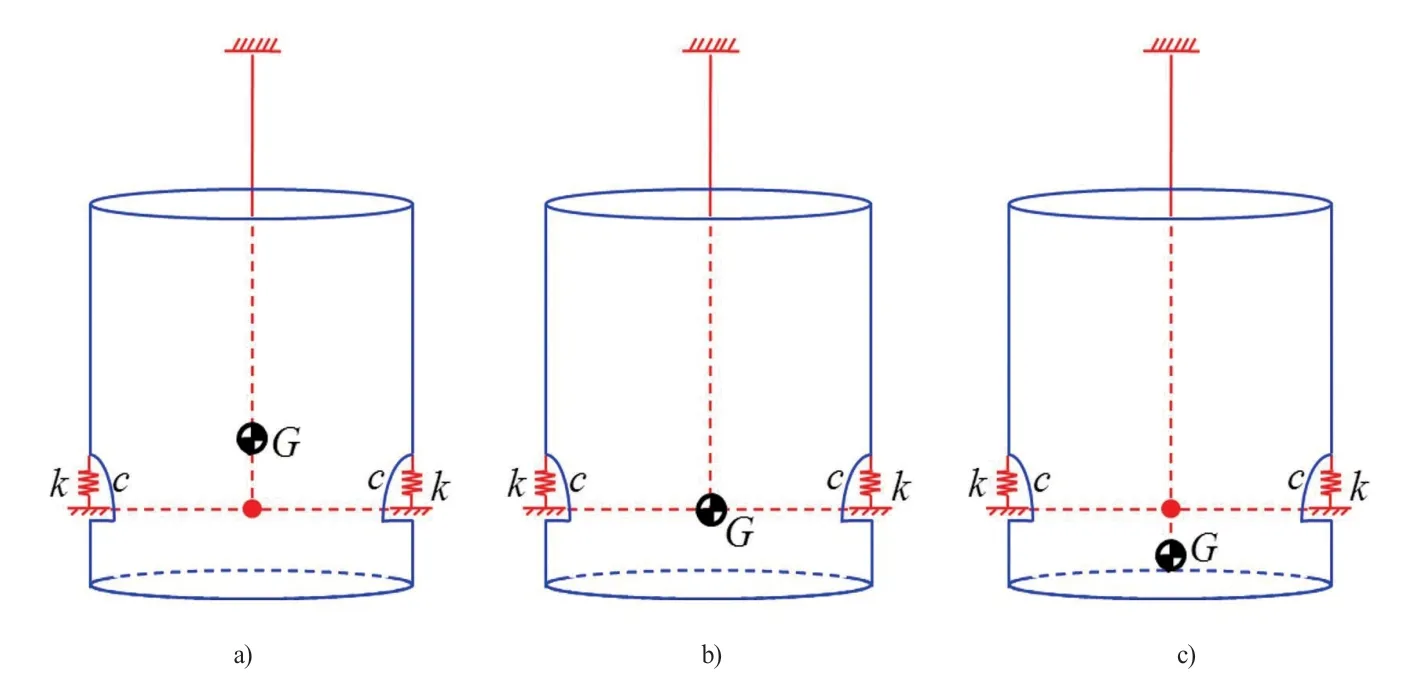
图4 桶部件质心位置的三种情况

2.2 动力学建模

2.2.1 基本假设

波轮洗衣机悬挂系统平面二自由度模型的初始状态如图5a)所示，本文动力学建模有以下两点基本假设：

（1）仅分析悬挂系统的稳态振动，因阻尼对稳态振动影响较小，故动力学建模中忽略吊杆阻尼c，仅考虑吊杆刚度k；

（2）内桶顶端安装有液体平衡环（见图1），液体平衡环中的液体依据自动定心原理向偏心负载相对一侧移动，理论上在桶部件转速远大于悬挂系统共振转速时，平衡环液体的平衡质量与偏心负载的质量相位差接近180°，本分析假定达到洗衣机最高脱水转速时二者相位差等于180°，即图5a)中偏心质量m1和液体平衡环中液体的抗偏心质量m2的旋转离心力方向相反；另外平衡环液体的偏移量与悬挂系统振动幅值两者之间相互影响，本分析不考虑二者之间的双向耦合问题，假定平衡环中的液体集中于一处，产生的平衡力为m2rω2，其中r为旋转半径。

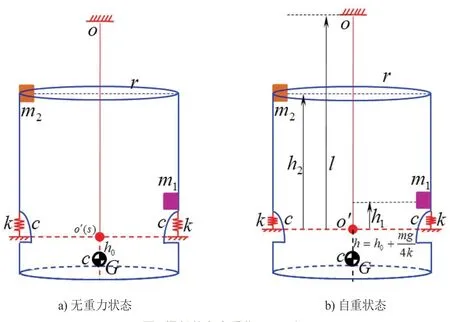
图5 桶部件在自重作用下下沉

2.2.2 运动方程（Equation of Motion）

在简化模型中，吊杆与箱体的铰接点标记为O，将吊杆与弹簧支点连线的交点定义为吊杆与桶部件的铰接点，并标记为O’。图5a)中初始状态在桶部件上与O’点重合位置标记S点，S点为桶部件随体运动点，桶部件在自重作用下下沉，S点下移，与O’点脱离，达到图5b)中的自重状态，O’S长度，即弹簧压缩量，为mg/4k，其中m为桶部件总质量，k为单根弹簧的刚度，四根弹簧并联刚度为4k。

以图5b)自重状态为基准，标记桶部件质心C与O’点高度差、偏心质量m1与O’点高度差、平衡环抗偏心质量m2与O’点高度差分别为h，h1，h2，吊杆长度为l。在图5b)基准状态上，桶部件发生平动和转动运动后各参量的状态变化见图6和图7。

根据达郎贝尔原理，建立针对O点和O’点的力矩动平衡方程，即获得图7所示平面二自由度模型的运动微分方程：

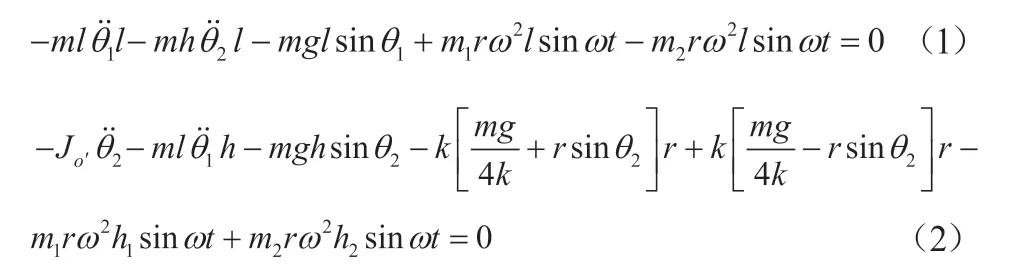
式（2）中，Jo'为桶部件绕O’点的转动惯量，将式（1）、（2）整理为：

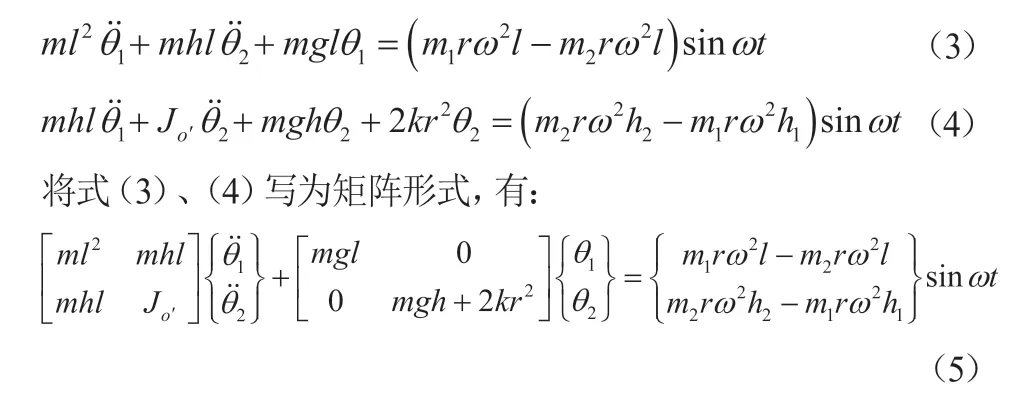
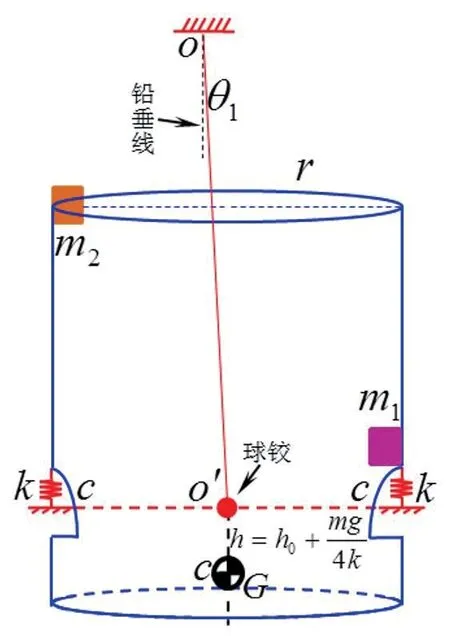
图6 桶部件平动

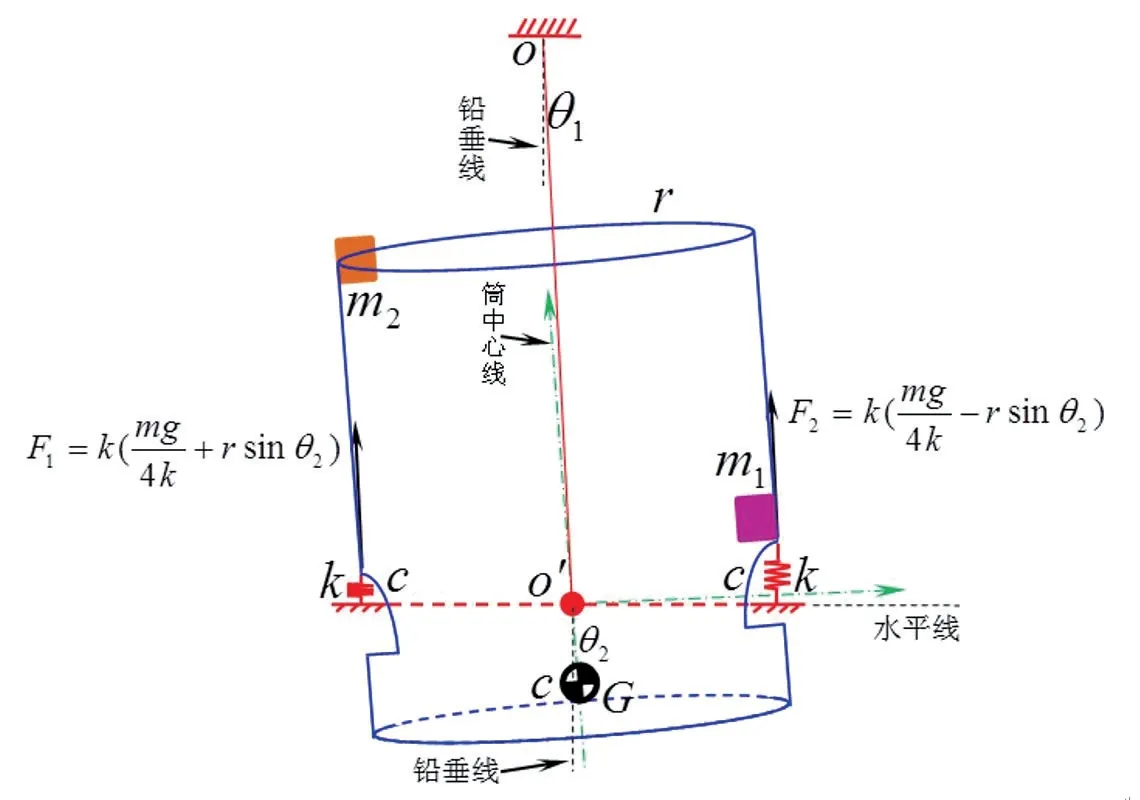
图7 桶部件平动+转动

式（5）即为波轮洗衣机悬挂系统平面二自由度模型的运动微分方程。

使用拉格朗日方法建立该平面二自由度模型的运动方程，广义坐标定义为吊杆绕O点的转角θ1和桶部件绕O’点的转角θ2：

系统动能为：

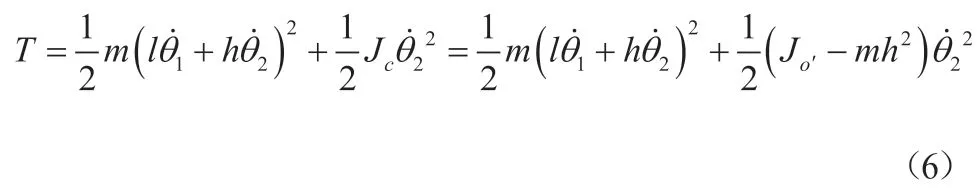
系统势能为：

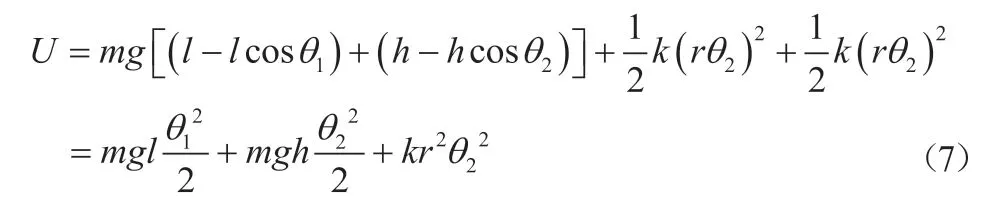
广义坐标θ1和θ2对应的广义力分别为：

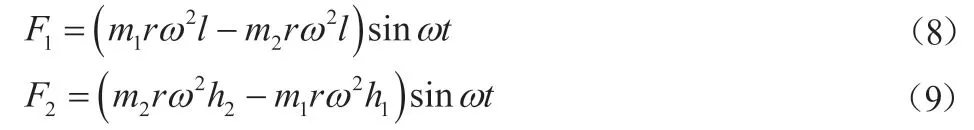
将式（6）、（7）、（8）、（9）代入拉格朗日方程：

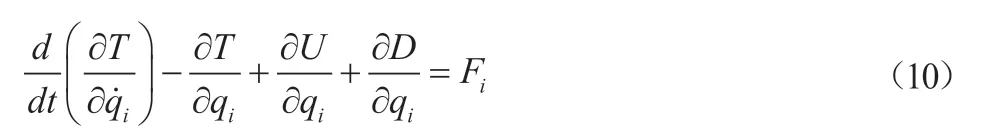
得到系统的运动方程：

将式（11）、（12）写为矩阵形式：

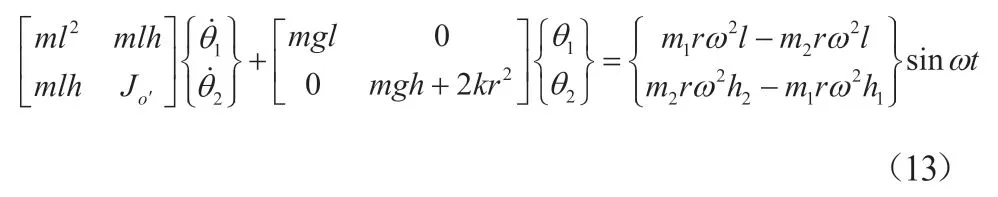
式（5）与式（13）一致，即使用达郎贝尔原理和拉格朗日方法建立的运动方程一致，进一步佐证了所建运动方程的正确性。

2.2.3 模型求解

对式（5）所示运动方程进行求解，并根据求解结果对波轮洗衣机悬挂系统动力学特性进行研究，设定：

将式（14）、（15）代入式（5），式（5）可写为：

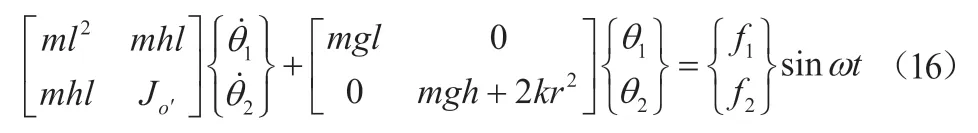
因为是无阻尼系统，假设式（16）的解为：

将式（17）代入式（16）得：

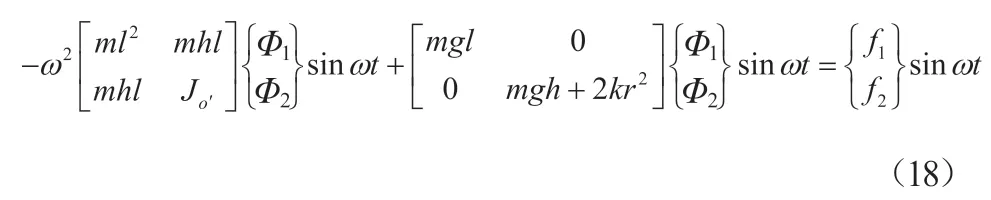
进一步写为：

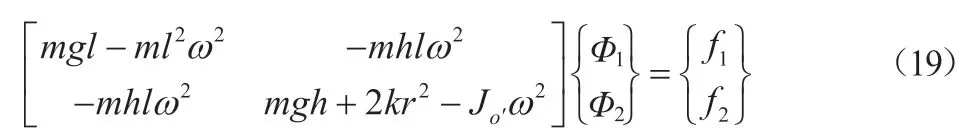
设定：

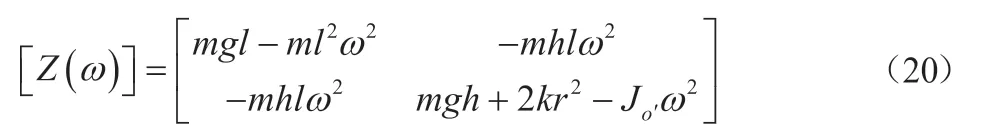
将式（20）代入式（19）得：

式（21）的解为：

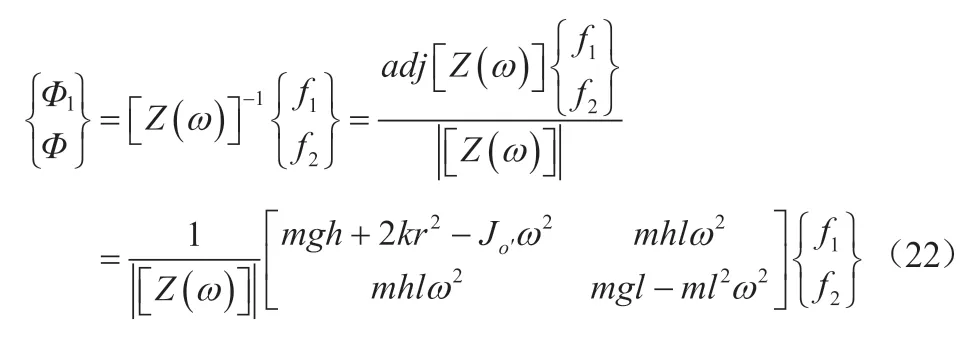
针对式（21），满足如下关系的ω值，则为运动方程的特征值：

运动方程的特征值即为运动系统的固有频率，因为所建模型为二自由度系统，存在两阶固有频率，将其分别标记为ω1和ω2，则存在如下关系：

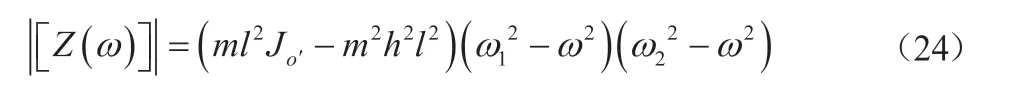
运动方程的最终解为：

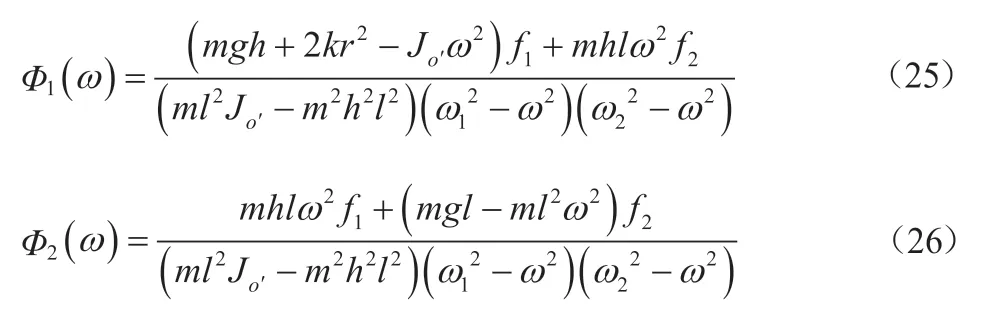
桶部件顶端的合位移为：

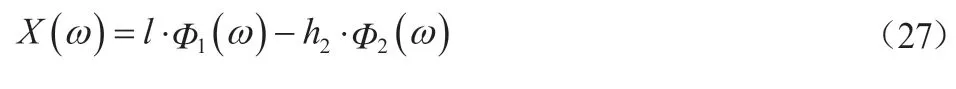
3 动力学特性研究

假设某波轮洗衣机悬挂系统各参数如下：m=20 kg；m1=0.5 kg；m2=0 kg（暂不考虑平衡环平衡力）；Jo'=1 kg·m2；l=0.45 m；r=0.25 m；h=0.05 m；h1=0.06 m；h2=0.3 m；k=2500 N/m。基于此波轮洗衣机系统进行波轮洗衣机悬挂系统的动力学特性分析。

3.1 振型分析

使用设定的悬挂系统各参数，求解式（23），可得运动方程的特征值，即系统的共振圆频率：

按照单摆固有频率公式求解波轮悬挂系统第一阶摆动模态的固有圆频率，如下：

与所建平面二自由度模型解出的第一阶固有圆频率相当，进一步证明了波轮洗衣机悬挂系统第一阶模态的振型等同于单摆的振动。其第二阶模态的振型是与质量、弹簧相关的弹性跳动模态，其大小由悬挂系统质量和弹簧刚度决定。

3.2 平衡环对系统振动的影响

使用设定的悬挂系统各参数，根据式（25）、（26）、（27）绘制Φ1(ω)、Φ2(ω)、X(ω)的幅频曲线，分别如图8、图9、图10所示。

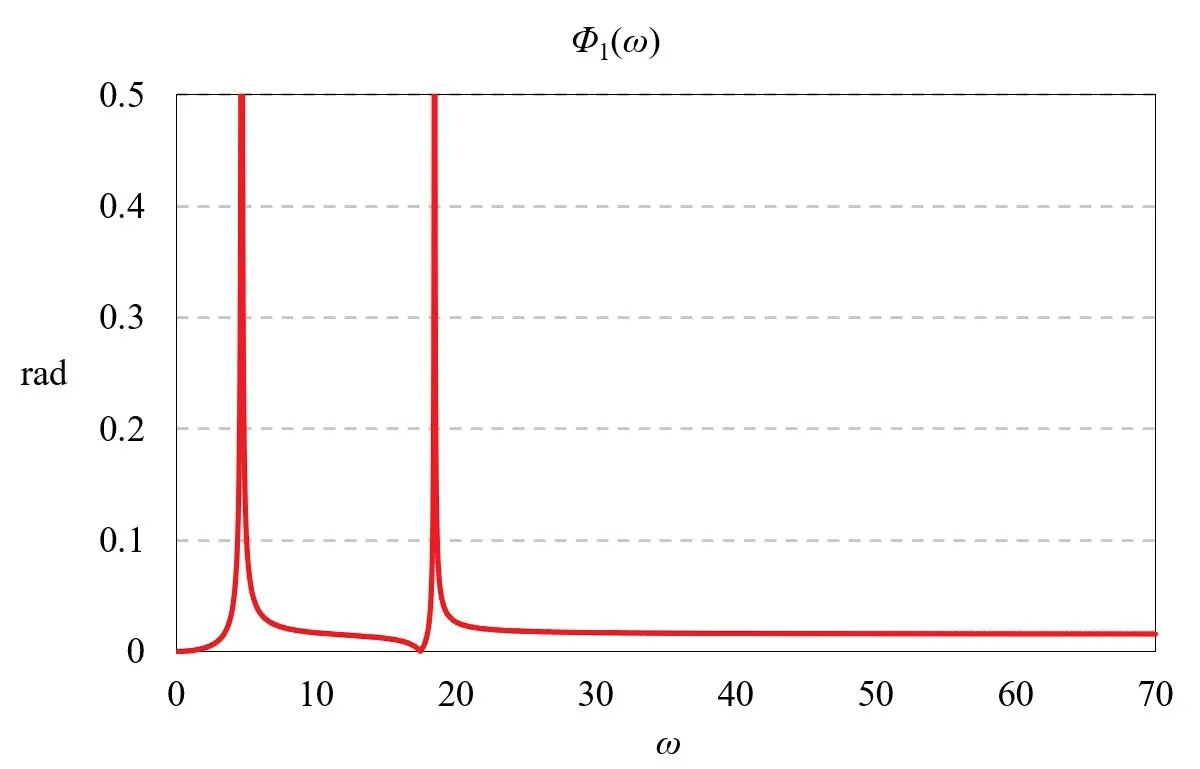
图8 Φ1(ω)幅频曲线

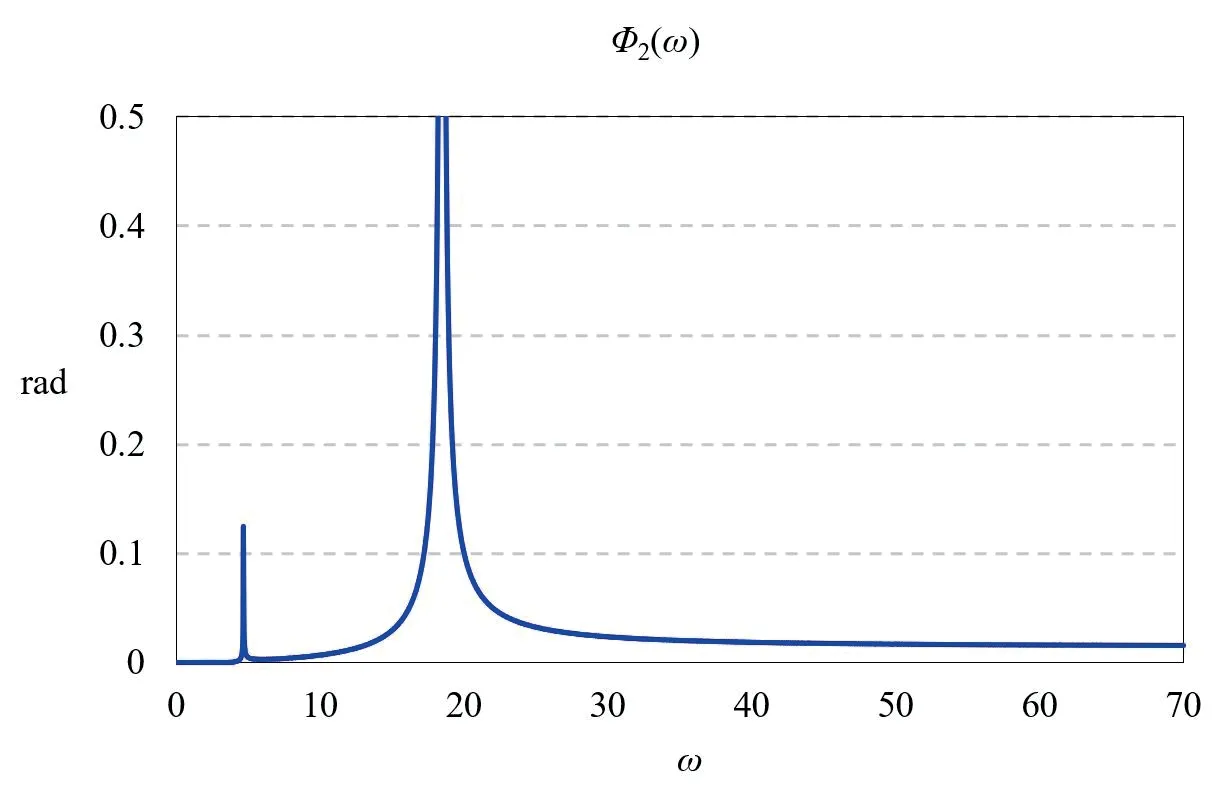
图9 Φ2(ω)幅频曲线

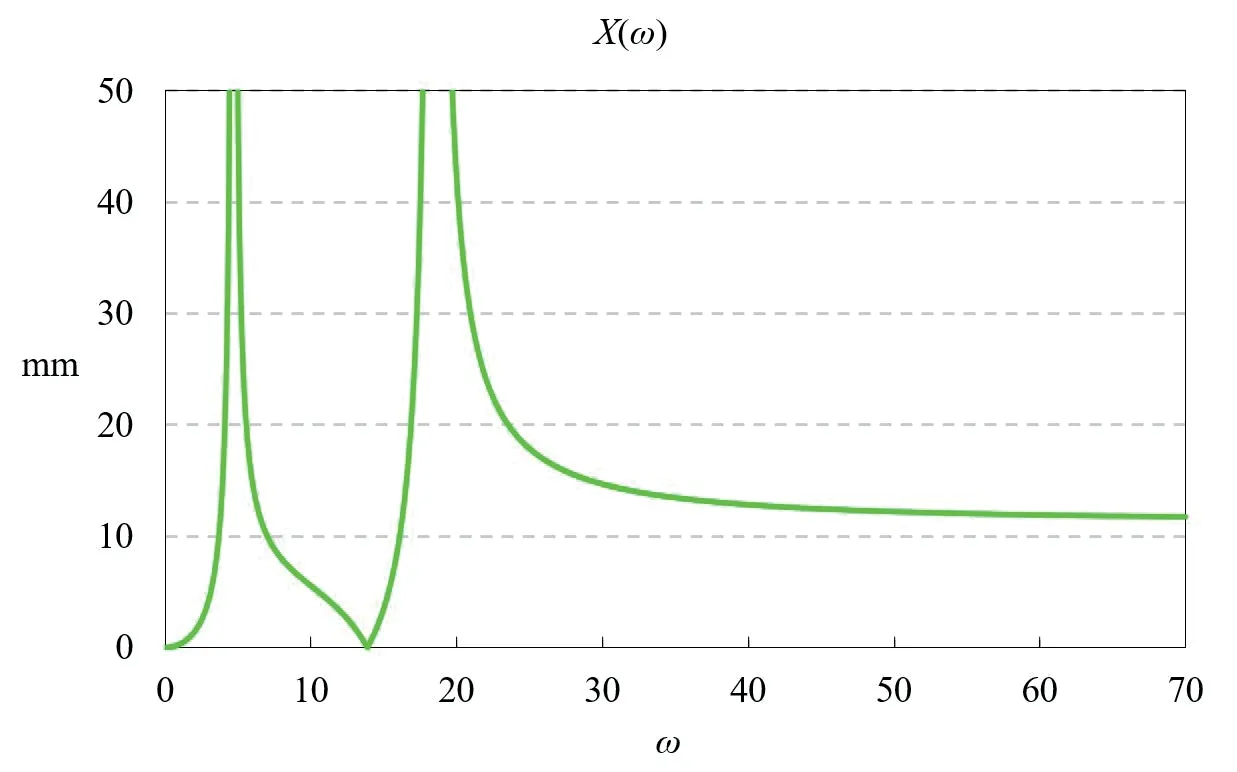
图10 合位移X(ω)幅频曲线

为考察平衡环平衡力对悬挂系统振动的影响，分别假设平衡环内液体的抗偏心质量为0 kg、0.1 kg、0.2 kg、0.3 kg、0.4 kg、0.5 kg，桶部件顶端合位移X(ω)的幅频曲线见图11。

从分析结果可以看出，主要由第一阶模态（单摆模态）贡献的振动幅值与偏心力、平衡环平衡力的力差成正比，主要由第二阶模态（质量-弹簧模态）贡献的振动幅值与偏心力、平衡环平衡力相对于吊杆-桶部件铰接点的力矩差成正比。

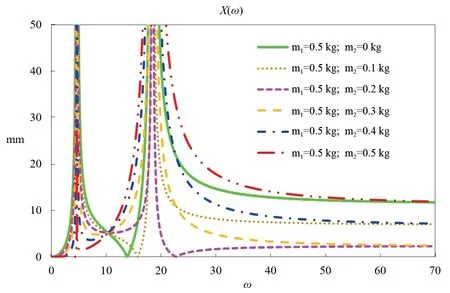
图11 不同平衡环抗偏心质量工况下合位移X(ω)幅频曲线

3.3 吊杆安装位置对系统振动的影响

为考察吊杆安装位置（吊杆-桶部件铰接点位置）对悬挂系统振动的影响，分别将桶部件向上移动10 mm、20 mm，向下移动10 mm、20 mm（随之发生变化的参数包括h、h1、h2、Jo'），第一、二阶固有频率随之发生变化，各种工况下的系统固有频率见表1。假定平衡环抗偏心质量为0.3 kg，桶部件顶端合位移幅频曲线见图12。

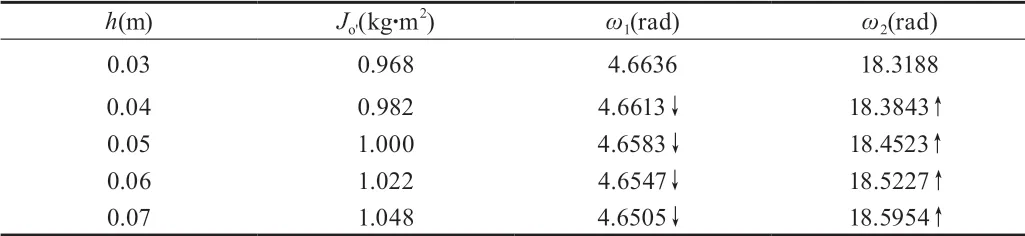
表1 固有频率对比

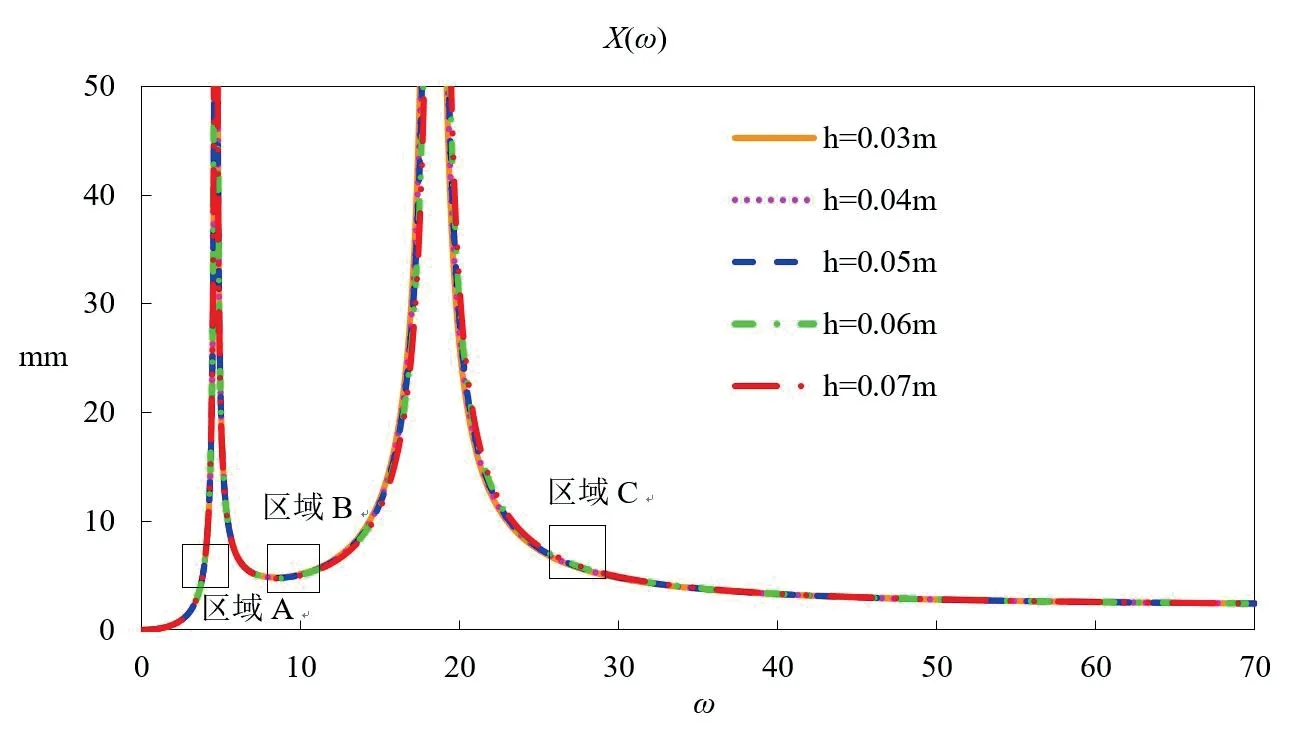
图12 不同吊杆安装位置工况下合位移X(ω)幅频曲线

从图12、图13的幅频特性曲线可以看出：

（1）在低频（第一个共振点之前）和高频（第二个共振点之后）阶段，桶部件质心越靠近吊杆-桶铰接点，桶部件振幅越小；在中间阶段（第一、二个共振点之间），桶部件振幅与吊杆安装位置没有明显的一致性。总体而言，吊杆安装位置的小幅变更对桶部件的振动影响幅度较小。

（2）桶部件质心靠近吊杆-桶铰接点，第一个共振点幅值升高，第二个共振点幅值降低。

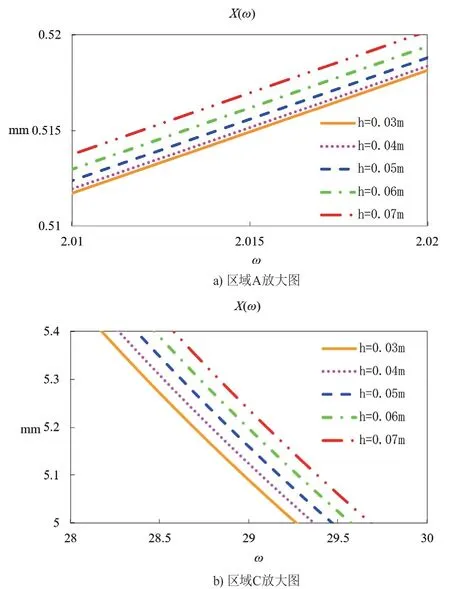
图13 对图12部分区域放大图

3.4 理论分析

从3.1节的论述中可知，通过所建平面二自由度模型求解出的模型第一阶固有频率值与单摆固有频率理论公式求解值一致，简化模型与基本理论吻合，本节进一步从理论分析的角度解释3.2节、3.3节所得结论的合理性。波轮洗衣机有两类铰接点：吊杆和箱体铰接点、吊杆和外桶铰接点，均可视为球铰接，球铰只传递力而不可传递力矩，所以内桶衣物偏心产生的激励力，可使桶部件产生平动，而激振力相对于吊杆和外桶铰接点的力矩可使桶部件产生转动，这与3.2节所得结论一致。当桶部件的质心位置越靠近吊杆-外桶铰接点，平动和转动模态的耦合程度越小，桶的振动越小，这与3.3节所得结论也是吻合的。以上理论分析进一步佐证了所建波轮洗衣机悬挂系统平面二自由度模型的合理性。

4 结论

（1）将波轮洗衣机悬挂系统的运动简化为平面二自由度运动，从而建立了其二自由度运动方程，先是对悬挂系统的振型进行了分析，然后绘制了两个自由度及其合位移的幅频特性曲线，得到了桶部件顶端位移的计算公式，可以据此进行桶部件稳态振幅的计算；

（2）根据所建立的运动方程，对波轮洗衣机悬挂系统的动力学特性进行了研究，分别探讨了平衡环平衡力和吊杆安装位置对桶部件振动的影响。通过对平衡环平衡力的研究，得出以下结论：主要由第一阶模态（单摆模态）贡献的振动幅值与偏心力、平衡环平衡力的力差成正比，主要由第二阶模态（质量-弹簧模态）贡献的振动幅值与偏心力、平衡环平衡力相对于吊杆-桶部件铰接点的力矩差成正比。

（3）分析中未考虑平衡环液体偏移量与桶部件振幅的双向耦合问题，根据所推导的桶部件顶端合位移的稳态振幅公式，可以结合平衡环内液体偏移量与平衡环液体质心之间的关系[3]，对平衡环液体偏移量和桶部件振幅进行迭代计算，从而最终确定各种工况下达到稳态阶段时平衡环内的液体偏移量。