体外预应力节段预制拼装混凝土梁疲劳试验研究

唐细彪 章 龙

(1.桥梁结构安全与健康国家重点实验室 武汉 430034； 2.中铁桥研科技有限公司 武汉 430034)

桥梁节段预制拼装梁施工技术以其生产效率高、施工质量好等优点，在国内外发展较快且应用较多。国内外学者针对节段结构受力行为也进行了广泛研究，且取得了一定的成果。然而，针对桥梁节段预制胶接拼装的破坏试验研究相对较少，仍有一些问题需要深入研究，如体外预应力预制拼装系统的抗疲劳、系统抗疲劳薄弱部位等。为此，本文开展预制拼装节段梁疲劳研究，通过对比国内外多种疲劳荷载计算方法，确定疲劳等效荷载；同时进行节段预制拼装梁的抗疲劳理论分析及疲劳试验，以验证结构设计的合理性和安全性。

1 工程实例

华岩隧道西延伸段桥跨采用节段预制拼装施工技术，上部结构采用三(或四)跨一联布置，单跨跨径为30 m，采用单箱室结构，箱梁宽度为12.15 m，梁高为2 m，节段预制拼装梁典型断面构造见图1。节段预制拼装梁划分见图2。

图1 节段预制拼装梁典型断面构造图(单位：mm)

图2 节段预制拼装梁节段划分(单位：mm)

如图2所示，单跨箱梁共分为13个节段，节段两端设置凹凸交替的混凝土剪力键，并在接缝界面上涂刷环氧黏结剂，通过压力使各节段黏结成为整体。桥梁按全预应力混凝土构件设计，在箱梁内部设置8束φs15.20-27(31)体外索，通过对其张拉以提供连续梁结构预压力。

预制节段采用C50混凝土浇筑；体外索采用单丝环氧预应力无黏结钢绞线，转向器采用散束式转向器；单股钢绞线标准强度1 860 MPa，弹性模量Ep=1.95×105MPa，张拉控制应力为60%标准强度；环氧黏结剂抗压强度12 h时不小于40 MPa，抗压强度7 d时不小于80 MPa，抗折强度7 d时不小于40 MPa。

2 模型设计

依据相似理论对预制拼装箱梁实桥进行模型设计，取受力相对不利的中跨作为研究对象。为真实反映实桥受力情况，且试验荷载不致于过大造成加载困难，确定模型在高度、长度，以及宽度方向取1∶3的比例尺，同时模型截面取实桥箱形截面的一半，设计为左右对称的工字形截面。最终模型纵向长度约为10 m，梁高为0.667 m、宽为1.933 m。

模型混凝土、钢筋及钢绞线材料与实桥完全一致。体外预应力束设计按与实桥效应一致为原则，缩尺后采用四孔预应力束布置。锚块、转向块、接缝及剪力键等细节部位与实桥一致，尺寸严格按照1∶3比例进行缩尺，模型尺寸和节段划分示意见图3。

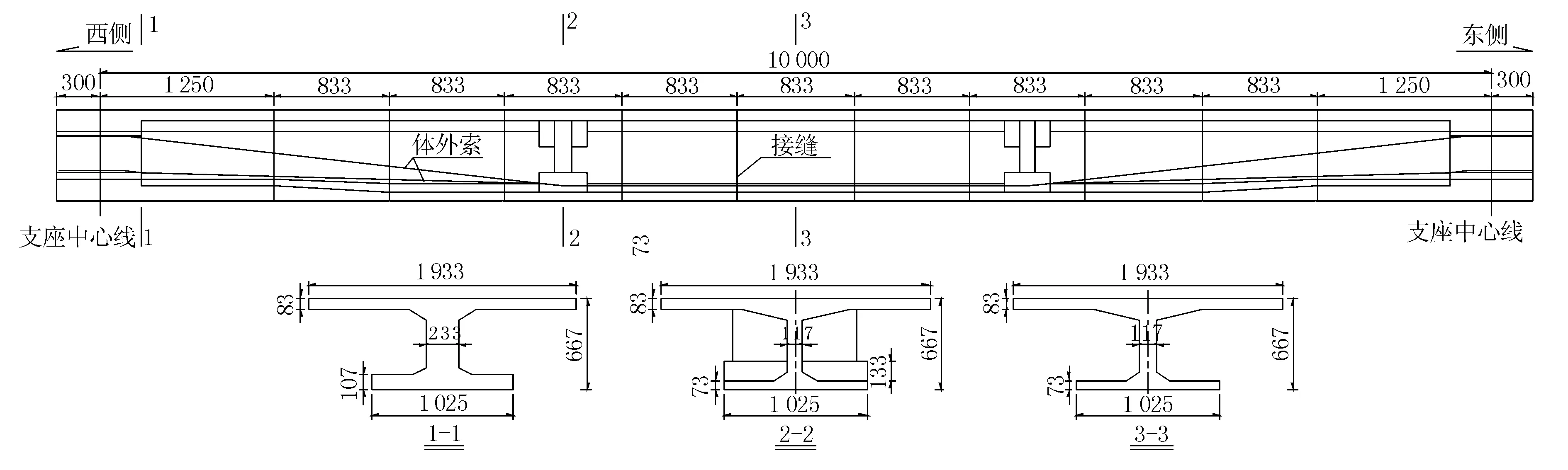
图3 模型尺寸和节段划分(单位：mm)

3 疲劳荷载

通常来说，进行构件的疲劳研究，首先要确定构件在运营寿命下的疲劳荷载。桥梁疲劳荷载一般考虑桥梁结构运营时各种实际车辆通行情况，在此基础上进行车辆对桥梁造成的累计损伤计算得到。而新建桥梁由于缺乏交通资料，往往是根据地区地理位置及发展规划进行交通量预测，或者根据情况类似的已建成桥梁进行交通量调查，采用疲劳累计损伤理论，以评判桥梁在设计寿命期内抗疲劳能力[1]。

国外规范(美国公路桥梁设计规范AASHTO、英国桥梁设计规范BS5400、欧洲规范Eurocode1)中均给出了关于公路桥梁疲劳荷载的规定。而早前在国内，公路桥梁规范均未对疲劳荷载计算作出具体规定，仅在JTJ 025-1986 《公路桥涵钢结构及木结构设计规范》中提到：“验算疲劳强度时，可根据桥梁实际行车情况，选用实际经常发生的荷载组合中的车辆荷载进行计算。”直到在JTG D60-2015 《公路桥涵通用设计规范》中，才详细给出了3种标准车模型，以供桥梁相关构件进行疲劳荷载计算，为桥梁疲劳设计提供依据。本文分别对各国规范的疲劳荷载谱进行归纳及对比分析，以确定本项目的疲劳荷载取值，作为抗疲劳理论分析及荷载试验的依据。

3.1 BS5400疲劳荷载谱

BS5400将公路荷载谱分为3种类型：典型车、标准疲劳车、轴重车。其中典型车是以英国20世纪70年代对本国公路干线运营交通量调查为依据，将车辆分为25种车型。同时规定这25种典型车的车重、轴距，以及出现的频率，以此作为桥梁疲劳荷载的依据。标准疲劳车由典型车简化而来，通过对典型车活载频值进行应力变幅计算，最后等效为一种“标准疲劳车”，该标准车轴重80 kN，采用4轴，总重为320 kN。轴重式车辆主要是针对影响线很短的构件(比如桥面板)，车辆每个轴重加载都会产生一个应力循环，为此BS5400专门提供了一个以轴重形式的活载频值谱，同时给出每个车道的年运营车辆数和布置位置。

3.2 AASHTO疲劳荷载谱

AASHTO疲劳设计指导性规范中给出了一种货车加载车作为标准车用于疲劳检算，该疲劳车采用3轴，总重为325 kN。不过该规范没有给出通用的荷载频值谱，而是规定疲劳加载的荷载频率应取单车道日平均货车交通量(ADTTSL)，在缺乏资料的情况下，该值建议按下式计算：ADTTSL=P×ADTT。式中：ADTT为桥梁在设计寿命期内单向日平均货车量；P为多车道桥梁在单车道内货车交通量的占比。

3.3 国内疲劳荷载规定

JTG D60-2015 《公路桥涵设计通用规范》规定，在疲劳检算时可按3种计算模型进行。计算模型I采用等效的车道荷载，集中荷载为0.7Pk(Pk为集中荷载标准值)，均布荷载采用0.3qk(qk为公路车道荷载均布荷载标准值)，同时采用该计算模型应考虑多车道的影响；该模型对应于无限寿命设计方法。计算模型II采用双车模型，两模型车轴距与轴重相同，总重均为405 kN，其单车的轴重和轴距布置见图4。计算模型III采用单车模型，其单车的轴重和轴距布置见图5。该计算模型III车重最重，轮数较少，适用于正交异性板、横隔板(梁)、纵梁等直接承受车轮荷载构件的疲劳验算。

图4 疲劳荷载计算模型II

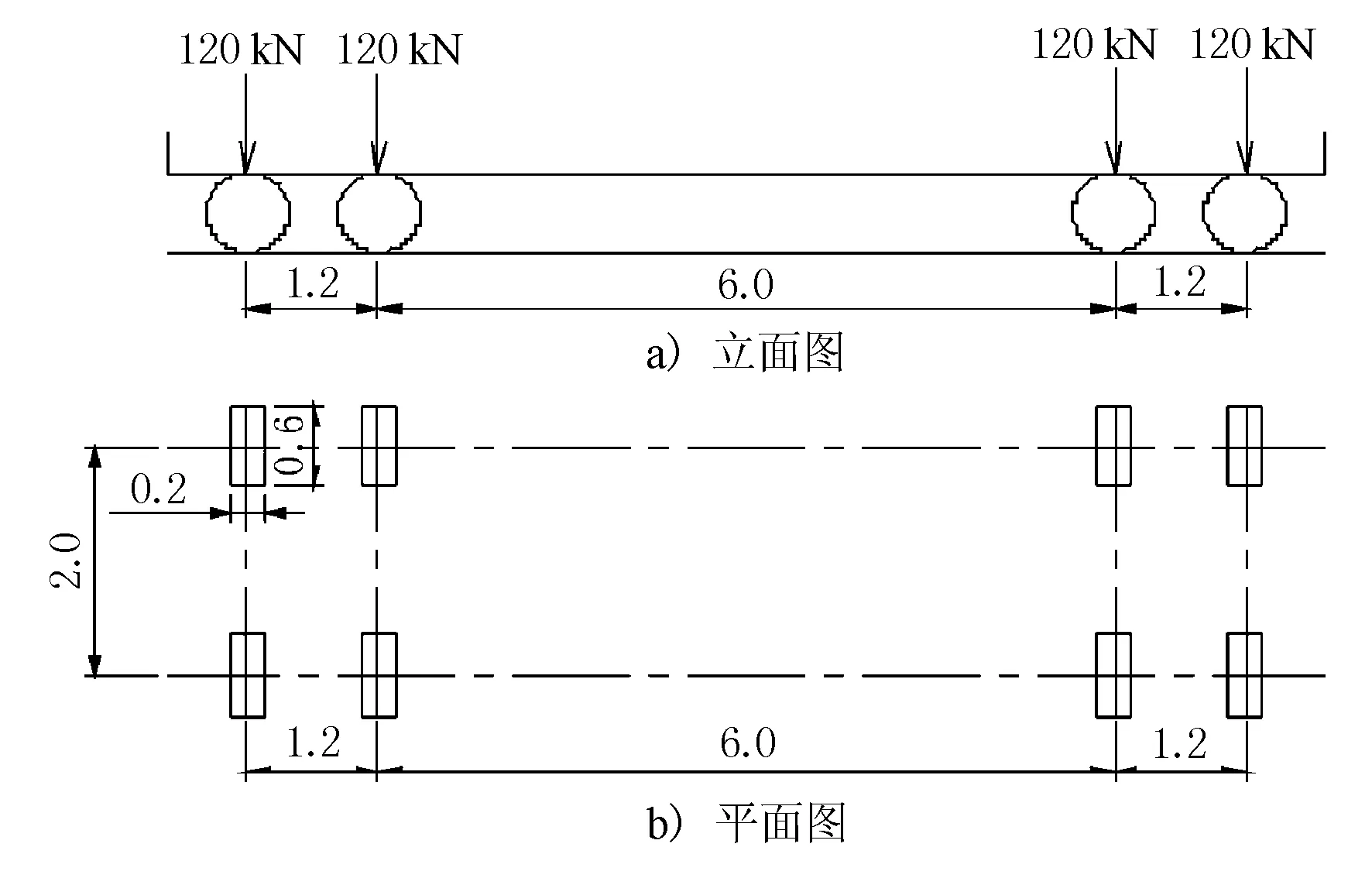
图5 疲劳荷载计算模型III(尺寸单位：m)

3.4 疲劳试验荷载计算

从上文可以看出，各国都是根据本地区的实际情况，提供各种标准车荷载用于疲劳检算。通过对比，我国公路桥规的计算模型II疲劳加载标准车的轴重最大，可以认为相同次数的循环加载下结构产生的应力幅可能最大，受力最为不利。因此，在进行本文项目节段预制拼装梁抗疲劳分析时，采用国内公路桥规规定，结果偏于安全。

在进行疲劳检算时，首先以预制拼装箱梁跨中弯矩为目标，求得该位置弯矩影响线,见图6。

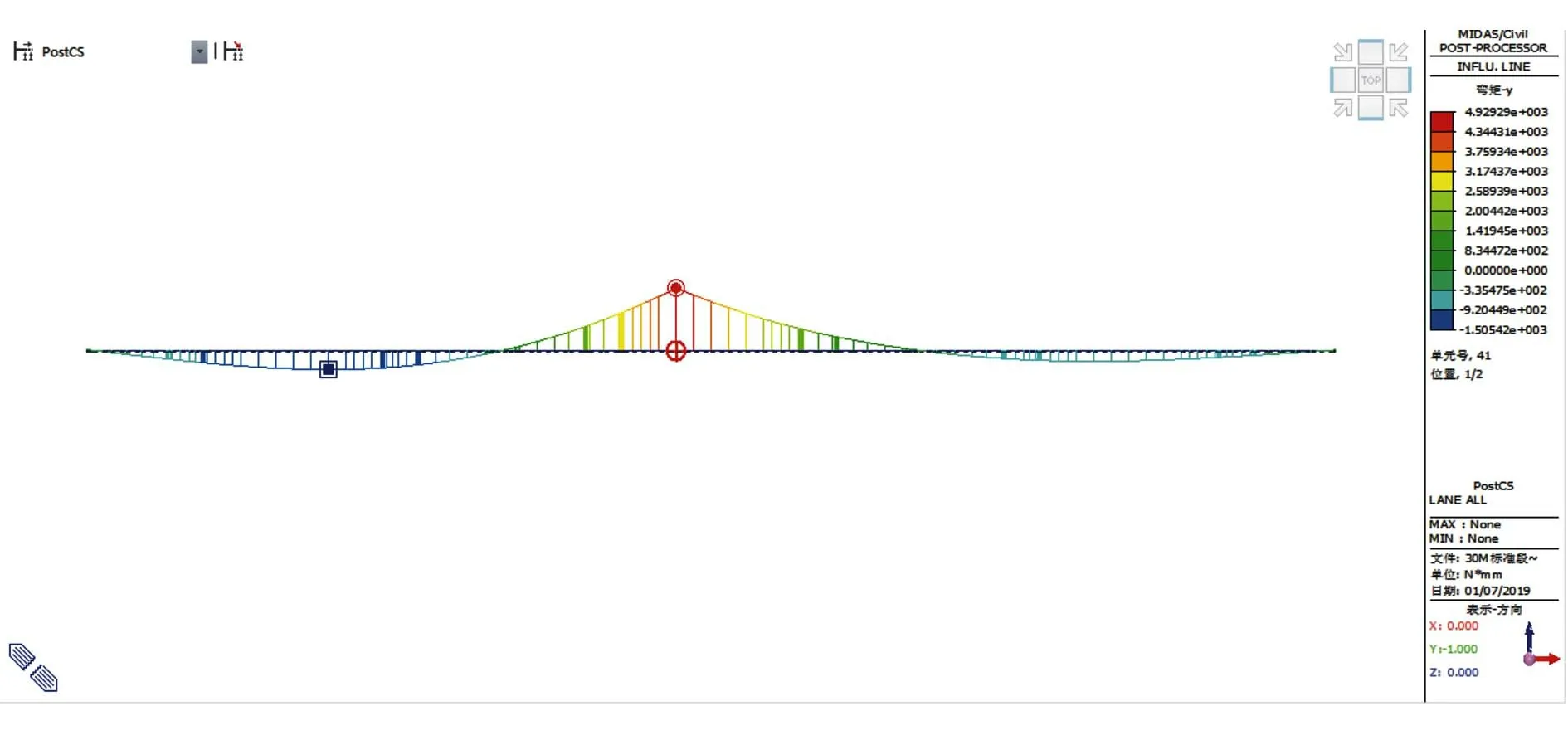
图6 节段预制拼装梁跨中部位弯矩影响线

由图6可见，加载车辆通过桥梁时，跨中部位将经历1次应力循环。在此基础上，分别施加规范中模型I与模型II对应的车道荷载，可计算得到跨中部位弯矩幅值。另外，为保证偏于安全，取最大弯矩幅值作为疲劳试验依据。通过计算得到模型I、II加载后对应的弯矩幅分别为6 138.6，2 449.2 kN·m。因此，取6 138.6 kN·m作为疲劳试验荷载依据。

4 疲劳理论分析

4.1 混凝土抗拉、抗压疲劳问题

对于全预应力混凝土结构构件来说，在设计使用荷载作用下，混凝土上、下缘均不会出现拉应力，更不会出现开裂[2]。因此，本结构混凝土无抗拉疲劳问题。

对于混凝土的抗压疲劳性能，研究者通常通过大量的试验，根据试验结果并通过概率统计的方法将试验结果组织成简单易用的形式，常见的有S-N曲线等。同时研究得到，只要混凝土构件最大压应力不超过某个规定限值，即可满足耐久性要求。另外，混凝土构件疲劳强度还与荷载特征有关，即重复荷载下限值σmin与上限值σmax之比ρ(荷载循环特征系数)有关[3]。铁道部科学研究院[4]曾通过试验测得抗压疲劳强度为(0.55～0.65)fck，对于较低等级的混凝土，则为(0.4～0.5)fck。在国外研究成果中，也较多以混凝土疲劳极值的形式以供参考。比较典型的有瑞士洛桑桥梁与结构工程协会(IABSE)报告[5]，给出受压混凝土疲劳寿命的计算式，其中当σmin=0，N=200万次时，推断出受压疲劳强度为0.63fck。

通过桥梁整体分析，本文研究的结构在使用阶段受压区混凝土最大压应力为11.8 MPa，约为0.36fck，小于上述国内外研究成果的疲劳强度相关限值。另外根据GB 50010-2010 《混凝土结构设计规范》中表4.1.6规定，混凝土抗疲劳强度设计值按强度设计值乘疲劳强度修正系数γρ确定，其中γρ与疲劳应力比值ρc(构件疲劳检算时，截面同一纤维上混凝土的最小、最大应力)相关。由于本文结构受力以恒载为主，在考虑疲劳等效荷载后，在跨中位置的疲劳应力比值ρc远大于0.5，即抗疲劳强度设计值无须折减。因此，综合分析得到节段预制拼装梁混凝土抗压疲劳性能是满足相关要求的。

4.2 体外预应力钢绞线疲劳问题

体外预应力钢束一般在桥梁两端锚固，并通过在桥跨特定位置布置转向器，使其参与并提高结构承载力。在汽车活载作用下，梁体下挠变形使得体外束长度发生变化，进而导致钢束应力变化。待汽车活载卸载后，钢束应力则回归到原应力水平，这个过程即为应力循环。

在国外体外预应力疲劳研究方面，国际预应力混凝土协会FIP建议[6]，带锚具的整根预应力筋在上限应力σpmax=0.65fptk和循环次数N=2×106的条件下，能经受的应力幅度Δσp应不低于80 MPa。美国ACI215委员会建议，预应力筋σpmin在达到抗拉极限强度的60%时，在重复荷载作用下，钢绞线的应力变化幅度不得超过0.10fptk(若按标准预应力钢筋强度标准值1 860 MPa，该幅值为186 MPa)。在国内，长沙铁道学院[7]于1987年曾开展过7φs5钢绞线的不同应力幅的疲劳试验研究，其上限应力σpmin采用铁路桥规规定的最大值0.65fptk，应力幅Δσp分为采用50，100，150，200，250 MPa，通过2×106次循环荷载加载的钢绞线，其应力变化幅度基本在150 MPa以下，这与美国ACI215规定0.10fptk较接近。

一般认为，体外预应力束在各个自由段(即锚固点与转向块之间区域、转向块与转向块之间区域)内的应力值相等，活载应力变幅相对于体内束是小的。国内外均有研究表明[8]，在典型体外预应力桥梁中，体外预应力束的活载应力变幅要小于25 MPa。结合本桥，通过计算体外束的应力幅值为15 MPa，该值与前文研究成果基本相符。另外，JT 329.2-1997 《公路桥梁预应力钢绞线用锚具、连接器试验方法及检验规则》要求，钢绞线锚具组装件应能经受住200万次的疲劳试验，疲劳幅为80 MPa，也远大于本研究对象的体外束应力幅15 MPa。因此，可以认为本桥预制拼装箱梁体外预应力钢绞线的抗疲劳能力具有较大余量，不控制结构的长期耐久性。

5 疲劳试验

虽然从理论分析上，排除了结构各组成材料单独出现疲劳破坏的可能性，但考虑到在运营过程中是否出现局部应力重分布，或者3种材料作为一个整体，是否出现疲劳损伤，还需进一步验证，因此有必要开展节段预制拼装试验梁模拟疲劳试验。

5.1 试验加载

依据相似理论，将前文疲劳弯矩幅计算值6 138.6 kN·m，换算到模型为113.7 kN·m。由于无法直接施加弯矩，可通过对跨中施加竖向力实现。同时为保证跨中承受纯弯矩受力，采用两点加载。为使试验结果偏安全，将该竖向力乘以1.2倍的安全系数。试验在MTS-1000 kN万能试验作动器下进行，加载次数为200万次。加载示意图见图7。

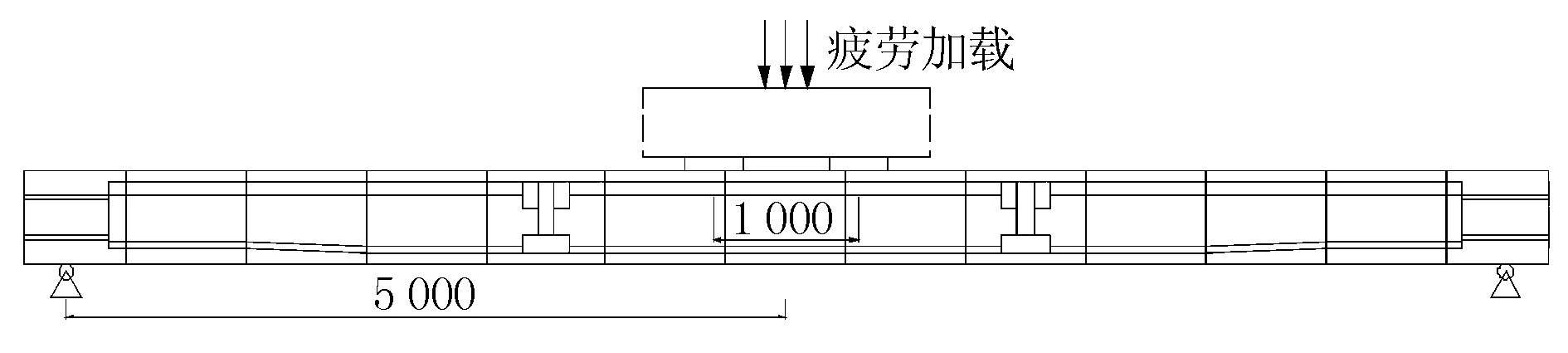
图7 节段预制拼装试验梁模拟疲劳试验加载示意图(单位：mm)

5.2 试验结果

疲劳试验测点主要针对跨中、跨中接缝附近(距接缝100 cm)等典型断面，测点布置见图8。由于测试数据较多，本文仅给出2号接缝顶板纵向应变数据予以说明。测点每隔约20万次的应变变化见图9，200万次加载后测点的应变荷载曲线见图10。

图8 节段预制拼装试验梁测点布置图(单位：mm)

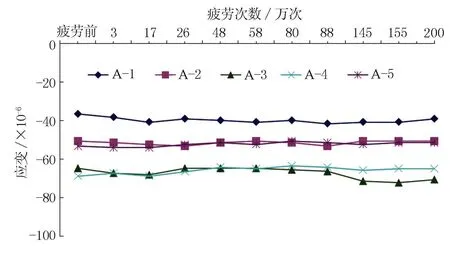
图9 2号接缝各测点每隔约20万次的应变变化

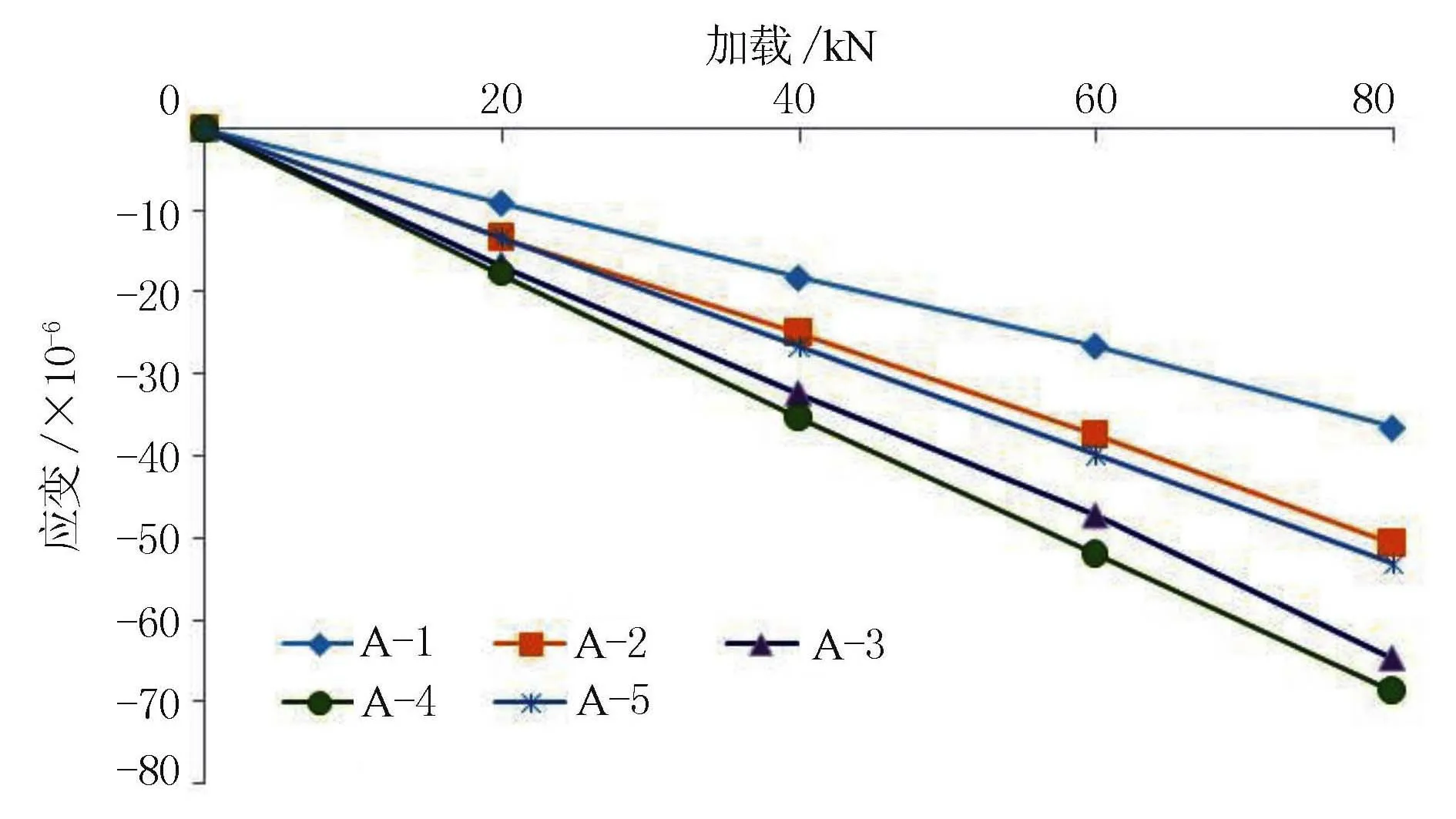
图10 200万次加载后测点应变荷载曲线

从图9、图10可以看出，2号接缝顶板附近各测点在每隔20万次疲劳荷载加载下，应变变化较小，基本呈水平直线状。在经过200万次加载后，测点应变与荷载应变呈现良好的线性关系，表明结构力学特性并未随循环次数的增加而发生明显改变，仍处于弹性受力状态。

试验结束后经全面检查，节段预制拼装模型结构也未见明显受力裂缝和缺陷，进一步验证了该结构具有足够的抗疲劳性能，满足设计要求。

6 结论

1) 对比分析国内外规范关于疲劳荷载的计算方法，表明我国公路桥规提供的计算模型II轴重最大，相同次数的循环加载下结构产生的应力幅最大，受力最为不利，最适宜作为节段预制拼装梁疲劳试验疲劳荷载计算依据。

2) 通过理论分析，体外预应力节段预制拼装梁包含的混凝土和钢绞线等构件抗疲劳能力具有较大余量，不控制结构的耐久性。

3) 模型在200万次疲劳加载后,各部位均未发现疲劳裂纹,模型的力学特性未随循环次数的增加而发生明显改变，验证了体外预应力节段预制拼装梁结构疲劳设计的合理性和安全性。