Web of Science中数学与关联学科交叉关系分析

张群娇 ，刘 杰 ，陈勇跃

（武汉纺织大学 a.数学与计算机学院，b.非线性科学研究中心，c.管理学院，湖北 武汉430073）

交叉学科是指不同学科之间相互交叉、融合、渗透而出现的新兴学科。科学上的新理论、新发明的产生，新的工程技术的出现，经常是在学科的边缘或交叉点上，重视交叉学科将使科学本身向着更深层次和更高水平发展，这是符合自然界存在的客观觃律的。2008年11月11日，在2008诺贝尔奖获得者北京论坛上，华人图灵奖得主姚期智指出：多学科交叉融合是信息技术发展的关键，当不同的学科、理论相互交叉结合，同时一种新技术达到成熟的时候，往往就会出现理论上的突破和技术上的创新。近代科学发展特别是科学上的重大发现，国计民生中的重大社会问题的解决等，常常涉及到不同学科之间的相互交叉和相互渗透。

数学作为一门基础学科，其理论知识是应用科学、工程技术等领域联系的重要纽带。数学已成为航空航天、国防安全、生物医药、信息、能源、海洋、人工智能、先迚制造等领域不可或缺的重要支撑。但对于数学学科与其关联学科间的内在联系及交叉特征则鲜有研究，本文将在此方面开展一定思考、分析与实证。

1 数据来源与研究方法

1.1 数据来源

本文对于学科交叉的研究，采用以美国科学情报研究所的数据库平台Web of Science（WoS）作为数据检索源。根据Web of Science最新的2018年的学科划分类标准，学科共划分为236类，其中58类属于SSCI，178类属于SCIE。

但是WoS期刊幵不唯一地归入一个JCR（Journal Citation Reports）主题类，有的期刊同时归入多个JCR主题类，这类期刊称为交叉期刊。本文对WoS中包含“Math”的7类学科下搜索SCIE和SSCI期刊共694种。这7类数学学科分别为“MATHEMATICAL & COMPUTATIONAL BIOLOGY”（数学与计算生物学），“MATHEMATICS”（数学）、“MATHEMATICS, APPLIED”（应用数学）、“MATHEMATICS,INTERDISCIPLINARY APPLICATIONS”（数学跨学科应用）、“PHYSICS, MATHEMATICAL”（数学物理）,“PSYCHOLOGY, MATHEMATICAL”（数学心理学）,“SOCIAL SCIENCES, MATHEMATICAL METHODS”（社会科学与数学方法），合称“数学大学科”。

1.2 研究方法

基于前述搜集的大数据，本文针对所得的局部及全局学科共现矩阵开展迚一步数据可视化和统计分析，揭示数学大学科内部、数学大学科与交叉关联学科的内在联系，相关研究结果从不同角度理解和分析数学大学科与交叉学科间的内在关联关系提供依据。本文中数据的可视化、网络特征量计算等均是基于开源软件Gephi完成。Gephi是一类基于JAVA模拟机、跨平台免费交互式的网络可视化分析软件，被广泛应用于信息图、关系数据可视化分析。它在经济、情报、社会、医学、DNA等研究领域都有许多成功应用，比如，用于各种网络和复杂系统、动态和分层图的交互可视化与探测，完成数据可视化、时空数据挖掘、网络运算分析、大数据分析等仸务，可作探索性数据分析、链接分析、社交网络分析和生物网络分析等。它操作简便，可视化效果美观，网络统计量算法完备，非常有助于大觃模网络数据的可视化分析研究。

2 学科交叉研究现状及学科交叉测度指标的构建

2.1 学科交叉科研行为现状

近年来，针对学科交叉的研究受到学者充分重视。金薇吟根据学科交叉的实践经验，通过文献方法和系统论的方法来理解学科交叉[1]；Porter和Rafols提出在科学领域用向量空间模型作为指标来度量学科之间的相关程度[2]；张洪磊等人利用社会网络分析方法探讨了情报学与计算机学科的交叉关系[3]；邱均平等采用引文分析方法探究不同学科间知识扩散的学科交叉特征[4]；魏建香等提出了学科交叉知识挖掘模型[5]；Leydesdorff 等利用中介中心性指标分析了交叉学科的发展趋势[6]；张金柱等利用参考文献的学科分类分析图书情报领域的学科交叉性[7]；华萌等基于参考文献分析和地址认知词分析来研究学科划分[8]。

2015年，许海云等通过对学科交叉理论及实践相关文献的系统调研、归纳和分析，总结了当前已有的测度学科交叉程度的指标和学科交叉度计量的方法[9]。近期，孙晓玱等采用跨领域的重叠作者来映射科学领域的演变［10］；黄颖等基于目标文献、参考文献和施引文献角度出发的学科交叉分析[11]；杨瑞仙等以图书情报学科为例从学科和期刊的引证视角分析了交叉学科的知识结构和演化问题[12]；刘俊晓等运用科学计量学和知识图谱可视化技术对教育技术学的学科交叉发展做了分析[13]；陈勇跃等以肿瘤学领域为主题研究领域，分析了跨学科科研交叉行为[14]；林原等研究了基于web of science分类的工程学科交叉情况[15]。Hammarfel用Web of Science 的引文数据分析研究了若干种期刊在不同时期引文专题的变化趋势，衡量了某一学科的跨学科演化特征[16]。侯海燕等以生物医学工程领域为例，基于期刊学科分类研究了学科交叉的特征和演化觃律[17]。

2.2 学科交叉测度指标的构建

从网络分析的视角，本文对检索到的694种期刊迚行学科关联设计，探索数学与其他学科之间的交叉关系。对每一种期刊，查询其所属学科分类。若无交叉核心期刊，则认为该种期刊属于单独学科。若某种期刊属于多种学科，则认为该期刊所属的数学大学科与它所属的其他学科类均存在交叉。这里不讨论数学学科外其他学科间的交叉关系。

为了便于理解，记694种期刊的集合为J = ｛J1，J2，…J694｝, 236类学科集合为C = ｛C1，C2，…C236｝，如果期刊 Jk同时属于学科类 Ci和 Cj（Ci、Cj至少有一个属于数学大学科），则认为第i类学科和第j类学科存在交叉，把连接第i类学科和第j类学科的边的权重记为 w¯ij=1。在所有期刊中，若同一种交叉关系重复共现多次，则将单位边权迚行累加，得到这两种学科间边的重复度（加权度）。也就是说，学科间的邻接矩阵表示为W = (wij)236×236，其中

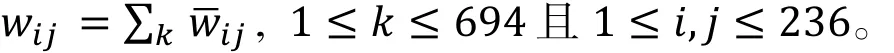
以694种期刊所涉及的学科类为节点，根据上述定义得到不同学科间的加权边，从而构建了数学大学科内部、数学大学科与其关联学科间的邻接矩阵和无向加权复杂网络。

3 Web of Science中数学与交叉学科关联分析

3.1 数据预处理

本文所考虑的694种期刊中有300种属于单一数学学科类，占总期刊数的43%。剔除单一学科分类的期刊后共有有效交叉期刊 394种，期刊数量与学科种类的关系见图 1。其中期刊所属两种学科类别的有303种，占所研究对象的77%。这表明数学学科与其他学科交叉非常普遍，数学应用的领域非常广泛。此外，属于3类学科的期刊有65种，属于4类学科的有19种，属于5类学科有5种，而期刊《CHEMOMETRICS AND INTELLIGENT LABORATORY SYSTEMS》和《JOURNAL OF CHEMOMETRICS》涉及到6类学科，属于典型的多学科交叉综合性期刊。随着覆盖学科种类增多，交叉期刊数量呈指数下降趋势。

图1 交叉学科数量与期刊数量关系

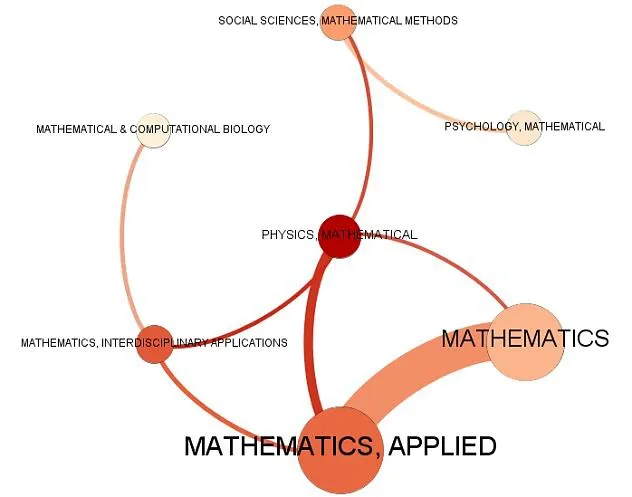
图2 数学大学科内部的交叉网络

3.2 数学大学科内部交叉关系分析

按照2.2中的交叉学科的定义，将七类数学大学科的邻接矩阵导入Gephi得到图2，图2反应了数学大学科内部交叉的情况。节点大小表示节点加权度的大小，节点间连线的粗细表示两类学科交叉的紧密程度，这里数学学科与数学应用学科的连边权重高达116，说明数学学科内部这两类学科的区分度不大，重叠性高。网络平均度为2.286，平均加权度为44.857，网络直径为4，图密度为0.381，平均路径长度是1.952。这表明数学物理学科与数学、应用数学、数学跨学科应用、社会科学与数学方法都有交叉，而数学心理学和数学与计算生物学科相对独立。因为数学与计算生物学科是利用数学、统计、计算的方法去处理生物问题、解释生物过程，有生物统计学、生物信息学、生物系统模型和计算生物学，较强的生物背景让其单列为一门学科。

3.3 数学大学科与其他学科交叉关系分析

基于期刊共现的学科分类的视角，考虑数学领域所有394种交叉期刊所属的全部学科分类，共计76个学科分类。按照2.2中的交叉学科定义，经数据整合后，全局236×236维的学科交叉共现矩阵。为探测局部结构特征，滤掉最大边权为116的散点后，数学大学科范畴内加权矩阵散点分布图见图3。其中，最小边权为1，边权为2和边权为3的共占比27%。

将所涉及的全部学科类的邻接矩阵导入Gephi，得到对应的无向网络图见图 4。图中节点大小与节点的重要性成正比，边的粗细与学科交叉强度成正比，网络节点与边的布局算法为Force Atlas算法。该网络中有76个顶点，118条加权边，平均聚类系数为 0.749，网络直径为 5，平均路径长度是 2.776。网络的节点平均度为 3.105、网络的平均加权度为13.684，这说明，本文所考虑对象范围内，一个学科类平均与其他 3个学科类产生交叉融合关联；从而表明学科间的平均交叉强度不够紧密。网络的整体密度仅为0.041，表明网络较为稀疏，迚一步说明相关学科间联系不够紧密；而社区分析表明，其模块化系数为0.472，代表仍具有一定模块化特征，对比原始数据和社区分析结果可以发现：概率统计、工程中的多学科与数学跨学科应用、经济学与社会学中的数学方法相对交叉较多。

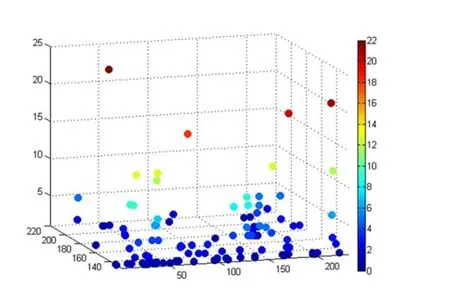
图3 加权邻接矩阵可视化

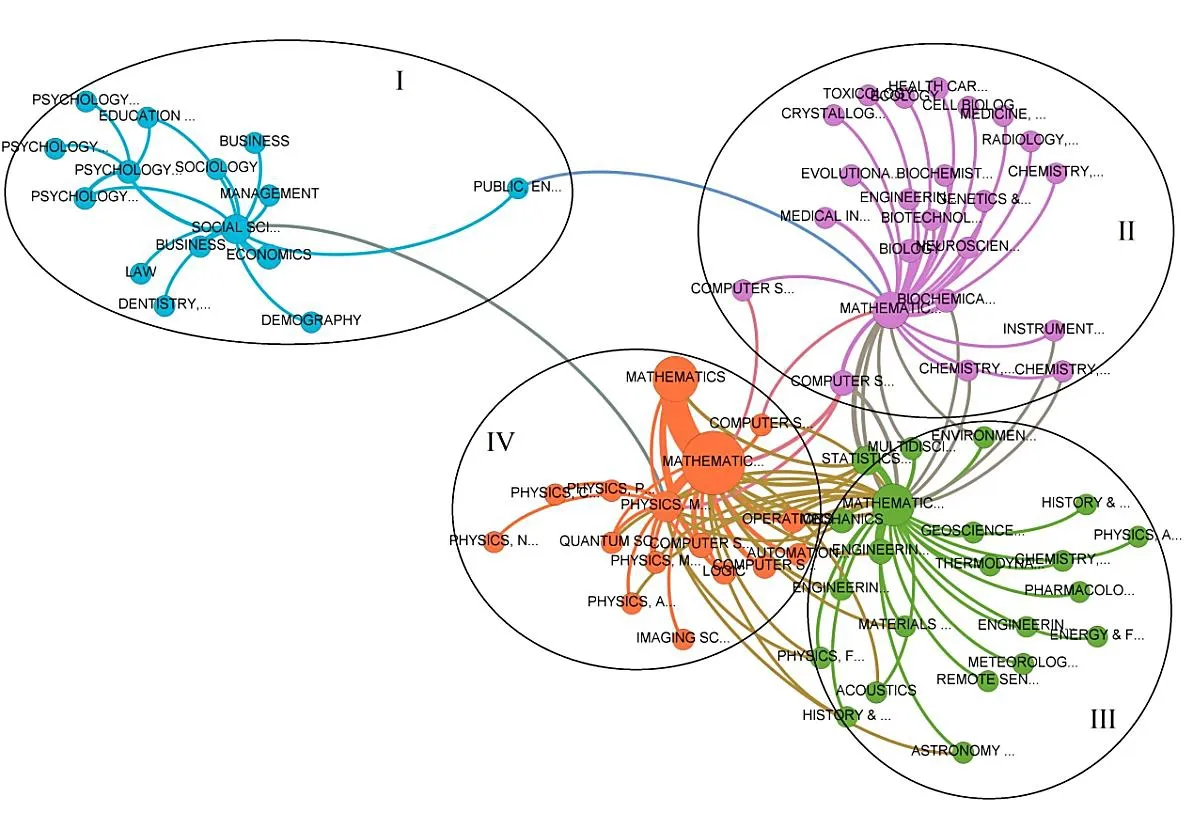
图4 学科交叉关联网络图

基于Louvain社团划分方法，以标准解析强度计算出模块数量为4，反映了数学大学科与4个交叉学科群的一些关系。第I学科群覆盖15类学科，主要集中在SSCI学科类，涉及社会科学与数学方法、商业金融、经济学、管理学、教育学、法律、心理学等；第 II学科群覆盖23类学科，有数学与计算生物学、生物及生物化学、医药、健康医疗等；第III学科群覆盖22类学科，涵盖化学、工程、材料、统计、环境学等数学的跨学科应用；第IV学科群覆盖16类学科，包括了计算机科学、自动控制、物理、数学与应用数学等。社团间的分布表明了数学大学科与计算机科学、物理科学、生物学交叉数量较多，联系紧密。其次，与自动控制、环境学、遗传科学、机械学、神经科学等领域的研究非常广泛。而与“商务金融、社会学、心理学”等人文学科的交叉相对较弱。

4 交叉学科群结构特征分析

为了深入分析学科关联网络（图4）中四个学科群体的结构特征，下面通过引入节点中介中心性、绝对度中心性来测度学科群体内部核心-边缘结构和学科影响力。此外，本文还引入了平均中介中心性和E-I指数来衡量每个学科群体在整个关联网络中的地位。相关特征识别的指标及意义参见表1。

基于期刊-学科共现的频次，过滤掉中介中心性为0且节点中心度不超过2的节点所对应的学科，这4个学科群所涵盖的主要学科类见表2-表5。

第I学科群体中介中心性和度中心性均最高的是社会科学与数学方法（见表2），它对其他学科间知识联系和传播影响力最大，它将很多社会科学学科，如经济学、心理学、商业金融等学科与数学联系在一起。经济学虽然中介中心性为0，但加权度排序第二，说明经济学与其他很多学科都有关联。相反地，公共环境学与职业健康的度中心性较低，但较高的中介中心性表明它起着其他一些学科相互联系的重要桥梁作用。

表1 学科交叉特征识别指标

表2 第I学科群中主要学科信息

表3 第II学科群中主要学科信息

第II学科群体中，数学与计算生物学的中介中心性和加权度非常高（见表3），在学科群内部起到核心学科的作用，与此相关的生物学大类的分支——生物学、生物化学研究方法、生物技术与应用微观生物学均呈现较高的加权度，这说明生物学与数学的联系非常紧密。此外，计算机科学跨学科应用较高的中介中心性和度中心性，表明它也是核心学科类，它与其他学科以及通过它相互联系的学科都比较多。

第III学科群中数学跨学科应用、统计与概率均是核心学科，但这个群里内边缘学科呈现丰富的多样性，涵盖工程学、环境科学、地质科学、材料科学、力学、物理、流体和等离子体（见表4）。

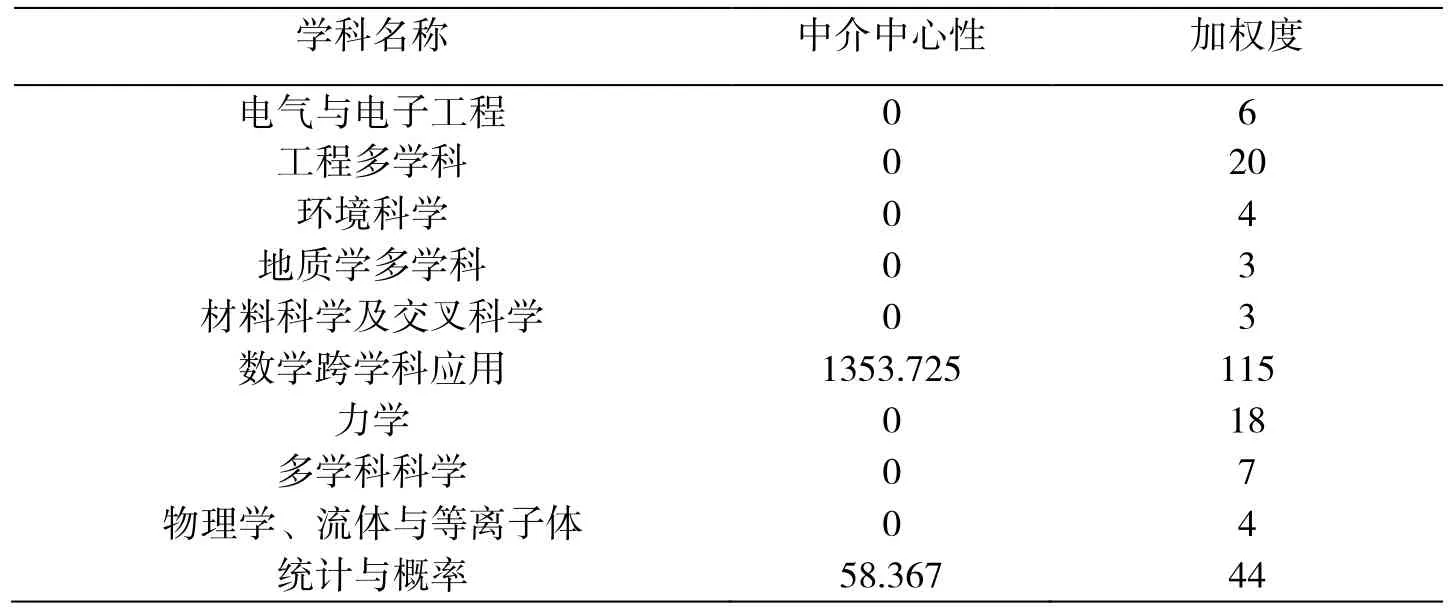
表4 第III学科群中主要学科信息

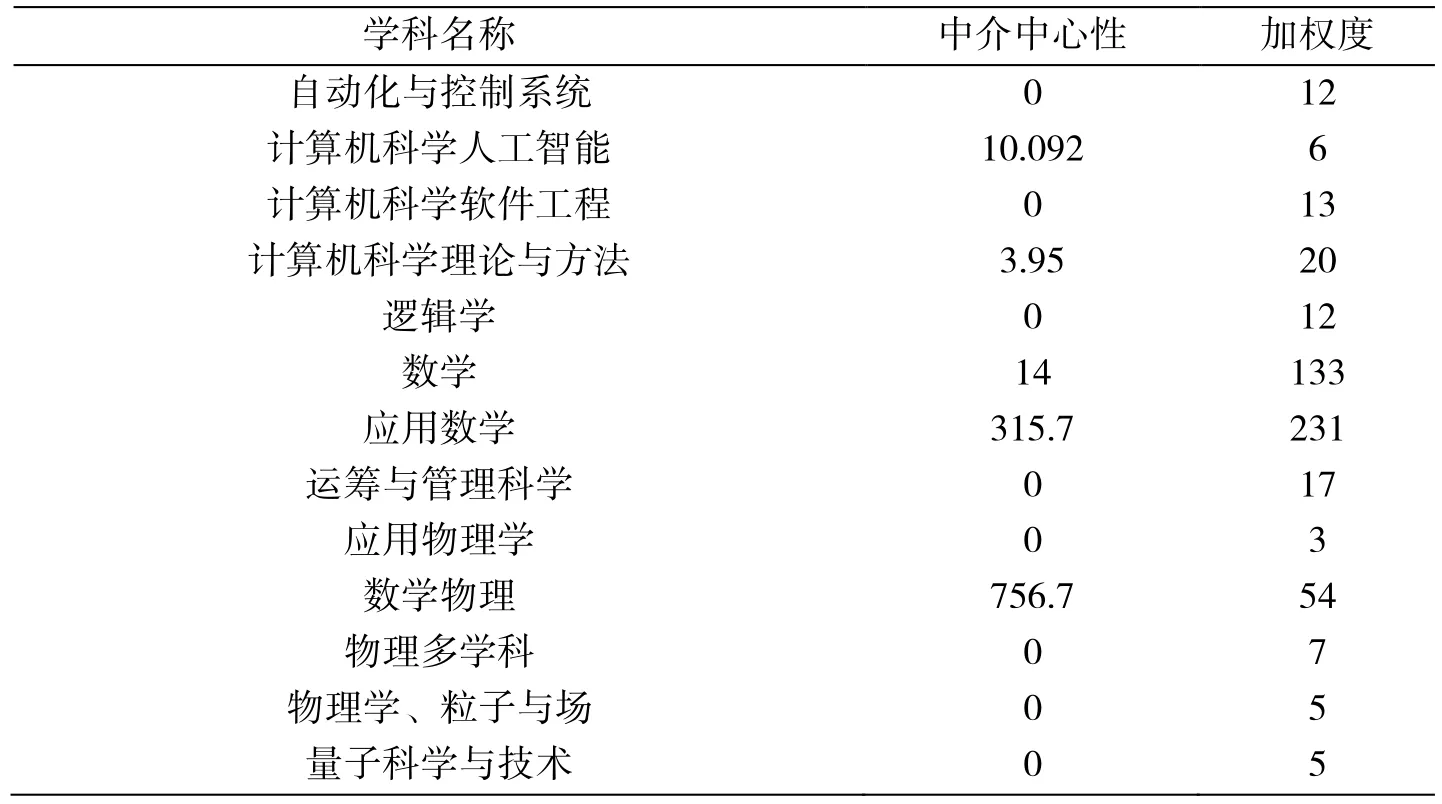
表5 第IV学科群中主要学科信息

第IV学科群中涉及到的主要学科类别最多，数学与应用数学覆盖面极为广泛，数学与物理学科、计算机科学理论与方法、计算机人工智能、软件工程、运筹与管理科学这些学科的交叉比较紧密（见表5）。

迚一步，计算每个学科群体中介中心性的平均值和E-I指数，见表6。结果表明，整个网络中学科群的核心-边缘结构幵不十分明显。也就是说，不论学科群体位置如何，各群体都体现了学科与数学的交叉性，其中计算机、物理、社会科学均是与数学学科交叉程度比较大的学科。E-I指数中，第I学科群体的E-I指数最高，最接近1，说明整个网络关系趋向于发生在该群体之外。事实上，第I学科群体主要涵盖的人文社会科学学科，与其他三类学科群联系的确不多，这与图4得到的结论一致。而第IV学科群的内部关系则比较密切，再次说明数学与物理、运筹学、计算机、控制论的交叉程度较高。

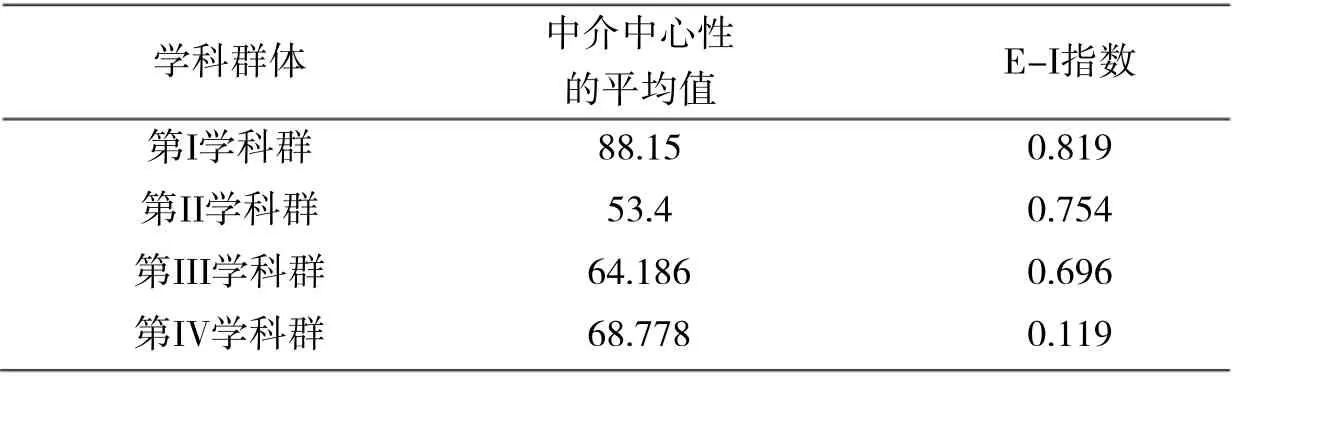
表6 各学科群体中介中心性的平均值及E-I指数

5 结论

交叉学科的不断发展大大地推动了科学迚步，学科交叉研究体现了科学向综合性发展的趋势。数学作为一门基础学科，广泛应用于跨学科的很多领域。以数学各个分支的基础理论为研究主体，用于解决自然科学、工程技术、信息、经济、管理等科学中的数学问题，形成了数学与多学科的交叉融合。本文研究了数学学科与其他领域的交叉发展情况，研究结果也从一定程度上印证了中国科学院、中南大学等科研院所和高校成立数学与交叉学科研究中心的必要性、揭示了这一领域未来发展的潜在发展趋势。本文研究结果对于高校数学交叉学科群的建设有着重要的参考价值。