在线测量不确定度评估及质量控制应用
2021-03-03严宇波黄琳
严宇波 黄琳
(上汽通用五菱汽车股份有限公司,柳州5 450007)
1 前言
在汽车发动机生产过程中,过程受控是质量控制管理主要目标之一,质量控制的基础是来源于可靠的测量数据和合理的控制标准,因此高效稳定的测量系统是真实有效数据的重要保证。测量系统需要满足测量精度高、快速响应、可靠性良好等特点,这其中在线测量在过程控制得到大量的应用。另一方面工艺规范和统计过程控制(SPC)的应用为过程质量控制提供了标准依据,在测量数据的基础上进行控制从而实现零缺陷。测量误差的客观存在无可避免地影响对过程的评估和控制,因此在测量系统选型时就必须先考虑是否能满足规范标准的要求,而且在实际的过程中对于测量误差的忽视将会导致误判和漏判。为避免潜在的质量风险,利用不确定度理论评估测量误差,即能评估测量系统能力是否满足要求,也可进而在实施质量控制时考虑测量误差,有助于提高完善现场质量管理[1-3]。
2 在线测量及其测量原理
广义的在线测量包含刀具监控、加工反馈补偿/闭环控制、质量门等诸多功能,按其应用形式可以分为2 种类型,一是与生产设备集成一体,实时监测加工过程的在机测量系统;另一种则作为生产线一部分工序/独立设备的在线测量机。
曲轴是发动机输出动力的核心部件,因此对几何尺寸和物理性能都有很高的要求,为此在曲轴过程控制除了过程抽检、在机检测还包含终检机作为曲轴最终检测的在线测量设备,实现对曲轴全尺寸测量识别零件质量状态,避免将缺陷零件流出。以某发动机工厂应用的马波斯曲轴终检机为例,其主要结构包括检测工位、测量数据处理系统、控制操作面板、逻辑控制与电箱、气动润滑系统等主要部分组成,测量的核心部分是检测工位和测量数据处理系统。如图1 所示,测量曲轴和使用校准件校零都在测量站单元完成测量动作,曲轴进入曲轴终检机由检测工位工件往复单元将曲轴上料装载到测量站单元定位测量,使用校准件校零时由校准件往复单元就位到测量站单元校准测量机。在测量站单元中曲轴主轴颈(或连杆颈)都采用卡规测量,轴向尺寸采用轴向方向的电子传感器接触测量。曲轴和校准件共用的定心部件设有传感器感应定位状态,实现测量和校准定位基准的稳定性和一致性。测量数据处理系统中测量传感器采集的数据经过数据采集系统滤波放大后,工控机测量软件按程序设定处理并输出测量结果。
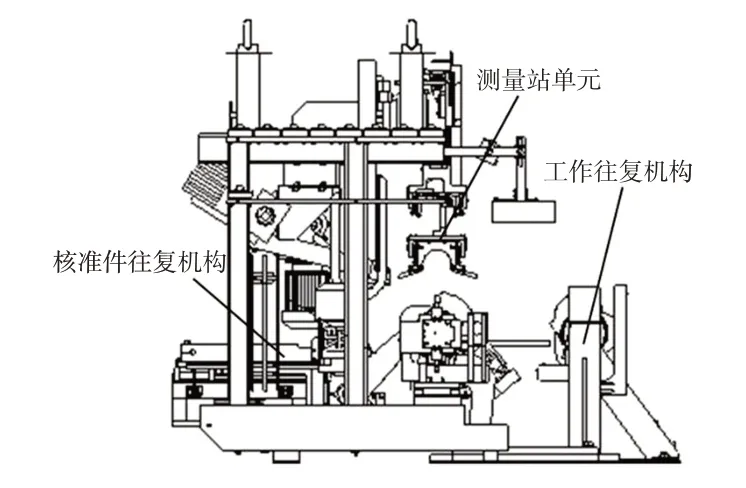
图1 检测工位结构
曲轴终检机的测量特征包含各轴颈直径圆度跳动,轴向距离等几何尺寸,每个特征由1 组传感器采集数据。传感器分布如图2 所示。如轴颈直径和轴向长度等尺寸不涉及基准,由固定在测量单元上的卡规测量,卡规的卡爪两端过轴颈中心布置电子传感器采集数据。卡规校准时使用校准件静态测量,但与校准不同的是测量时工件旋转动态测量。卡规在随动机构随工件运动采集周向数据然后测量数据处理系统的测量程序输出结果。任意轴颈ΦD的测量算法如下。
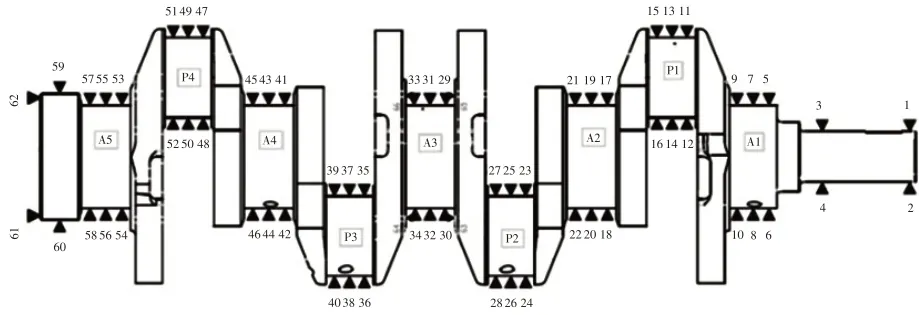
图2 传感器分布
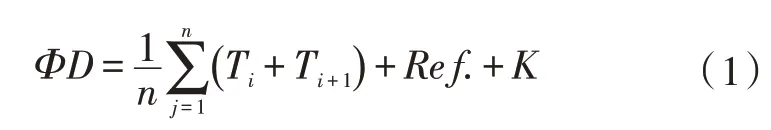
式中,Ti和Ti+1为任意轴颈截面的传感器组;n为工件周向测量采集数据量;Ref.为校准值;K为温度补偿。
形位尺寸根据公差尺寸定义在传感器读数基础上采用不同的算法获得,测量基准两端中心采用定心传感器获取基准定位偏差。形状公差尺寸比如单一截面圆度算法则是该截面卡规传感器读数差的二分之一;平行等位置公差尺寸测量由于基准的影响,在形状误差尺寸和长度尺寸测量基础之外还要补偿基准的偏差。因此对于长度尺寸和形位尺寸测量误差的分析基础都是对应截面卡规测量误差分析。
3 在线测量误差分析
3.1 测量误差分析&建立数学模型
终检机测量曲轴的全尺寸,所有特征都基于对应轴颈测量数据,因此以轴颈直径测量不确定度评估可以代表曲轴终检机的基本情况。而且轴颈直径属于曲轴的关键参数,因此对轴颈直径进行终检机的测量误差分析更具有代表意义。
根据测量原理和程序算法,轴颈的测量误差来源包含以下内容。
a.终检机测量重复性带来的误差μ1;
b.终检机校准件静态定标引入的测量误差μ2;
c.卡规传感器的测量精度μ3;
d.轴颈直径长度类尺寸受环境温度影响,需要进行温度测量误差补偿,引入温度补偿的标准不确定度μ4;
e.终检机校准件校准误差μ5。
根据GUM 评估法需要这些测量误差的标准不确定度[4-5],其中终检机测量重复性带来的误差μ1和终检机校准件静态定标引入的测量误差μ2需要经过统计试验属于A 类标准不确定度,其他属于B类标准不确定度。
3.2 A类标准不确定度评定
a.评估终检机测量重复性的标准不确定度,采用同一曲轴进行重复测量,结果见表1。
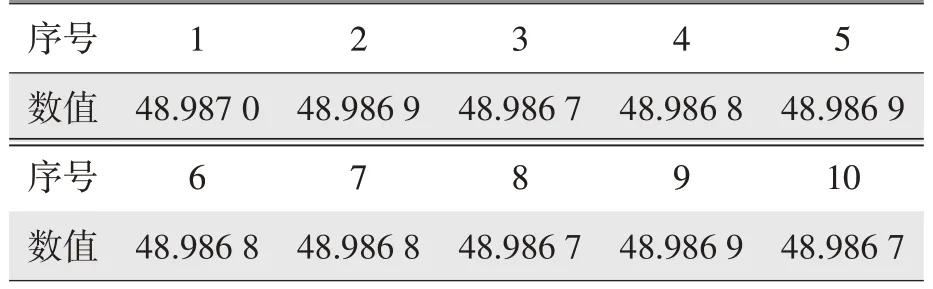
表1 终检机测量重复性 mm
利用贝塞尔公式求得终检机测量重复性引入的标准不确定度μ1=0.031 μm。
b.评估终检机重复定标的标准测量不确定度,跟踪十次定标校零结果与校准值偏差量见表2。
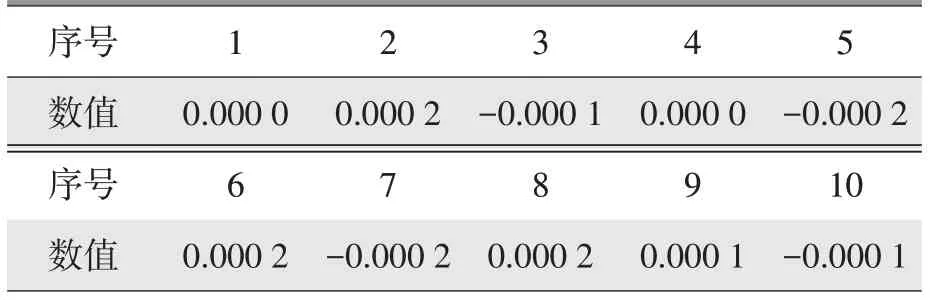
表2 终检机定标重复性 mm
同理可得终检机重复定标的标准测量不确定度μ2≈0.048 μm。
3.3 B类标准不确定度评定
a.传感器的标准不确定度,查传感器技术资料测量线性为0.15 μm,服从均匀分布包含因子,传感器引入的标准不确定度为μ3=0.104 μm。
b.曲轴温度线性补偿系数受温度和材料膨胀系数的影响[6]。设D为轴颈直径,温度线性补偿公式。
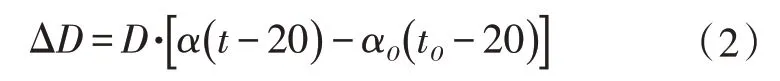
式中,ΔD为温度引起的轴颈直径的变化量;α和αO分别为曲轴和校准件热膨胀系数;t为曲轴温度;o为校准件的温度。
温度线性补偿的标准不确定度由这些参数的误差构成,计算如下。

式中,查资料α=10×10-6mm/℃,曲轴热膨胀系数的误差α=1×10-6mm/℃,αO=11×10-6mm/℃,校准件热膨胀系数的误差αO=1×10-6mm/℃;现场测量曲轴温度t=30 ℃,校准件的温度tO=26 ℃;Δt和ΔtO为温度测量误差取决于温度传感器,查终检机技术资料Δt=ΔtO=0.1 ℃。
因此曲轴终检机温度线性补偿误差标准不确定度μ4=UD=0.576 μm。
c.查终检机校准件校准证书得校准件校准引入的不确定度U=1.2 μm,包含因子取k=2,则校准件校准的标准不确定度μ5=0.6 μm。
3.4 扩展不确定度计算
计算扩展不确定度需要先求出合成标准不确定度,根据前文测量模型曲轴终检机的合成标准不确定度uC计算如下。
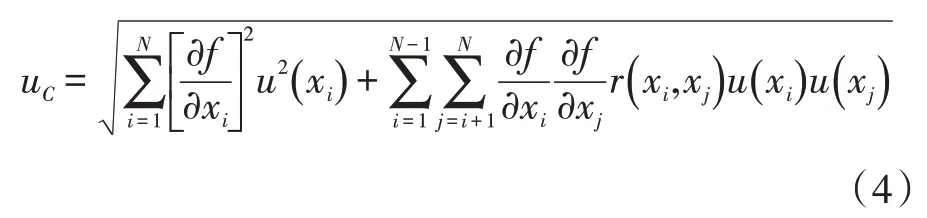
式中,u(xi)为各测量误差引起的标准不确定度分量;为各类测量误差的灵敏系数;r(xi,xj)为测量误差分量xi和xj之间的相关系数。
不确定度各输入量不相关相关系数为零,则计算如下。
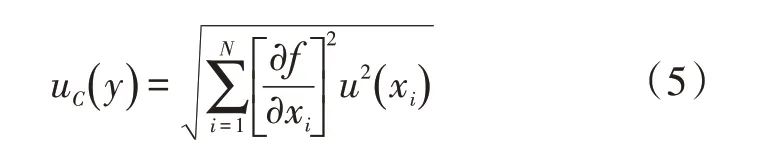
由测量模型可知灵敏系数均为1,则计算如下。
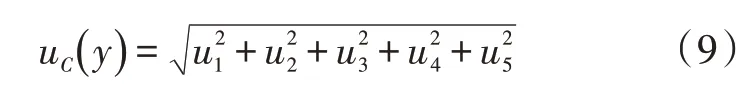
主要标准不确定度分量汇总见表3。
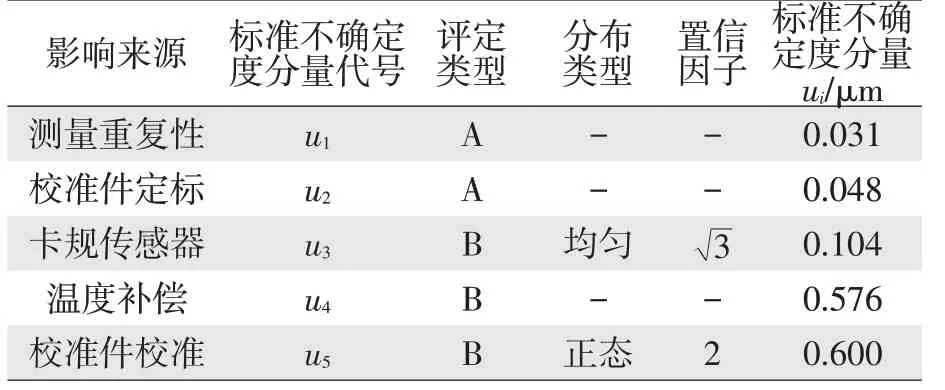
表3 主要标准不确定度分量
则合成标准不确定度计算如下。
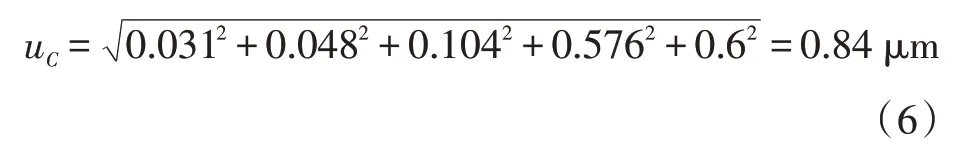
扩展不确定度计算包含因子k=2,则扩展不确定度U=kUc=2×0.84=1.68 μm。
4 考虑测量不确定度的质量控制应用
评估终检机测量不确定度的目的在于指导质量控制。应用GB/T 18779.1—2002《产品几何量技术规范(GPS)工件与测量设备的测量检验[1]第1 部分:按规范检验合格或不合格的判定规则》考虑测量不确定度条件下检验工件的合格或不合格的判定规则,引入不确定区从而使不确定应用于工件质量控制。
如图3 所示,以双边公差尺寸为例,以上限(USL)和下限(LSL)为界限。当工件测量判定不考虑测量误差时,处于C线按设计/工艺规范分为规范内区1,规范外区2。当工件测量判定要考虑测量误差条件时按D线是检验判定,分为合格区3,不合格区4,不确定区5,范围随测量不确定而改变。
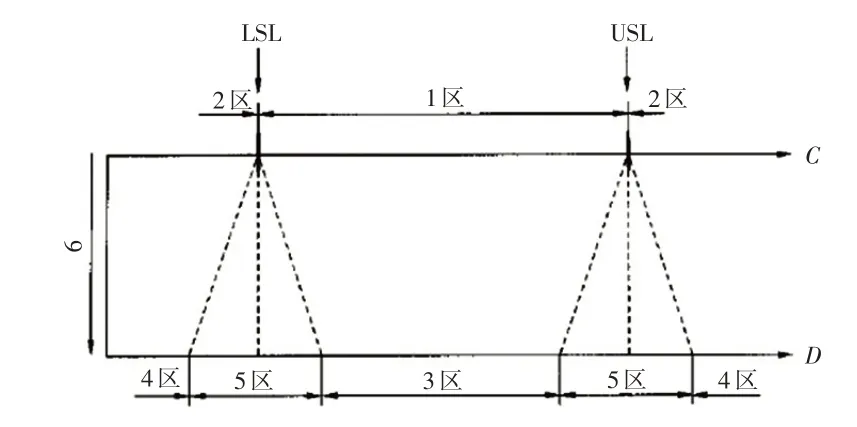
图3 双边公差
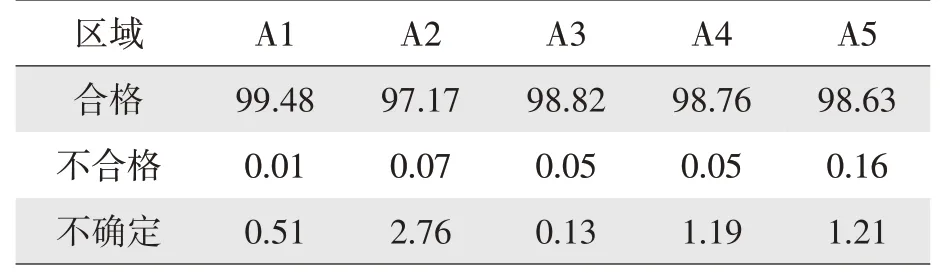
测量误差用扩展不确定度(U)表示:U=kUc,在考虑测量误差条件时测量结果y'=y±U,表示当扩展不确定度为U时,测量结果真值(y)在给定置信概率下的分布区间为(y')范围内,不确定区则是指设计/工艺规范限两侧宽度为测量不确定度的区域,不确定区宽度为2U。当测量示值(y')处于LSL+U 收集曲轴终检机过程100%检测所统计测量数据见表4,应用上述判定规则分析主轴颈直径数据。 表4 主轴颈直径过程检测数据 主轴颈直径尺寸规范(Φ48.987±0.008),当扩展不确定度U=1.68 μm 时,在考虑测量误差条件下合格区(48.980 6 表5 主轴颈直径检测数据区间分布 % 比较表4 和表5 的数据中,虽然各轴颈合格率均满足过程能力,引入测量误差之后不合格并未增加但不确定的比例还是很高。A2 轴颈考虑测量误差条件下合格率即处于合格区的比例(97.17%)相对不考虑测量误差条件下合格率(99.62%),存在2.76%不确定。对于处于不确定区的零件出于质量风险考虑,状态可疑的零件无法忽视,需要有关各方找到适合的判定准则或控制策略,不确定区控制策略可以从下列原则出发[7]。 a.从设备选型、设备/传感器精度、测量方法等方面优化测量系统,通过减少测量不确定度,削减不确定区域增大合格区和不合格区,从而减小测量结果落在不确定区的概率。可以从曲轴终检机测量线性模型,直观的分析出不确定度分量中温度补偿的分量比例最大,在平衡节拍前提下减少曲轴、校准件和环境温度差异从而减少温度补偿不确定度量是相当有效的措施。 b.相对于提高过程能力减小曲轴分布宽度,曲轴终检机现有的能力也可以调整轴颈直径趋于中心分布也可以增加更多的安全裕度。 测量不确定度用于评估测量误差分布已经广泛应用于各领域检定校准和检测试验,但在实际生产过程中的应用相对较少。测量数据采用SPC工具进行数据统计分析作为指导过程控制的依据,由于测量误差的存在SPC 评估的结果存在失真。本研究首先分析了曲终检机测量原理,评估曲轴终检机测量轴径直径的测量不确定,结合国标GB/T 18779.1—2002 简要归纳在线测量质量判定方法[1],整理了检验判定规则的要求。拓展现场质量控制的改善提供新方法和思路
5 结束语
