低轨遥感卫星姿态解耦控制设计与仿真

潘立鑫 王胜刚 袁军 王琳琳

(1 北京控制工程研究所， 北京 100094)(2 内蒙古工业大学， 呼和浩特 010080)

随着航天技术的发展，用户对低轨遥感卫星姿态控制精度及机动能力的要求越来越高。对于卫星姿态控制系统而言，滚动、俯仰和偏航通道之间的交叉耦合，使姿态控制系统成为一个非线性强耦合的复杂多变量系统。针对低轨遥感卫星运动的非线性强耦合特性，人们应用如动态逆[1-2]、神经网络[3-4]、滑模变结构[5-6]、鲁棒控制[7-8]等解耦方法设计了卫星姿态控制系统，并取得了一定的成果，但由于未考虑执行机构特性，物理意义不明确，应用仍相对较少。

解耦控制方法是解决非线性强耦合多变量系统控制设计的一种有效方法。针对低轨遥感卫星动力学模型中存在滚动、俯仰和偏航通道之间的耦合关系，利用解耦控制方法，通过选取解耦控制向量能够将系统动力学模型转换为3个通道彼此独立的子系统模型。以等效的子系统模型作为研究对象，针对3个通道分别设计姿态控制律，可有效解决耦合影响引起的卫星姿态难于控制的问题，能进一步提升优化控制性能指标。

本文采用经典的状态反馈解耦设计[9-10]，依据低轨遥感卫星姿态解耦控制设计原理，通过动量轮转速调节产生控制力矩，实现卫星3轴姿态稳定对地飞行或偏置飞行。在卫星正常对地飞行时，动量轮均运行在偏置标称转速，构成整星零动量。在卫星进行滚动侧摆(或偏航定标)时，动量轮转速偏离标称转速，进而通过动量轮角动量变化产生卫星机动控制力矩。由于该设计在系统结构上将卫星运动耦合模型分解为滚动、俯仰和偏航3个子系统分别进行分析，因此能降低控制器设计的难度，解耦后可独立设计比例积分微分(PID)控制器；另外，在进行解耦控制参数设计时，可以充分借鉴和引用成熟的PID参数整定方法，从而实现卫星姿态控制的快速稳定调节。

1 低轨遥感卫星姿态解耦控制设计

本文姿态解耦设计的总体思路为：首先，在卫星动力学耦合模型的基础上，依据状态反馈解耦控制原理，通过设计解耦控制律，将动力学耦合模型等效转换为滚动、俯仰、偏航3个独立的子系统模型；然后，针对子系统模型，分别设计各通道回路的PID控制器，并从频域指标的角度提出控制参数的选取方法。

1.1 卫星动力学模型

对于低轨遥感卫星，若姿态控制系统的带宽设计合理，则太阳翼挠性振动将在自身阻尼作用下被动抑制。因此，忽略挠性因素，考虑如下简化的动力学模型[11]。

(1)

式中：X，Y，Z为卫星本体坐标系的坐标轴；IX，IY，IZ为卫星3轴的转动惯量；ωX，ωY，ωZ为卫星3轴的惯性角速度；hX，hY，hZ为飞轮在卫星本体坐标系下的角动量；ud,X，ud,Y，ud,Z为外干扰力矩ud在卫星本体坐标系下的分量。

1.2 卫星姿态解耦控制律设计

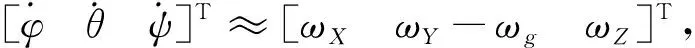
对式(2)线性化，并做拉氏变换，经化简得式(3)。式(3)中：s为拉氏变换的复频率变量；φ(0)，θ(0)，ψ(0)分别为滚动、俯仰和偏航的初始姿态角；等号左端第3项反映了初始姿态角对姿态输出的影响。

根据式(3)的耦合结构，取解耦控制向量，得到式(4)。式(4)中：aφ，bφ，cφ，aθ，bθ，cθ，aψ，bψ，cψ分别为根据响应性能指标选定的参数。

将式(4)代入式(3)，整理得式(5)。式(5)给出了卫星姿态动力学模型在解耦后各单回路的误差传递函数。通过误差传递函数表达式，可以等效设计各单回路的PID控制器，进而满足各项姿态控制指标的要求。

(2)

(3)

(4)

(5)

1.3 基于频域分析的控制参数选取方法

式(4)等号右端第2个矩阵主对角线上的元素构成体现了PID控制设计的思想。要确定式(4)中未知的控制参数，本质上就是对解耦后的单回路PID控制参数进行整定。通常，可首先设计比例微分(PD)控制参数，然后考虑加入积分控制提高系统的稳态精度。下面以滚动回路为例，从系统带宽设计进行分析，从而总结出控制参数定量选取时需满足的约束关系。

1.3.1 PD控制参数的选取

在系统稳定的前提下，将卫星外部干扰力矩作为系统的输入，通过合理设计系统的带宽实现对太阳翼挠性等外部干扰的抑制。解耦后，滚动回路干扰力矩到姿态输出的简化PD控制框图如图1所示。图1中：ωX为滚动角速度；φr为期望滚动角；Kp,φ为滚动回路比例控制参数；Kd,φ为滚动回路微分控制参数；G(s)为滚动回路前向通路上的开环传递函数。

图1 滚动回路控制框图Fig.1 Control block of roll loop

当控制参数Kp,φ=bφ，Kd,φ=aφ时，图1中系统的闭环传递函数为

(6)

闭环系统的幅频特性为

(7)

式中：M(ω)为幅频值，ω为复频率。

根据系统带宽ωb的定义，有

(8)

即

(9)

将式(9)代入式(7)，整理得到系统带宽与控制参数关系为

(10)

当给定期望控制系统带宽ωb后，可根据式(10)确定控制参数Kp,φ与Kd,φ的约束关系，根据系统的设计需求得到各回路PD控制参数的可选域。

1.3.2 积分控制参数的选取

PD控制参数选定后，稳态控制中可引入积分器消除稳态误差，进而提高控制精度，给定积分控制参数Ki,φ的选取规则如下。①在姿态偏差较大(如姿态机动)时不使用积分项，以保证快速性；②在稳态控制时引入积分，以补偿常值干扰力矩，提高稳态精度；③积分项输出进行限幅；④姿态角偏差符号改变时对积分器复位。

2 仿真分析

以资源一号02D卫星为研究对象，进行姿态解耦控制的仿真与分析。资源一号02D卫星采用降交点地方时10:30am的太阳同步回归轨道，轨道倾角98.505 5°，轨道平均高度778.099 km，卫星在轨寿命5年。相比于同类近地遥感卫星[12]，资源一号02D卫星在姿态指向精度和姿态控制稳定度指标方面都具有更高的要求。其控制分系统主要性能指标分别为：3轴姿态指向精度优于0.03°(3σ)；3轴姿态控制稳定度优于5×10-4(°)/s(3σ)。卫星转动惯量为diag(2080,2045,3007)(kg·m2)，飞轮最大力矩为0.13 N·m。

考虑对卫星外部干扰的抑制，取滚动回路的系统带宽为0.01 Hz。根据式(10)，选取Kp,φ=bφ=15，Kd,φ=aφ=1500，同时给定积分参数Ki,φ=cφ=1。采取同样的方法，选取俯仰回路参数bθ=13.5，aθ=1350，cθ=0.5，选取偏航回路参数bψ=20.2，aψ=2020，cψ=0.4，设定积分器的限幅为0.02。

图2和图3分别为资源一号02D卫星在正常模式星敏感器定姿下的姿态角和姿态角速度仿真曲线(卫星引入了偏流角计算)，左侧主坐标纵轴表示滚动、俯仰姿态，右侧次坐标纵轴表示偏航姿态。

从图2和图3可知：资源一号02D卫星姿态指向精度优于0.002°(3σ)，姿态控制稳定度优于1×10-4(°)/s(3σ)，外部干扰对卫星姿态的影响得到了有效抑制。从以上仿真数据分析可以看出：控制分系统性能指标优于设计指标，本文提出的卫星姿态解耦控制设计有效。

图4和图5分别为资源一号02D卫星在正常模式星敏感器定姿下的姿态角和姿态角速度在轨数据曲线(卫星引入了偏流角计算)，左侧主坐标纵轴表示滚动、俯仰姿态，右侧次坐标纵轴表示偏航姿态。

图2 正常飞行姿态角仿真曲线Fig.2 Simulation curves of attitude angles in normal flight

图3 正常飞行姿态角速度仿真曲线Fig.3 Simulation curves of attitude angular velocities in normal flight

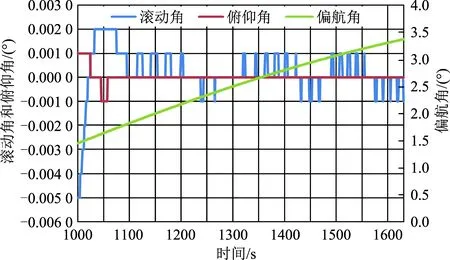
图4 正常飞行姿态角在轨曲线Fig.4 On-orbit curves of attitude angles in normal flight

图5 正常飞行姿态角速度在轨曲线Fig.5 On-orbit curves of attitude angular velocities in normal flight

从图4和图5可知，资源一号02D卫星在轨实现的姿态控制性能指标分别为：姿态指向精度优于0.005°(3σ)，姿态控制稳定度优于4×10-4(°)/s(3σ)。将图4和图2，图5和图3进行比较，可以看出：本文提出的姿态解耦控制设计在姿态指向精度和姿态控制稳定度方面，均优于卫星在轨使用的姿态解耦控制设计。如果能够通过合理设计系统带宽、有效抑制太阳翼挠性振动对卫星姿态的影响，那么应用本文设计可以使卫星姿态控制性能指标得到进一步提升和优化。

3 结束语

本文在低轨遥感卫星姿态动力学模型的基础上，运用解耦控制设计了姿态控制律，并从频域分析的角度研究了姿态控制规律中控制参数的选取。由于设计合理的系统带宽既可以隔离卫星姿态外部干扰，又能加快系统的响应速度，因此本文给出了确定期望系统带宽后控制参数的选取依据，从而可以非常直观地设计控制器来处理不同姿态控制任务。本文以资源一号02D卫星为研究对象，通过对提出的姿态解耦控制设计进行仿真，验证了其可行性和有效性。另外，对仿真数据和资源一号02D卫星在轨数据进行比较，结果表明本文设计能够进一步提升、优化卫星姿态控制性能指标，对于低轨遥感卫星姿态控制系统设计具有一定的参考价值。