尿素溶液制备冰浆的流动特性研究

张盛世 赵彦杰 李兆宁

(1 天津大学中低温热能高效利用教育部重点实验室 天津 300350； 2 天津大学机械工程学院 天津 300350)

冰浆是指某类盐溶液和冰晶粒子的共晶混合物，是一种呈泥浆状的悬浮液。它具有良好的流动特性和较高的能量密度，既可作为相变冷库材料，又可作为第二制冷剂来输送冷能。在空调系统、食品加工、冷藏运输、医药等领域应用广泛[1]。

冰浆通常由盐溶液而非纯水制取产生。溶液中溶质的不同可以改变冰点温度，降低结冰附着力并减小冰的粒径。低浓度溶液的凝固点降低规律遵循溶液的“依数性”原则。溶液在冻结过程中溶质发生迁移，因此在固液两相区，可以观测到固相区中包含大量的小冰粒[2]，而且溶液中溶质的化学键具有阻止冰晶生长的作用[3]。所以冰层附着力低，生成的冰浆更加均匀，抑制了冰堵的发生和换热的恶化。溶液中常见的溶质主要有氯化钠、乙醇、乙二醇和丙二醇等。

在设计热能存储系统之前，首先应重点了解冰浆的流动特性。冰浆作为固液两相流体，流动特性复杂，受多种因素影响，包括溶质变化、溶液浓度、流速、管道尺寸和含冰率(ice packing factor, IPF)等。国内外对冰浆的研究已有20多年的历史，其中冰浆的流动特性已得到了广泛的研究和应用。Tian Qiqi等[4]提出了3种管内冰浆的流动模式：悬浮流、移动床流和固定床流。悬浮流在高流动速率下发生，冰粒完全悬浮并均匀分布。移动床流在较低的流动速率下发生，流动过程中浆体被分为两层，顶层为移动床层，而底层仍然是非均质流层。固定床流则在非常低的流动速率下发生，在该流动模式下，载流体因无法承载所有的移动床层而在管道顶部形成了固定床层。V. Ayel等[5]回顾了4种流变模型，即Bingham模型、 Casson模型、 Ostwald模型 和 Herschel Buckley模型，这些模型有助于预测不同条件下管中冰浆的流动行为。H. Kumano等[6]主要研究了乙醇溶液制取冰浆的流动特性，并建立了管道摩擦阻力系数与雷诺数之间的关系，文中指出，在层流条件下，可以将冰浆看做假塑性流体进行处理。H. Kumano等[7]分析了初始溶液浓度对冰浆流动特性的影响，结果表明，利用初始质量分数为5%和10%的乙醇溶液制取的冰浆，其流动特性同假塑性流体的流动特性相近，而由质量分数为2%的乙醇溶液制取冰浆则可看做牛顿流体。B. D. Knodel等[8]研究了乙二醇溶液制取冰浆的流动特性，通过实验测量了冰浆流动过程中的再分层特性，指出冰浆流动过程中的摩擦压降随着含冰率的增加而降低。刘巨保等[9]研究了氯化钠溶液制取的冰浆在水平管中的流动特性，基于两相流和颗粒动力学理论，分别研究了管径、管长、IPF、流速对冰浆流动过程中压力损失的影响。

然而到目前为止，研究人员所选取的制取冰浆的溶液及实验环境各不相同，因此对于冰浆流动特性的研究还未达成统一的共识。本课题组之前的研究[10]指出，尿素溶液的相变潜热均高于同浓度的常规制备冰浆的溶液，如乙醇溶液和氯化钠溶液。质量分数为10%的尿素溶液的相变潜热高达311.2 J/g，略低于纯水的潜热，而且尿素溶液的相变潜热随着浓度的降低愈发接近于纯水的潜热。同时尿素溶液完全冻结后形成的冰层质地松软，具有多孔结构，极易被液流的剪切力剥落，可以自发产生冰浆，并且目前还未发现有研究学者对尿素溶液制取冰浆的流动特性进行研究。因此，本文以尿素溶液所制取的冰浆作为研究对象，测量了不同初始质量浓度尿素溶液在常温状态和冰水混合物状态的运动黏度，观测了冰浆中冰粒分布情况及大小，分析了管径、 IPF和流速对摩擦阻力系数的影响，并根据实验结果阐明了冰浆在水平管中的流动特性。

1 实验装置及方法

1.1 实验装置

冰浆的高效制备和冰浆在水平管内的流动特性对于指导蓄冷系统的设计至关重要，为此我们沿用本课题组之前设计的冰浆制备和流动特性测试实验台[11]，实验装置如图1所示。实验系统主要包括3部分：冷却液循环回路、冰浆制备循环回路和冰浆的流动特性实验测试段。图中虚线箭头所示为冷却液循环回路。恒温箱为系统制备冰浆提供冷量，恒温箱的最大制冷量为7.8 kW。恒温箱中的冷却液采用体积比为1∶1的乙二醇溶液，最大冷却温度可达 -33 ℃。在整个循环过程中，乙二醇溶液作为携带冷量的冷却液，流经制浆罐的夹层，并将冷量转移至罐中的尿素溶液中。

图1 实验装置

在冰浆制备循环回路中，通过过冷法在制浆罐中制备冰浆。制浆罐设计为套筒式，内筒盛有质量分数为5%的尿素溶液，容器的容积为10 L；外筒循环流动乙二醇冷却液，采用左右并进、下进上出的模式，以起到强化换热的效果，并通过调节来自恒温箱的乙二醇冷却液温度来控制制浆罐中温度。同时在制浆罐内筒中安装一个电动搅拌器，用于打破尿素溶液的过冷状态并除去冰浆中的空气。搅拌器的转速范围为0～300 r/min。搅拌罐顶部布置一个有机玻璃顶盖，顶盖上有两个小孔，用于插入两根T型热电偶，以测量制备过程中溶液和冰浆的温度变化，热电偶的精度为0.001 ℃。系统中封闭的实线箭头回路为溶液和冰浆的循环回路，整个循环管道均为DN15的不锈钢直管和软管，循环的动力装置为带有逆变器的小型离心泵，额定功率为370 W，扬程范围为7.5～11.6 m，体积流量范围为1.2～6 m3/h。通过对离心泵进行频率转换来控制流量。系统中采用Coriolis 质量流量计测量和记录溶液和冰浆的质量流量和密度变化，流量测量量程为0～3 000 kg/h，测量精度为0.1%；密度测量范围为0.3～3.000 g/cm3，测量精度为±0.002 g/cm3。流动速率用于计算冰浆流动过程中的雷诺数Re，冰浆的密度用于计算IPF。离心泵工作过程中内部产生的热量对冰浆中IPF的降低无法避免也不能被忽略，所以将Coriolis质量流量计安装在离心泵的出口处，以提高质量流量和密度数据的可信度。冰浆的温度测量范围为-200～350 ℃，测量精度为±0.01 ℃，工作压力为0～4.0 MPa。在冰浆进入测试段之前首先会流经一段长度为1.5 m的充分发展段，以确保进入测试段的冰浆处于稳定状态，减小测量误差。测试段长1.2 m，并在测试段的两端分别布置一个压力传感器，量程为0～0.6 MPa，精度为0.01%，输出信号为4～20 mA，同时在压力传感器后并联一个阻值为1 Ω的电阻，电阻精度为0.02%，用于将电流信号转化成电压信号，因为数据采集器仅接受电压信号。又因4～20 mV电压与0～0.6 MPa的压力数据呈线性关系，所以可通过电压信号线性计算出压力数据，两个压力相减即可得到压降Δp0。在压降测量实验结束后，通过溶液储罐收集冰浆。测试段采用的不锈钢管分为内径4、6、8 mm三种，用于研究不同管径内冰浆的流动特性。由于测试部分的长度有限，在测试过程中IPF的变化很小。此外，实验设备中的制浆罐和所有管道均采用橡胶绝缘棉进行包裹，有效减少热量损失。

1.2 制取冰浆

图2 尿素溶液的过冷度的变化

本文采用循环和机械搅拌的方法制取冰浆，质量分数为5%的尿素溶液在套筒式搅拌罐内被不断地降温和搅拌，并为了防止冰堵和实现冰浆的制备，制取冰浆的过程中溶液在离心泵的作用下一直处于循环流动状态。随着温度的不断降低，溶液在搅拌和流动的作用下迅速接触过冷态，之后冰浆大量生成。随着时间的延续和冷却液温度的降低，冰浆的含冰率会不断增加。本实验主要制备含冰率为5%～30%的冰浆，并研究其流动特性。尿素溶液的过冷度主要受搅拌器转速和冷却速度的影响，如图2所示。在冰浆的制备过程中，首先设定80、120、150 r/min三种不同的搅拌转速，图2(a)所示为制浆罐内壁面温度Tw=-5.2 ℃时，质量分数为5%的尿素溶液在不同搅拌转速下的冰浆的制取过程。可以看出，搅拌转速的提高促进了冰浆的生成，并促进了过冷态的解除，三种转速对应的过冷状态的最低温度分别为-1.74、-1.55、-1.34 ℃。图2(b)所示为搅拌转速为 150 r/min 时，质量分数为5%的尿素溶液在不同壁面冷却温度Tw下冰浆的制取过程，冷却温度的降低促进了冰浆的生成，但抑制了过冷态的解除，随着Tc和Tw的降低，过冷态的最低温度也会略有下降。而且，较低的壁面温度Tw也会使壁面冰层附着加剧，从而会恶化传热，影响冰浆的持续生成。

图3(a)所示为Tw=-8.6 ℃时出现冰浆30 min之后制浆罐内的状态。制浆罐壁面附着了一层致密的冰层，占据了壁和搅拌器叶片之间的空间，传热恶化，不利于冰浆的制备。图3(b)所示为Tw=-4.1 ℃时出现冰浆30 min之后制浆罐内的状态。制浆罐内壁面几乎无冰层附着现象，有利于冰浆的制备。通过实验发现，在质量分数为5%的尿素溶液的冰浆制备过程中，由于搅拌和循环的作用，过冷度很低，仅为1～2 ℃，而且生成的冰浆更加均匀，可以认为利用盐溶液的搅拌降温制取冰浆是一种良好的制取蓄冷用冰浆的方法。

图3 冰浆照片

冰浆的制备过程持续进行，直至制备出的冰浆满足某一特定含冰率(IPF)的要求。IPF的计算式[6]为：

(1)

图4 冰浆中的冰粒分布

式中：ρs为初始溶液的密度，g/cm3；ρsl为冰浆的密度，g/cm3，两者均通过质量流量计测量获得；ρi为纯冰的密度，取0.9 g/cm3。

图4(a)所示为不同含冰率的冰浆的形态实物图，可以看出冰粒的形态类似于红细胞，利用放大50倍的工业相机对含冰率为0.126、0.181和0.258的冰浆形态分别进行拍摄，并利用像素点测量的方法对冰粒的尺寸进行精确测量，取照片中每一个冰粒的最大尺寸和最小尺寸的平均值进行统计，绘制出冰浆中冰粒直径的频率分布图，如图4(b)所示。由图4(b)可知，三种不同含冰率下冰粒的尺寸多分布在0.10～0.25 mm内，平均尺寸约为0.15 mm。对于不同含冰率的冰浆，冰粒的尺寸无较大区别。

1.3 尿素溶液的性质

随着温度的不断降低，溶液将在其平衡冻结温度下进行冻结，导致残留溶液中溶质浓度提高，使冰和溶液之间的相平衡得以维持。在冰浆的流动特性的研究中，需要测量尿素溶液的各项性能，其中Re是一个非常重要的参数，而在确定Re的过程中，运动黏度是计算Re的关键参数。采用Ubbelohde黏度计对不同初始质量浓度尿素溶液在常温状态和冰水混合物状态的运动黏度进行测量。

图5所示为不同质量浓度尿素溶液在冰点状态的运动黏度关系图。整个实验在过冷状态下进行。随着尿素溶液质量分数由0 %增至32.5 %，冰点温度从0 ℃线性降至-11.5 ℃，冰点状态的运动黏度从1.648 mm2/s增至6.736 mm2/s。通过对比可知，固液两相的流体的运动黏度大于纯液体的运动黏度。图5中的公式为冰点状态运动黏度与温度之间的拟合公式。

1.4 实验条件

实验通过测量不同管径、Re和IPF下的压降来研究水平管中冰浆的流动特性。实验条件如表1所示。

表1 实验条件

2 结果与讨论

2.1 流动压降

冰浆本质上为一种固液两相混合流体，不同含冰率的冰浆流动压降较单相流体更为复杂，对冰浆流动压降的分析是研究其流动特性的基础。图6所示分别为IPF为0.06、0.14和0.24的三种不同管径的流动压降与Re的关系。由图6可知，冰浆的流动压降与IPF呈正相关，压降随IPF的增加而增加，同时也随Re的增加而增加，但随着测试管径的增加，压降逐渐减小。冰浆流动压降对参数的灵敏等级为：管径>IPF>Re。图7所示分别为在内径为6 mm的测试段内，不同IPF的冰浆分别在层流和湍流状态下流动压降与Re的关系。在层流条件下，不同IPF的冰浆，其压降随Re的增加而增大。当从层流过度至湍流的过程中，不同IPF的冰浆压降接近，在湍流条件下，不同IPF的冰浆，其压降继续随Re的增加而增大。同时，对于高IPF的冰浆，湍流的压降增长的速率较大，同时高IPF的流动压降较大。流态决定了冰浆的基本流动特性。在层流和湍流条件下，IPF对高Re状态下的压降影响更为显著。说明Re越大，冰浆的IPF对压降的影响作用越大。

图6 不同管的压降与Re之间的关系

图7 不同IPF冰浆在层流和湍流条件下的压降对比

2.2 摩擦阻力系数

单纯的压降数据分析很难研究不同Re和不同管径内的冰浆与单相流的流动特性之间的差别。而摩擦阻力系数λ是冰浆在管内流动过程中一个非常重要的参数。分析冰浆与纯尿素溶液的管内流动摩擦阻力系数的比值偏离1的程度与IPF和Re的关系，能更加直观地看出作为一种固液两相流体的冰浆与牛顿流体的流动差别，对冰浆蓄冷系统浆体的高效输送和能耗分析具有重要意义。本文研究了冰浆的实验摩擦阻力系数结果与尿素溶液理论值之比，以阐明尿素溶液产生的冰浆的流动特性。

式(2)和式(3)分别为层流和湍流状态下牛顿流体的摩擦阻力系数的理论公式，式中的Re通过式(4)计算得出。冰浆流动过程中管道摩擦阻力系数的实验值λ由式(5)计算。

λlam=64/Re

(2)

λtur=0.316 4Re-1/4

(3)

Re=ud/μf

(4)

λ=2DiΔp/(Lρu2)

(5)

式中：u为冰浆的流速，m/s；Di为测试段管径m；μf为冰浆的运动黏度，mm2/s；Δp为流动压降，Pa；L为测试段管道的长度，m。

图8所示为不同Re条件下，冰浆管内流动摩擦阻力系数的实验值λ与把冰浆作为牛顿流体利用经验公式得到的理论值λ0(λlam、λtur)的比值和IPF的关系。结果表明，在所有条件下，λ/λ0均随IPF的增加而增大，λ/λ0偏离1的程度整体随Re的增加而降低。层流状态(Re=1 500)下，λ/λ0偏离1的程度远大于湍流状态(Re=3 500、6 000、8 500)。以管径为8 mm为例，当Re=1 500且IPF=0.28时，在层流条件下λ/λ0为5.5。当Re=3 500且IPF=0.28时，在湍流条件下λ/λ0为2.2。当然这与λ0在计算过程中使用的经验公式不同有直接关系，但根本原因可用Doron的颗粒流动理论[12]来解释，当冰浆流速较大时，在强湍流状态下，冰晶粒子保持充分的均匀悬浮状态，冰浆接近单相牛顿流体；流速进一步降低，湍流度则降低，冰粒比水轻，故漂浮在管道顶部；随着平均流速继续减小，进入层流区域，冰晶粒子还会在管道顶层形成滑动的沉积物，称为移动层，同时管道最底部形成固定层，冰浆偏离单相牛顿流体。即Re越大，冰晶粒子和溶液混合更均匀；而低流速下，由于分层现象的出现，冰晶粒子多分布在管道的底部和顶部，增加了冰浆中固相与管内壁的摩擦，黏性摩擦阻力相对更大，从而相对高流速、高Re的状态更加偏离单相流。对比三种不同的管径可知，最小管径为4 mm中，不同Re的λ/λ0均小于其他管径的结果。原因是在小管径内，相同Re下，流速较大，冰粒在管内流动时相对大管径内分布更加均匀，分层现象较弱，结合颗粒流动理论，所以小管径内冰浆的流动相对大管径更接近于单相流，故λ/λ0更接近1。

图8 管道摩擦阻力系数与IPF间的关系

2.3 范宁摩擦阻力系数和修正雷诺数

分析摩擦阻力系数比，发现无法将冰浆作为牛顿流体去分析其流动特性，因此，本文将冰浆看做拟塑性流体来分析其流动特性。对于固液两相的非牛顿流体，由于流动剪切应力τw和剪切速率γw之间非线性关系，所以黏度不恒定，而是随着冰浆剪切速率的变化而变化。V. Ayel等[5]综述了Bingham、Casson、Ostwald和Herschel- Buckley四种流变模型，用于预测不同流动状态下非牛顿流体剪切速率和剪切应力之间的非线性关系。本文采用Ostwald模型，即幂律模型来描述冰浆的流动特性：

(6)

式中：τw为剪切应力，MPa；γw为剪切速率，s-1；n′为流动特征指数(无量纲数)，n′=1时为牛顿流体，n′>1时流体剪切增稠，n′<1时流体剪切变稀；K′为稠度系数，mm2/s，依赖于n′和运动黏度[13]。

在水平直管中，流体在管内作层流流动时，其壁面剪切应力τw和剪切速率γw[14]分别如式(7)和式(8)所示：

τw=DiΔp/(4L)

(7)

γw=8u/Di

(8)

流动特征指数n′和稠度系数K′满足本构方程，如式(9)所示：

ln(DiΔp/(4L))=lnK′+n′ln(8u/Di)

(9)

因此通过测量流动时的压降和流速，分别对ln(DiΔp/(4L))和ln(8u/Di)两个数据进行微分拟合即可得到流体的特征指数n′，即式(10)：

(10)

图9所示分别为管径为4、6、8 mm的剪切应力与剪切速率的对数关系。从实验数据的拟合曲线可以明显看出，每条线的斜率是恒定的，说明幂律模型适用于冰浆。由式(10)可知，拟合曲线的斜率即为特征指数n′，截距即为稠度系数K′，分析了IPF分别为0.06、0.10、0.14、0.18、0.22和0.26的不同拟合结果，发现随着IPF的增加，拟合直线的截距逐渐增大，斜率逐渐减小，反映在本构方程(式(9))中，即K′逐渐增大，n′逐渐减小。同时， IPF一定时，随着管径的增加，拟合直线的截距逐渐增大，斜率逐渐减小，即K′随IPF的增大而增大，n′随IPF的增大而减小。图10所示为不同管径的流动特征指数n′、稠度系数K′与IPF的关系。由图10可知，n′随着 IPF的增大而减小，当含冰率为0.06时，冰浆中主要为尿素溶液，此时流动特征指数接近于1，随着IPF的增大，流动特征指数愈发小于1，且随着IPF的增加更加偏离于1，说明低IPF下冰浆近似为牛顿流体，IPF越高，偏离牛顿流体的程度越大，为非牛顿流体，即拟塑性流体。而K′与IPF则呈正相关，IPF为0.06时，K′接近于0，随着IPF的增加，稠度系数逐渐升高，这是因为冰浆中固相颗粒的增加使得流动的阻力变大，导致流体的稠度变大。

图9 剪切应力与剪切速率间的关系

图10 n′、K′和IPF之间的关系

分析不同管径对特征指数n′和稠度系数K′的影响，发现在相同IPF下，随着管径的增大，n′更偏离于1，即管径越大，流体偏离于牛顿流体的程度更大。随着管径的增大，K′也更加偏离于0，基本呈现规律是管径越小，流体的流动粘稠度越低，小管径内偏离牛顿流体的程度越小，这与小管径内流速较大，溶液和冰粒混合更加均匀，流体更加接近单相流有关。分析IPF为0.26的状态下的稠度系数，发现4 mm管径下的稠度系数K′偏离0的程度甚至超过了6 mm管径下的K′。这可能是因为IPF较高的情况下，虽然高流速下溶液和冰晶混合较均匀，但冰浆内冰晶的体积分数较大，且管径较小，固相冰粒对管径的碰撞作用相比于高流速对两相均匀混合的影响更为显著，所以在高含冰率(IPF=0.26)下表现出独特的趋势。

基于已有的冰浆的流动压降数据，利用式(11)可以得到水平细管内冰浆流动的范宁摩擦阻力系数：

fF=λ/4=DiΔp/(2Lρu2)

(11)

通过分析摩擦阻力系数比可知，无法将冰浆作为牛顿流体分析其流动特性，因此，本文将冰浆看做一种固液两相的非牛顿流体进行分析，其流动比单相流更加复杂，单相流体的摩擦阻力来自于黏性摩擦阻力，即流体在壁面附近的黏滞力；而对于包含固相颗粒的两相流体而言，除了黏性摩擦阻力，还存在由固相颗粒同管壁间碰撞产生的运动摩擦阻力，对于额外的运动摩擦阻力，在层流流动状态下的影响还较弱，但当流动状态过渡到湍流状态时，固相颗粒在径向的流动也会增强，使固相颗粒同管壁间的相互作用增加，从而使运动摩擦阻力的影响增强[15]。为了更好地描述非牛顿幂律模型流体的复杂的流动特性，A. B. Metzner等[16]提出了修正雷诺数ReMR代替常规雷诺数Re，ReMR可以利用式(12)求得：

(12)

对于层流流动区域，因层流状态下由冰粒和管壁之间的碰撞引起的运动摩擦阻力影响较小，仍采用牛顿流体的范宁摩擦阻力系数表达式，但在式中利用修正雷诺数ReMR代替常规雷诺数Re。如式(13)所示：

fF=16/ReMR

(13)

在湍流区域，由于冰粒与管壁之间的碰撞而引起的运动摩擦阻力较大而无法忽略，D. W. Dodge等[17]提出了采用充分发展阶段光滑管内的半经验关联式计算摩擦阻力系数，如式(14)所示：

(14)

图11所示为修正雷诺数与常规雷诺数的比值与IPF的关系。由图11可知，比值均小于1，说明修正雷诺数均小于常规雷诺数，这主要是由于冰浆流动时固相黏滞力较大，而且随着IPF的增大，雷诺数的比值更加偏离于1，修正雷诺数更小。尤其在弱湍流区域，如Re=3 500时，ReMR在三种管径中均小于2 300，即越过了过渡区，实际状态已经为层流。该现象可以用层流化[18]的理论来解释，即在一定的流速下，固相质量分数的增加使固-液两相的相互作用增强，更多能量由紊流状态传送到整个流动截面，导致浆体的整体紊流程度下降，弱紊流区域的流动甚至会从紊流流动状态转化为层流状态。

图11 雷诺数比值与IPF的关系

虽然雷诺数比值与IPF的变化呈负相关，但随着常规雷诺数的增加，比值减小的程度逐渐减小，尤其在常规雷诺数Re=8 500时，IPF=0.18、0.22、0.26时的比值只略有减小，基本不变。而在低流速(Re=1 500、3 500)下，雷诺数比值减小的趋势在IPF为0.3以内一直明显，由前文分析可知，这两种常规雷诺数的实际状态其实均已经为层流状态。说明冰浆在强湍流区域流动状态更稳定，而层流和过渡区域的流动特性更为复杂，这主要是因高流速下的冰浆内液相和固相分布更均匀，而低流速下冰粒和溶液的分层现象的出现使流动规律更复杂。

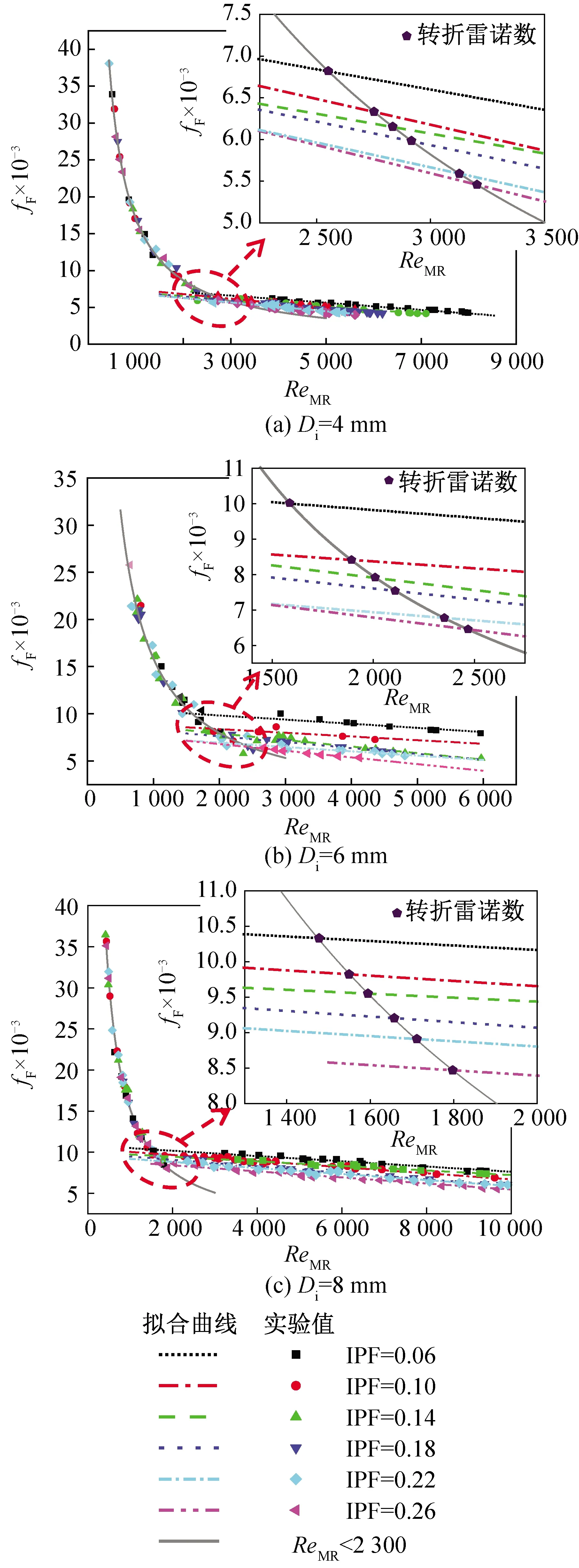
图12 范宁摩擦阻力系数与修正雷诺数间的关系

图12所示为不同IPF的范宁摩擦阻力系数与修正雷诺数之间的关系。图中实线为实验数据的拟合曲线。当ReMR<2 300时，实验值按照反比例函数拟合曲线，拟合公式遵循式(13)；当ReMR>2 300时，实验值按照线性函数拟合曲线，拟合公式遵循式(14)。由图12可知，随着ReMR的增加，fF逐渐减小，这和摩擦阻力系数与常规雷诺数的关系是一致的。观察拟合曲线可知，低雷诺数的曲线拟合和高雷诺数的曲线拟合在不同的IPF下有不同的交点。B. Niezgoda-zelasko等[19]将这种交点对应的修正雷诺数定义为冰浆从层流向紊流转化的转折修正雷诺数。M. Grozdek等[20]提出冰浆的转折雷诺数范围大多为1 700～2 500，而具体的转折雷诺数的数值同冰浆的IPF和管径有关。在本实验中，随着IPF的增加，转折雷诺数的数值随之增大，即会出现处在某一相同的转折雷诺数时，低IPF的冰浆流动处于湍流状态，而高IPF的冰浆流动仍处在过渡区或层流状态。这就是固液两相流体中经常出现的层流化现象，即IPF的增加使固液两相间的相互作用增强，更多能量由湍流核心传送到整个流动截面，导致浆体的整体湍流程度下降，从而弱湍流区域的流动状态其实已经转化为了层流状态。分析不同管径的结果，随着IPF的增加，4 mm管道内的转折雷诺数的范围大约在2 500～3 200；6 mm管道内的转折雷诺数的范围约为1 600～2 500；8 mm管道内的转折雷诺数的范围约为1 500～1 900。所以冰浆的转折雷诺数随着管径的增加而呈现减小的趋势。

由图12还可知，当实验管径为4 mm时，实验值略大于理论分析值，主要是由于较小的管径导致冰浆颗粒与管壁之间的碰撞和摩擦更为严重。当管径为8 mm且ReMR在2 000～3 500之间时，实验值大于理论分析值。因为此时冰浆流处于层流到湍流的过渡区域，并且充分发展的程度很低，而计算模拟值的半经验公式是通过大量充分发展的流动状态数据获取的，因此此处的误差较大。

3 结论

本文以质量分数为5%尿素溶液所制取的冰浆为研究对象，通过测量冰浆的运动黏度及冰粒尺寸，观测冰浆中冰粒分布情况，研究冰浆制备及不同含冰率、不同雷诺数和不同管道内的流动特性，得到如下结论：

1)冰浆中冰粒的尺寸多分布在0.1～0.25 mm之间，平均尺寸约为0.15 mm，冰粒的平均尺寸与IPF之间无明显关联。

2)冰浆的压降随IPF或Re的增加而增大。随管径的增大而减小。冰浆流动压降对参数的灵敏等级为：管径>IPF>Re。对于高含冰率的冰浆，湍流状态下压降增长速率较大。流态决定了冰浆的基本流动特性。在层流和湍流条件下，IPF对高雷诺数状态下的压降影响更为显著。

3)分析流动摩擦阻力系数的实验值与利用牛顿流体的经验公式求得的理论摩擦阻力系数的比值，发现偏离1的程度整体随着雷诺数的增加而降低，在层流区域的比值较大，且远大于湍流状态。在小管径内，由于流速较大，冰浆中固液两相混合更加均匀，从而摩擦阻力系数的偏离理论值越小，即更接近于单相牛顿流体。

4)经过分析摩擦阻力系数比，发现无法将冰浆看作牛顿流体，将其看做非牛顿流体，利用幂律模型分析其流动特性。结果显示，冰浆的流动随着IPF的增加而愈发偏离牛顿流体。流动特征指数n′随着IPF的增大而降低，IPF的增加使冰浆更加偏离牛顿流体。而稠度系数K′和IPF的增长呈正相关，当高含冰率(IPF>20%)时，K′的变化更加显著。此外，当含冰率介于5%～30%范围内，n′随着管径的增大略微减小，K′随着管径的增大而逐渐增大。

5)通过分析修正雷诺数和范宁摩擦阻力系数的关系可知，随着IPF的增加，4 mm、6 mm和8 mm管道内的转折修正雷诺数的范围分别为2 500～3 200、1 600～2 300和1 500～1 900。所以冰浆的转折修正雷诺数随着管径的增加而呈现减小的趋势。