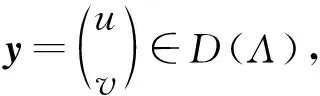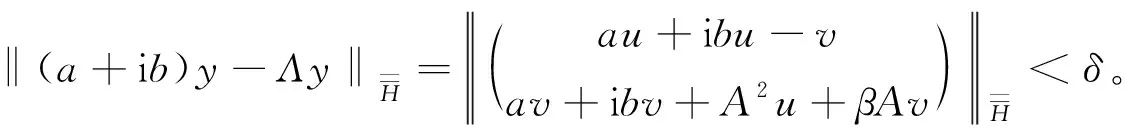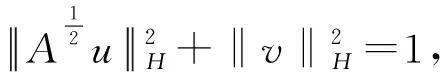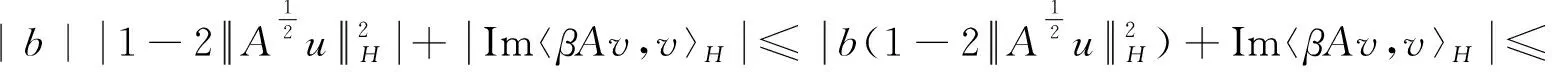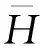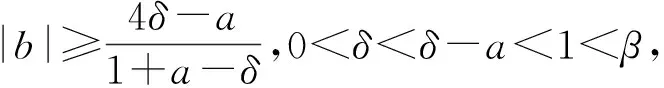Hilbert空间中具有结构阻尼的弹性系统的渐近稳定性

王倩倩

(兰州交通大学 数理学院， 甘肃 兰州 730070)

机械振动所研究的对象是机械或结构，在理论分析中要将实际的机械或结构抽象为力学模型，即形成一个力学系统。可以产生机械振动的力学系统，称为振动系统，简称系统。实际的振动系统，都具有连续分布的质量与弹性，因此，称之为弹性系统。由于确定弹性体上无数质点的位置需要无限多个坐标，因此弹性体是具有无限多自由度的系统，它的振动规律要用时间和空间坐标的函数来描述，其运动方程是偏微分方程。

结构的振动和稳定性研究，是结构力学和数学领域内的热点之一，这不仅是因为它具有较高的理论价值，而且还有着广阔的应用背景。例如，振动改进和控制在维持高性能与生产效率、延长工业机械有效寿命方面起着关键性的作用。

1985年，CHEN G等[1]研究了具有阻尼的线性弹性系统

u″(t)+Bu′(t)+Au(t)=0，

(1)

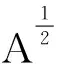
2014年，文献[12]利用算子半群理论及将方程中的二阶微分算子分解为两个一阶微分算子的技巧，在Banach空间X中研究了线性阻尼弹性系统

(2)

其中A：D(A)⊂X→X是扇形算子，ρ>0是常数，x0∈D(A)，y0∈X。并且给出了系统(2)相应半群是解析的指数稳定半群的充分条件。随后，文献[13-15]研究了系统(2)相应的非线性阻尼弹性系统mild解的存在性及整体解的指数衰减性。

本文将在Hilbert空间H中研究具有结构阻尼的线性弹性系统

(3)

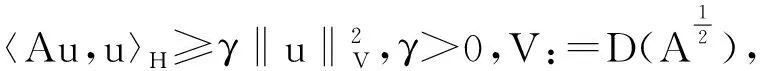
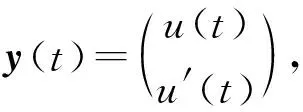
(4)

其中算子矩阵

其中D(Λ)=D(A)×D(A2)。

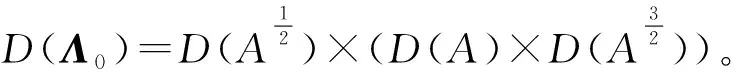
于是算子Σ定义了一个Λ与Λ0之间的酉等价，即

Λ0=ΣΛΣ-1，

(5)

1 预备知识

引理1(Lumer-Phillips定理)[16]设A是定义在Banach空间X上的线性子空间D(A)中的线性算子，则A生成一个压缩半群，当且仅当：

(1)D(A)在X上稠密；

(2)A是闭算子；

(3)A是耗散的；

(4)存在λ>0，使得A-λI是满射(I是恒等算子)。

定义1[17]算子A生成H上的C0-半群T(t)(t>0)是指数稳定的，是指存在常数M≥1及μ>0，使得‖T(t)‖≤Me-μt，t≥0。

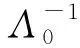
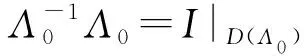
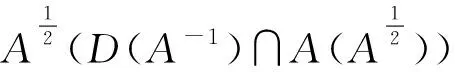
为了方便讨论，设Λ(t)(t≥0)为算子Λ生成的C0-半群，S(t)(t≥0)为算子Λ0生成的C0-半群。

引理2 设-A是Hilbert空间H上稠定闭耗散算子，即

Re〈-Au,u〉H≤0，u∈D(A)，

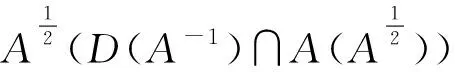
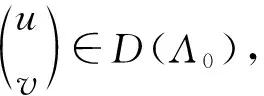
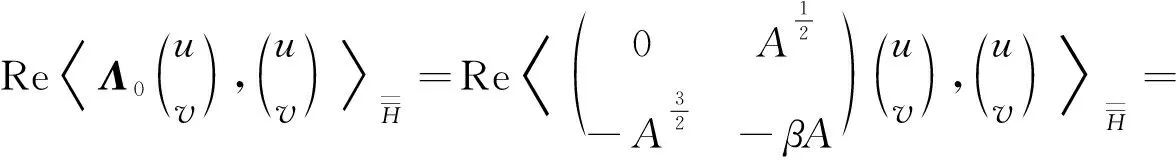
Re〈-βAv,v〉H≤0，

即Λ0是耗散的。

其中ωs(Λ)是Λ的谱界。则etΛ(t≥0)指数稳定的充要条件是半平面{λ=a+ib∈C：a>0，b∈R}包含在算子Λ的预解集ρ(Λ)中，且预解式满足

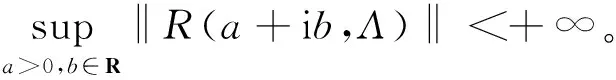
2 主要结论

这一部分，将研究系统(4)的渐近稳定性。

定理1 设A:D(A)⊂H→H是自共轭算子，β>2，则存在算子

使得对于任意的y1,y2∈D(A)，有下列估计成立：

(6)

其中

并且

即系统(4)在这种情况下是指数稳定的。

证明由Lyapunov方程

(7)

可得

(8)

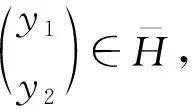
(9)

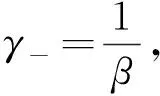
另一方面，对于固定的y1，有

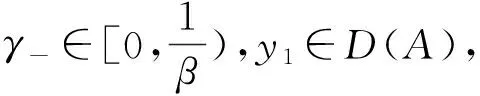
(10)

设σ(-A2)为-A2的谱，则-A2的谱界ωs(-A2)表示为

ωs(-A2)={Reλ：λ∈σ(-A2)}，

有

并且

通过计算，很容易得到

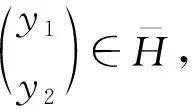
且有

最后，考虑系统(4)的mild解y。由(7)式可得

由(6)式可得

即

因此，有

即

则有

即系统(4)在这种情况下是指数稳定的。

定理2 设A：D(A)⊂H→H是自共轭算子，β>2，且满足

(11)

及

-Re〈Av,v〉H≤|Im〈Av,v〉H|，∀v∈D(A)。

(12)

又设0<δ≤δ-a<1<β，且δ-β

成立，则

(13)

由(13)式，易得

即

(14)

进一步，考虑(14)式的实部和虚部，有

|a+Re〈βAu,v〉H|<δ，

(15)

和

|b+2Im〈A2u,v〉H+Im〈βAv,v〉H|<δ，

(16)

结合(11)式和(15)式可得，

(17)

即

(18)

由(13)式，有

由上式可得

所以，由(18)式，有

|b+2Im〈A2u,v〉H+Im〈βAv,v〉H|<3δ，

结合(12)式、(17)式和(18)式，有

|b|(1+a-δ)≤3δ-|Im〈βAv,v〉H|≤3δ+Re〈βAv,v〉H<4δ-a，

即

证毕。

ωg(Λ)<0。