等离子体湍流能量传输的尺度相关性
2021-03-02万敏平ValentiniFrancescoMatthaeusWilliam史一蓬陈十一
杨 艳, 万敏平, Valentini Francesco, Matthaeus William H, 史一蓬, 陈十一
(1. 南方科技大学, 广东深圳 518055; 2. 卡拉布里亚大学物理系, 意大利科森扎 87036; 3. 特拉华大学物理与天文系, 美国特拉华州纽瓦克 19716; 4. 北京大学, 北京 100871)
引 言
湍流普遍存在于空间等离子体中, 如太阳日冕不断向外膨胀从而形成的等离子体流——太阳风, 就呈现出湍流特征[1-4]. 等离子体湍流的高度非线性, 使其包含多尺度 (含能尺度区、惯性尺度区、耗散尺度区、离子尺度、电子尺度、Debye长度等)及多过程相互作用. 尺度间的能量级串是湍流研究中一个十分重要的概念, 能量从大尺度逐级向小尺度传递, 直至达到某一足够小的尺度, 能量通过黏性、电阻作用耗散成热. 基于以上物理图像, 学者们提出利用能量级串建立太阳风加热与太阳风湍流发展之间的关系[5]. 卫星观测发现太阳风从日冕向行星际空间膨胀的过程不是绝热膨胀冷却的过程[6], 高温太阳风加热机制是空间物理学的关键前沿课题之一. 此外, 恒星际、星系际间存在有超高能的粒子(宇宙线), 而关于粒子如何加速至高能是长期未得到解决的问题之一. 等离子体湍流耗散作为一种引起粒子加热加速的机制, 具有重要作用. 显然, 对等离子体湍流能量传输和耗散过程的研究有助于理解空间中的许多物理现象.
通过尺度l的能流率是能量传输过程中最基本的量, 能量在无穷大Reynolds数下的惯性区的传输是守恒的, 这意味着能流是常数. 值得注意的是, 这里的能流率指的是净能量传递, 即全场平均, 但局部的能量传输很有可能是间歇过程, 那么局部的能量传输可能与平均值有很大偏离. 为了给出局部的能量传输率, 采用滤波的方法[7]可以得到通过尺度l的亚格子能流Πl(x). 在中性流体湍流中, 局部亚格子能流的空间分布具有间歇性[8-9], 并且可正可负, 可以理解为从局部来看能量可能从大尺度传向小尺度, 亦可从小尺度传向大尺度. 对于等离子体湍流局部的亚格子能流的研究, 在近几年才引起关注, 如Yang等[10-12]采用可压缩磁流体动力学(magnetohydrodynamic, MHD)湍流数值模拟以及全粒子(particle-in-cell, PIC)模拟讨论局部亚格子能流的间歇性, Camporeale等[13]的研究表明, Hall磁流体(Hall magnetohydrodynmic, HMHD)湍流中, 大的局部亚格子能流倾向于在流场的相干结构处发生.
级串的能量被耗散成热最直接的方式是通过磁流体湍流的黏性耗散和电阻耗散, 然而在空间环境中, 带电粒子的平均自由程往往远大于研究对象的特征尺度, 于是一般认为空间等离子体是无碰撞的. 对于无碰撞等离子体湍流, 能量的耗散不能简单地由磁流体湍流模型的黏性、电阻耗散实现, 耗散区如何把扰动的能量传给无碰撞等离子体, 一直是学术界的争论焦点. 基于太阳风湍流的波动性, 太阳风加热所需的能量可能来自波动-粒子相互作用的波动能量[14-16], 如离子回旋波或动理学Alfvén波(kinetic Alfvén wave, KAW)的回旋共振耗散或Landau阻尼耗散. 此外, 数值模拟和卫星观测数据表明, 能量耗散主要在局部发生, 对应有相干结构(如电流片)[17-19]或磁重联[20-21]. 对于无碰撞等离子体能量耗散而言, 哪种机制起主要作用, 甚至哪种波动和粒子的相互作用起主要作用, 仍然是研究的热点.


1 能量传输通道的理论推导
对无碰撞等离子体, 可采用Vlasov方程进行统计描述,
式中,fα(x,v,t)为α粒子在相空间(x,v,t)的分布函数,α=i表示离子,α=e表示电子. 位置空间中的宏观量, 如密度、速度、压强、热流等, 可以通过分布函数的矩得到, 以量γ(v)为例, 速度空间积分后得到
1.1 电场做功及压强张量做功
如果把γ(v)取为α粒子的质量mα, 动量mαv, 能量mαv2, Vlasov方程的矩分别对应质量、动量和能量方程
(1)
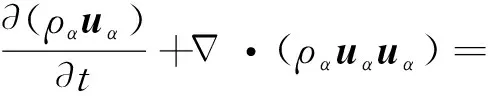
(2)
式中,qα为α粒子电荷量,ρα=mαnα为α粒子质量密度,nα为α粒子数密度,uα为α粒子的流体速度,Pα为压强张量,hα为热流矢量.
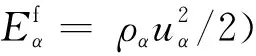
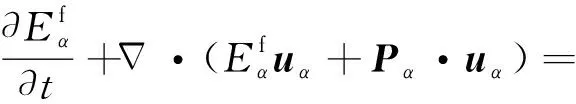
(3)
(4)
(5)
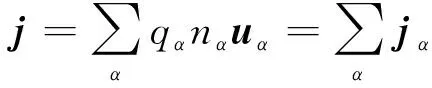
1.2 亚格子能流
为了研究各尺度间的能量传输, 可采用物理空间滤波器[30]. 低通过滤后的量可记为
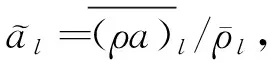
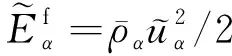
(6)
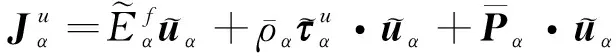

2 混合Vlasov-Maxwell模拟
混合Vlasov-Maxwell (hybrid Vlasov-Maxwell, HVM)模拟[31]是将等离子体系统看成由动理离子和流体电子组成, 本文中采用的是冷电子模型. 求解的方程包括3部分:
(1)Vlasov方程用以求离子分布函数fi(x,v,t)
(2)Ohm定律用以求电场E(x,t)
(3)Maxwell方程用以求磁场B(x,t)
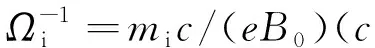
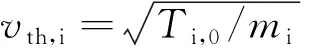
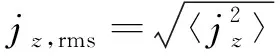
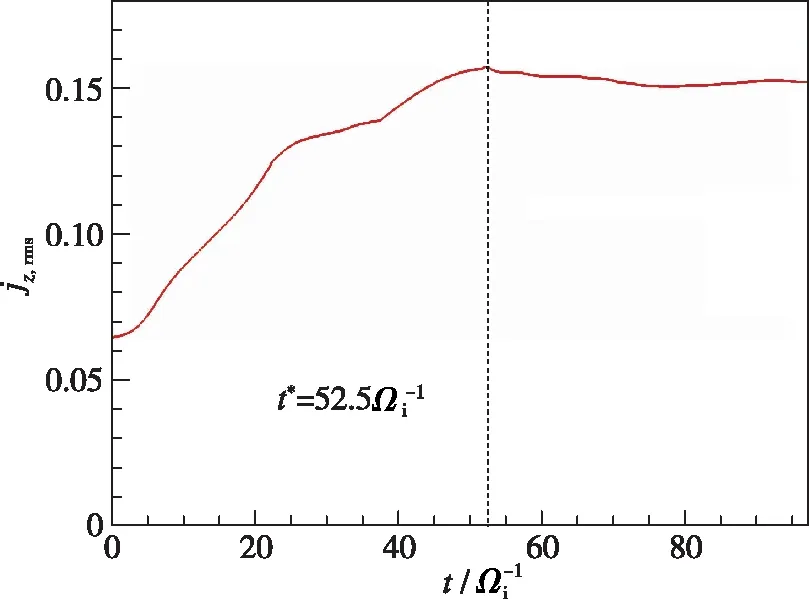
图1 z方向电流密度均方根随时间的变化Fig. 1 Temporal evolution of

图时刻, z方向电流密度jz的云图Fig. 2 Contour map of jz at
3 能量传输通道的区别与联系
等离子体湍流包含多种形式的能量, 如流体动能、内能、电磁能, 同时包含多个尺度, 尤其对于宇宙空间中无碰撞或弱碰撞的等离子体, 往往是非平衡的过程, 需要考虑电子、离子的动理学效应. 因此除了磁流体尺度(如含能尺度、惯性尺度、耗散尺度), 还需要考虑更小的动理学尺度行为. 对等离子体湍流的能量传输过程的研究, 可以采用不同的量对其进行表征, 本文将从尺度相关性以及空间相关性研究它们之间的区别与联系.
3.1 能量转换

将方程(3)作全场平均, 并对时间t进行积分, 可得到离子流体动能随时间的变化方程
(11)
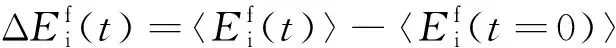
图4给出了磁能、离子内能、离子流体动能随时间的变化及电场做功和压强张量做功的时间积分. 图4(a)中磁能的变化与电场做功趋势一致, 它们之间的差异可能是由数值模拟的精度以及时间积分的精度所致. 图4(b)中离子内能的变化和压强张量做功几乎重合, 而图4(c)中离子流体动能的变化和电场做功(离子部分)及压强张量做功之和基本重合. 图4证实了电场做功表示磁能的损失, 其连接了磁能和流体动能, 而压强张量做功表示内能的增加, 其连接了流体动能和内能.
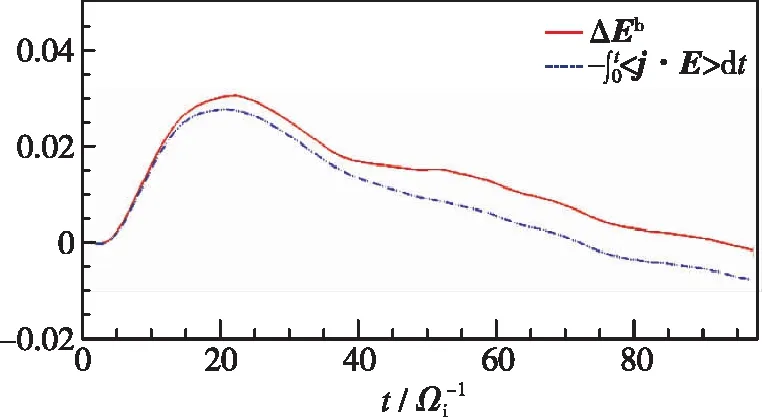
(a) Magnetic energy

(b) Ion internal energy
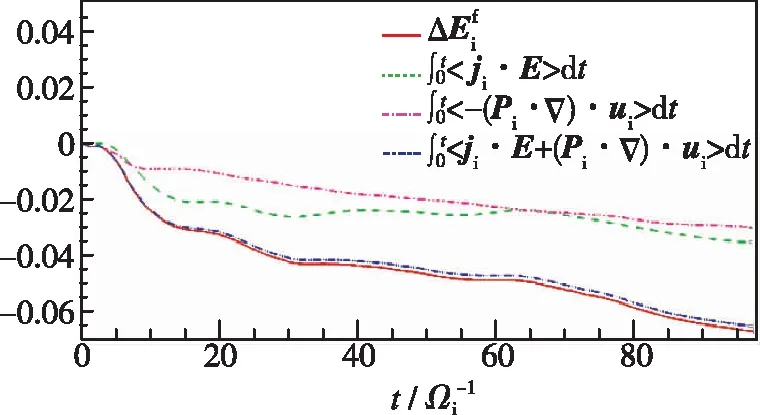
(c) Ion fluid flow kinetic energy图4 全场平均的磁能、离子内能和离子流体动能随时间的变化Fig. 4 Temporal evolution of magnetic energy, ion internal energy and ion fluid flow kinetic energy
3.2 主要作用尺度
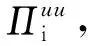
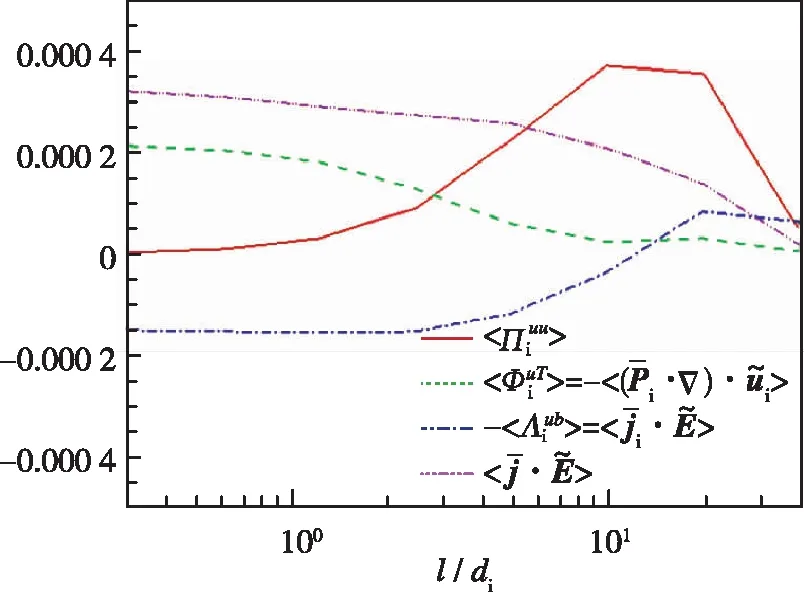
图5 全场平均的离子亚格子能流, 过滤后的离子压强张量做功, 离子部分电场做功, 总电场做功, 随过滤尺度l的变化Fig. 5 Volume integrated cross-scale energy transfer flux for ions, filtered pressure tensor work for ions, electric field work on ions and total electric field work, as a function of filtering length l
3.3 空间关联性

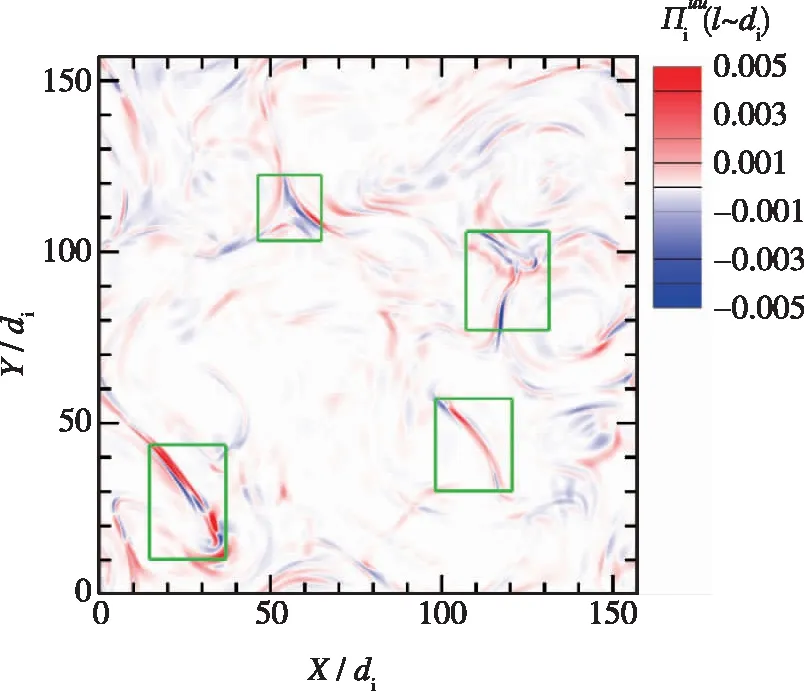
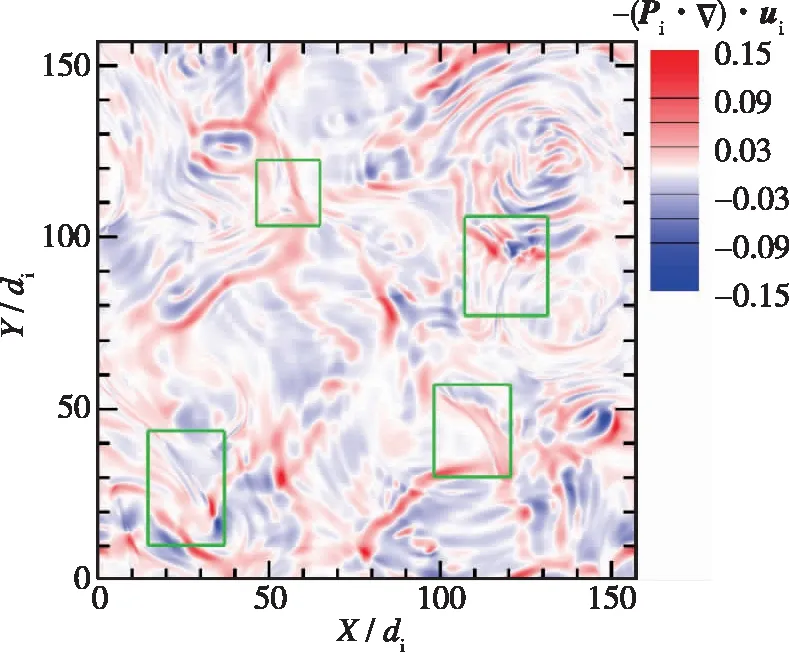
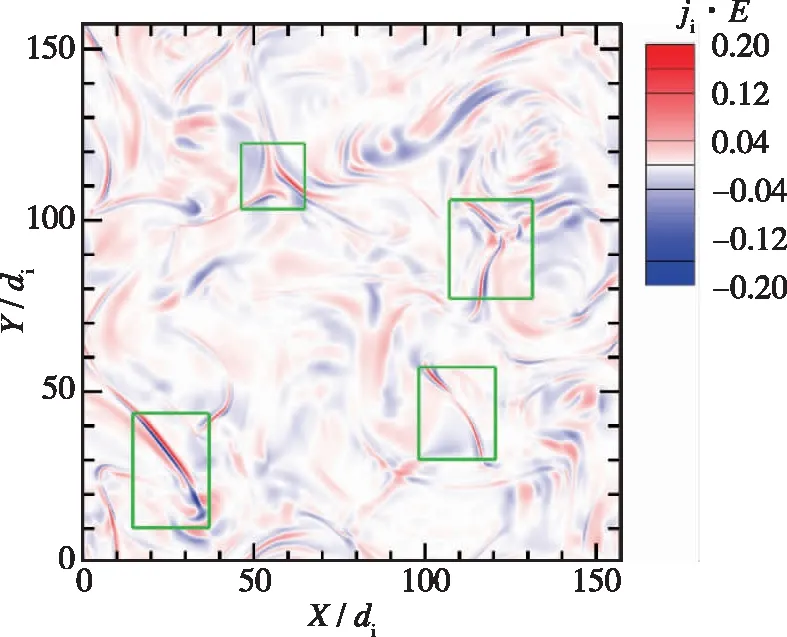
(c) ji·E
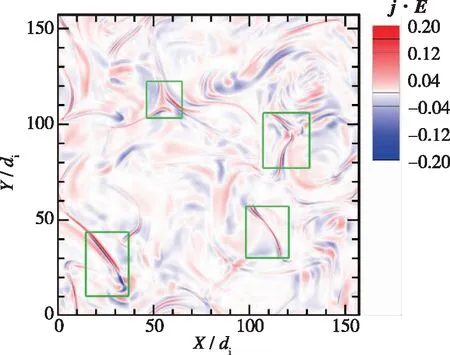
(d) j·E
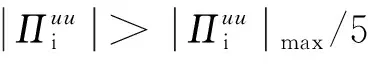
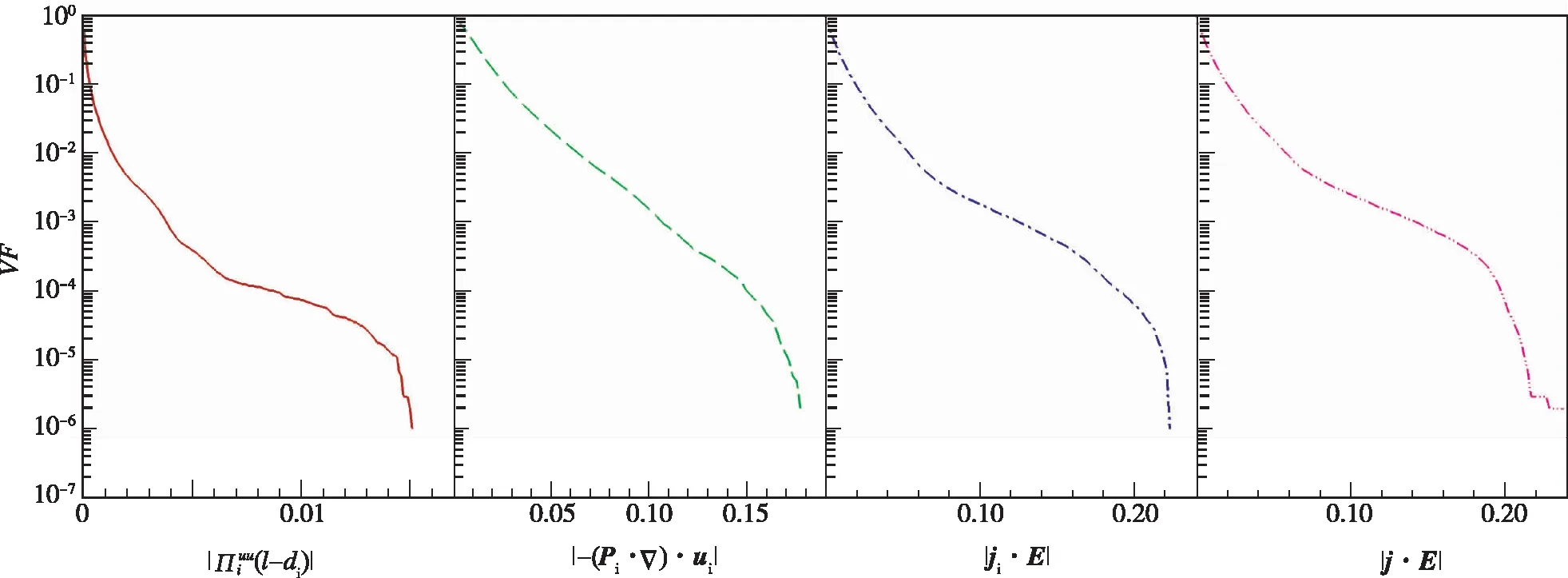
图7 离子亚格子能流, 离子压强张量做功, 离子部分电场做功, 总电场做功绝对值所占的空间体积(或面积)分数Fig. 7 Filling fraction of volume (or area) occupied by absolute values of cross-scale energy transfer flux for ions, pressure tensor work for ions, electric field work on ions and total electric field work
另一方面, 对比图6中不同能量传输通道的空间分布, 可发现它们的整体形态是非常相似的, 比如图6中绿色框标示的部分. 将图6与图2对比, 可看到各能量传输通道与电流密度的空间分布也存在一定相似性, 强相干结构处对应着强能量传输, 这与最近研究的结果[22-23, 36, 40-41]是一致的. 为了定量描述它们空间分布的相关性, 可采用不同量之间的统计相关函数, 例如两个量f,g之间的2阶空间相关函数可记作
图8给出了不同间距下各能量传输通道的相关函数, 可看出各能量传输通道的相关函数随着间距|r|的增大而快速减小. 如果利用R(f,g,rc)=e-1(其中e=2.71828…为自然常数)定义相关长度rc, 则可以得到各能量传输通道之间的相关长度大约为2di, 因此各能量传输通道对应的强能量传输的空间位置, 尽管可能不是完全重合, 但距离很近.
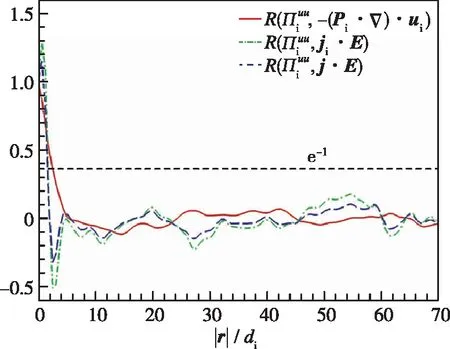
图8 离子亚格子能流, 离子压强张量做功, 离子部分电场做功, 总电场做功之间的2阶空间相关函数Fig. 8 Second-order spatial correlation functions of cross-scale energy transfer flux for ions, pressure tensor work for ions, electric field work on ions and total electric field work
4 结论
从Vlasov-Maxwell方程出发, 可推导出电场做功、压强张量做功、亚格子能流等能量传输通道. 本文通过物理空间滤波, 研究了各能量传输通道的尺度依赖性, 混合Vlasov-Maxwell模拟的结果表明, 电场做功主要集中在较大尺度, 而压强张量做功集中在小尺度, 其间伴随有尺度间的能量传输. 各能量传输通道的空间分布非常相似, 具有强间歇性, 并且与强相干结构相关, 即强能量传输倾向于发生在强相干结构处.
基于以上结果, 并结合近年数值模拟和卫星观测的结果, 可以大致概括等离子体湍流从磁流体尺度到动理学尺度的能量传输主要过程: (1)经典的能量级串概念[42-43]中, 能量从含能尺度输入, 在惯性区级串, 在能量级串的过程中电磁场与流场的间歇性出现, 不断形成多尺度的相干结构; (2)已有的研究表明, 电场做功集中在强电流片处[22-23], 本文结果表明电场做功实现了电磁能与流体动能之间的转化; (3)已有的研究表明, 速度梯度张量会导致压强张量各向异性的产生[37], 于是压强张量做功集中在强变形拉伸(涡结构)处[12,29,37], 本文结果验证了压强张量做功能实现流体动能和内能之间的转化, 该过程主要发生在小尺度.
致谢第一作者感谢南方科技大学校长卓越博士后基金及国家自然科学基金(11902138)的资助. 第二作者感谢国家自然科学基金(91752201, 11672123)的资助. 本研究工作得到南方科技大学科学与工程计算中心支持.
