三维菱形液舱剧烈晃荡和共振频率数值研究
2021-03-02辛建建石伏龙
辛建建, 方 田, 石伏龙
(1. 宁波大学 海运学院, 浙江 宁波 315211; 2. 中国船舶科学研究中心, 江苏 无锡 214082;3. 武汉理工大学 交通学院, 武汉 430063)
风浪中航行的储液船舶,如液化石油气(LPG)、液化天然气(LNG)船,在受到外部激励时,液体会对容器壁产生强烈的砰击作用,造成结构的变形甚至破坏,对船舶稳性和结构强度造成严重威胁.液体发生晃荡时会伴随产生波面破碎、波对舱壁的高速砰击、液滴形成及气泡卷入等强非线性现象.而且,晃荡引起的砰击载荷会对舱壁产生强烈的局部冲击,影响船舶的稳定性,甚至破坏液舱的围栏系统,导致沉船事故.因此,研究晃荡现象和预报晃荡砰击载荷对液舱结构设计和船舶的安全运营至关重要.
在过去,模型实验[1]和解析半解析方法[2]是船舶液舱晃荡研究的常用手段.然而,模型实验费用昂贵、条件苛刻(如低温),解析方法局限于简单几何形状液舱中的晃荡问题. 随着计算机技术的飞速发展,数值方法处理晃荡问题显示出较大的优越性,可以克服解析方法无法解决的困难,诸如液面大变形、摇荡运动影响等.与费用昂贵、时间较长的模型实验相比,数值模拟方法的成本低廉、灵活方便.从自由表面跟踪技术分,有流体体积分数(VOF)法[3]、水平集(Level Set)法[4]和光滑粒子流体动力学(SPH)法[5]等.根据计算网格可分为贴体网格法[6]、直角网格法[7]和无网格法[5].
在绝大多数的晃荡流模拟中,对象为矩形液舱,边界条件能直接施加,因为计算网格与液舱边界重合.然而在实际工程应用中,液舱可能是任意形状如菱形和椭圆形,另外液舱中也有可能存在内部结构如横隔板.为了处理非矩形液舱或具有内部结构的情况,一个常用方法是贴体网格法[6].例如,Jiang等[8]基于 OpenFOAM模拟了菱形液舱的晃荡问题,Zhao等[9]基于重叠网格法模拟了部分充液 LNG 液舱的三维晃荡流.然而,对于多自由度激励、三维复杂形状液舱和多个内部结构存在的情况,贴体网格方法面临挑战.为了处理这些问题,直角网格方法是一个具有吸引力的替代方法.在直角网格方法中,液舱边界并不与背景网格线重合,通过引入力源项或重构浸入边界的插值模板以施加边界条件.为了表示不规则边界或内部结构物对晃荡流的影响,Kim等[10]引入一个缓冲层以施加液舱斜边界附近的自由表面边界条件.Lee等[11]通过引入一个二次多项式内插格式以施加液舱不规则边界的无滑移边界条件,根据不规则边界与网格线之间的相对位置关系,内插模板分为 13 种情况.
目前,三维复杂液舱剧烈晃荡的数值预报仍面临巨大的挑战,文献中也鲜见对菱形液舱共振晃荡频率的研究.为此,本文采用一个基于直角网格的三维多相流模型模拟了菱形液舱剧烈晃荡问题,并预报了菱形液舱的共振频率,重点专注于舱壁冲击压力和全局晃荡流运动,忽略局部物理现象湍流和可压缩的影响.在规则网格上求解不可压缩黏性N-S方程,在长方体四角布置4个楔形体以表示菱形斜边,采用径向基函数虚拟网格法[12],通过在固体区域内部布置合适的虚拟网格,以考虑不规则边界对流场的影响.
另外,采用一个三维梯度增量Level Set(GALS)两相流模型[13]捕捉强非线性自由表面.基于所开发的模型,模拟了菱形液舱的大幅晃荡现象,并进行了数值收敛性验证.进一步研究了不同充液水深下壁面冲击压力随激励频率的变化规律,确定了菱形液舱的共振频率,以期为LNG船舶的液舱结构设计提供理论和技术指导.
1 数学模型
不可压缩N-S方程由描述任意流场的质量和动量守恒方程组成.在三维直角坐标系下,非定常黏性不可压缩N-S方程表达如下:
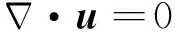
(1)
(2)
式中:速度向量u=[uvw],u、v、w分别是直角网格x、y和z方向上的速度分量;t为时间;ρ为密度;p为压力;υ为流体的运动黏性系数.对于外部激励力fa,其在多数自由表面流动中为重力加速度g.然而,对于晃荡问题,外部力包括重力和晃荡运动引起的惯性力以考虑液舱壁面运动对舱内流场的影响,其表达式为[7]
(3)
式中:V和Ω分别为非惯性坐标系下的平移和旋转速度;r和R分别为网格节点坐标和旋转中心.式(3)右边5项分别是非惯性坐标系的重力加速度、平移、旋转、离心及科氏加速度.
对于自由表面的捕捉,通过求解GALS方程实时更新距离函数φ和梯度ψ以隐式捕捉两相界面.GALS方程[14]表示为
(4)
(5)

在两相流模式计算中,根据自由表面的位置变化,定义在计算网格单元中心密度ρ及黏性系数υ的计算公式为
ρ=Hε(φ)ρW+(1-Hε(φ))ρA
(6)
υ=Hε(φ)υW+(1-Hε(φ))υA
(7)
式中:Hε(φ)为Heaviside函数以区分流体和空气界面的流体属性;ρ及υ的下标W和A分别表示水和空气.为了减缓因密度(或黏性)介质的跳跃对流动的影响,使得过渡层内物性参数光滑变化,抑制数值振荡.
2 数值求解方法
2.1 N-S方程求解器
在本文研究中,基于自主开发的时间半隐式有限差分法,在交错直角网格上求解非定常不可压缩N-S方程.采用分步法解耦速度和压力,TVD-RK2(Total Variation Diminishing Second-order Runge-Kutta)格式进行时间推进,对流项采用时间显式处理,黏性项采用Crank-Nicolson格式半隐式处理.对于空间离散,对流项采用高阶TVD-MUSCL(Monotonic Upstream-centered Scheme for Conservation Laws)格式离散,黏性项以中心差分格式离散.另外,对于压力泊松方程离散形成的大型稀疏线性方程组,采用预处理的BICGSTAB(Bi-conjugate Gradients Stabilize)方法结合一种对角存储格式求解.更多的细节请参考文献[12].
2.2 GALS方法数值求解
GALS方程式(4)、(5)以特征形式表示为
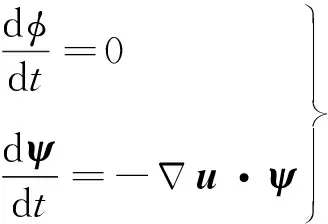
(8)
求解过程分为两步:① 采用Shu-Osher RK3方法从t+Δt到t进行向后时间积分求解特征曲线方程∂x(τ)/∂τ=u(x(τ),τ);② 然后沿着特征曲线采用显式梯度格式进行向前积分求解式(8)以更新φ和ψ.值得注意的是在任意位置的变量φ和ψ通过Hermite立方多项式插值得到以获得三阶精度,另外,通过对Hermite立方多项式格式进行微分以解析方式计算φ和ψ的一阶和二阶导数.详细求解过程参考文献[13].
2.3 不规则边界处理
浸入边界法的网格生成过程简单,但由于浸入边界本身并未包含在计算网格中,精确表示背景网格中浸入边界的存在是个难点.本文采用基于径向基函数(RBF)的隐式等值面表示方法[12],光滑基函数拟合离散的物面控制点以构造任意复杂物体的等值曲面,并且根据等值面距离函数的正负号识别场点属性.下一步就可重构虚拟网格的流体变量值以施加边界条件.通过在浸入物体内部布置有限数量的虚拟网格以表示静止或运动边界的存在,以适当的插值模块及技术(如双线性插值方法),施加浸入动边界条件.
虚拟网格的插值重构过程可细分为3步:标记镜像点、插值重构和满足镜像条件.首先,对于每个虚拟网格(GC),沿着物体表面的外法向从虚拟网格单元中心延伸到流体域以确定唯一的一个镜像点(MP),如图1所示.然后采用三线性插值格式计算每个镜像点的流体变量.然而,存在一个或更多的模板点是虚拟网格本身的情况,为了避免繁琐的内插模板分类过程,首先对封闭镜像点(MP)的8个邻近网格节点进行判断.如果该网格节点为流体网格点(FC),则将它确定为模板点,1、2、3、4即为二维插值格式中识别出的模板点,如图1(a)所示.如果为虚拟网格点(GC),则相应的边界点(BP)作为模板点,而不是虚拟网格点本身,如图1(b)所示.如果更多的邻近网格点识别为虚拟网格点,同样,相应的边界点BP作为模板点(见图1(c)).在求得镜像点的流体变量后,虚拟网格点的流体变量可通过满足物面的镜像条件直接得到.当通过标准的七点中心差分格式在整个计算域求解N-S方程后,物面边界条件就会得到隐式施加.更多的求解细节见文献[12].
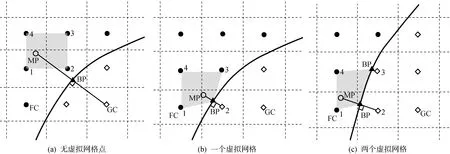
图1 虚拟网格法的二维插值格式Fig.1 Two-dimensional interpolation format of virtual grid method
3 三维菱形液舱晃荡分析
为研究复杂液舱系统下的晃荡特性,数值模拟了不同水深和激励频率下横摇激励的三维菱形液舱晃荡问题.根据Mikelis等[15]对不同充液水平下棱形液舱的晃荡实验研究,液舱模型的长、宽、高分别为L=0.741 m、W=0.399 m、H=0.405 m,其几何模型如图2所示.液舱遭受强迫横摇激励,横摇中心Y1、Y2在x轴中心位置距离液舱底部0.194 m.液舱横摇激励的运动描述为θy=θ0sinωt.θy为绕横摇中心Y1、Y2的横摇角;横摇幅值θ0=0.1 rad;ω为激励频率,ω=2π/T,T为横摇周期.在右壁面宽度方向中心位置设置7个压力传感器R1~R7,距离液舱底部的距离分别为0.075,0.113 5,0.205,0.296 5,0.341,0.390,0.405 m,R7距离右壁面0.02 m.在宽度中心距离左边界 0.135 6 m位置设置浪高仪WR.在液舱所有边界设置速度无滑移边界条件,在上壁面设置压力为0,其余边界设置Neumann边界条件.由于采用规则的矩形计算区域,为了考虑菱形液舱的斜边界对流场的影响,在液舱横剖面的四角布置4个楔形体,采用虚拟网格法施加楔形体表面的物面边界条件.
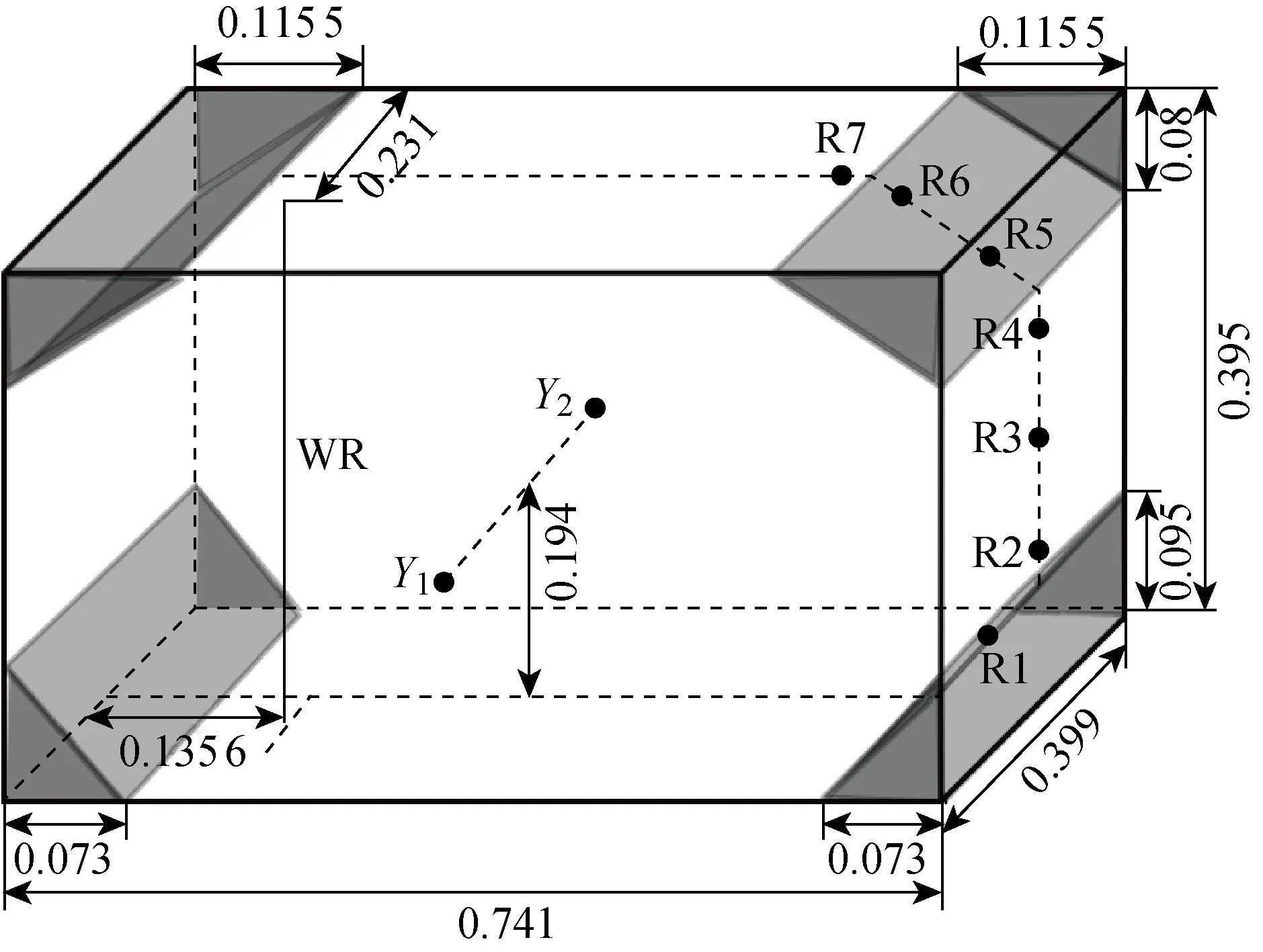
图2 菱形液舱几何模型和传感器布置(m)Fig.2 Geometrical model of prismatic tank and placement of sensors (m)
3.1 数值验证
首先模拟了充液比h/H=0.9 (h为水深)和周期T=0.97 s的工况以验证本文多相流方法的精度和可靠性.分别采用80×50×60、100×60×80和120×80×100的3套网格离散计算区域以研究网格收敛性,根据CFL(Courant-Friedreichs-Lewy)条件决定变时间步长,其中时间松弛系数设置为ωCFL=0.3.本文方法3套网格下计算的在R3点的压力和WR位置的波浪爬高与实验结果进行了比较,如图3所示.图中η为波浪爬高.在3套网格下的压力和波浪幅值与实验数据吻合较好,尽管观察到峰值压力有略微差别.然而,随着网格细化,峰值压力逐渐趋近实验数据,如图3(a)所示,验证了本文方法良好的网格收敛性.另外,波峰在η=0.4 m的位置发生截断,因为波浪爬升到了液舱顶部.为了研究时间步长的收敛性,选择3个不同的时间松弛系数ωCFL=0.1、ωCFL=0.3和ωCFL=0.6,分别在x、y和z方向选用100×60×80的计算网格.图4展示了3个时间松弛系数下计算的压力和波浪爬升与实验数据的比较结果.总体而言,在3个时间松弛系数下本文计算结果与实验数据吻合.随着时间步长的缩小,压力峰值会更加尖锐,更趋向于实验结果,ωCFL=0.1和ωCFL=0.6时的压力峰值相比实验数据分别略小4.8%和7.1%,偏差在合理范围内,再一次验证了本文方法的精度和不同时间步长下的可靠性.为了在求解质量和计算成本间取得平衡, 在其他工况计算中时间松弛系数选为ωCFL=0.3,网格设置为100×60×80.

图3 h/H=0.9时三套网格下本文方法和实验得到的压力和波浪爬高时间历程Fig.3 Time history of pressure and wave elevation by present method on three grids and experiment at h/H=0.9
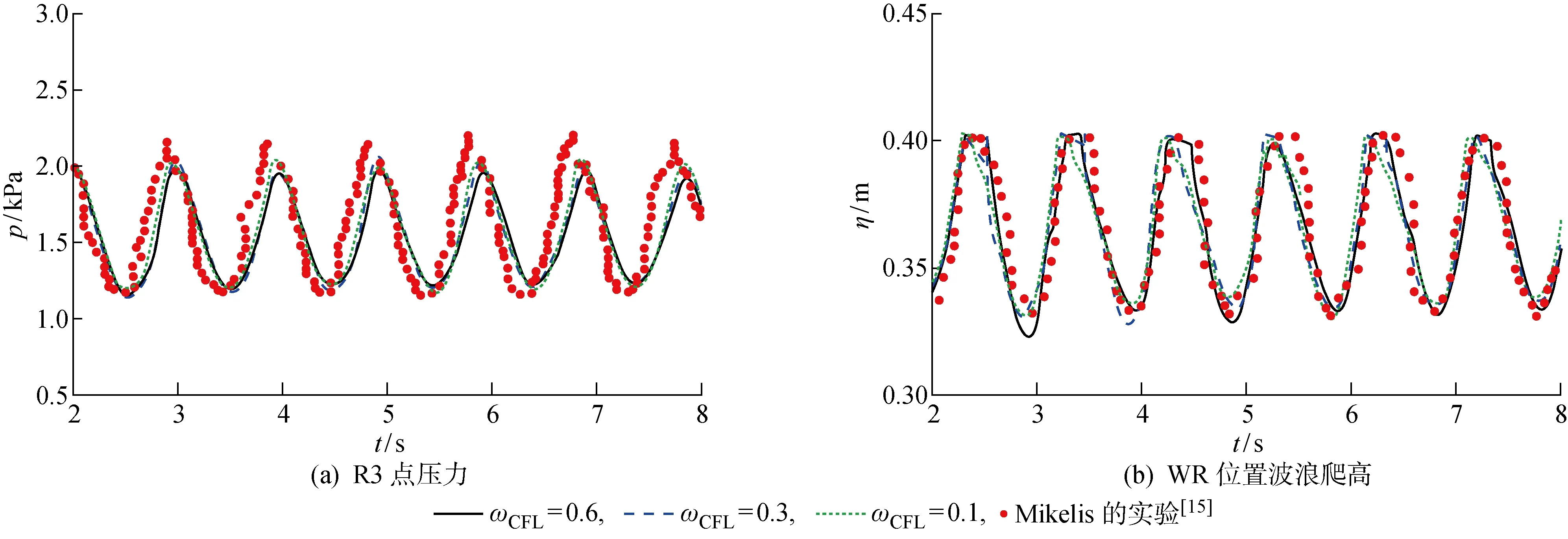
图4 h/H=0.9时三个时间松弛系数下本文方法和实验得到的压力和波浪爬高时间历程Fig.4 Time history of pressure and wave elevation by present method on three time coefficients and experimental data at h/H=0.9
分别模拟了h/H=0.3、T=1.517 s和h/H=0.61、T=1.112 s的两个工况以进一步验证本文方法的可靠性.图5、6分别为两个工况下波高和3个测量点压力与Mikelis等实验数据的比较结果.当h/H=0.3时,在垂向壁面R2点的压力脉冲值略高于实验结果,自由表面曲线在波谷与实验值吻合,但波峰略高于实验值(见图5).当水深继续增加到h/H=0.61时,压力变化趋势和形态与实验结果吻合,自由表面曲线的波高略大于实验值(见图6).本文结果与实验值的偏差可能是由于湍流或空气可压缩的影响所致,考虑到三维晃荡的复杂性、非线性和瞬态性,偏差在合理范围内.从图5可看出,晃荡波周期性地砰击壁面产生脉冲形压力曲线.同时,在每个周期内出现连续的双波峰现象,其由强烈的非线性波浪砰击产生.当液舱运动到一侧时,流体被高速运动液舱驱动到同一侧,快速运动的水体砰击垂向壁面,导致第1个压力峰值产生,尽管液舱达到最大横摇角,但水体在惯性作用下继续向前运动,导致第2个压力峰值产生.当水深增加到h/H=0.61时,由于此时晃荡流的非线性程度降低,压力曲线呈现周期性的单压力峰值现象,自由表面曲线呈现较为规则的正弦曲线变化趋势,R2点的压力呈现周期性的简谐振荡特性,均衡压力在 1 250 Pa左右,该点在静水面以下,砰击压力由静水压力和动压共同主导.

图6 h/H=0.61时的的压力和自由表面时间历程Fig.6 Time history of pressure and free surface at h/H=0.61
图7、8分别为两个工况下在两个瞬时时刻的三维波面图,其中4个蓝色楔形体表示菱形液舱的几何外形,用来考虑不规则边界与流场的相互作用.h/H=0.3时,整个水体随着液舱摇荡向一侧产生剧烈运动,水体上层流体速度大于底部流体,形成大的涌浪,如图7(a)所示.当液舱达到最大横摇角时,涌浪砰击壁面,随后,液舱向反方向运动,驱动水体向反方向运动,并形成相同的涌浪,如图7(b)所示.h/H=0.61时,水体跟随着液舱运动并一直爬升到液舱顶部斜边,生成陡峭的、与上斜边贴合的非线性波浪.当波浪爬升到斜边最大位置时,其在重力作用下下落,形成波浪翻卷,同时,后方的波浪继续向前运动,形成皱褶形的波浪纹,如图8所示.
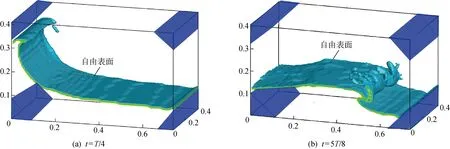
图7 h/H=0.3时两时刻的瞬时自由表面Fig.7 Instantaneous free surface at two moments at h/H=0.3
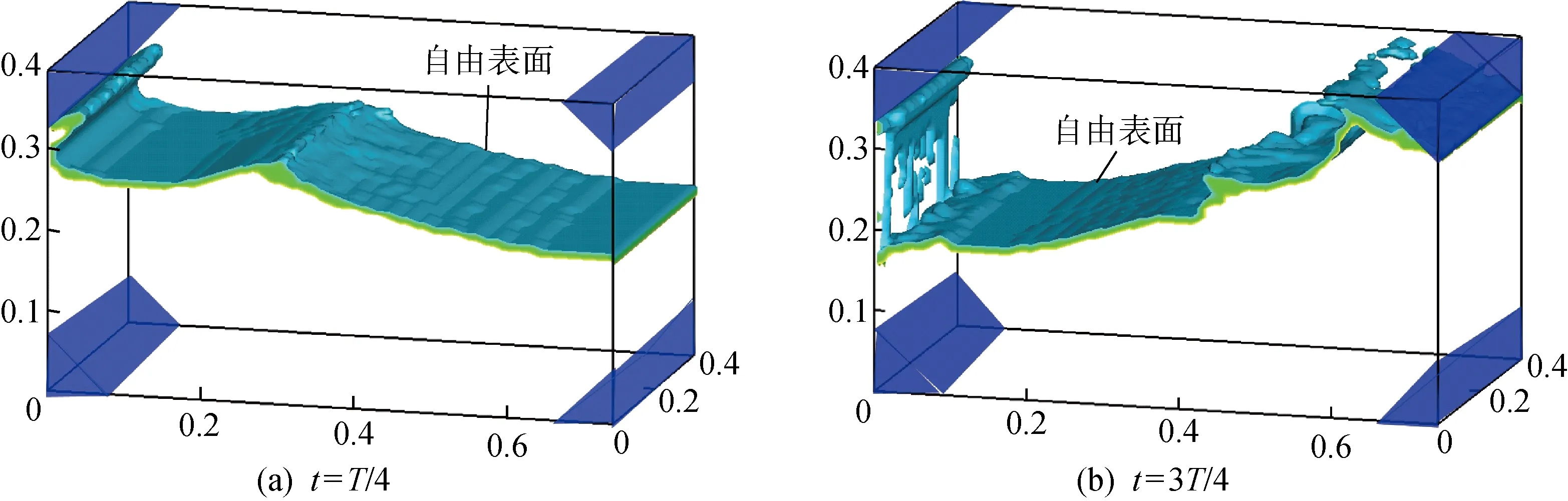
图8 h/H=0.61时两时刻的瞬时自由表面Fig.8 Instantaneous free surface at two moments at h/H=0.61
3.2 共振频率预报
在载液船舶液舱设计中,液舱共振频率(共振频率≈自然频率)预报对于避免危险工况的发生、保障航行安全具有重要的意义.对于矩形液舱,液舱自然频率可解析计算为
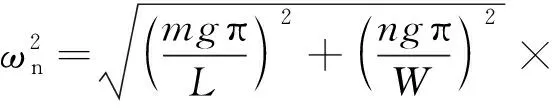
(9)
m,n=0, 1, 2, …
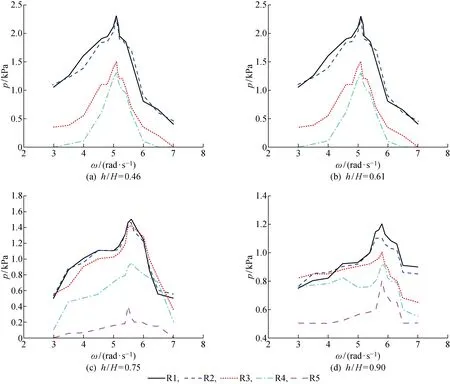
图9 4个充液水深下舱壁压力幅值与激励频率之间的关系Fig.9 Pressure amplitude at tank walls versus excitation frequency at four filling water levels
然而,对于不规则形状液舱如菱形液舱,其自然频率无法解析计算得到.鉴于此,本文数值研究了不同水深下液舱激励频率与舱壁局部位置压力幅值之间的关系,进一步确定了不同水深下菱形液舱的共振频率.图9展示了4个充液水深下舱壁压力测量点上的压力幅值随液舱激励频率的变化趋势,压力幅值取稳定状态时5个周期压力峰值的平均值,以避免初始扰动和瞬时波动的影响.可以看出,随着激励频率的增加,舱壁各点处的压力幅值迅速增加到最大值,当激励频率继续增加时,压力幅值迅速减小,而且压力幅值减小的速度大于增加的速度.压力幅值最大时对应的激励频率即为共振频率,也就是自然频率.由此可得到不同水深下菱形液舱的自然频率,如表1所示.为了提供参考,计算了相同主尺度下矩形液舱的最低阶自然频率,此时m=1,n=0.由表1可看出,相同水深下菱形液舱的最低阶自然频率小于相同主尺度下矩形液舱的最低阶自然频率,原因可能是液舱与晃荡流体强烈的非线性相互作用.应该指出的是,本文预报激励频率的精度为小数点后一位,因为采用的最小激励频率间隔是0.1 rad/s,为了提高预报精度,需要取更小的激励频率步长.

表1 4个充液水深下矩形液舱和菱形液舱的自然频率Tab.1 Natural frequency of rectangular and prismatic tanks at four filling water levels
随着水深的增加,自然频率增加,与式(9)一致.而且,随着水深的增加,晃荡波浪产生的冲击压力幅值逐渐减小,从h/H=0.46时P1点的 2 300 Pa到h/H=0.46时P1点的 1 200 Pa.从3.1节也可看出,随着充液比的增加,壁面冲击压力的非线性变化特征逐渐减弱,从h/H=0.3时的双压力峰值现象过渡到h/H=0.61时的单压力峰值现象,最后在h/H=0.9时呈现规则的正弦曲线变化特征.因为随着充液比的增加,晃荡液体的运动幅值会更多受到周围液体黏性阻尼作用的约束,而且在高充液比如h/H=0.75或0.9时,从图9(c)、9(d)中点P5的压力幅值可看出,晃荡波浪砰击到液舱顶部,顶部砰击的阻尼作用也会对波浪的非线性产生抑制作用.另外,在充液比h/H=0.46或0.61时,底部斜边点P1和壁面下部P2点遭受巨大的冲击压力,超过 2 000 Pa,壁面中上部的冲击压力也较大,接近 1 500 Pa,如图9(a)、9(b),说明此水深下整个垂向壁面都遭受较大的砰击载荷,液舱壁的整体强度需要加强.在充液比增加到h/H=0.75或0.90时,舱壁的整体冲击压力显著降低,但舱壁上斜边和顶部会遭受显著的冲击压力.由此可知,载液船舶在海上航行时,理想的充液水深是接近满载时.当充液水深近似为液舱高度一半时,液舱处于非常不利的工作环境.
4 结论
采用基于直角网格法的三维多相流模型模拟了横摇激励下菱形液舱大幅晃荡问题,研究了不同水深下舱壁局部位置压力幅值与激励频率之间的关系,得出菱形液舱的共振频率,主要结论有:
(1) 高充液比下晃荡研究表明本文计算模型具有良好的网格和时间收敛性,不同充液比下的冲击压力和波浪爬高也与实验数据吻合,验证了本文方法的精度.
(2) 随着充液比增加,壁面冲击压力的非线性变化特征逐渐减弱,从充液比h/H=0.3时的双压力峰值现象过渡到h/H=0.61时的单压力峰值现象,最后在h/H=0.9时呈现规则的正弦曲线变化特征.
(3) 同一充液比下菱形液舱自然频率低于同主尺度矩形液舱的自然频率,随着充液比增加,最大的压力幅值逐渐减小,因为有更多的黏性阻尼作用,而且高充液比时,也存在顶部砰击的阻尼作用.
(4) 当充液水深近似为液舱高度一半时,整个液舱垂向舱壁都遭受较大的砰击载荷,液舱处于非常不利的工作环境.
