电厂脱硫系统闭环子空间辨识方法研究

杨大州，张寻，姜昊，刘畅，李益国

(1.大唐环境产业集团股份有限公司特许经营分公司，南京 211106；2.东南大学能源与环境学院，南京 210096)

近年来，大气污染问题日益严峻，电站煤燃烧排放的大量SO2则是大气污染的主要污染之一[1]。烟气脱硫技术是世界上唯一大规模商业化应用的脱硫方法，其中，石灰石-石膏湿法烟气脱硫技术是应用最广泛和最成熟的脱硫工艺技术。但是，脱硫系统是一个典型的大惯性和非线性的多变量控制系统，传统的PID控制难以满足脱硫系统的控制要求。

为了研究电厂脱硫系统控制策略，建立高精度数学模型是首要工作。目前最常见的系统建模方法主要有机理建模方法与数据辨识建模方法。机理建模需要熟知控制系统的内在机理，且计算复杂，而电厂脱硫系统的被控对象往往具有非线性以及大惯性的特点，且脱硫工艺流程繁多，系统特性复杂，不适合应用机理建模方法；其次，当脱硫系统自动控制投入时获得的运行数据，其输入变量和输出变量之间存在相关性，采用最小二乘法等一般的开环辨识方法难以实现对模型参数的无偏估计；再者，从自适应控制的角度看，为了应对脱硫系统的慢时变特性，也需要研究系统的闭环辨识方法。

子空间辨识方法可以直接获得被控对象的状态空间模型，便于进行多变量预测控制器的设计。本文采用两种多变量闭环子空间辨识方法，建立脱硫系统的两输入两输出的状态空间模型，并与开环子空间辨识方法进行仿真比较与动态特性分析。

1 湿法石灰石脱硫系统

湿法石灰石烟气脱硫技术是目前世界上最广泛使用和最成熟的脱硫工艺技术，采用石灰石作为脱硫吸收剂，除去烟气中的SO2[2]。该技术脱硫效率较高，运行较为可靠稳定，并且能够适应大容量机组和高浓度SO2烟气条件。但是，湿法石灰石脱硫系统的控制问题是其发展的最大阻碍之一。

典型的湿法石灰石烟气脱硫系统可划分为烟气系统、吸收塔系统、石灰石浆液制备系统与石膏脱水系统，其中最核心的子系统是吸收塔系统，吸收塔内脱硫过程示意图如图1所示。几乎整个脱硫反应都是在吸收塔内完成的。

图1 吸收塔内脱硫过程示意图

原烟气降温后从吸收塔底部进入。新鲜石灰石浆液从浆液槽送入，与反应后下落至浆液槽的石灰石浆液相互混合。混合后的浆液通过循环泵实现循环使用，而经过结晶沉淀后的石膏等副产品被不断吹扫防止聚集，并被运送到储蓄罐中。吸收区内，循环浆液从吸收塔顶部由喷嘴喷出，自上而下的浆液与自下上升的烟气逆向接触，发生一系列化学反应，除去烟气中的SO2。净化后的烟气经升温后从烟囱排出。

2 闭环子空间辨识方法

闭环子空间辨识方法越来越受到关注，相较于开环辨识方法，其用于脱硫系统辨识有以下几点优势：

1)由于工业生产过程常常具有很大的干扰，开环辨识会使得系统在大范围内变得非线性；

2)闭环辨识有利于控制系统的设计，闭环辨识所得到的模型在控制算法设计相关的频率范围内是相当准确的，而且对于一些特殊的控制系统设计方法，闭环辨识的方差也要小于开环辨识；

3)闭环子空间辨识大多数都有在未来输入的补空间进行正交投影计算的步骤，从而可将噪声项消除[3]。

目前国内外闭环子空间辨识方法应用较多的方法主要有基于正交投影的闭环子空间辨识方法(Closed-loop Subspace Orthogonal Projection Identification Method，CSOPIM)[4]与基于新息估计的闭环子空间辨识方法(Parallel parsimonious SIM with Estimation，PARSIME)[5]。

2.1 子空间辨识的基础知识

考虑如下的离散线性时不变状态空间模型：

(1)

式(1)中，xk∈n为系统的状态变量；uk∈nu为输入观测向量；yk∈ny为输出观测向量；wk∈n与vk∈ny分别为系统的测量噪声与过程噪声。

假设系统是能观测的，可设计如下Kalman滤波器：

(2)

式(2)中，K为卡尔曼滤波增益。

(3)

式(3)中，新息ek为零均值白噪声。

定义输入数据Hankel矩阵Up与Uf：

定义状态序列Xi=[xixi+1…xi+j-2xi+j-1]∈n×j，则过去状态序列为Xp=X0=[x0x1…xj-2xj-1]，未来状态序列为Xf=Xi=[xixi+1…xi+j-2xi+j-1]。

首先考虑以下状态预测方程：

x1=Ax0+Bu0+Ke0

x2=Ax1+Bu1+Ke1

(4)

=A(Ax0+Bu0+Ke0)+Bu1+Ke1

类推可得到i时刻系统状态变量与i，i+1，…，i+j-1时刻的状态预测，并代入新息形式的状态空间模型式(3)，可得到系统i时刻与0，1，…，i-1时刻的输出。

Γi=[CCA…CAi-1]T

由此得到构造的Hankel矩阵Yp，Yf以及Ep，Ef，下标p和f分别表示过去和将来相对时间的概念：

Yp=ΓiXp+HiUp+GiEp

(5)

(6)

Yf=ΓiXf+HiUf+GiEf

(7)

2.2 基于正交投影的闭环子空间辨识方法

CSOPIM辨识方法是基于正交投影的辨识方法，从控制对象的输入输出着手辨识对象模型，通过正交投影将输入输出数据转化为卡尔曼状态序列，再求出系统矩阵[6]。关键是引入了包含设定值Hankel矩阵的辅助变量。

2.2.1 基于正交投影的子空间辨识方法

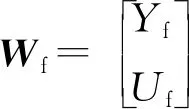
(8)

对Z进行SVD分解如下：

(9)

理论上Z的秩应该为nui+n，所以根据上述SVD分解结果进行阶次判定。

根据式(9)可知Z的正交补空间为U2。取M为单位矩阵，矩阵U2M可分解为U2M=(P1P2)T，简单变形得到：

(10)

但是上述方法用于系统闭环辨识效果并不理想，一种可行的解决方法是引入包含设定值Hankel矩阵的辅助变量[8]：

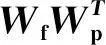
(11)

需要指出的是，辅助变量的构造方法并不是唯一的。

2.2.2 系统矩阵的计算方法

卡尔曼滤波状态可根据式(12)计算得到：

(12)

(13)

根据式(13)可求出Hi1，并构造出Hi。

定义：Rf=Ri+1|2i-1Up=U0|iYp=Y0|i

Uf=Ui+1|2i-1Yf=Yi+1|2i-1，从而得到：

(14)

式(14)中，Γi为Γi去掉最后ny行得到，Hi由Hi去掉最后ny行与nu列得到。

系统的参数矩阵A，B，C，K可根据以下公式求解得到：

(15)

但是该方法在闭环系统中应用效果可能不理想，由于反馈控制律的存在，Ui|i可能与Xi相关，从而导致有偏估计问题。为了解决这一问题，可以通过下述步骤求解：

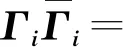
2)假定系统的参数矩阵中D=0；

3)参数矩阵B与K可以通过下式求解：

(16)

2.3 基于新息估计的闭环子空间辨识方法

在闭环辨识环境下，未来输入与过去噪声是相关的，使得正交投影不能消除噪声项，所以基于正交投影的子空间辨识在闭环下会存在有偏估计。而基于新息估计的闭环子空间辨识方法(PARSIME)的基本思想为由上一行的估计新息序列结果带到下一行中，下一行估计得到的值继续应用到后面的一行，即PARSIME算法从第一行块中估计新息序列，然后认为是已知新息去估计其它模型参数。

2.3.1 基于新息估计的子空间辨识方法

闭环子空间辨识与开环子空间辨识最大的不同在于未来输入数据与过去噪声数据存在相关性，故需要先将相关性消除，然后再进行无偏差辨识。在PARSIME方法中考虑将Hankel矩阵Yf按行分块：

Yf=[Yf1Yf2…Yfi…Yff]T，i=1，…，f

(17)

采用2.1节中类似的方法，得到如下的矩阵等式：

(18)

式(18)中，

Γfi=CAi-1

Hfi=[CAi-2B…CBD]≜[Hi-1…H1H0]

Gfi=[CAi-2K…CKI]≜[Gi-1…G1G0]

(19)

每一行需要计算Efi的估计值，计算如下：

(20)

当i=1时有：

(21)

(22)

因为新息序列已经得到估计值替代原始数据，故未来输入数据不再与新息序列相关，直接使用最小二乘求解。

借鉴其它子空间辨识方法，可确定权矩阵如下[9]：

(23)

(24)

2.3.2 系统矩阵的计算

关于系统矩阵的计算，根据上述计算结果重构系统状态，再进行系统矩阵的计算[10]。其具体计算步骤如下：

4)计算系统参数矩阵A，B与K，用MATLAB矩阵形式表示如下：

(25)

PARSIME方法将整体辨识模型分解为若干子模型，通过对子模型进行多步计算，避免了回归框架中对冗余非因果参数的重复估计，同时对新息模型计算得到新息估计值来代替系统噪声估计值，消除噪声的影响，解决了基于正交投影的闭环子空间辨识方法的有偏估计问题。

3 脱硫系统的闭环子空间辨识

3.1 闭环数据生成

针对某脱硫系统的传递函数模型[11]式(26)，采用基于扩增状态空间模型的预测控制器对该模型进行控制，生成闭环数据的预测控制器参数见表1。

(26)

式(26)中，pH表示浆液的pH值；SO2表示出口的SO2浓度，10-6；Q表示石灰石供给泵转速，r/min；L表示浆液循环泵电机频率，Hz。

以脱硫系统某运行平衡点为基准，令pH和SO2设定值按方波形式变化，同时在输入和输出变量上叠加白噪声信号，以模拟测量噪声，闭环数据生成相关参数见表2。仿真时间为15 000 s，最终生成的闭环输入和输出数据如图2与图3所示。

表1 生成闭环数据的预测控制器参数

图2 生成的闭环输入数据

图3 生成的闭环输出数据

3.2 闭环子空间辨识

3.2.1 辨识结果

分别采用CSOPIM与PARSIME辨识方法，计算得到的状态空间模型的系统矩阵如下：

CSOPIM方法的辨识结果：

PARSIME方法的辨识结果：

3.2.2 数据拟合效果对比分析

将两种闭环子空间辨识方法CSOPIM和PARSIME以及开环子空间辨识方法N4SID，与原始闭环数据的拟合效果进行对比，基于闭环数据的三种辨识方法辨识效果比较如图4所示。将每种辨识方法得到的两个输出量分别与原始闭环数据作差，得到输出量的误差，再计算输出量的绝对误差平均值与误差标准差，基于闭环数据的三种辨识方法的辨识效果比较指标见表3。由图表可知，闭环子空间辨识方法的效果总体比开环子空间辨识方法好，PARSIME方法的辨识效果优于CSOPIM方法。

表3 基于闭环数据的三种辨识方法的辨识效果比较指标

从理论角度来说，N4SID方法适用于开环数据的辨识，且易受干扰影响，因此N4SID方法用于闭环辨识效果不好。CSOPIM方法虽然属于闭环辨识方法，但是由于正交投影无法消除噪声项的影响，存在有偏估计的问题，而PARSIME方法通过将未知新息序列视为已知参数，从而能够得到系统参数的一致估计值，通过估计值来代替系统噪声估计值，以消除噪声的影响。因此PARSIME方法的辨识效果会更好。

图4 基于闭环数据的三种辨识方法辨识效果比较

3.2.3 阶跃响应对比分析

以表2中平衡点为基准，对石灰石供给泵转速做+1 r/min的阶跃，保持浆液循环泵频率不变，石灰石供给泵阶跃响应曲线比较图如图5所示；另外对浆液循环泵频率做+1Hz的阶跃，保持石灰石供给泵转速不变，浆液循环泵阶跃响应曲线比较如图6所示。

综合分析图4、图5和图6可知，不管是从数据拟合效果，还是从阶跃响应曲线，对于闭环数据而言，闭环子空间辨识方法的效果都比开环子空间辨识方法好，同时PARSIME方法的辨识效果优于CSOPIM方法。

图5 石灰石供给泵阶跃响应曲线比较

图6 浆液循环泵阶跃响应曲线比较

3.3 模型动态特性分析

分析图5可知，当石灰石供浆量增大时，由于新增的石灰石的溶解，浆液pH开始增大，同时吸收塔出口SO2浓度开始降低。当石灰石溶解速率与SO2吸收速率相等时，系统达到新的稳定状态。两者的变化方向相反，都属于大惯性和有自平衡能力的被控对象，其上升时间达3 000 s左右。

分析图6可知，当浆液循环流量发生阶跃变化时，由于液气比增加，烟气中更多的SO2被捕获，因此浆液pH和出口SO2浓度同时减小。pH的减小由离子液体相的缓冲能力阻止，并且随着浆液中石灰石的逐渐溶解pH降低幅度慢慢减小。因为SO2的吸收速率大于石灰石溶解速率，所以离子液体相的缓冲能力耗尽，pH继续减小。SO2吸收速率随之降低，石灰石溶解速率提高。当两者速率相等时，系统达到新的平衡。两者都属于大惯性和有自平衡能力的被控对象，但浆液循环流量变化对pH的影响明显快于对SO2浓度的影响。

通过分析，对湿法脱硫系统的主要动态特性总结如下：

1)由于脱硫系统的石灰石溶解速率低，出口SO2浓度和浆液pH的动态特性较慢。因此，需要在控制器设计中考虑输出预测和动态超调等措施，以改善系统的调节品质。

2)浆液循环流量变化对出口SO2浓度的影响在初期比较明显，但是在低Ca/S(pH)比运行时，浆液循环流量变化对出口SO2浓度几乎没有影响。这就表明，脱硫系统SO2吸收能力主要取决于外部石灰石的供给。

4 结语

本文采用基于正交分解和基于新息估计两种典型的闭环子空间辨识方法，建立了脱硫系统的状态空间模型，并对其有效性进行了对比分析。通过将两种闭环子空间辨识方法的辨识效果与开环子空间辨识方法N4SID进行对比，验证了闭环子空间辨识方法的有效性。同时通过理论分析与辨识效果比较，发现以PARSIME方法建立的脱硫系统的动态数学模型精度优于CSOPIM方法。此外，本文对湿法脱硫系统主要动态特性做出总结，为脱硫系统先进控制策略的研究奠定基础。