考虑车速的车辙预估模型研究
2021-03-01史春华
史春华
[上海市政工程设计研究总院(集团)有限公司,上海市 200092]
0 引 言
我国海南地区地处热带附近,夏季路面温度长期处于较高状态,再加上公路运输交通量的迅猛增长,给其高等级公路路面带来了日益严重的荷载考验[1]。海南地区严苛的气候条件对路面材料,尤其是直接承受荷载的沥青混凝土面层材料提出了更高的要求。
目前,早期建成通车的高等级公路上出现了较大面积的损坏,其中以车辙为主的高温稳定性病害占多数。路面车辙病害的研究是路面材料选择以及设计所关注的重点。在此前的研究中,车辙预估模型的形式已基本确定,但在应用中,发现由预估模型得到的结论与路面实际反应存在着较大差距,其主要原因在于传统的预估模型未能定量考虑不同车速对路面车辙的影响,其回归系数并不能很好反映路面对不同车速下荷载的响应[2-3]。
本文借助同济大学实验室的小型加速加载仪MMLS 3,进行了5 种车速下的沥青混合料车辙试验,并结合参考文献中的环道试验数据[4-6],对车辙预估模型中各因子的系数重新进行回归分析,进而对现行车辙预估模型提出改进。在传统模型的基础上增加车速因子,使其能更加准确地反映车辙形成与交通流之间的关系。
1 修正车辙预估模型简介
前期研究表明,沥青路面永久变形与温度、剪应力、抗剪强度以及轮载作用次数有关。相关研究[7-8]考虑到永久变形曲线的线性特征,综合考虑温度、剪应力、抗剪强度、荷载作用次数与永久变形的关系,得出永久变形预估模型的公式,如式(1)所示。

式中:RD为沥青层永久变形,mm;α,β,λ,η 为待定模型参数;n 为路面结构分层数;Ti为第i 亚层平均温度,℃;τi为第i 亚层平均剪应力,MPa;[τ]i为第i亚层抗剪强度,MPa;N 为轴载作用次数。
由于等效温度T 及剪应力τ 均随深度显著变化,为了提高预估模型的准确性,该模型引入分层叠加的思想,将沥青混合料层细分为若干亚层,分别计算各亚层的变形量。在确定亚层厚度时,需要同时考虑模型的精度及其简洁性,本文选取亚层厚度为1 cm。
各亚层的剪应力用Ansys 建模计算,建模时采用的模量统一为路面材料在20 ℃时的实测抗压回弹模量。模型已考虑了温度对永久变形的影响,在建模计算剪应力时不再重复考虑。
由于环道试验与室内轮辙试验均不能改变轮载的行驶速度,式(1)并不能体现车速对沥青层永久变形的影响。但实际上,不同车速情况下荷载对路面的损坏程度是不同的。考虑到车速与车辙深度成反比[9],由此提出一个修正的变形预估模型,如式(2)所示。
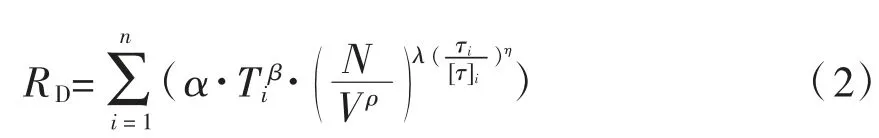
式中:V 为车速,km/h;ρ 为待定模型参数。
小型加速加载仪MMLS 3 能够变换车速进行试验。因此本文在前人研究成果的基础上,通过加速加载试验对车辙预估模型中车速因子的系数进行修正。
2 MMLS 3 加速加载试验
小型加速加载仪MMLS 3(见图1)具有操作方便,精确度高的特点,具有独立的温控系统、加载控制系统和荷载变形读取系统,加载对象为经过切割的旋转压实试件。加载试件如图2 所示。

图1 小型加速加载MMLS 3 试验机

图2 试件
2.1 试验方案
为了能够获得不同级配试件的测试结果,本文试验中选用了SMA13、Superpave13 和AC13 这3 种级配。另外,由于相同类型混合料的不同高度试件具有不同的剪应力分布,将每种类型的混合料试件切割成3 种高度。这样每9 个试件为1 组,可涵盖不同级配与不同高度。在试件下部垫上特制的金属垫片,以使不同高度试件的上表面基本平齐。
MMLS 3 能够调整车速,但车速是以控制电机VS mini J7 的不同频率表示的。确定了5 种频率:8 Hz、18 Hz、28 Hz、38 Hz、48 Hz,用每种频率加载1组试件。在车辙预估模型中,车速V 的单位是km/h。因此,有必要测定不同频率对应的车速。测量方法为:先测定MMLS 3 两胶轮间的距离S(m),秒表记下轮载作用1 000 次所花的时间t(s),则车速V(km/h)可按式(3)计算:

经测定,频率8 Hz、18 Hz、28 Hz、38 Hz、48 Hz下对应的车速分别为1.5 km/h、3.4 km/h、5.4 km/h、7.3 km/h、9.3 km/h。
为了保持试验环境的稳定,同时让试件尽早破坏,控制试验温度为60 ℃。
2.2 车速对永久变形的影响
以轮迹带中点为观测点,测得各车速下不同高度不同材料试件的车辙深度如图3~图5 所示。
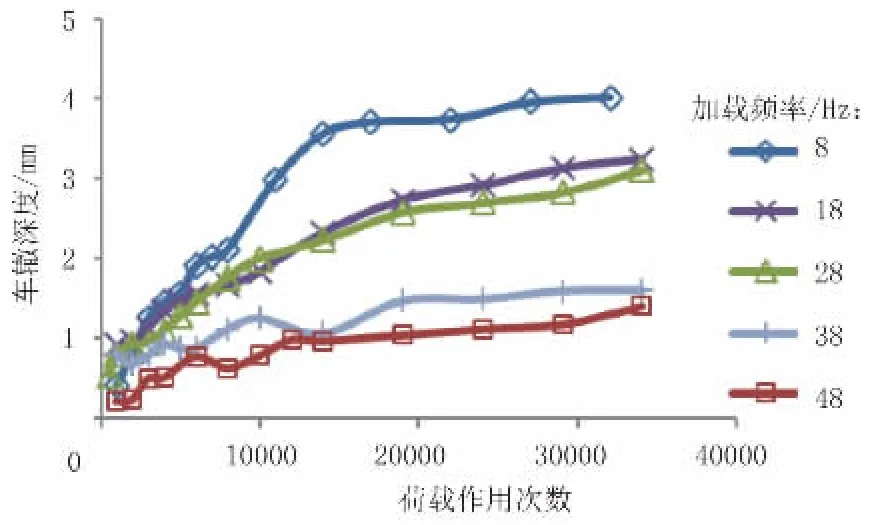
图3 S MA13 型沥青混合料试件在不同车速下的永久变形
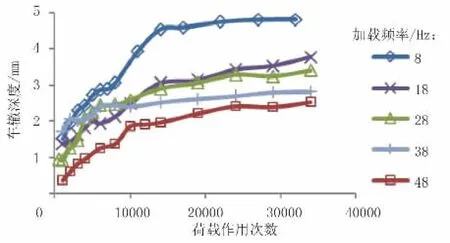
图4 S upe rpa ve 13 型沥青混合料试件在不同车速下的永久变形
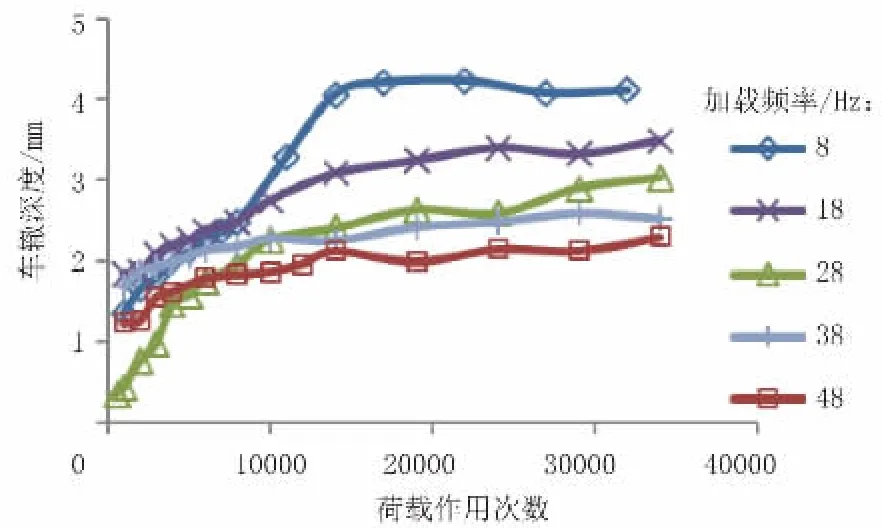
图5 AC13 型沥青混合料试件在不同车速下的永久变形
从图3~图5 可以明显看出,车速的变化对车辙深度的影响是显著的。沥青路面的车辙是塑性变形的积累,蠕变试验的规律很好地模拟了这一点。反映在实际行车荷载对路面结构的作用上,即为车速越慢,车辙越深。由加速加载试验中相同级配的车辙深度试验结果来看,显然随着车速的增大(加载频率的减小),同种类型混合料试件的变形趋向于减小。AC13 和Superpave13 型混合料试件的车辙深度随着荷载作用次数增多变化较大,而SMA13 的变形较小。当加载频率达到48 Hz 时,SMA13 的车辙深度变化最小。
由图3~图5 还可看出,在加载前期(荷载作用次数小于15 000 次),混合料变形还处于压密阶段,车辙深度增长明显;荷载次数大于15 000 次后进入加载的中后期,车辙增加趋势逐渐变缓。在中后期,车速与车辙之间的关系非常明显,车速越大,车辙越小。
3 考虑行车速度的修正车辙预估模型
引用MMLS 3 及环道的试验数据,即可采用遗传算法回归出式(2)中各参数的系数,得出最终的车辙预估模型。通过自制Excel 表,使用前只要将变形、温度、剪应力、抗剪强度、车速及轴次输入数据库文件,在设定好参数后,点击主界面上的“程序计算”按钮,即开始进行计算。计算结束后,各参数会自动显示在“回归结果”一栏里。其中参数1、2、3、4、5 分别对应式(2)中的α、β、λ、η、ρ。将这几个参数代入式(2)中,即可得到车辙预估模型。
将全部的MMLS 3 试验数据导入程序,得出模型中的各参数,再用环道的试验数据对其进行修正,最终得出车辙预估模型。各参数的计算结果如表1 所示。将参数代入式(2),再加入隆起系数后得到式(4)。
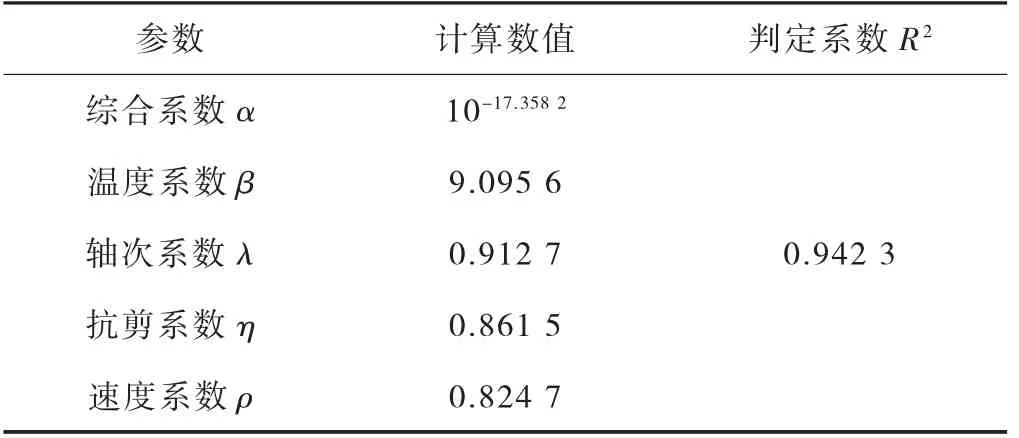
表1 模型参数计算结果表

式中:Lp为隆起系数,半刚性基层沥青路面取0.505,柔性基层沥青路面取0.33。
在设计过程中,目标路面结构需要通过永久变形量进行验算,因此构建预估模型将对设计人员提供重要的数据参考。在此之前,需要对模型进行真正的加速加载试验验证,环道试验即是众多加速加载试验之一。该试验能够真实模拟实际行车荷载,并在短期内达到较高的荷载作用次数[10]。因此,为了进一步模拟实际沥青路面永久变形规律,本节拟利用现有的环道加速加载试验数据[4-6]来参与修正车辙预估模型。
用式(4)估算环道试验中路面结构车辙,并通过与实测值比较得到修正系数a,再使用a 来修正车辙预估模型。实测值与预估值的计算结果对比见表2,并作图于图6 中。表2 和图6 中所述结构A、B、C 分别对应由SMA13、Superpave13 和AC13 所铺筑的上面层结构。

表2 环道车辙的预估值和实测值 单位:mm

图6 环道车辙的预估值和实测值
由图6 可知,结构A(即SMA13 上面层)的修正系数a(即纵坐标取值除以横坐标取值)为1.107,实测值与预估值的相关系数R2=0.947;结构B(即Superpave13 上面层) 的修正系数a 为1.579,R2=0.937;结构C(即AC13 上面层)的修正系数a为0.594,R2=0.928。由此可见,考虑了车速影响的修正后车辙预估模型与实际车辙数据具有很好的一致性。
4 结 语
(1)车速对沥青混合料永久变形的影响是显著的。保持其他试验条件不变,车速越小,沥青混合料最终形成的永久变形越大。
(2)考虑车速的车辙预估模型更加完善和精确。在车辙试验加载前期(荷载作用次数小于15 000次),混合料变形还处于压密阶段,车辙深度增长明显;荷载次数大于15 000 次后进入加载的中后期,车辙增加趋势逐渐放缓。在中后期,车速与车辙之间的对应关系更加明显。
(3)经过环道数据修正后的车辙预估模型预测效果优秀,采用修正后的模型对A、B、C 这3 种结构进行车辙预估,通过回归拟合的预估值与现场实测值的相关系数R2可分别达到0.947、0.937 和0.928。修正后新模型的预估精度高于之前未充分考虑车速的模型。此模型可在路面结构设计中提供重要参考。
