钢结构人行桥自振频率影响因素及其分析

叶 涛，李亚平，肖海波

（1.宁波市城建设计研究院有限公司，浙江 宁波315012；2.宁波市供排水集团有限公司工程建设管理分公司，浙江 宁波315041）

0 引 言

随着城市化进程不断发展，人行过街天桥及公园内景观天桥越来越多。伴随着人们日渐提高的审美，新时期的人行天桥与传统相比更加轻柔。由此带来结构固有频率的降低，使其易落入行人的正常行走步频范围内，引发人- 桥共振，使人行桥发生大幅度振动[1]。目前国内外人行桥规范对人行桥共振问题提出的设计基本方法主要有频率调整法和动力响应分析法两种。我国《城市人行天桥与人行地道技术规范》（CJJ 69—1995） 即采用频率调整法，即要求竖向自振频率不应小于3 Hz。人行天桥的过度振动不仅会给行人带来舒适性问题，而且对结构安全也有一定影响。故有必要对人行天桥的竖向振动特性及其影响因素进行深入研究。

1 影响桥梁自振频率的因素

用能量法近似求解结构的自振频率公式如下：

式中：ω 为圆频率；f 为频率；E 为材料弹性模量；I为截面惯性矩；Y（x）为位移形状函数；Yi为质点mi的振幅为平均质量；l 为桥梁跨度。

由式（1）、式（2）可知，桥梁的自振频率与以下因素有关：

（1）桥梁结构型式。结构型式不同，位移函数Y（x）就不同，从而影响结构的自振频率。

2 计算分析

2.1 计算模型

本文通过有限元软件Midas Civil 2019，采用梁单元进行全桥模拟计算。其中计算截面采用钢箱梁，由于主要分析动力效应，故将自重和二期恒载转化为质量参与计算，分析类型采用子空间迭代[2]。钢箱梁截面尺寸如图1 所示。

图1 钢箱梁截面示意图（单位：mm）

钢梁材质选用Q355D。

二期恒载的选取。钢桥面铺装采用设计中较常用的两种类型：①5 mm 厚聚脲防水涂料防滑层+ 金刚砂；②70 mm 厚的ERS。栏杆荷载采用单边2.5 kN/m。

2.2 计算结果

2.2.1 结构型式不同对自振频率的影响

在相同计算跨径30 m，同种铺装类型（ERS）下，在不同高跨比下不同边中跨比的等截面连续梁的频率对比见表1。

表1 不同边中跨比连续梁的频率值 单位：Hz

由计算结果可得，相同条件下，连续梁的边中跨比越小，结构的自振频率越大。这是由于连续梁的边跨对中跨有一定的约束作用，导致计算跨径的位移函数Y（x）产生了变化，而边中跨比越小，约束作用越强。

在相同计算跨径30 m，同种铺装类型（ERS）下，在不同高跨比下简支梁与等截面连续梁（表中边中跨比取0.65）的频率对比见表2。

表2 简支梁与连续梁的频率值 单位：Hz

由计算结果可得，相同条件下，由于边跨的约束作用，连续梁比简支梁自振频率要高出约39%。由表1 跟表2 的数据可知，当连续梁的边中跨比为1 时，其自振频率同相同计算跨径下的简支梁。

在相同计算跨径40 m，边中跨比取0.65，同种铺装类型（ERS）下，进行等截面连续梁（h=1.6 m）与变截面连续梁（h=1.2～2.4 m）的频率对比。在保证总的用钢梁一定的情况下，得到如图2、图3 所示结果。

图2 等截面连续梁竖向一阶频率图示

图3 变截面连续梁竖向一阶频率图示

由计算结果可得，相同条件下，等截面连续梁频率（3.4 Hz）大于变截面连续梁频率（3.0 Hz）。这是由于结构的跨中位移对频率影响最大，同样用钢梁下，变截面连续梁跨中梁高低、位移大。

2.2.2 高跨比不同对自振频率的影响

在同种铺装类型（ERS）下，简支梁在不同高跨比下的频率值如图4 所示。

图4 简支梁在不同高跨比下频率曲线（ERS）

由计算结果可得，相同条件下，梁高越高，频率越大。以规范规定的3 Hz 为极限频率，梁高为L/20时极限跨径可取到40 m，梁高为L/25 时极限跨径可取到30 m，梁高为L/30 时极限跨径可取到25 m，梁高为L/40 时极限跨径可取到20 m。

在同种铺装类型（聚脲+ 金刚砂）下，简支梁在不同高跨比下的频率值如图5 所示。

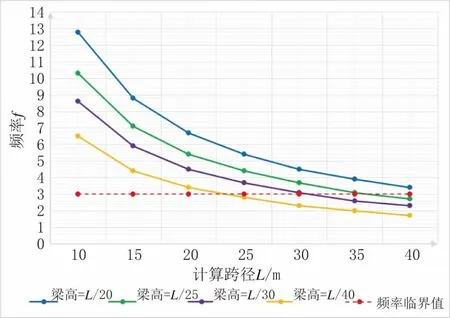
图5 简支梁在不同高跨比下频率曲线（聚脲+ 金刚砂）

由计算结果可得，相同条件下，梁高越高，频率越大。以规范规定的3 Hz 为极限频率，梁高为L/20时极限跨径可取到45 m，梁高为L/25 时极限跨径可取到35 m，梁高为L/30 时极限跨径可取到30 m，梁高为L/40 时极限跨径可取到25 m。

在同种铺装类型（ERS）下，连续梁（边中跨比取0.65）在不同高跨比下的频率值如图6 所示。

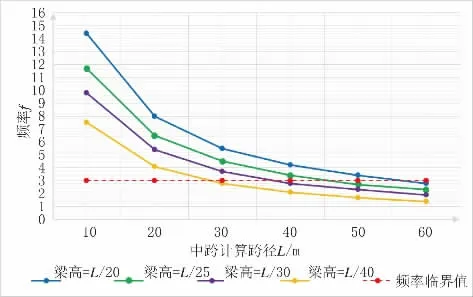
图6 连续梁在不同高跨比下频率曲线（ERS）

由计算结果可得，相同条件下，梁高越高，频率越大。以规范规定的3 Hz 为极限频率，梁高为L/20时极限跨径可取到55 m，梁高为L/25 时极限跨径可取到45 m，梁高为L/30 时极限跨径可取到35 m，梁高为L/40 时极限跨径可取到25 m。

在同种铺装类型（聚脲+ 金刚砂）下，连续梁（边中跨比取0.65）在不同高跨比下的频率值如图7 所示。

图7 连续梁在不同高跨比下频率曲线（聚脲+ 金刚砂）

由计算结果可得，相同条件下，梁高越高，频率越大。以规范规定的3 Hz 为极限频率，梁高为L/20时极限跨径可取到60 m，梁高为L/25 时极限跨径可取到50 m，梁高为L/30 时极限跨径可取到40 m，梁高为L/40 时极限跨径可取到30 m。

2.2.3 铺装不同对自振频率的影响

简支梁在相同高跨比（L/25），不同铺装类型下，结构频率值对比见表3。

表3 不同铺装类型简支梁的频率值 单位：Hz

由计算结果可得，相同条件下，铺装越薄，结构频率越大，5 mm 厚的聚脲+ 金刚砂比相同条件下的70 mm 厚的ERS 频率可增加约15.3%。

3 结 语

本文通过Midas Civil 2019 梁单元模型进行有限元分析计算，可得到以下结论：

（1）连续梁的边中跨比越小，结构的自振频率越大。当边中跨比为1 时，频率等于同等条件下的简支梁。设计中在满足边跨受压的情况下，可适当减少边中跨比。

（2）相同条件下，连续梁（边中跨比取0.65）比简支梁自振频率要高出约39%。

（3）相同条件下，且用钢量一定时，等截面连续梁频率大于变截面连续梁。

（4）梁高越高，频率越大；在不考虑结构强度、刚度及稳定性的情况下，理论给出了不同高跨比下简支结构及连续结构在不同铺装类型情况下满足3 Hz频率要求的极限跨径。

（5）铺装越薄，结构频率越大，5 mm 厚的聚脲+金刚砂比相同条件下的70 mm 厚的ERS 频率可增加约15.3%。