基于Bezier拟合的射线检测焊缝缺陷指数和峰谷指数的计算

2021-03-01党长营李建素曾志强杜文华

无损检测 2021年2期

党长营,李建素,曾志强,杜文华

(1. 中北大学机械工程学院，太原 030051; 2. 中北大学先进制造技术山西省重点实验室，太原 030051)

受射线检测图像的多样性和复杂性、缺陷识别的准确性等因素影响，射线检测的自动化和智能化仍处于理论研究阶段[1-2]。目前，自动缺陷识别系统在实际应用中的主要问题是精度低、可靠性低、效率低等，尤其是在对大量射线检测图像进行自动识别时，这些问题更为明显。

在自动射线检测中，缺陷探测的主要目的是判断射线检测图像中缺陷的存在性、位置、大小等,其为缺陷自动识别系统提供了主要的缺陷信息，如位置、灰度、形状等，对提高识别系统的精度和效率具有重要意义[3-4]。此外，要特别注意缺陷探测和缺陷分类的不同[5]，缺陷探测只用区分缺陷区域和非缺陷区域这2种情况；而缺陷分类则要识别缺陷具体属于哪一类缺陷，如气孔、夹渣、裂纹、未焊透、未熔合(即射线检测的5大类缺陷)等。

常见的缺陷探测方法有基于列灰度波形分析的探测[6]、基于特征提取的探测[7-8]、基于分割的探测[9-11]等，它们具有各自的特点、优势、适用性和局限性。

在前期研究中，为了解决常用缺陷探测方法存在的阈值和系数设置过多、有效特征提取困难、对噪声敏感、探测精度低、误报率高等问题，笔者曾提出一种射线检测图像中焊缝缺陷探测的新方法(ANDM)[12]。在该方法中，提出了焊缝缺陷指数(DI)和峰谷指数(PVI)的概念，并对其进行了定义；同时，利用这两个指数实现了焊缝缺陷的高精度、高效率和高可靠性探测。文章将系统地分析Bezier拟合的特点和作用、DI和PVI的定义及计算方法，以进一步论述Bezier拟合对DI和PVI的重要性和影响特性。

1 相关理论

ANDM的算法原理如图1所示，其主要由感兴趣区域(Region of interest, ROI)提取、Bezier曲线拟合和基于DI和PVI的缺陷判别3部分构成。由图1可以看出，Bezier曲线拟合不仅是DI和PVI计算的基础，而且是ANDM的核心环节之一。因此，Bezier拟合对DI和PVI的计算，以及ANDM的性能具有至关重要的影响。

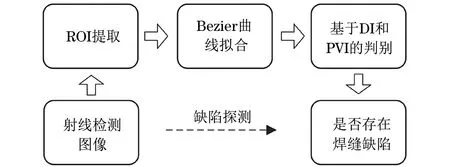
图1 ANDM的算法原理

1.1 Bezier拟合的特点和作用

理论上，如果一个ROI图像中没有缺陷，则所有横穿过焊缝的列灰度轮廓将表现为具有一定局部波动的钟形分布；相反地，如果存在缺陷，它将破坏该钟形分布，并导致局部发生畸变。因此，通过搜索灰度列轮廓的局部畸变，可以实现对ROI图像中缺陷的探测和定位。然而实际上，受射线图像的噪声和低对比度等因素的影响，要辨别局部畸变是由缺陷引起的，还是由其他因素引起的是非常困难的。针对此问题，前期研究中提出采用Bezier拟合来排除局部波动和由非缺陷因素引起的畸变。

Bezier曲线是指用光滑参数曲线段逼近一个折线多边形，其不要求给出导数，只要给出数据点就可以构造曲线，而且曲线的阶次严格依赖该段曲线的数据点个数。Bezier函数实质上是一个多项式函数，其形状可以通过数据点(即控制点)的位置直观地确定，并且包括全局形状信息[13]。Bezier函数能非常容易地合并和有效地追踪规则或变化莫测的数据点，具有极好的协调和平滑特性。特别地，在利用Bezier函数对数据进行分析时，有3个重要的特性：原始数据的均值和拟合数据的均值是一样的；高阶多项式拟合不会存在局部畸变；相关和非相关变量在用Bezier函数表达时可去耦合关系。

一个n阶Bezier曲线P(u) 可以通过n+1个控制点来确定，即

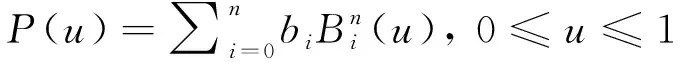
(1)

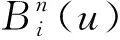
其中，Bernstein多项式可表示为

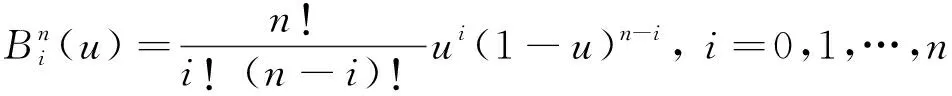
(2)

Bezier曲线的一个重要特征是逼近曲线必然经过逼近数据的起始点和终点，即有

P(0)=b0;P(n)=bn

(3)

式中：b0为数据的起点坐标；bn为数据的终点坐标。

此外，多项式P(u)的Bezier坐标b′i是多项式P(u)的导数，其可表示为

b′i=n(bi+1-bi),i=0,1,…,n-1

(4)

1.2 DI和PVI的定义及计算方法

为了对列灰度轮廓的钟形分布和缺陷引起的局部畸变进行精确描述，前期研究提出了DI和PVI的概念，并对其进行了定义。

PVI是对Bezier拟合曲线钟形的度量，其为列灰度轮廓的Bezier拟合曲线中峰值点和谷值点个数的总和，可表示为

PVI=NP+NV

(5)

式中：PVI为PVI的值；NP为峰值点个数；NV为谷值点个数。

DI是描述缺陷存在性的度量，可以通过Bezier拟合曲线的拟合误差AE得到，可表示为

(6)

式中：DI为DI的值；M(AE)为|AE|的最大值；σ为|AE|的标准差；μ为|AE|的均值；c2为图像的质量系数。

其中，拟合误差AE可表示为

AE=PA(i)-P0(i),i=1,2,…,WR

(7)

式中：PA(i)为Bezier拟合曲线；P0(i)为原始列灰度轮廓曲线；WR为ROI区域宽度。

由于列灰度轮廓的钟形特性和缺陷引起的局部畸变特性，可通过DI和PVI对Bezier拟合曲线的钟形特性和局部畸变进行度量，以达到有效判别缺陷存在性。如果列灰度轮廓穿过焊缝ROI的缺陷，则有

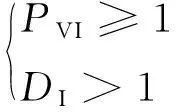
(8)

通过式(8)可以实现对射线检测图像中的5大类焊缝缺陷的高精度和高可靠性探测。

2 试验与分析

为了进一步论证Bezier拟合对DI和PVI的重要性和影响特性，下面将开展不同方法的拟合对比试验和不同缺陷的DI和PVI计算对比试验。试验中，射线检测的对象是大型燃气轮机主机关键部件的焊缝。

2.1 不同方法的拟合对比试验

为了证明Bezier方法在拟合穿过焊缝ROI缺陷的列灰度轮廓时是至关重要的，将其与最小二乘多项式拟合和高次样条拟合进行了对比试验。

特别地，由于高次多项式和高次样条拟合不仅会带来计算上困难，而且容易导致“龙格(Runge)效应”，因此，在实际使用中，其阶数一般不超过10次。试验选择了拟合效果比较好的10次多项式拟合和10次样条拟合与Bezier拟合进行对比，以说明Bezier拟合的有效性和优势。

焊缝缺陷在射线检测图像上往往呈现出高灰度或低灰度，故部分试验采用了具有代表性的气孔图像(468像素×453像素)、裂纹图像(552像素×524像素)和夹钨图像(445像素×443像素),不同方法拟合line1列位置灰度轮廓的曲线分别如图24所示(灰度值无量纲),图像的像素当量均为50 μm，选择的line1列刚好穿过上述缺陷，缺陷沿line1方向的长度分别约为3.5，1.5,1.15 mm。

由图2(b)图4(b)可以很明显看出，Bezier拟合曲线与10次多项式拟合曲线和10次样条拟合曲线存在非常大的差异。10次多项式拟合不能有效地描述原始数据的轮廓趋势，特别是在图2(b)中，line1列轮廓穿过2个气孔缺陷，灰度轮廓存在2个明显的波谷畸变时，10次多项式拟合曲线完全不能反映原始数据点的原有趋势，并且出现了一定的“龙格效应”。此外，因为拟合曲线的趋势是未知的，所以10次多项式拟合的阶数很难确定。10次样条拟合曲线虽然能一定程度上反映缺陷引起的局部畸变和原始数据的基本趋势，但其分段拟合的段数和拟合的次数难以确定，且存在严重的“龙格效应”，特别是当拟合的段数过多、拟合的次数较大时，其基本上是将所有数据点平滑的串联起来，这样不能达到滤除噪声的目的；拟合的段数过少、拟合的次数过小时，又不能有效反映原始数据的走势，不能获得期望的曲线效果。Bezier拟合曲线不仅能够有效描述原始数据点的趋势，而且可有效反映缺陷引起的局部畸变，获得期望的拟合曲线。这主要是因为Bezier曲线中的每个控制点都会影响整个曲线的形状，并且其能够根据原始数据点自适应地确定拟合的阶数，因此，其在滤除原始数据噪声的同时，还能够有效反映原始数据的局部畸变。这正是Bezier拟合对DI和PVI重要性的体现。

图2 气孔图像line1列位置及其不同方法的灰度轮廓拟合曲线

图3 裂纹图像line1列位置及其不同方法的灰度轮廓拟合曲线

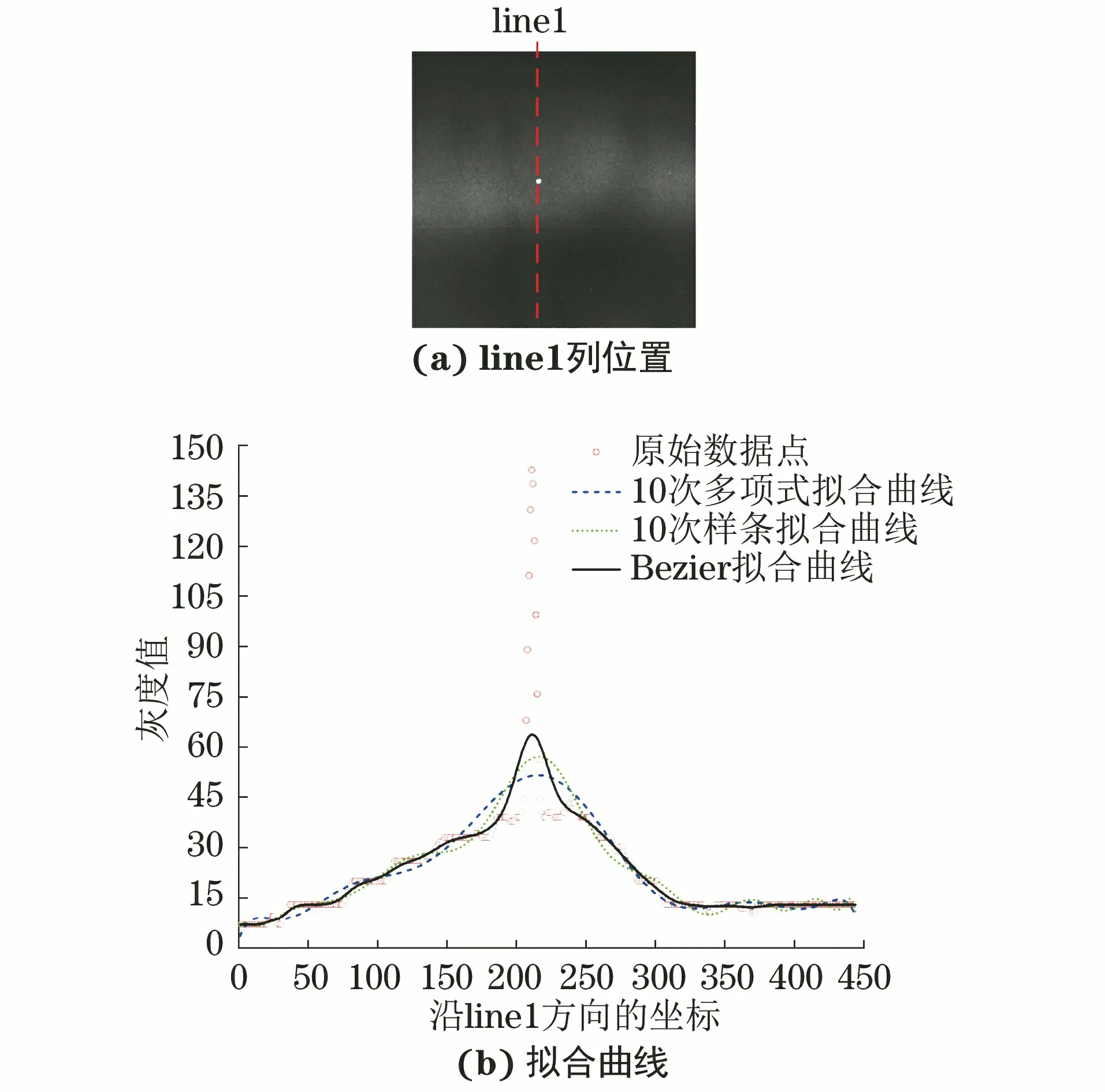
图4 夹钨图像line1列位置及其不同方法的灰度轮廓拟合曲线

2.2 不同缺陷的DI和PVI计算对比试验

为了论证Bezier拟合对DI和PVI的影响特性，分别对上述具有代表性的气孔、裂纹、夹钨等缺陷的缺陷列和非缺陷列的DI和PVI进行计算对比试验。

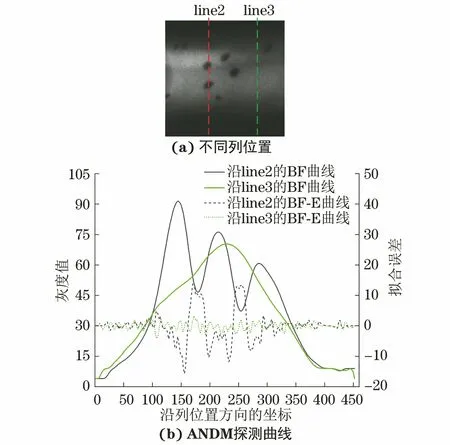
图5 气孔缺陷的不同列位置及其ANDM探测曲线

图6 裂纹缺陷的不同列位置及其ANDM探测曲线

图7 夹钨缺陷的不同列位置及其ANDM探测曲线

针对上述不同类型的缺陷，穿过缺陷区域的line2位置和穿过非缺陷区域的line3位置以及沿这两条列灰度轮廓的Bezier拟合曲线(BF曲线)和拟合误差曲线(BF-E曲线)分别如图57所示(拟合误差为灰度差值，无量纲)，BF曲线和BF-E曲线又称为缺陷的ANDM探测曲线。从图5(b)7(b)可以明显看出，沿line2的BF曲线含有缺陷引起的局部畸变，且列轮廓的钟形分布遭到破坏；其对应的BF-E曲线也表现出非常剧烈的波动。最重要的是，BF曲线畸变的程度和BF-E曲线波动的幅度也会根据不同的缺陷自适应地变化，BF曲线和BF-E曲线可以有效反映缺陷的存在性。此外，沿line3的BF曲线具有相对完整的钟形形状，虽然可能存在一定程度的微小波动，但不存在局部畸变；并且它们对应的BF-E曲线不存在大的波动，且幅度明显很小，即非缺陷因素不会引起BF曲线的局部畸变和BF-E曲线大幅度的波动。由于DI和PVI指数是基于BF曲线和BF-E曲线的特性分析获得，可有效描述BF曲线和BF-E曲线的变化，因此通过DI和PVI值的变化可有效探测缺陷的存在性。

根据DI和PVI的定义，分别计算上述图像中所有沿line2和line3列轮廓线的DI和PVI值，其计算结果如表1所示。

表1 沿line2和line3列灰度轮廓的DI和PVI值

从表1可以明显地看出，所有沿line2列轮廓的DI值均较大且大于1，而PVI值均大于等于1，即均满足式(8)关系，也就是说，通过判别DI和PVI的值，缺陷被成功地探测到；但是所有沿line3列轮廓的PVI值均为1，且其DI值均较小且小于1，即不满足式(8)关系，因此，可以判断line3列经过非缺陷区域。经过缺陷的line2列轮廓的DI值远远大于经过非缺陷的line3列轮廓的DI值，具体来说，经过气孔、裂纹和夹钨缺陷的line2列轮廓的DI值比不经过对应缺陷的line3列轮廓的DI值分别高出了3 016.00%，96 903.33%和169 904.35%。因此，在评估经过缺陷和非缺陷区域的列轮廓的差异时，DI值是非常有效的参数，其差别非常明显，容易辨别。

从上述试验结果可以看出，尽管缺陷的类型、大小及特点等存在非常大的差异，但是，DI和PVI指数仍能够非常容易和有效地判别出缺陷区域与非缺陷区域，这正是得益于Bezier拟合的特点和优势，因此Bezier拟合对DI和PVI至关重要，这也是DI和PVI概念和定义的精髓所在。