一种校园供水系统智能管理模型的构建

蒲宝卿，包 蕾，刘代娜

目前，城市供水企业为实现企业盈利、节能降耗等目标，已经将抄表催费、维修抢修、在线监控等各项业务工作逐步信息化、标准化，实现了智能化管理［1］.基于现代通讯技术和云计算的城市供水智能管理系统的构建，可有效整合各系统资源，从而实现供水系统各模块最大程度的共享，为供水系统科学管理提供决策支持［2］.

学校内部用水点及用水量的逐年增加，迫切需要校园供水系统实现智能化管理，智能水表的普及安装有助于校园后勤管理部门实时获取全面、准确的系统运行数据，基于此可以通过数据挖掘和数学建模技术优化校园供水系统，提升校园服务和管理水平.

1 校园不同功能区的用水规律特征分析

基于某校区水表层级关系以及所有水表四个季度的读数（以一定时间为间隔，如15 分钟）与相应的用水数据［3］，利用Matlab 软件首先对每块水表每天的小时用水量进行计算；然后对每块水表在每一季度内的小时平均用水量进行求解；最后作出每块水表在每一季度内的小时平均用水量随时间变化的曲线.部分水表数据变化曲线如图1 和图2 所示.

基于每块水表的编号及名称，结合每块水表的用水变化曲线将该校区划分为宿舍、食堂、教学、办公、后勤保障、文娱服务、绿化养殖7 个功能区，如表1 所示.

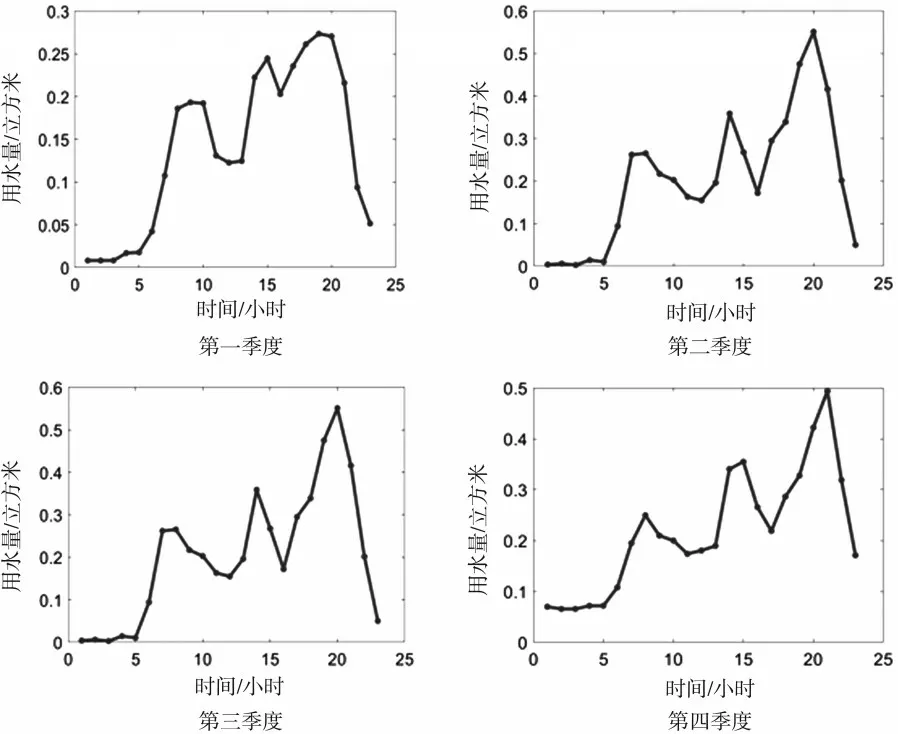
图1 某校区第五食堂水表数据变化规律图

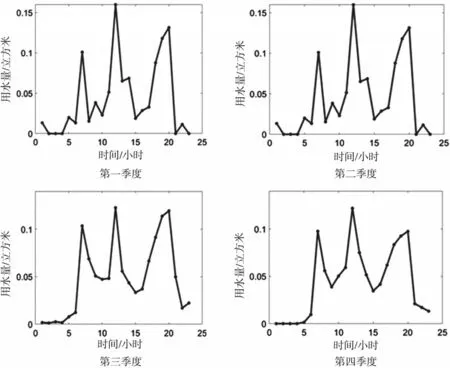
图2 物业水表数据变化规律图

功能区的划分主要遵循以下原则：名称相似的归为一个功能区；功能相似的归为一个功能区；工作性质相似的归为一个功能区；同属于一个大楼区域的水表属于同一个功能区；有些水表从名称上看不出功能，给予舍弃.一级总水表属于区域水表，不能划分到某一特定的功能区，给予舍弃.

1.1 宿舍功能区用水特征分析

宿舍功能区用水随时间和季度的变化趋势如图3 所示，从日用水量的变化趋势上看，宿舍功能区在6：00～9：00、20：00～23：00 用水量较大，2：00～6：00、15：00～19：00 用水量相对较小，这与学生的生活学习节奏相一致；不同季度中宿舍用水变化趋势一致，其中第一季度用水较少，第四季度用水最多.这受到学校寒暑假、冬天供暖等因素的影响.总之，宿舍功能区呈现出早晨晚上用水多、深夜和下午用水少、第四季度用水多、第一季度用水少的特征.

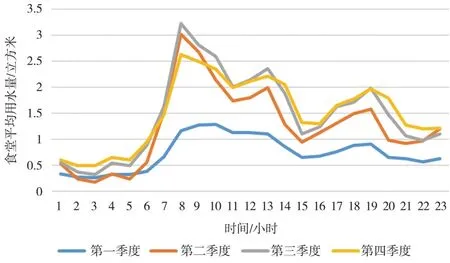
图3 宿舍功能区平均用水量的变化趋势图

表1 功能区划分明细

1.2 食堂功能区用水特征分析

食堂功能区用水随时间和季度的变化趋势如图4 所示，从日用水量的变化趋势上看，食堂功能区在6：00～15：00、17：00～20：00 用水量较大，1：00～6：00、20：00～23：00 用水量相对较小，这与学校一日三餐期间用水多、晚上和夜里不做饭而用水少的习惯相一致；不同季度中宿舍用水变化趋势一致，其中第一季度用水较少，其他季度用水较多且用水量差距小，这是因为第一季度包含寒假、学校食堂关闭.总之，食堂功能区呈现出白天三餐期间用水多、晚上深夜用水少、第一季度用水少、其他季度用水差距小的特征.

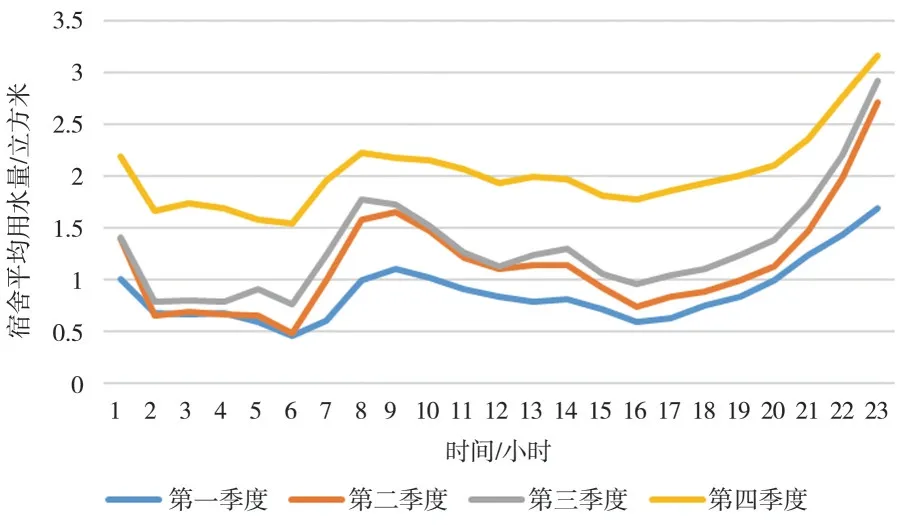
图4 食堂功能区平均用水量的变化趋势图

1.3 其余五个功能区的用水特征分析

教学功能区呈现出白天上课期间用水多、晚上深夜用水少、上午用水多于下午；第一季度用水少、第二季度用水较多的特征.

办公功能区呈现出白天办公期间用水多、晚上深夜用水少、上午用水多于下午；第一季度用水少、其他季度用水量差距小的特征.

后勤保障功能区呈现出全天24 小时用水、季度用水趋势一致、用水量差距小的特征.

文娱服务功能区呈现出白天和傍晚用水多、第三季度用水明显增多、游泳池对用水量影响较大的特征.

绿化养殖功能区呈现出全天多个用水高峰点、不同季节用水变化趋势差异大的特征.

2 水表数据关系模型的构建及误差分析

基于校区水表层级关系，分别统计一级水表、二级水表、三级水表的累积用水量，建立一级水表和二级水表的用水量关系对比模型、二级水表和三级水表用水量的关系对比模型.其中一级水表和二级水表用水量随时间的变化关系对比模型如图5、图6 所示.其中图5 时间间隔为15 分钟，图6 时间间隔为6小时.

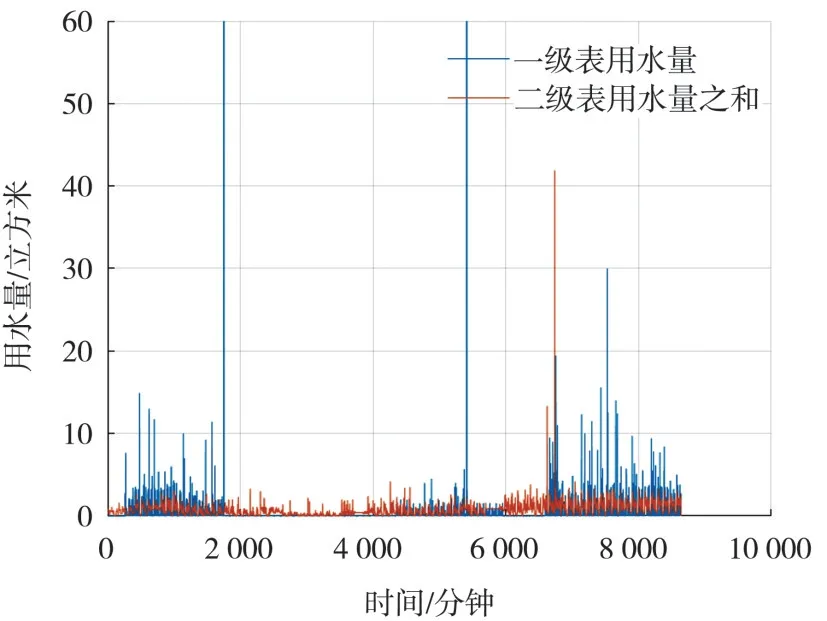
图5 一级水表和二级水表数据关系模型图

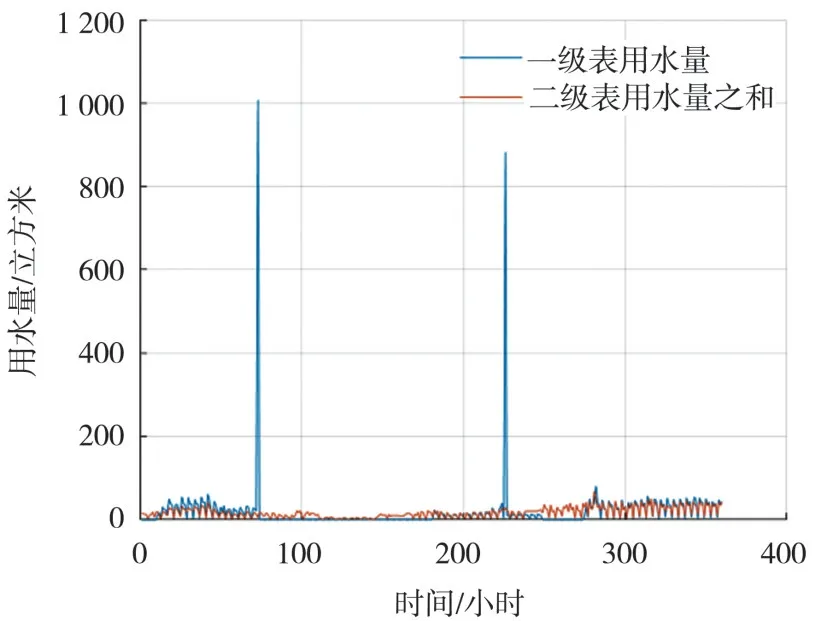
图6 一级水表和二级水表数据关系模型图

从图5、图6 可以看出，一级水表和二级水表曲线变化趋势基本吻合，但是在某些点一级水表数据有多个峰点.分析可能存在三个原因：一是由于管网泄漏造成；二是因为现实的供水管网由许多环路和支路共同组成，一级水表的供水不仅仅要供给其下游的二级水表和管网，还要供给整个管网中其他一级水表下的二级水表；三是由于水表时滞造成的读数误差；有时候二级水表用水量总和大于一级水表，这其中也包括三个原因：一是管道存水引起；二是因为供水管网环路中由其他的一级水表进行供给；三是由供水时滞造成的.

对于一级水表，401X、403X 和405X 水表下面有多个二级水表，且水表都有读数，而其他一级水表因为下面二级水表较少或者无记录，统计误差较大，所以只分析了一级水表401X、403X 和405X 与其二级水表的数据关系.同理，针对二级水表分析了40337X、40134X和40133X 与其三级水表的读数关系误差.

基于附件数据用Matlab 对要分析的水表的用水量进行统计，得出一级水表401X、403X和405X 与其二级水表数据关系模型如图7～图9 所示.这3 个图的时间间隔均为15 分钟.

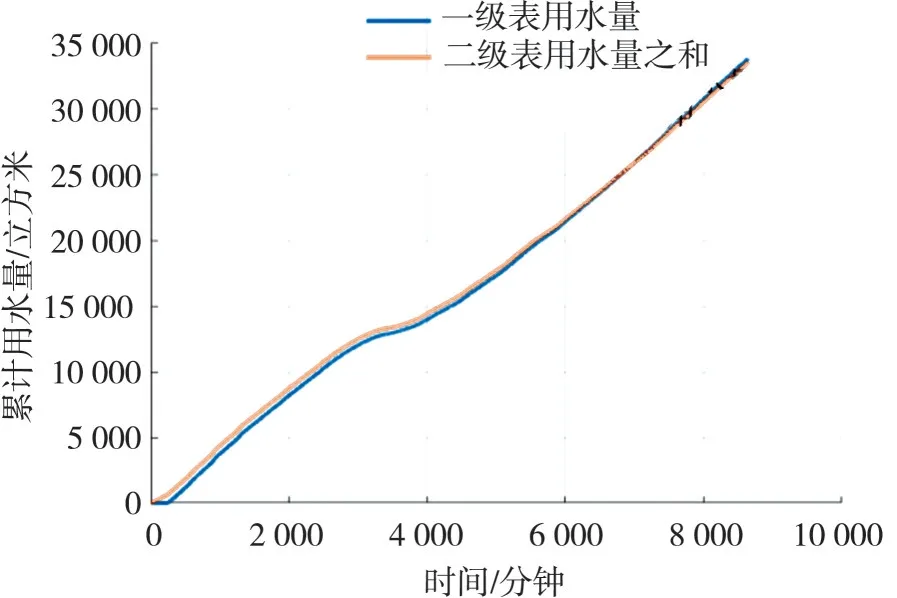
图7 一级水表401X 与其二级水表的数据对比模型

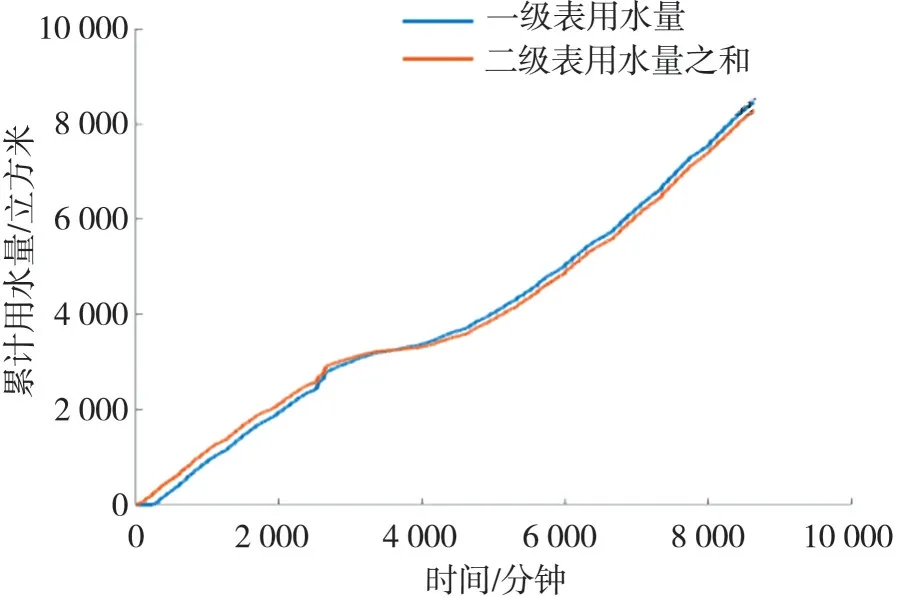
图8 一级水表403X 与其二级水表的数据对比模型

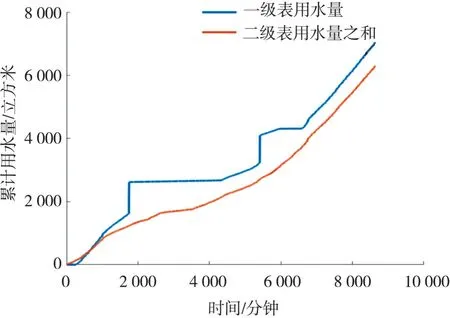
图9 一级水表405X 与其二级水表的数据对比模型

从图7～图9 可以看出，一级水表用水量和二级水表用水量变化趋势基本一致，当一级水表用水量低于二级水表用水量时，说明存在供水读数时滞、管网存水、以及环路中其他水表供水情况；当一级水表用水量大于二级水表用水量时，说明存在供水管网的漏损情况，如果差距小，说明管网属于正常供水损耗，如果差距较大，说明存在管道破裂、阀门松动等较为明显的漏损情况.经过统计计算，一级水表401X、403X 和405X 与其二级水表数据关系模型误差分别为1.81%、0.74%和10.62%.同 理，二 级 水 表40337X、40134X 和40133X 与其三级水表的读数关系对比模型如图10～图12 所示.这3 个图的时间间隔均为15分钟.

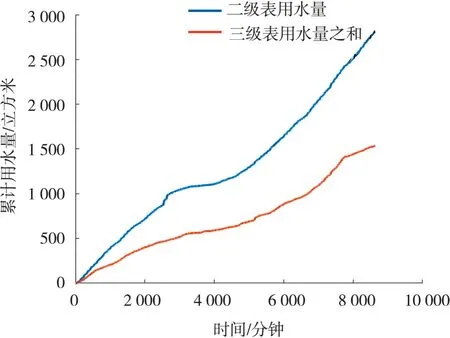
图10 二级水表40337X 与其三级水表的数据对比模型

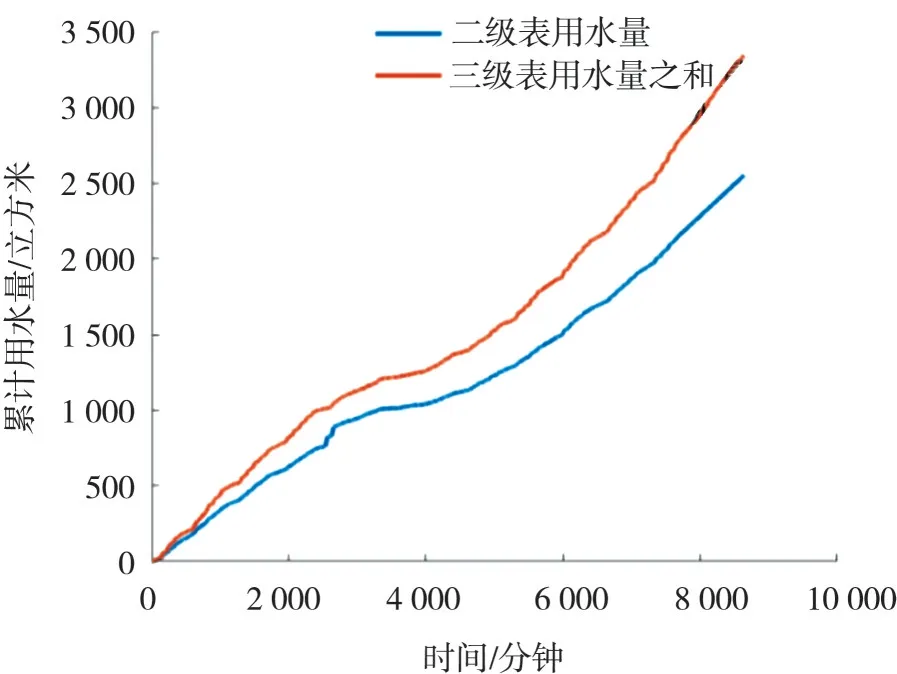
图11 二级水表40134X 与其三级水表的数据对比模型

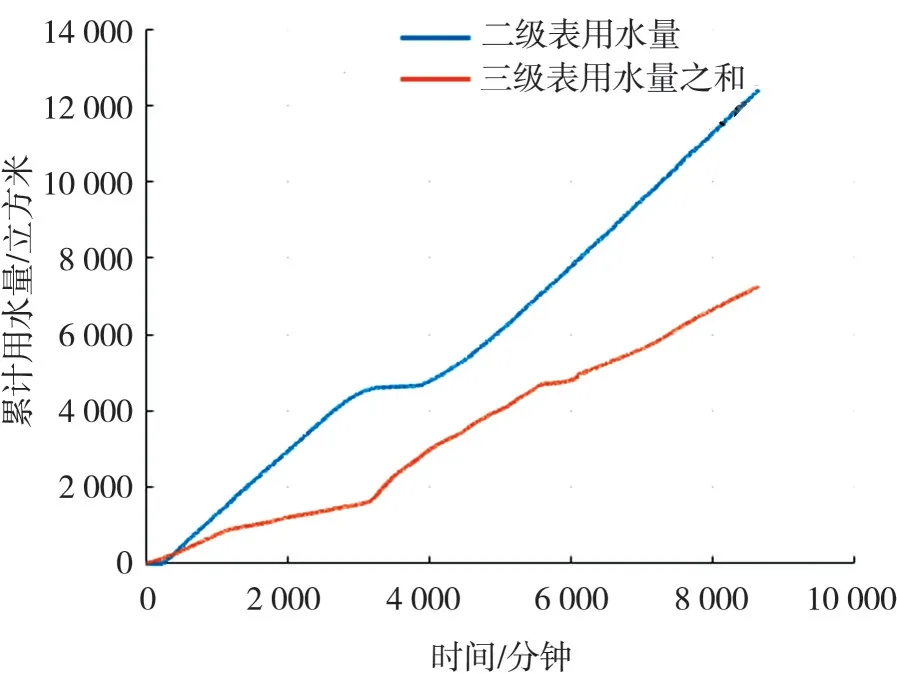
图12 二级水表40133X 与其三级水表的数据对比模型

从图10～图12 可以看出，二级水表用水量和三级水表用水量变化趋势基本一致，但是两者之间的读数差距较大，说明存在较强的读数时滞和漏水现象，这是因为水表和管道数量多，水表分布相对分散，有些管道甚至是老旧管网.经过统计计算，二级水表40337X、40134X 和40133X 与其三级水表数据关系模型误差分别为-23.67%、45.30%和41.41%.

3 供水管网漏损分析

如果不用水时，水表继续匀速转动，说明存在漏水现象；如果水表连续匀速转动，说明管网也存在漏水现象.针对该校区的每个水表数值，因为附件数据统计时间间隔为15 分钟，若连续12 条记录的用水量相同，也就是3个小时内某个水表转动均匀，那么判定相关的管网漏水.基于此模型，分别统计每个水表读数变化趋势，进而分析出整个供水管网的漏水比例如表2 所示.

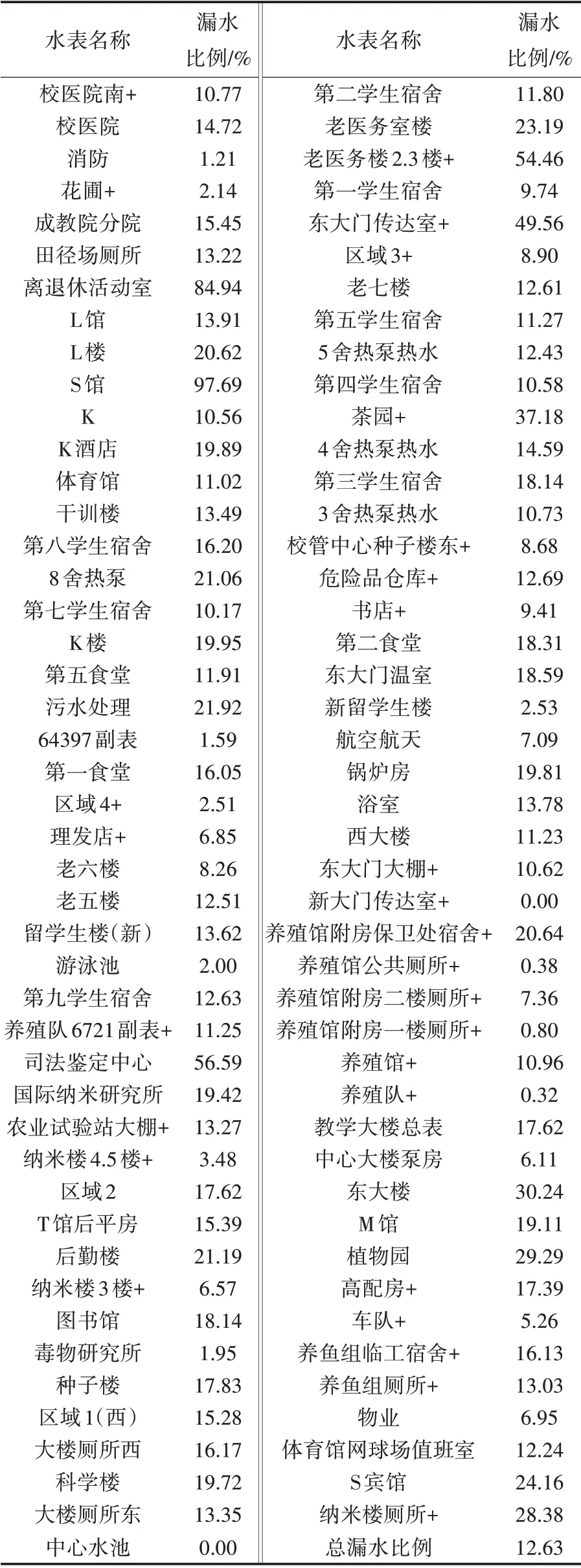
表2 校区内所有水表的读数变化情况及管网漏损情况

从表2 可以看出，不同水表反映的管网漏水情况差距较大，最高的漏水比例可达到90%以上，总漏水比例为12.63%，大于良好供水网络5%的标准，说明该校区的供水网络存在较大的漏损情况，需要进行漏损管网的检测、定位和维修.

漏损位置的确认主要是通过水表的实时数据规律确定.一般步骤如下：

Step 1：根据各级水表中实时的用水量数据规律，分辨哪个水表下的水管存在漏损情况.

Step 2：对每个存在漏损水管的水表判断是否存在下级水表同样有漏水情况，若存在，则继续找下一级水表，直到不存在为止.

Step 3：若找到最下级的漏水水表下不存在更低级的水表，则漏水点在该水表下的某个水管中；若找到最下级的漏水水表下存在更低级的水表，则漏水点在两级水表的水管之间.

4 供水管网最优维修决策方案

供水管网维修方案需要综合考虑3 个方面：一是管道维修需要的人工费和材料费；二是维修降低管网漏损程度所降低的损失；三是管道更新的投入费用.根据以上3 点构建管道维护更新决策模型.

4.1 管道维修费用模型

管道维修费与漏水口数量、漏水类型等因素相关，费用构成包括人工费、材料费、破路费、机械费等方面［4-6］，管道总的维修费用可以表示成如下公式：

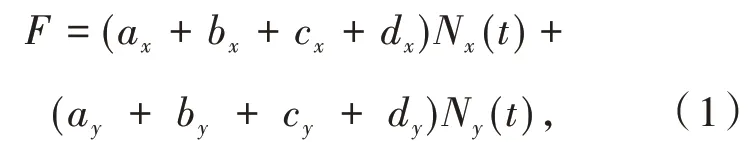
其中：N x(t)表示t年管道口漏数量（处）；N y(t)表示t年折管的漏水口数量（处）；ax表示管道口漏维修的工费（元/处）；ay表示管道折管维修的工费（元/处）；bx表示管道口漏维修材料费（元/处）；by表示管道折管维修材料费（元/处）；cx表示管道口漏维修的破路费（元/处）；cy表示管道折管维修的破路费（元/处）；dx表示管道口漏的机械费（元/处）；dy表示管道折管的机械费（元/处）.

在上述公式中，需要注意的是，不同口径管道的各类维修费用存在较大差距，在分析学校的管道维修费用中应该区别对待.

4.2 水费损失模型

建立漏水水量水费损失模型，损失模型如公式（2）所示：

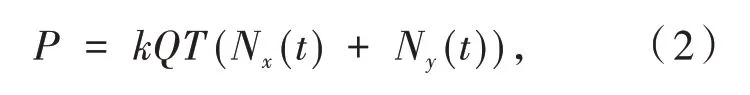
其中：k表示每立方米水的价格；Q表示每处漏水点每天的漏水量；T表示管道漏水持续时间.

管道使用年限越长，因为水管老化等原因发生漏水点的概率越大，因此N x(t) 和N y(t)会随着t增大而增大，维修费用也因此会随着水管老化而增加.

4.3 管道更新费用模型

当水管每年维修费用太高时，需要对管道进行更新，管道更新费用包括设计费、监理费、管道安装费等，管道更新费用可以表示为如下公式：

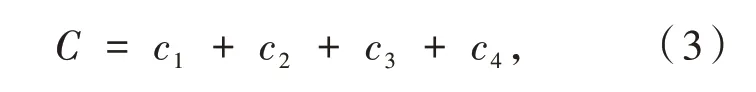
其中：c1=γL，表示管道的材料费用，L表示管道长度，γ表示单位长度的管道费用，γ与管道的粗细、材料等因素相关；c2表示管道附属设施安装费用；c3表示刨路费；c4表示设计费.

4.4 管道维护更新经济决策模型

以经济决策为目标，建立管道更新经济决策模型.

①当P

②当F

③当P>C时，漏水造成的水费损失大于管道更新费用，此时对管道进行更新.

5 模型的应用

将管道维护更新决策模型应用到陇南师专校园供水管网系统管理中，以本校区为实例进行分析.用水区域根据水表布局和功能可划分为教学区、办公区、宿舍区、教师住宅区.根据后勤物业提供的数据，2019 年度本校区用水总量达到了11.139 万立方米.用水量统计及维修情况如表3 所示.

从表3 可以看出，本校区第一季度用水量少，第二季度用水量较多，第三、第四季度差距小.宿舍区和住宅区的漏损相对比较严重，这和用水点多以及管网老化有关，全年用水漏损达到了5.04%.根据全年漏损情况、维修费用、更新费用作出决策，漏损费用（P）为0.561 万 立 方 米×2.5 元/立 方 米=1.402 5 万 元，维修费用（F）达到了1.386 万元，F

然而在实际供水管网维护当中，各季度、各区域的情况都不尽相同.即使水费损失小于维修费用的情况下，为了节省宝贵的水资源，仍然需要进行管网维修，必要时需要进行管网更新.

6 结语

本文基于某校区水表层级关系以及所有水表四个季度的数据变化关系，通过数据挖掘，对每个水表的读数规律进行了统计，并基于此进行功能区域的划分和用水特征分析；对不同级别水表的数据关系进行建模，并完成了模型误差的分析；计算每块水表的漏水比例，进一步完成了整个供水管网的漏损分析，最后提出了供水管道最优维修决策方案，并将模型应用到陇南师专的校园供水管网管理当中，可实现资源浪费最低，经济效益最高的双重目标.

表3 本校区分季度用水量统计及维修费用情况