具有双Allee效应的时滞扩散捕食-食饵模型的时空动力学

2021-03-01练清清裴鑫萍陈云珊蒙伟明汤小松

井冈山大学学报(自然科学版) 2021年6期

练清清，裴鑫萍，陈云珊，蒙伟明，梁盛，汤小松

练清清1，裴鑫萍1，陈云珊1，蒙伟明2，梁盛2，*汤小松1

（1.井冈山大学数理学院，江西，吉安 343009；2.井冈山大学电子与信息工程学院，江西，吉安 343009）

研究了一类具有双Allee效应的时滞扩散捕食-食饵模型。以Allee阈值和时滞为分支参数，利用特征方程和分析技巧讨论了该模型正平衡点的稳定性、扩散诱发的Turing不稳定和时滞诱发的Hopf分支问题。最后，通过数值模拟，获得了该模型的空间周期解和时空斑图，并验证了所得结果的正确性。

捕食-食饵模型；双Allee效应；周期解；时空斑图

捕食者和食饵之间的相互关系及其演化是生态学和生物数学中的重要研究课题，这引起了生物和数学领域中许多学者的极大兴趣。为了刻画捕食者和食饵之间的交互作用及其演化，Lotka[1]和Volterra[2]率先利用微分方程来建立种群间相互作用的数学模型。此后，许多捕食-食饵系统被提出来并获得了大量有意义的研究成果。1931年，美国动物学家Allee提出了Allee效应，即群居有益于种群的生长和存活，但是种群过于稀疏或拥挤都会阻碍其生长，并对繁殖产生副作用，每个物种都有最适宜生长的密度[3]。由于Allee效应对种群动力学有潜在的影响，近年来得到了众多学者的青睐[4-10]。然而，需要指出的是以往的文献只考虑了食饵的Allee效应，而捕食者的Allee效应没有得到考虑。此外，对各种生物种群这样一个群体仅考虑时间是不够的，由于大多数生物种群分别活动在某个空间范围，理应考虑空间的影响。基于以上分析，我们在经典的Lotka-Volterra模型基础之上引入Allee效应和二次死亡率，提出如下时滞扩散捕食-食饵模型：

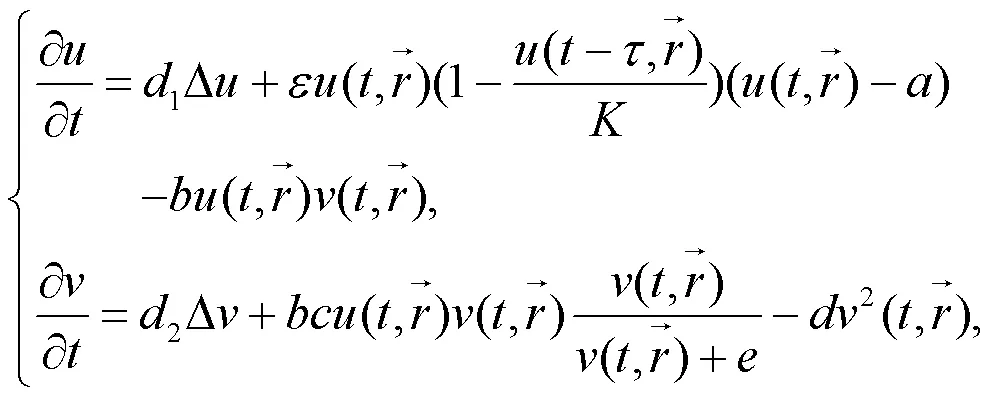
其满足如下Neumann边界条件和初始条件：

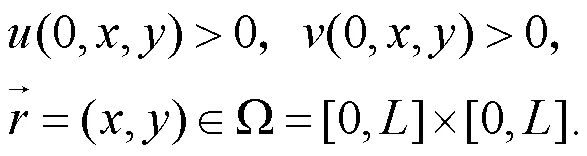
本研究将利用特征方程和分析技巧讨论了模型(1)-(3)正平衡点的稳定性、扩散诱发的Turing不稳定[11-12]和时滞诱发的Hopf分支问题，从而获得该模型的时空动力学行为。

本模型的结构如下：在第1节中，讨论了模型(1)平衡点的存在性，并研究其稳定性以及扩散诱发的Turing不稳定和时滞诱发的Hopf分支问题。在第2节中，通过数值模拟，获得了该系统的空间周期解和时空斑图并验证了所得结果的正确性。最后，我们对本研究作了简要讨论。

1 平衡点和稳定性分析

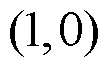
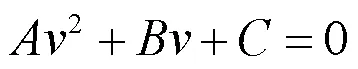
我们仅对情形4的正平衡点进行稳定性分析，其它三种情形也可类似讨论。

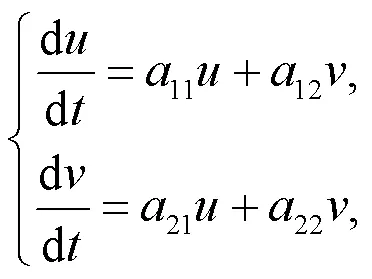
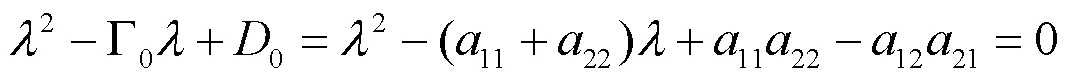
设线性化方程(5)的解形式为

。

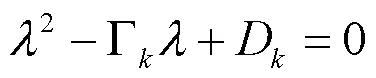
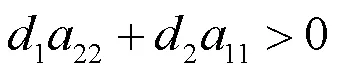
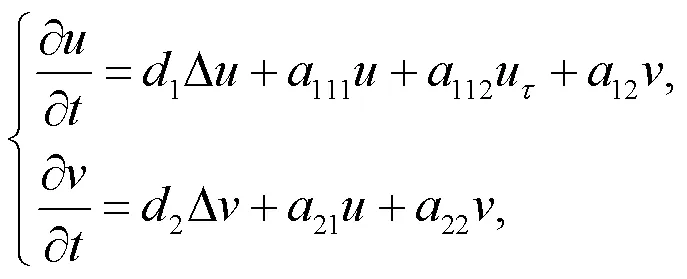
并设线性化方程(6)的解形式为

则对应于线性化方程(6)的特征方程为

其中，

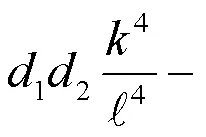
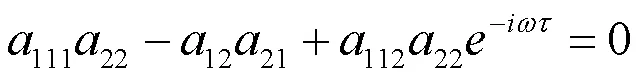
对(8)式分离实部与虚部，则(8)式可化为

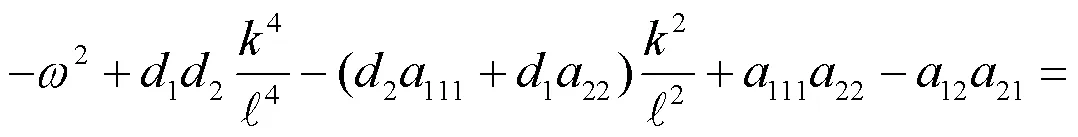
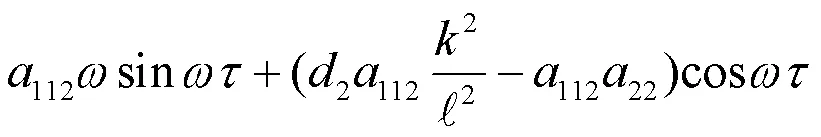
继而，由(9)和(10)可得

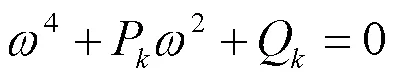
其中

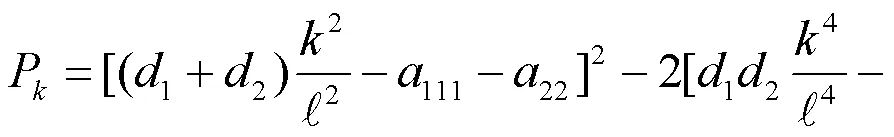
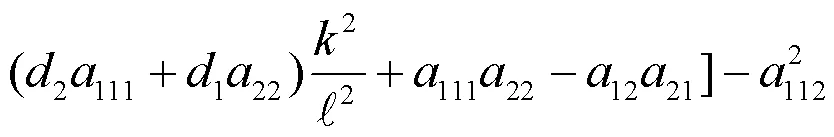
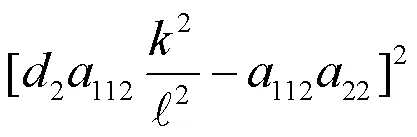
根据一元二次方程解的判定，容易得如下结果：

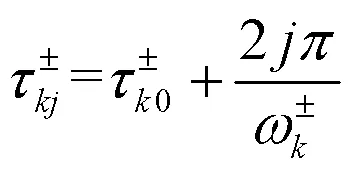
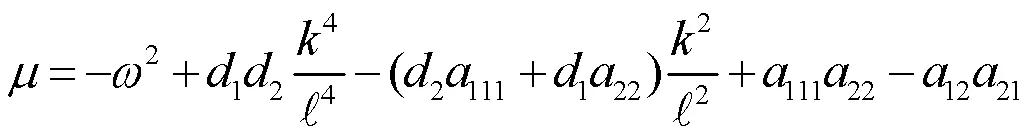
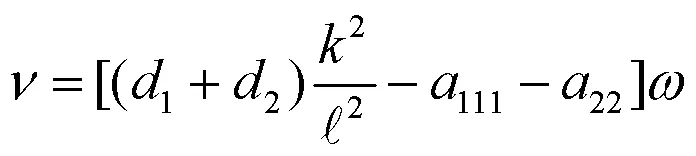
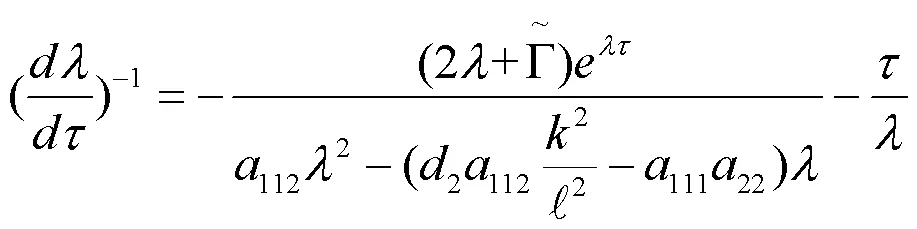
继而，

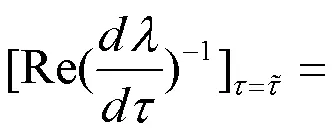
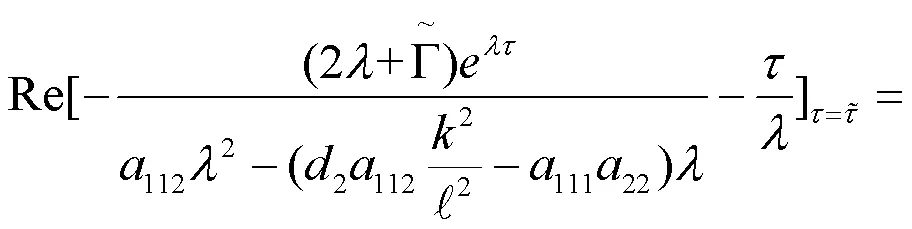
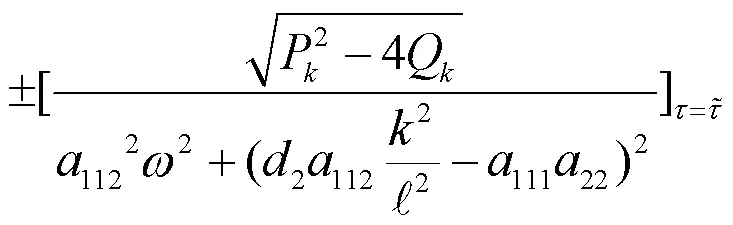
2 数值计算与模拟

在本小节，我们将利用MATLAB软件对模型(1)进行数值计算与模拟，以验证本次结果的正确性。

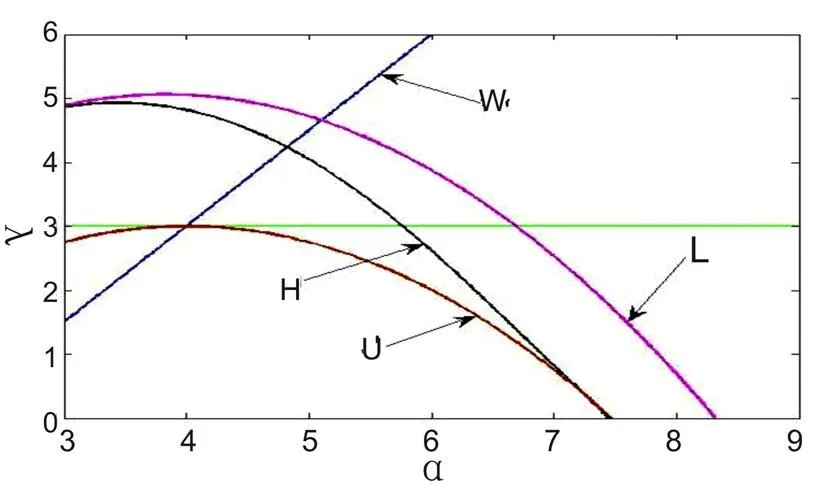
图1 模型(1)的分支图

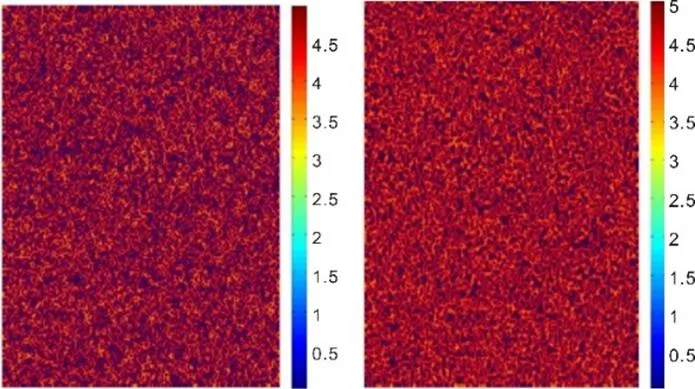
左图：，中图：，右图：

图3 食饵在时的时空斑图

Fig. 3 Snapshots of contour pictures of the time evolution of prey at the moment of t=25000,

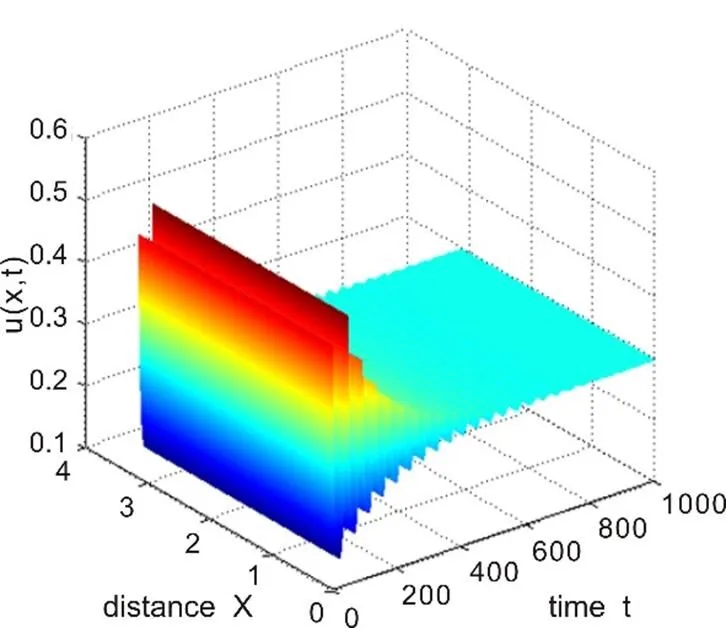
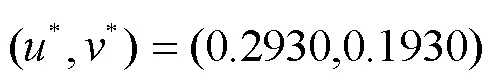
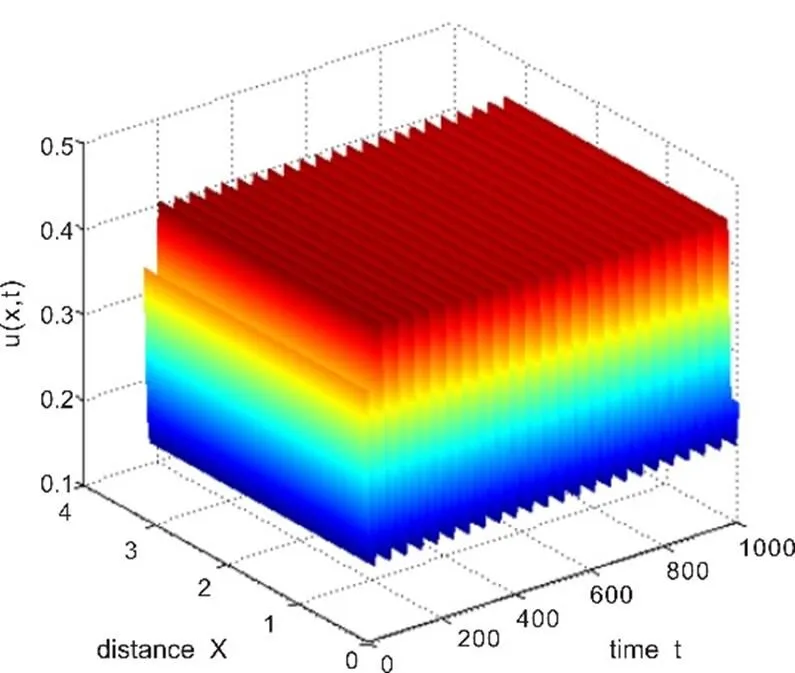
图5 时，稳定的空间周期解

Fig. 5 The stable spatial periodic solutions

图6 时，的局部渐近稳定性

Fig. 6 The locally asymptotical stability of positive equilibrium

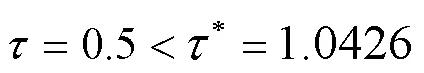
最后，我们对二维空间变量情形进行数值模拟。情形(1)选取初始条件为

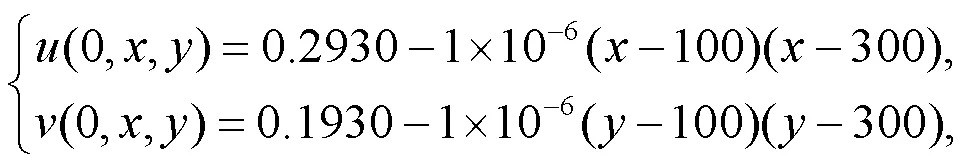
图8 演化时间为500的时空斑图

Fig. 8 Snapshots of contour pictures of the time evolution of prey at the moment of t=500 .

图9 选取时的时空斑图

3 结语

[1] Lotka A J. Sui tentutive di applicazione delle mathematiche alle seienze biologiche e sociali[J]. Ann. Radioelectr. Univ. Romandes,1901,2:3-28.

[2] Volterra V. Variazione e fluttuazini del numero d’individui in specie animali conviventi[J]. Mem. R. Accad. Naz. Dei Lincei, 1926, 2: 31-113.

[3] Allee W C. Animal aggregations: a study in general sociology[M]. Chicago:University of Chicago Press, 1931.

[4] Cui R H, Shi J P, Wu B Y. Strong Allee effect in a diffusive predator-prey system with a protection zone[J]. Journal of Differential Equations, 2014, 256(1):108-129.

[5] Wang X C, Wei J J. Dynamics in a diffusive predator-prey system with strong Allee effect and Ivlev-type functional response[J]. Journal of Mathematical Analysis and Applications, 2015, 422 (2): 1447-1462.

[6] Zhang L M, Zou L. Bifurcations and control in a discrete predator-prey model with strong Allee effect[J]. International Journal of Bifurcation and Chaos, 2018, 28(5): 1850062.

[7] Michel Iskin da S C, Lucas dos A. Multiple hydra effect in a predator–prey model with Allee effect and mutual interference in the predator[J]. Ecological Modelling, 2018, 373: 22-24.

[8] Tyutyunov Y V, Sen D, Titova L I, et al. Predator overcomes the Allee effect due to indirect prey-taxis[J]. Ecological Modelling, 2019, 39: 100772.

[9] Zhang C H, Yuan H L. Pattern formation in a variable diffusion predator-prey model with additive Allee effect[J]. Mathematical Methods in the Applied Sciences, 2020, 43(7): 4023-4035.

[10] Liu Y Y, Wei J J. Spatiotemporal dynamics of a modified Leslie-Gower model with weak Allee effect[J]. International Journal of Bifurcation and Chaos, 2020, 30(12): 2050169.

[11] Turing A L. The chemical basis of morphogenesis[J]. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci., 1952, 237: 37-72.

[12] 欧阳颀. 非线性科学与斑图动力学导论[M].北京:北京大学出版社,2010.

SPATIOTEMPORAL DYNAMICS OF A DELAYED DIFFUSIVE PREDATOR-PREY MODEL WITH DOUBLE ALLEE EFFECT

LIAN Qing-qing1, PEI Xin-ping1, CHEN Yun-shan1, MENG Wei-ming2, LIANG Sheng2,*TANG Xiao-song1

（1. School of Mathematics and Physics, Jinggangshan University, Ji’an, Jiangxi 343009, China; 2. School of Electronics and Information Engineering, Jinggangshan University, Ji’an, Jiangxi 343009, China）

A delayed diffusive predator-prey model with double Allee effect was investigated in this paper. Allee threshold value and delay was chosen as bifurcation parameter, the stability of the positive equilibrium, Turing instability deduced by diffusion and the existence of Hopf bifurcation deduced by delay for this model were discussed by using the characteristic equation and mathematical analysis skills. At last, by performing numerical simulations, the spatial homogeneous periodic solution of this model was obtained, and the validity of theoretical results was illustrated.

predator-prey model; double Allee effect; periodic solutions; spatial patterns

1674-8085（2021）06-0001-07

O175.26

10.3669/j.issn.1674-8085.2021.06.001

2021-07-17；

2021-09-25

国家自然科学基金项目(11761038)；江西省教育厅科技计划项目(GJJ180583)；江西省大学生创新创业训练计划项目(S202010419044)；2019年井冈山大学校级大学生创新创业训练计划项目(2019-74)

练清清(1998-)，女，河南商丘人，井冈山大学数理学院数学与应用数学专业2018级本科生(E-mail:2993959309@qq. com)；

裴鑫萍(1999-)，女，江西丰城人，井冈山大学数理学院数学与应用数学专业2018级本科生(E-mail:1983476687@qq.com)；

陈云珊(2000-)，女，江西赣州人，井冈山大学数理学院数学与应用数学专业2018级本科生(E-mail:2196429188@qq.com)；

蒙伟明(2000-)，男，江西于都人，井冈山大学电子信息工程学院计算机科学与技术专业2018级本科生(E-mail:2715625534@qq.com)；

梁盛(2000-)，男，江西兴国人，井冈山大学电子信息工程学院计算机科学与技术专业2018级本科生(E-mail:2838532805@qq.com)；