基于模糊粗糙集的区间集决策表不确定性度量

唐鹏飞

（四川师范大学 数学科学学院，成都 610066）

0 引 言

粗糙集理论是不确定性分析与智能计算的有效数学工具［1］。目前已广泛应用于属性约简、三支决策和粒度计算等领域［2－4］。

模糊粗糙集将粗糙集和模糊集理论相融合，结合了两者在处理不确定问题方面的优点［5］。目前基于该模型已有诸多研究，例如：文献［6］基于模糊粗糙集提出一种快速约简算法；文献［7］基于距离尺度提出模糊粗糙集模型，定义新的依赖度函数，进而构建其约简算法；文献［8］提出广义正交模糊粗糙集模型，并构建了该模型的属性约简；文献［9］引入决策熵到模糊邻域粗糙集中，刻画其不确定性。可见模糊粗糙集是一种强健的模型结构，值得进一步推广使用。

区间集决策表拓展了经典决策表，其属性值为两个精确集（即用上下边界集来表示一个不确定概念），从而具有更好的不确定性刻画能力，当前具有深入研究［10］。例如：文献［11］基于优势关系，提出4 个基于粒度的区间集信息表的不确定性度量；文献［12］将区间集引入到概率粗糙近似中，研究区间集概率粗糙集的单调性；文献［13］基于δ－相似关系，研究区间集信息表的不确定性度量；文献［14］提出决策条件熵刻画区间集决策表的不确定性；文献［15］提出修正δ－区间决策条件熵刻画区间集决策表的不确定性。

综上所述，基于模糊粗糙集的区间集决策表不确定性度量研究暂未发现。因此，本文将模糊粗糙集引入到区间集决策表，研究其不确定性度量。首先，基于模糊粗糙集，提出模糊近似粗糙度和模糊近似精度；其次，在信息论视角下，提出模糊粒结构和模糊条件熵；最后，将两者进行信息集成，提出一种基于模糊粗糙集的混合不确定性度量，并研究了相关性质。

1 预备知识

1.1 模糊粗糙集理论

模糊决策表记为FDS＝｛U，AT＝C∪D，V，f｝，其中论域U＝｛x1，x2，…，xn｝ 是一个非空有限对象集，C，D分别表示条件属性集与决策属性集，V＝∪a∈ATVa是属性值集，f：U × AT→V是（x，a）→μa（x）的信息函数，这里μa（x）∈［0，1］ 表示对象x在属性a下的属性值。

定义1［5］在FDS中，模糊相似关系可由式（1）的相似度导出：

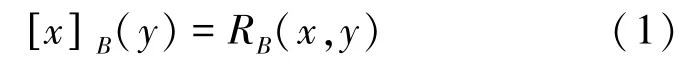
其中，RB（x，y）∈［0，1］ 表示对象x和y在属性集B下的相似度。模糊相似关系可导出相应的模糊相似类，式（2）：

以及模糊相似分类，式（3）：

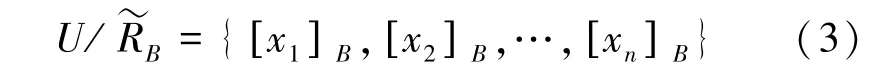
决策划分U／D＝｛D1，…，Dm｝，其中Dh（1 ≤h≤m）表示决策类。实际上Dh可以看成是一个特殊的模糊集，即式（4）：

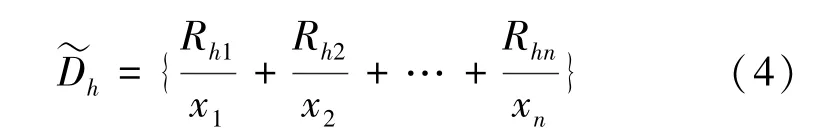
其中，如果xj∈Dh，则Rhj＝1；如果xj∉Dh，则Rhj＝0，1 ≤j≤n。

定义2［5］在FDS中，对象x在条件属性集B下，关于模糊集的模糊下、上近似分别为式（5）：

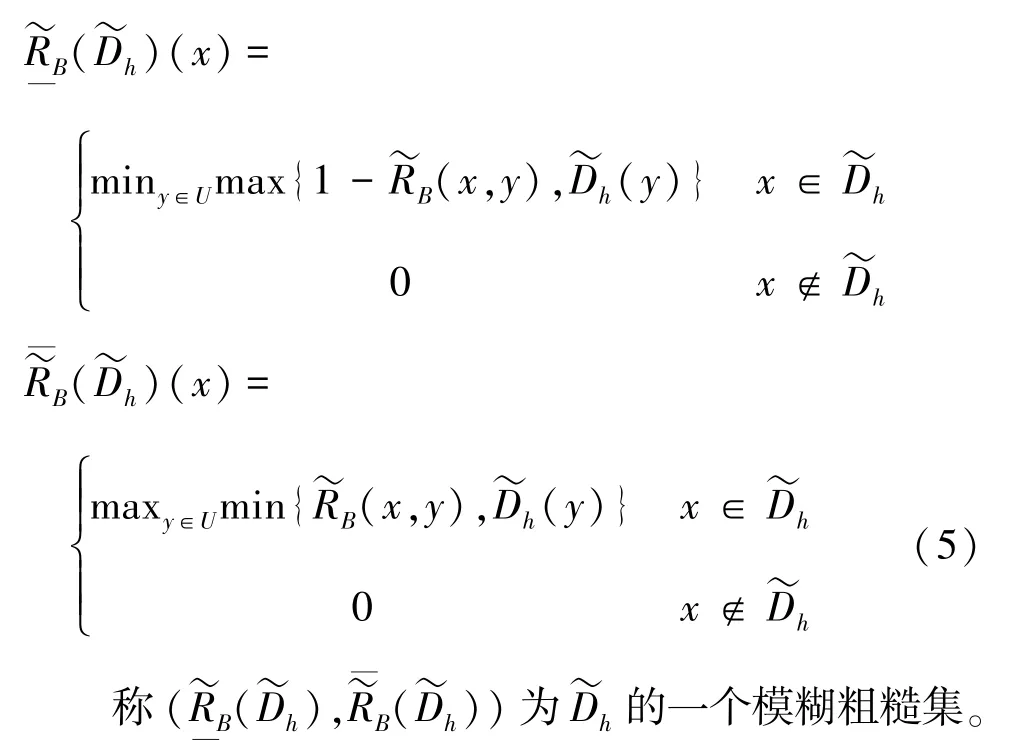
1.2 区间集决策表

定义3描述了对象之间的关系，因对象在条件属性下的取值为区间集，带有模糊性，考虑到模糊粗糙集模型处理模糊数据的优越性，下面将其引入到区间集决策表研究不确定性度量。为此，首先建立模糊粗糙集模型。

2 基于模糊相似关系的模糊粗糙集模型

基于定义1、3，相似关系也可视为论域U上的二元模糊相似关系。基于模糊相似关系，定义条件属性子集的模糊相似类及关系矩阵，推广模糊上下近似算子，并研究其相关性质。下面先给出模糊相似类的定义。

定义4设区间集决策表IDS＝｛U，AT＝C∪D，V，f｝，条件属性子集B⊆C，B诱导的模糊相似关系记为为U上的决策模糊集，则模糊集关于属性B的模糊下、上近似分别为式（7）：

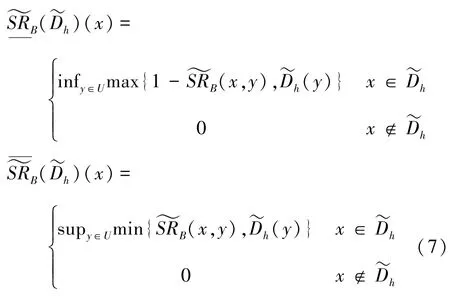
3 区间集决策表的不确定性度量

经典决策表的不确定性度量是基于等价关系提出的，不适用于区间集决策表。本节基于模糊粗糙集模型，定义区间集决策表不确定性度量的相关概念和性质，并在理论上加以证明。

3.1 模糊近似粗糙度和模糊近似精度度量

基于模糊粗糙集模型，给出区间集决策表中的不确定性度量概念：模糊近似精度和模糊近似粗糙度。其通过粗糙集边界域的视角去刻画区间集决策表的不确定性。

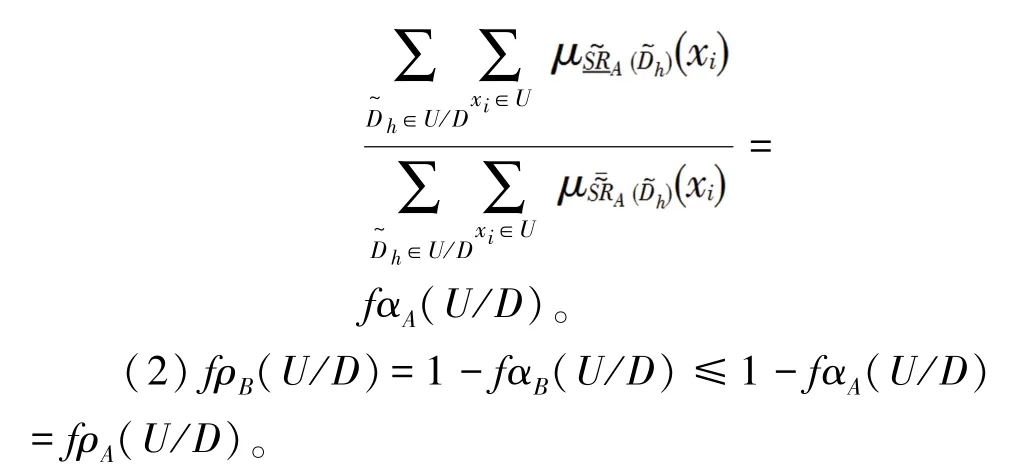
定理3 表明，模糊近似精度、模糊近似粗糙度具有关于属性的粒化单调性，能够度量上、下近似产生的不确定性。

3.2 基于模糊条件熵的混合不确定性度量

模糊近似粗糙度从边界域角度刻画了区间集决策表的不确定性，忽略了知识划分对区间集决策表不确定性的影响，下面引入模糊条件熵，提出一种基于模糊条件熵的混合不确定性度量来多角度地度量区间集决策表的不确定性。在此之前，先基于模糊相似关系，定义模糊粒结构。

定理4设区间集决策表IDS＝｛U，AT＝C∪D，V，f｝，属性子集A，B⊆C，由A，B决定的模糊粒结构分别为G（A），G（B）。则下列结论成立。

（1）FH（D ｜A）≥0，FH（D ｜B）≥0

（2）如果G（B）＝G（A），则FH（D｜B）＝FH（D｜A）

（3）如果A⊆B，则FH（D ｜A）≥FH（D ｜B）

证明（1）由定义可知显然成立。

定理4 表明，模糊条件熵满足不确定性公理化定义的非负性、不变性、单调性，是一种有效的度量方式，但其只能刻画粒化结构的不确定性。

在定义8 中，模糊近似粗糙度从代数角度描述近似分类的不确定性，本质上是衡量区间集决策表中所包含有效知识的量，而定义10 中模糊条件熵从信息角度度量粒化结构的不确定性，本质上是通过粒化结构的每个粒子平均所含信息量的大小对不确定性进行刻画。由于模糊近似粗糙度和模糊条件熵两者都满足单调性，且两者是从不同视角度量区间集决策表的不确定性，各自具有优越性。因此，为了对区间集决策表的不确定性达到一种更为全面的评估，下面提出一种基于模糊条件熵的混合不确定性度量来刻画区间集决策表的不确定性。

定义11设区间集决策表IDS＝｛U，AT＝C∪D，V，f｝，属性子集B⊆C，决策划分U／D关于B的模糊近似粗糙度与模糊条件熵分别为fρB（U／D），FH（D ｜B）。那么基于模糊条件熵的混合不确定性度量为式（20）：

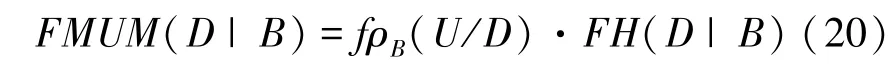
定理5设区间集决策表IDS＝｛U，AT＝C∪D，V，f｝，属性子集A⊆B⊆C，那么混合不确定性度量满足式（21）：

基于定义11 的乘积融合定义，定理5 所述的粒化单调性自然成立。混合不确定性度量融合了模糊近似粗糙度和模糊条件信息熵的优点，既能度量上、下近似产生的不确定性，又能表征粒化结构变化时不确定性的变化，该度量与单一度量方式相比更加全面，可以弥补两种度量之间的不足。

4 举例分析

为了更好的说明本文提出的不确定性度量方法的有效性，下面通过一个实例来说明计算方法和结果。

举例：区间集决策表IDS见表1［14］，其中U＝｛x1，x2，x3，x4，x5，x6｝，C＝｛a1，a2，a3｝，D＝｛d｝。

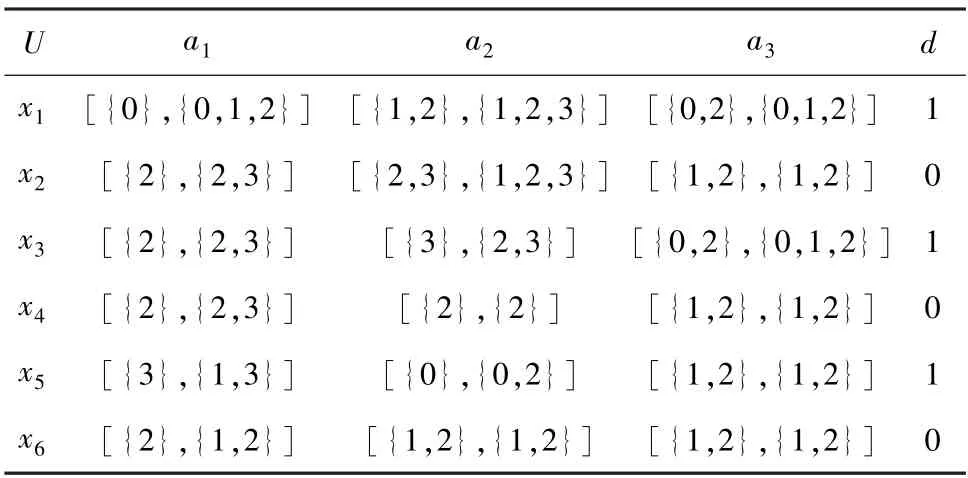
表1 区间集决策表Tab.1 Interval set decision table

通过计算得到属性a1，a2，a3的模糊相似矩阵分别为。

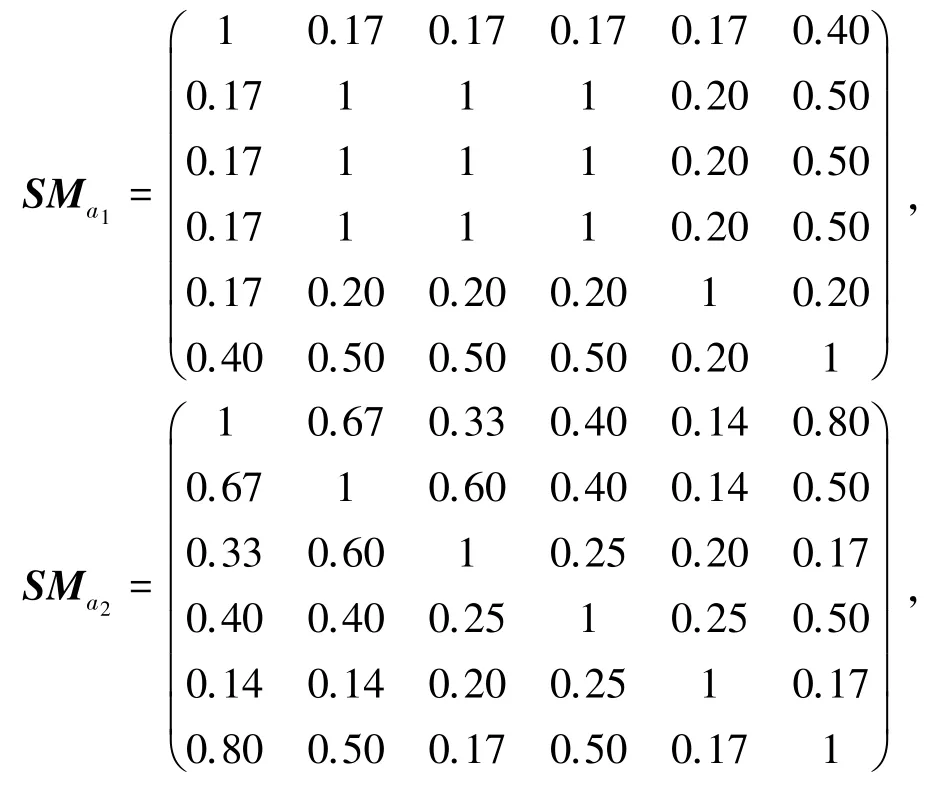
假设A＝｛a1，a2｝，B＝｛a1，a2，a3｝，则属性集A，B的模糊相似矩阵分别为SMA，SMB。

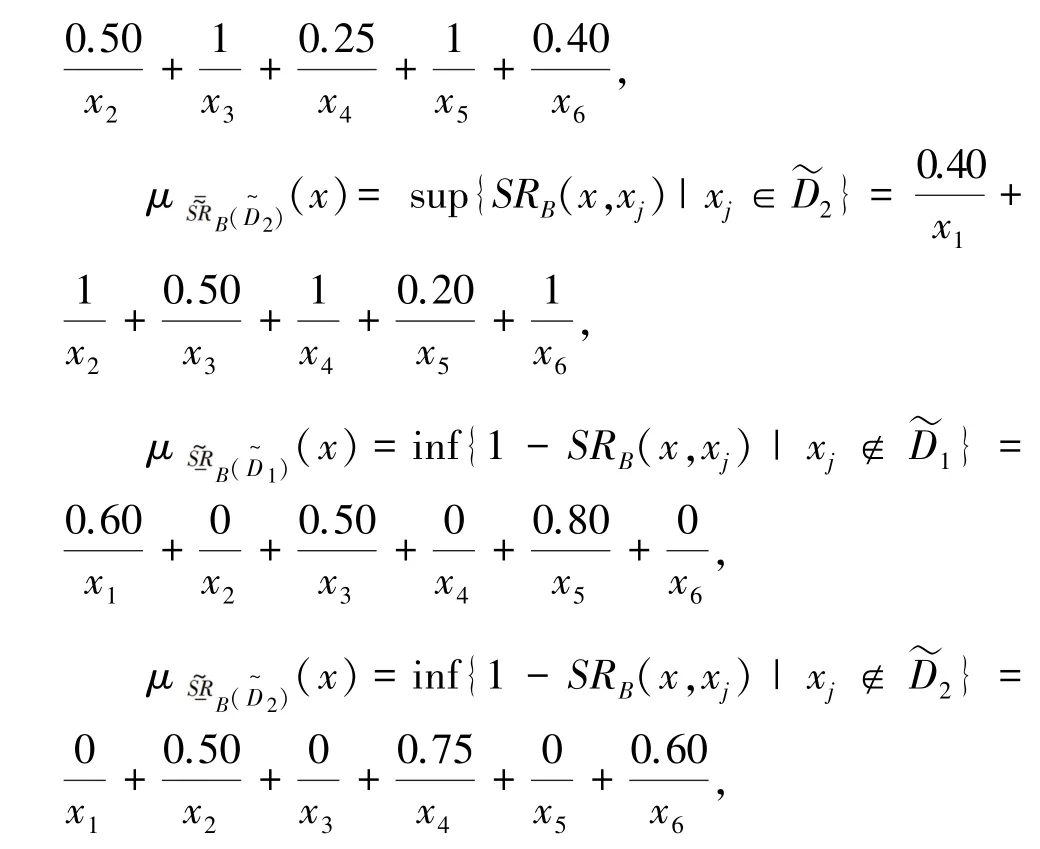
通过定义8 可得决策划分U／D关于A，B的模糊近似精度和模糊近似粗糙度分别为：

fαA（U／D）＝0.42，fρA（U／D）＝0.58，

fαB（U／D）＝0.52，fρB（U／D）＝0.48，

fαA（U／D）≤fαB（U／D），fρA（U／D）≥fρB（U／D）。与定理3 一致。

通过定义10 可得决策划分U／D关于A，B的模糊条件熵分别为：

FH（D ｜A）＝1.01，FH（D ｜B）＝0.97.

则FH（D ｜A）≥FH（D ｜B），与定理4 一致。

通过定义11 可得决策划分U／D关于A，B的混合不确定性度量分别为：

FMUM（D ｜A）＝0.59，FMUM（D ｜B）＝0.46。

则FMUM（D ｜A）≥FMUM（D ｜B），与定理5一致。

5 结束语

本文通过引入模糊粗糙集模型，定义模糊近似粗糙度和模糊条件熵，并将两者进行信息融合，提出一种基于模糊条件熵的混合不确定性度量，其从两个不同的角度刻画区间集决策表的不确定性，是一种更加全面、有效的度量方法。实例表明，所提度量对研究区间集决策表的不确定性具有指导作用。在未来工作中，可将本文所提度量用于构建区间集决策表的属性约简。