列车紧急制动过程中踏面温度分布及磨耗预测

2021-02-28董永刚黄鑫磊宋剑锋杜晓钟

中国机械工程 2021年4期

董永刚仪帅黄鑫磊宋剑锋杜晓钟

1. 燕山大学机械工程学院，秦皇岛，066004 2. 太原科技大学机械工程学院，太原，030024

0 引言

高速重载列车在制动过程中，车轮踏面与闸瓦间的摩擦将车辆动能转换为热能，摩擦产生的热量使得踏面温度急剧上升，而温度的升高会导致车轮材料的硬度以及屈服强度明显降低，踏面表层局部金属处于塑性状态，在轮轨接触斑接触应力、闸瓦制动压力及热应力综合作用下，车轮踏面表层同时与钢轨和闸瓦发生高温、高速滚动和滑动接触摩擦磨损。这两种不同接触摩擦状态的磨损机理差异较大又同时发生，而且制动过程产生的摩擦温升影响车轮钢材料的物理性能参数、机械性能参数以及轮轨接触区、轮瓦接触区摩擦因数和磨损系数，导致踏面制动过程中的踏面磨损机理非常复杂。肖绯雄等[1]通过对不同制动工况下货车用高摩合成闸瓦进行仿真分析，对相同工况下不同磨耗程度的闸瓦温度场进行曲线拟合，计算了闸瓦在不同工况下的磨耗量，结果表明: 工况越恶劣闸瓦每万公里的磨耗量就越大，相应地，闸瓦所能达到的最高温度也越高。杨新文等[2]利用MATLAB软件编制了轮轨接触热效应分析程序，针对不同的轮对横移量、车轮移动速度、摩擦因数和相对滑动速度进行了钢轨的温度场研究，结果表明: 轮轨滑动接触热效应剧烈，会导致轮轨接触表面发生擦伤、裂纹和剥离等热损伤。陈帅等[3]考虑踏面制动温升对车轮、钢轨硬度的影响，建立了重载铁路车轮磨耗模型，并预测了车轮踏面磨耗，结果表明: 重载铁路踏面制动摩擦温升会加剧车轮磨耗，考虑摩擦温升时车轮总磨耗体积增大12.1%，当制动温升达到最高时最大磨耗深度增大22.5%。MANDEEP等[4]通过对通勤列车进行现场测试，得到车轮辐板与闸瓦的温度以及车轮踏面和闸瓦的磨损量，结合考虑温度效应的销盘式磨损试验，给出了一个磨损率适应因子，对现有高温磨损率公式进行了修正。KATSUYOSHI 等[5]为了研究由于塑性变形以及由滚动接触和踏面制动引起的磨损，在轮轨滚动接触的基础上进行了一系列的踏面制动实验，结果表明: 当紧急制动循环重复40次时，滚动接触中心的踏面磨损深度最大达到0.2 mm。

众多学者研究表明，温度是车轮踏面磨损不可忽视的影响因素。本文综合考虑踏面制动温升对材料属性、接触状态的影响，利用ABAQUS软件建立踏面制动过程三维瞬态热-机械耦合有限元模型，仿真得到踏面温度随制动时间的动态变化规律，并通过动力学方法得到相同制动工况下轮轨接触斑内滑移量，最后基于Archard理论分别计算了轮轨间磨损和闸瓦与踏面间的磨损深度，并得到了制动结束后的踏面磨损轮廓。

1 踏面制动过程模型的建立

1.1 有限元模型的建立

利用有限元软件ABAQUS建立闸瓦-车轮-轨道模型，如图1所示。车轮直径为0.86 m、材料为CL60车轮钢、标准LM型踏面；闸瓦选择常见的高磷铸铁闸瓦，闸瓦宽度为0.06 m，弧长为车轮圆周长的五分之一；轨道轮直径为1 m，材料为U71Mn，轨道轮型面按照75 kg/m标准断面轨尺寸进行建模。将闸瓦力均匀施加在闸瓦钢背处，同时仅保留其沿车轮径向方向的自由度。轴质量载荷施加在车轮中心约束点P1上，P1与车轮轴孔进行耦合，同时仅保留车轮绕轴旋转自由度。轨道轮保留绕轴孔旋转的自由度，温度边界条件设为恒温26℃。选择动力-温度位移-显示分析步，车轮、闸瓦、轨道轮网格均划分为8节点热耦合六面体单元C3D8T，为了得到较好的仿真效果，对车轮踏面接触区域网格进行细化处理，如图2所示。

图1 闸瓦-车轮-轨道三维模型Fig.1 Three-dimensional model of brake shoe-wheel-track

图2 闸瓦-车轮-轨道有限元模型Fig.2 Brake shoe-wheel-track finite element model

1.2 接触属性设置

列车动能主要通过闸瓦与车轮摩擦方式转化为热能，但由于制动时速度变化较快，轮轨间相对滑移量相对增大，因此蠕滑产生的热量也是整个热能系统重要组成部分。摩擦产生的热量一部分传递到闸瓦与轨道轮上，但大部分会通过踏面传递到车轮，车轮吸收的热量占总摩擦热能的百分比称为热量分配系数，在有限元仿真时热量分配系数设置为0.90[6]，闸瓦与车轮踏面间摩擦因数f1根据经验公式[7]有

(1)

αm=0.3828+14.39vt

(2)

vt=v0-kt

(3)

式中，FN为闸瓦压力，kN；vt为行驶速度， km/h；v0为初始速度， km/h；t为制动时间；k为减速度；αm为传热系数。

整个制动系统热辐射系数根据经验值取0.66[8]，am依据式(2)取值[9]。以FN为30 kN，轴质量为20 t，v0为130 km/h和160 km/h为例，通过式(1)、式(2)得到闸瓦摩擦因数与对流传热系数随制动时间t的变化曲线如图3所示。轮轨间接触类型选择面-面接触，考虑到温度对摩擦副摩擦因数会有一定的影响，文献[10]中通过实验测得了不同温度下轮轨间摩擦因数f2，如图4所示。

1.αm(vt=130 km/h) 2.αm(vt=160 km/h)3.f1(vt=130 km/h) 4.f1(vt=160 km/h)图3 摩擦因数f1、传热系数随制动时间变化Fig.3 Friction coefficient f1、 convective heat transfer coefficient changes with braking time

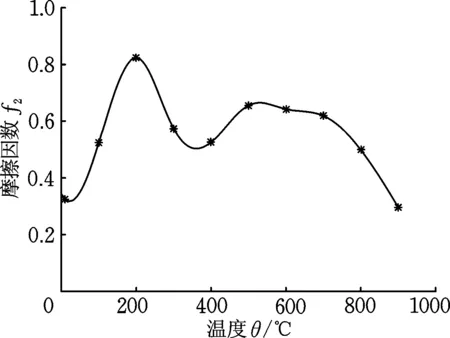
图4 不同温度下轮轨间摩擦因数Fig.4 Friction coefficient between wheel and rail at different temperatures

1.3 材料属性设置

列车在紧急制动过程中，车轮和闸瓦的温度在短时间内急剧升高，高温导致材料的机械性能(如弹性模量、抗拉强度、屈服强度等)与热物理特性(如质量热容、热膨胀系数、热导率等)发生改变，从而影响车轮的温度场和应力场。目前很难得到从常温到600 ℃区间内车轮钢CL60、高磷铸铁闸瓦的机械性能及物理性能参数的动态变化，因此本文通过JMatPro软件得到了不同温度下材料的力学性能及热物性参数。

车轮钢材料的密度为7850 kg/m3，泊松比μ为0.3，表1列举了部分不同温度下车轮钢材料参数。闸瓦材料密度为6740 kg/m3，泊松比μ为0.28，表2列举了部分不同温度下闸瓦材料参数。由于在仿真中轨道始终保持恒温，因此不需设定高温下的材料参数，轨道材料的密度为7830 kg/m3、泊松比μ为0.29、抗拉强度为883 MPa、质量热容为430 J/(kg·℃)、热膨胀系数为1.197×10-5/℃、热导率为47 W/(m·℃)、弹性模量E为210 GPa、屈服强度为620 MPa。车轮材料引入双线性等向强化准则，线性强化塑性材料模型如图5所示(其中，θ为材料的温度)，强化模量如下：

(4)

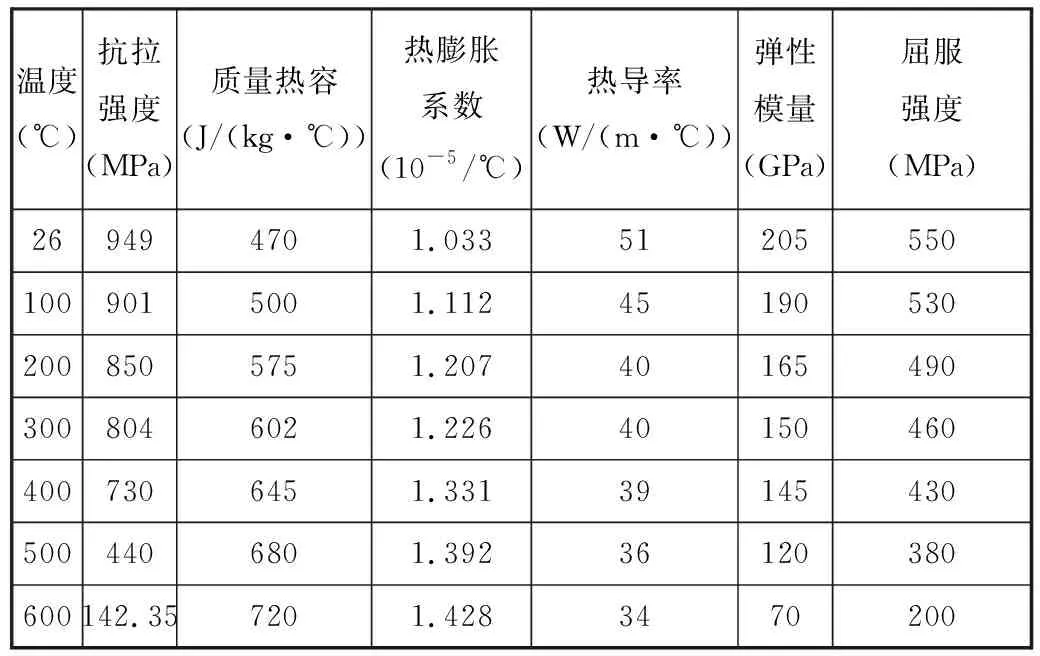
表1 CL60车轮钢材料参数Tab.1 CL60 wheel steel material parameters

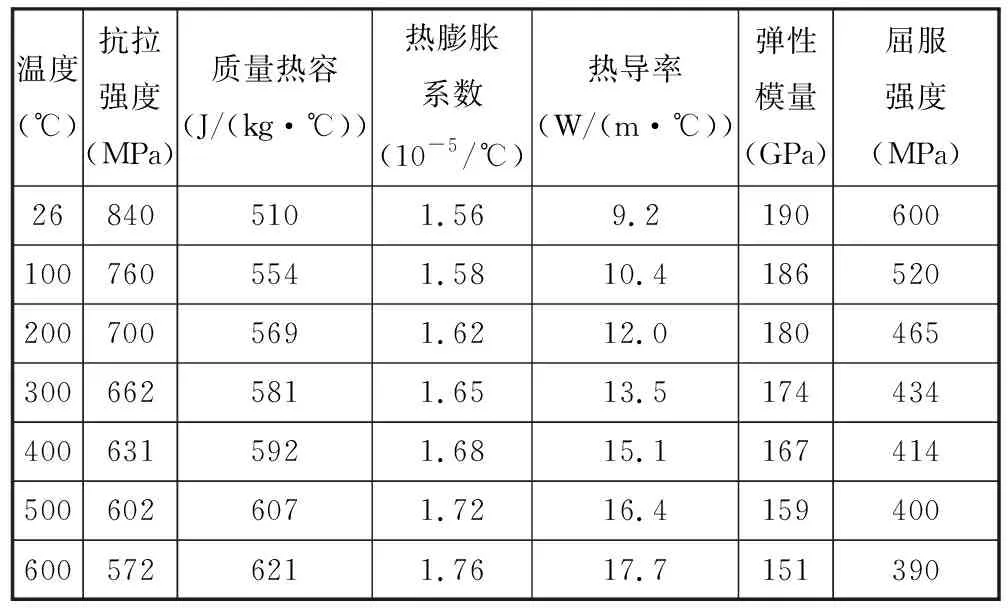
表2 闸瓦材料参数Tab.2 Brake shoe material parameters

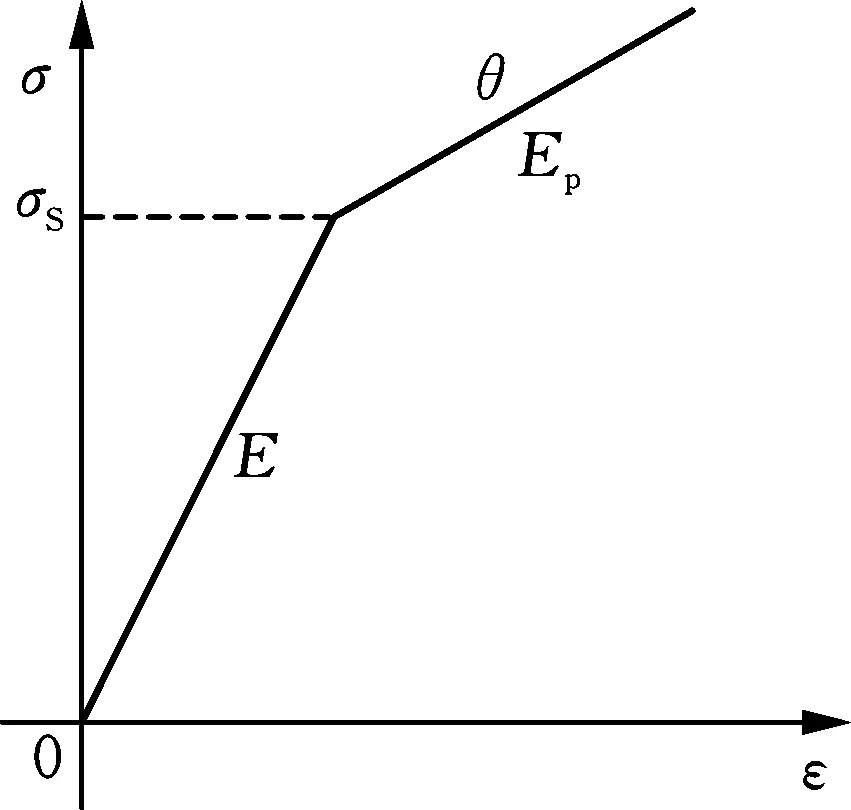
图5 某温度下弹塑性曲线Fig.5 Elastic-plastic curve at a certain temperature

1.4 动力学模型的建立

借助多体动力学软件UM(universal mechanism)建立货车-轨道动力学仿真模型，车体采用传统三大件式货车转向架，如图6所示。模型中将钢轨视为无质量的黏弹性力元结构，只考虑钢轨与轨道板在横向和垂向的刚度和阻尼，不考虑钢轨的惯性矩。轮轨型面及摩擦因数等参数与1.2节中相同，轨道设定为不平顺轨道，轨道谱类型选用美国5级轨道不平顺谱。对于轮轨接触模型，采用Hertz理论以及Kalker的FASTSIM算法，将1.2节中仿真得到的制动速度-时间关系导入到UM中，进行接触斑形状及蠕滑区轮轨滑移量等的仿真。

图6 货车-轨道动力学模型Fig.6 Freight car-track dynamic model

为保证有限元仿真与动力学仿真结果的一致性，分别对轴质量、制动速度、轨道型面、车轮型面、摩擦因数、车轮与轨道的材料属性等进行相同设置。

2 考虑温度效应的磨耗预测理论

Archard磨损公式在轮轨磨耗研究中得到了广泛应用，表达式如下：

(5)

式中，H为材料硬度，HB；P为法向压力，N；V为材料磨损体积，m3；S为相对滑移距离，m；K为量纲一磨损系数。

踏面制动过程中，车轮每转过一周，车轮型面上磨损包括两部分：闸瓦与踏面的磨损、钢轨与踏面的磨损。为了将Archard磨损公式运用到有限元分析中，需要对其进行修正，通过每个节点的磨损量来表示踏面磨损情况。

2.1 轮轨间磨损计算

列车在制动时，接触斑内滑移量很大，磨损很剧烈。首先建立接触斑局部坐标系，设车轮滚动方向为x正向，轴向方向(车轮外侧至轮缘侧)为y正向。轮轨接触斑磨耗模型如图7所示，将接触斑划分为若干大小相同的单元，每个单元的长度和宽度分别为dx、dy，每个单元面积dA=dxdy。

图7 轮轨接触斑磨耗分布计算模型Fig.7 The calculation model of wheel-rail contact patch wear distribution

接触斑内任一单元的磨损深度为

(6)

式中，K1为轮轴间磨耗系数。

根据Hertz接触理论，得到接触斑内应力分布：

(7)

式中，a、b为接触斑的长短半轴长。

由于车轮转过接触斑时间极短，所以视整个接触斑内踏面温度相同，车轮钢材料的硬度与温度关系[3]有经验式：

H(θ)=-0.3θ+332

(8)

实际制动时的轮轨型面及接触位置如图8a所示，车轮磨耗仅发生在接触斑蠕滑区内，图8b中阴影部分为黏着区，接触斑内部除黏着区之外空白区域为蠕滑区。在制动系统全局坐标系下，轮轨间磨损仅发生在接触斑的宽度范围(e≤y≤f)内，闸瓦磨损的范围为0≤y≤L，其中，e、f为接触斑短轴的y向坐标，L为闸瓦宽度。

(a) 轮轨型面及接触位置

(b) 黏着区

车轮每转过一圈与钢轨接触一次，接触斑单元磨耗深度由式(6)计算得到，沿滚动方向将所有单元的磨损进行叠加，便得到踏面滑过一个接触斑后的磨损深度，由于在制动过程中不同时刻的磨损状态也不一样，所以当车轮制转过第i圈时，接触斑内磨损深度为

(9)

轮轨间磨耗系数K1=4.0×10-4[11]，由于接触斑内不同位置处的滑移量大小不同，在计算时，统一选择最大滑移量dSimax进行计算，其值由UM动力学仿真结果得到。

2.2 闸瓦与踏面磨损计算

车轮每转过一圈，踏面节点经过闸瓦接触区时相对滑移量为定值2πR/5(R为车轮半径)，当车轮转过第i圈时，踏面磨损深度为

(10)

其中，K2为闸瓦与车轮踏面间的磨耗系数，K2=8.0×10-5，通过文献[12]中闸瓦磨损实验数据进行反向推导得到；闸瓦与轮轨间的接触应力p2(y)和踏面硬度H(θ)可在ABAQUS后处理中提取。

假设在一次连续制动结束后，车轮总共转过n圈，在踏面上沿y方向选取一排固定节点集，假定该节点集内含有l个节点，则节点集内任意点处踏面总的磨损深度即为轮轨接触区磨损深度与闸瓦接触区磨损深度之和(其中，1≤i≤n)，其表达式为

(11)

由于在接触斑之外的区域没有磨损，故其磨损深度变为零,即

ΔD1(y,n)=0(0≤y≤e,f≤y≤L)

(12)

依次求出l个节点的磨损深度，即可表征制动结束后车轮踏面的磨损轮廓。

3 仿真结果分析

以表3中的参数进行制动过程仿真，图9为制动过程中踏面温度达到最高时刻仿真图。当初始速度为130 km/h时，制动第26 s时踏面温度达到最高温度397.00 ℃(图9a)；当初始速度为160 km/h时，制动第32 s时踏面温度达到最高温度485.90℃(图9b)。最高温度集中在车轮踏面中部区域，车轮外侧与空气对流换热面积较大，因此热量散失得相对较快，其温度低于踏面中部温度。在车轮内侧靠近轮毂处的踏面与闸瓦没有直接摩擦，因此温度也低于踏面中部温度。

表3 制动工况参数Tab.3 Braking conditions parameters

(a)v0=130 km/h,t=26 s

(b)v0=160 km/h, t=32 s

在踏面上沿轴向方向选择一排固定的节点集，提取温度数据通过MATLAB绘图得到完整制动过程踏面温度分布，如图10、图11所示。在制动初期，由于车轮旋转速度较快，与闸瓦间摩擦较为剧烈，因此温度上升迅速，随着速度的逐渐减小，温度逐渐攀升至峰值，在此时间点之后，摩擦产生的热量小于散射的热量，踏面温度逐渐降低。

图10 制动速度为130 km/h时车轮踏面温度分布Fig.10 Temperature distribution of the wheel tread with braking speed of 130 km/h

图11 制动速度为160 km/h时车轮踏面温度分布Fig.11 Temperature distribution of the wheel tread with braking speed of 160 km/h

将整体温度数据代入式(8)，得到车轮踏面硬度随温度变化图，见图12、图13。温度升高使车轮材料的硬度发生明显的降低，初速度为130 km/h制动时最低硬度为212.6 HBW，初速度为160 km/h制动时最低硬度为186.23 HBW。

图12 制动速度为130 km/h时车轮踏面硬度分布Fig.12 Hardness distribution of wheel tread with braking speed of 130 km/h

图13 制动速度为160 km/h时车轮踏面硬度分布Fig.13 Hardness distribution of wheel tread with braking speed of 160 km/h

由图9可知，制动过程中温度最高处位于踏面中间位置，分别提取工况1、工况2下踏面中间位置的温度值，得到踏面温度、制动速度与制动时间的关系，如图14所示。图15为踏面中部区域材料硬度随制动时间的变化图。

1.温度(vt=130 km/h) 2.温度(vt=160 km/h)3.速度(vt=130 km/h) 4.速度(vt=160 km/h)图14 车轮速度及踏面中部温度随时间变化曲线Fig.14 Wheel speed and temperature in the middle of the tread over time

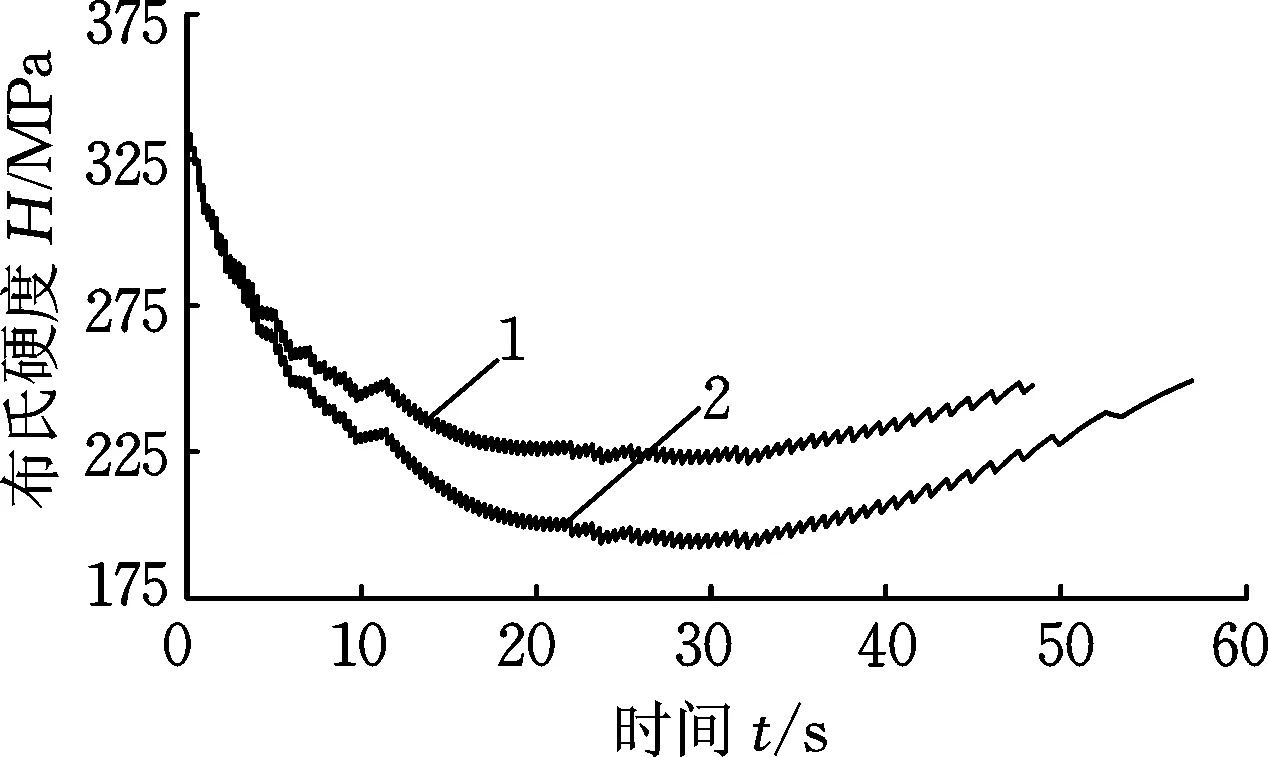
1.vt=130 km/h 2.vt=160 km/h图15 车轮踏面中部硬度随时间变化曲线Fig.15 The hardness of the middle of the wheel tread changes with time

由于制动过程中闸瓦压力和轴质量保持不变，而轮轨接触区接触斑形状和闸瓦接触区形状随温度变化很小，温度变化对应变影响显著而对接触应力的影响很小，因此认为在制动过程中车轮踏面上的接触应力分布只与轴质量和闸瓦压力有关。由于轨道不平顺作用，接触斑的大小变化很小，如图16所示。选取某一时刻的接触斑(a=9，b=4)结合式(7)可以求解出接触斑内的应力分布，如图17所示。闸瓦与踏面接触区的应力可用闸瓦中部截面上的应力代替，如图18所示。

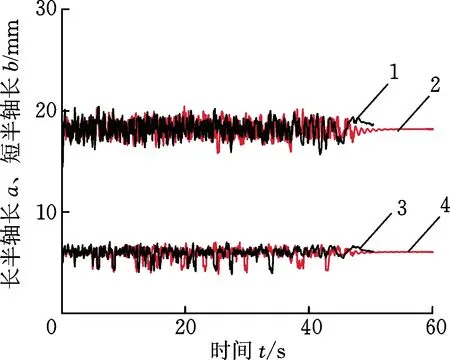
1.长半轴长(vt=130 km/h) 2.长半轴长(vt=160 km/h)3.短半轴长(vt=130 km/h) 4.短半轴长(vt=160 km/h)图16 接触斑内应力分布Fig.16 Stress distribution in the contact spot

图17 接触斑内应力分布Fig.17 Stress distribution in contact spot

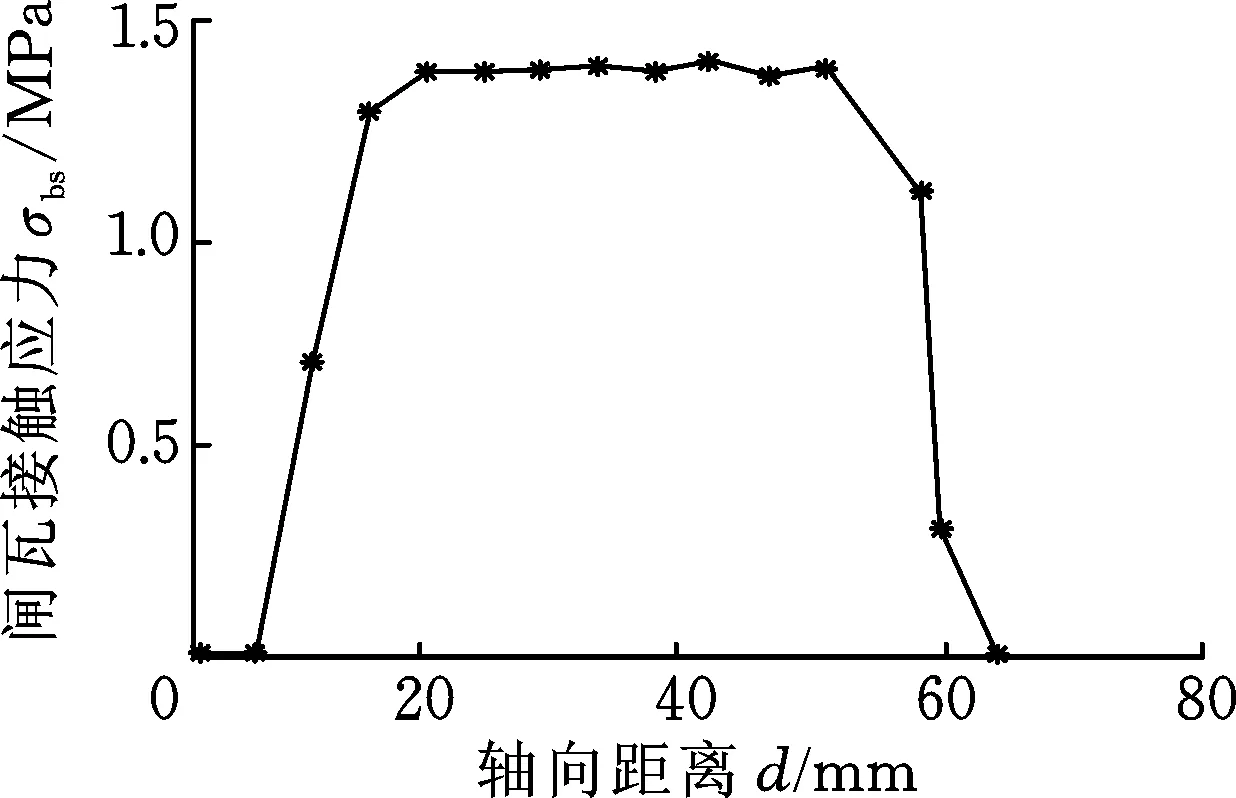
图18 闸瓦截面应力分布Fig.18 Stress distribution of brake shoe section

在UM中提取两种初速度下多个时间节点的接触斑，如图19所示。由于轴质量、轮轨型面等因素保持不变，因此接触斑的形状及大小变动幅度很小，而制动参数、轨道不平顺激励等因素对滑移区的大小产生较为明显的影响，接触斑内最大滑移量变化幅度较为剧烈，如图20、图21所示。从数据分布来看，制动初速度为130 km/h时的平均滑移量为1.38 mm，制动初速度为160 km/h时的平均滑移量为1.02 mm，尤其在制动初期，滑移量大小差别较大，在制动后期，列车速度大幅度减小，此时滑移量的变化幅度逐渐趋于稳定。根据图3中摩擦因数与速度的曲线，相同制动力下速度越大其摩擦因数越小，则切向蠕滑力与滑移量也越小。

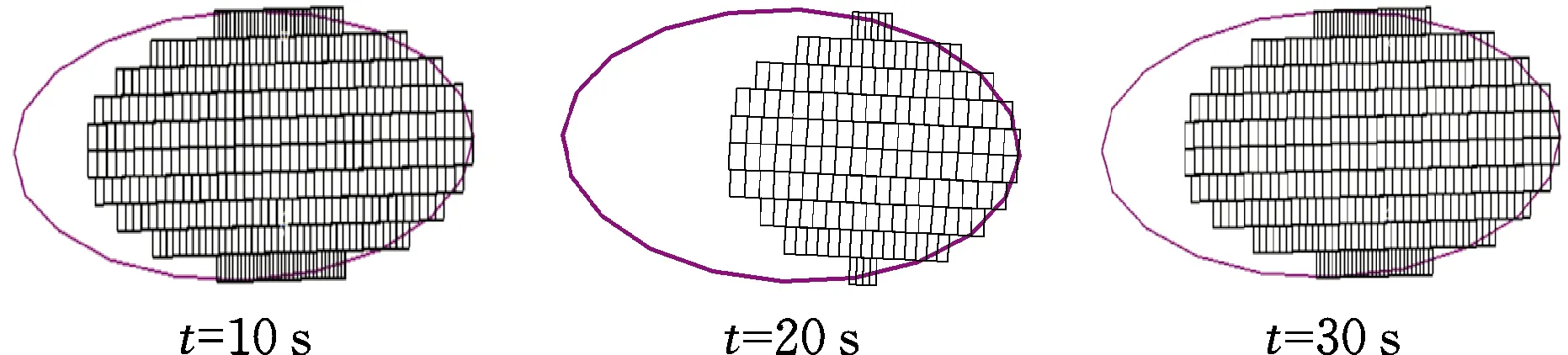
(a) v0=130 km/h

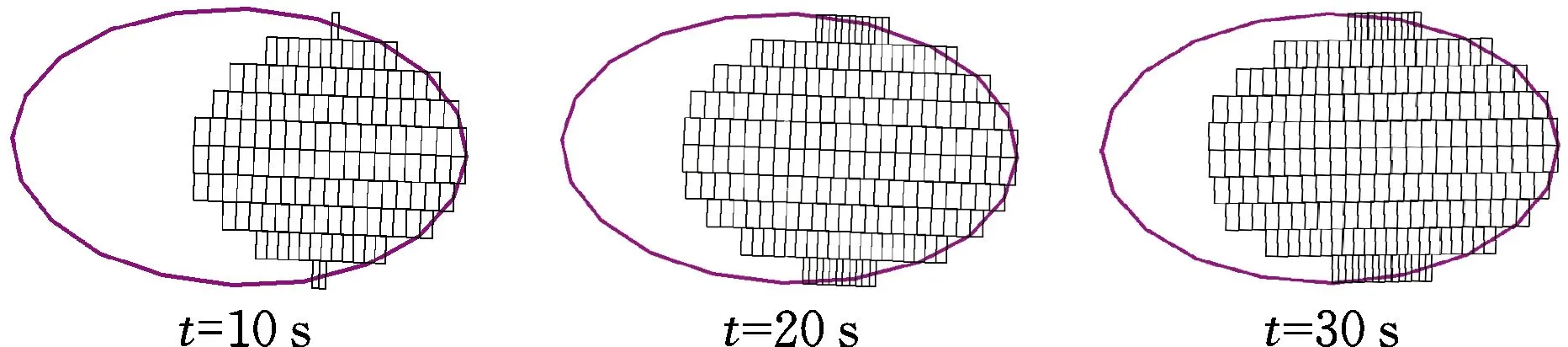
(b) v0=160 km/h

图20 制动速度为130 km/h时接触斑内最大滑移量Fig.20 Maximum slip in the contact spot at a braking speed of 130 km/h

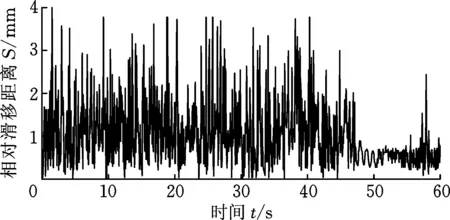
图21 制动速度为160 km/h时接触斑内最大滑移量Fig.21 Maximum slip in the contact spot at a braking speed of 160 km/h

通过式(9)、式(10)可计算出轮轨摩擦区及闸瓦摩擦区踏面累积磨损深度，如图22所示。制动初速度为130 km/h时，闸瓦摩擦区与轮轨摩擦区内最大累积磨损深度分别为1.70 μm、4.2 μm；制动初速度为160 km/h时，闸瓦摩擦区与轮轨摩擦区内最大累积磨损深度分别为2.11 μm、5.32 μm。文献[5] 以轴质量为20 t、闸瓦压力为30 kN、初始速度为130 km/h和160 km/h两种制动工况在轮轨滚动的基础上进行了循环制动40次的踩刹车试验，最终得到两种制动初速度下车轮踏面轮廓磨损演化过程。文献[5]的试验结果表明位于轮轨接触区内的踏面磨损较为严重，当初速度为130 km/h时循环制动40次之后踏面最大磨损深度达到0.15 mm，那么平均每一次制动磨损深度约为3.75 μm。本文通过仿真得到单次制动最大磨损深度为5.90 μm，其值约为文献[5]试验值的1.31倍，如图23所示。文献[5]中，当初速度为160 km/h时，循环制动40次之后踏面最大磨损深度达到0.20 mm，那么平均每一次制动磨损深度约为5 μm，相对应地，本文通过仿真得到单次制动最大磨损深度为7.43 μm，其值约为文献[5]试验值的1.49倍。

1.轮轨摩擦区(vt=130 km/h) 2.闸瓦摩擦区(vt=130 km/h)3.轮轨摩擦区(vt=160 km/h) 4.闸瓦摩擦区(vt=160 km/h)图22 闸瓦区磨损深度与轮轨间磨损深度对比Fig.22 Comparison of the wear depth between the brake shoe area and the wheel-rail wear depth

1.vt=130 km/h 2.vt=160 km/h图23 车轮踏面总的磨损深度Fig.23 Total wear depth of the wheel tread

文献[13]通过单轴拉伸试验对U75VG钢轨材料进行高温疲劳损伤试验，在不同温度下U75VG钢均表现出明显的棘轮效应，尤其当温度升高时，在塑性-蠕变交互作用下，棘轮行为演变速率呈加速趋势。并且在300 ℃时应变强化显著增强，从而导致车轮材料在宏观上呈现出硬化现象(弹性模量、屈服强度、抗拉强度均增大)；在600 ℃时，表现出明显的循环软化现象。从以上结论中推导出U75VG钢材料的高温软化与应变强化间存在一定的竞争关系。由于车轮钢材料同样属于应变硬化材料，车轮踏面经过反复碾压，在温度与应变强化综合作用下，表现出循环硬化现象，使磨损更不容易发生，因此试验所测得磨损深度小于仿真计算深度。