转轴转速波动信号的时频脊线提取方法
2021-02-28龚思琪李舜酩庾天翼
龚思琪,李舜酩,庾天翼
(南京航空航天大学 能源与动力学院,南京 210016)
变转速是旋转机械设备的常见复杂工况,其核心旋转零部件在变转速工况下的故障振动信号具有明显的非平稳特点[1]。基于振动信号处理的故障诊断方法对设备状态监测和故障诊断都至关重要[2]。
传统的基于振动信号处理的故障诊断方法大多以不同状态下的时域、频域及时频域信息作为参考,通过对它们的统计特征指标对比分析设备当下的健康状态及潜在的故障特征[3-4]。在变转速下的故障振动信号的信号表征与故障模式之间的对应关系更复杂,导致传统的傅里叶变换并不能完全揭示变转速信号的局部细节特征。在近20年来,随着非平稳信号处理理论的发展和电子硬件计算技术的快速成长[5],对变转速下机械设备动态信号处理及故障诊断方法开展了广泛的研究。研究者对小波变换[6]和高精度的频谱与时频分析方法[7-8]等故障诊断技术进行了广泛研究,并综合运用统计物理学方面的信号特征提取方法[9]、盲源分离方法[10]、变分模式分解[11]等方法提高诊断准确率。瞬时频率变化脊线是振动信号的重要特征之一。通常利用峰值检测法提取时频脊线[12],文献[13]提出了非线性挤压时频变换方法提取旋转机械故障振动信号中的多分量非稳态信号。但在受到强噪声干扰的变转速工况下的振动信号时频脊线提取和瞬时转速提取时,准确率较低,辨识效果较差[13],且对于含有多个频率分量的信号,脊线难以辨别。文献[14]提出了一种双向搜索时频脊融合方法,提取时频变工况行星齿轮箱高速轴的瞬时转速,可靠性高,但程序编写困难,工作量大,而且需要丰富的理论知识。
针对噪声干扰下的变转速旋转机械振动信号时频脊线提取和冲击特征识别问题,本文在利用短时傅里叶变换得到转速波动信号的时频分布图;再将其沿时间轴分割,利用提取中心频率的方法逐段提取时频脊线;然后,利用卡尔曼滤波技术提取整段信号的最优脊线。通过分析脊线特点,可以准确有效地判断转子故障发生的时间。进一步,利用本文所提方法提取含有多个频率分量信号的时频脊线特征;最后,利用变转速故障轴承的振动信号验证本文所提方法的有效性和准确性。结果表明:所提方法的时频脊线提取准确率高,操作简单,易于实现,对转速波动信号的特征提取有重要的参考价值。
1 转轴故障振动信号的频谱分析
1.1 实验信号采集
本研究所使用的试验台如图1所示,由电机驱动,在600~1 500 r/min的转速下工作,采用油脂润滑。驱动电机的额定功率为0.75 kW,额定电压为380 V,额定转矩是5.0 kN·m。

图1 传动轴变转速故障振动试验台及传感器放置位置
为了测量转轴在变转速下的振动信号,在转轴驱动端和输出端各安装一个振动三向加速度传感器采集传动变转速振动信号,传感器安装位置如图1(a)、(b)所示。本次变转速以匀加速方式实现,使电机以600 r/min的转速开始工作,匀加速至1 500 r/min。测试所用的振动传感器型号和基本参数如表1所示。

表1 振动传感器的基本参数
在试验过程中,采用LMS振动信号采集系统采集被测转轴的故障振动信号。根据转速和采样频率可知信号一个周期,即试验转轴旋转一周所采得的数据点个数为2 048~5 120。
在测试过程中,选择5 s内的振动信号作为分析目标,测试得到的变转速转轴的不平衡故障振动信号波形如图2所示。
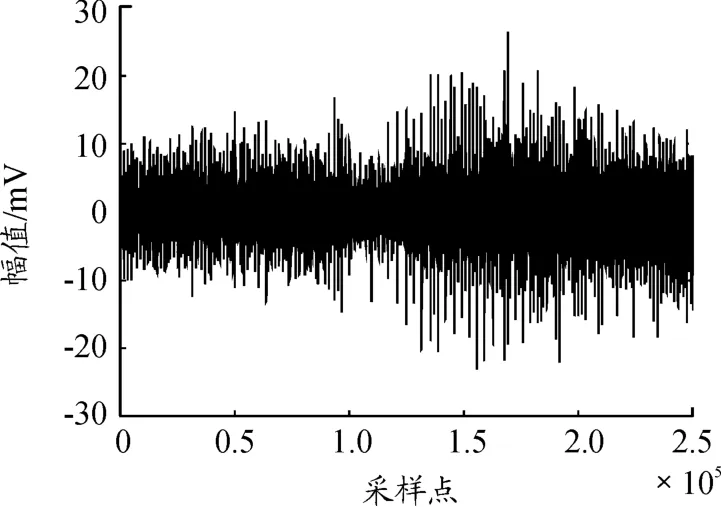
图2 转速波动信号时域波形
1.2 信号的频谱特点
根据式(1)所示的傅里叶变换(fourier trans form,FT)公式,通过改进可将信号通过快速傅里叶变换,得到图3所示的转速波动信号的频谱图。
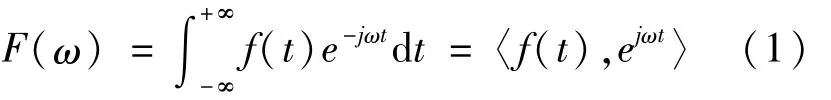
从图3转速波动信号的频谱图可以看到:信号主要集中在小于1 000 Hz的范围内,并伴有噪声干扰,可以看到频率在0~400 Hz出现了最大幅值,且有多个频率分量。

图3 转速波动信号的频谱图
2 信号的时频分析
根据式(2)所示的短时傅里叶变换(short time fourier transform,STFT)的表达式,可得到时频分布图。
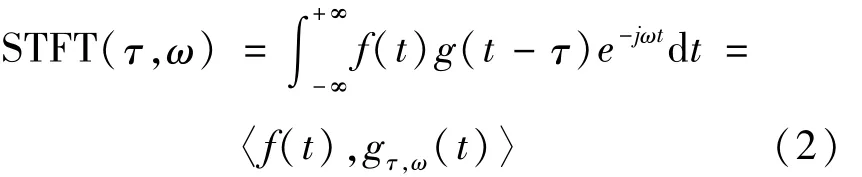
式中:STFT(t,w)表示STFT分析结果;f(t)为待分析信号;g(t)表示STFT窗函数。
窗口函数g(t)的选择决定了分辨率的高低。根据不同窗函数的特点可知:具有带通特性的汉宁窗或汉明窗虽然对信号滤波有更好的效果[15],但是会使能量几乎集中在主瓣。而高斯窗函数可以取得时间和频率分辨率的最佳折衷[16]。因此,选取高斯窗函数对信号进行STFT。
对变转速故障振动信号进行STFT分析,得到如图4所示的二维时频图。可以看出:频率在0~1 000 Hz和4 000 Hz附近的能量高,频率随时间基本保持不变,它们是由转子的固有振动模态引起的。但在6~15 s的时间范围内,如图4中的频率线2和3以及它们附近的多个频率出现了随时间变化而不断上升的趋势。这表示随着采样时间的增加,转轴的转动频率也逐渐增加,这是由于转子在6~8 s产生波动导致的频率沿采样时间的增加而升高。
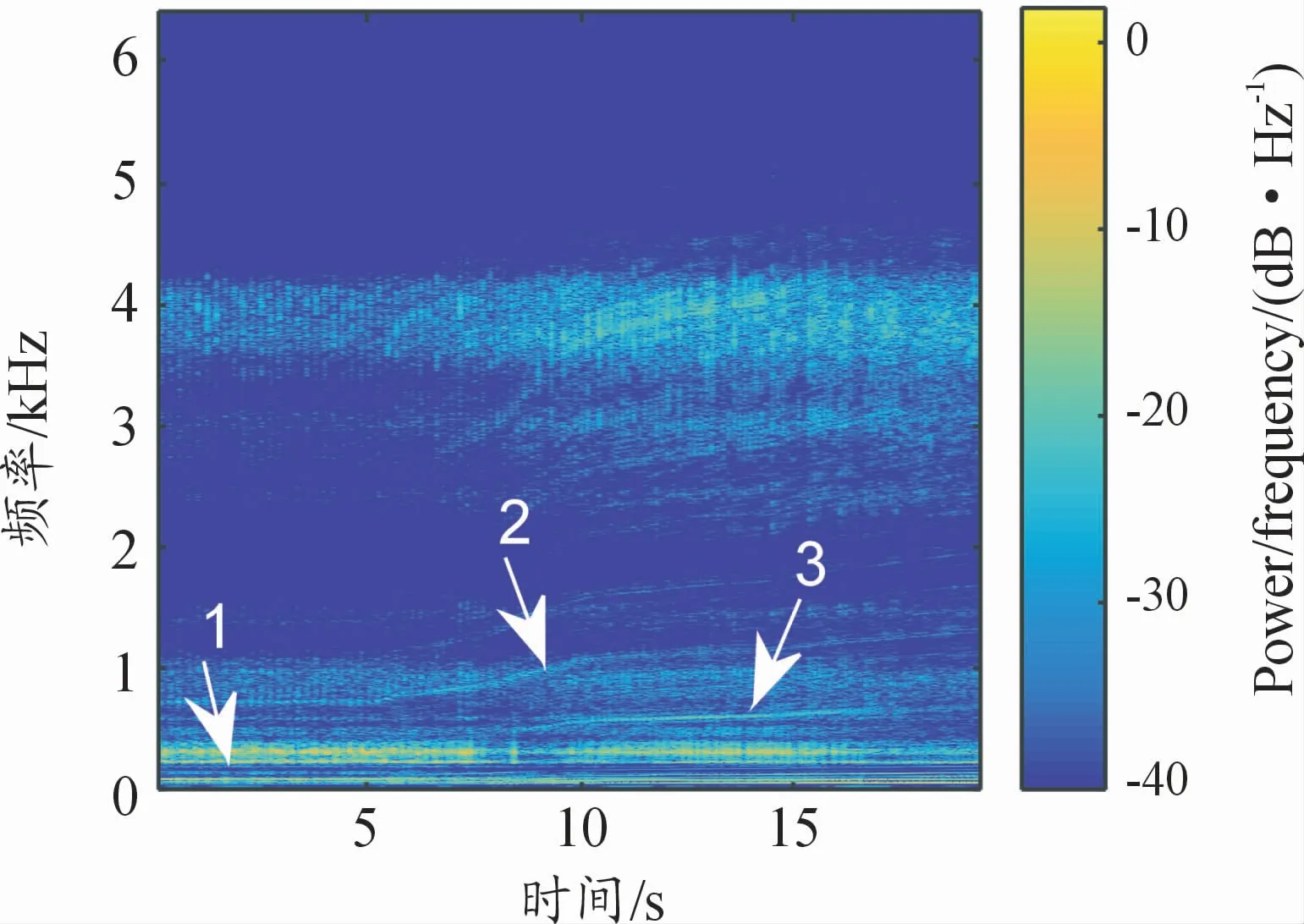
图4 转速波动信号的二维时频图
由于转子转速在600~1 500 r/min波动,转子转频最高在25 Hz附近,通过图3的转速波动信号的频谱图可以判断转速波动信号的频率主要集中在0~400 Hz。从图5可以看到:频率不随时间变化的线4,以及在时间大于8 s时,频率随时间变化的线5、线6。其中,线4的频率是56 Hz,大约是转子频率的3~4倍。

图5 时频图4的局部放大图
3 信号的脊线提取
对信号进行STFT后,一些与机械系统零部件的动力学特性相关的曲线会清晰或隐约地出现,这些曲线在三维空间内的分布形态与“山脊”很像,是脊线标志或沿脊顶延伸的线。因此,在时频图中把三维空间内沿功率最高点延伸的线称之为时频脊线[17],表现在时频面上,是明亮程度和趋势各异的线条,它能够表征信号频率变化的各种模式[18]。
信号在时域和频域的能量可表示为:
能量分布还满足边缘性质:

从时频表示上直接提取的时频脊线受噪声影响大,脊线特征不明显,从峰峰值上得到的脊点,噪声难以消除,导致所需提取的脊线淹没在噪声的峰值点中,如图6所示。
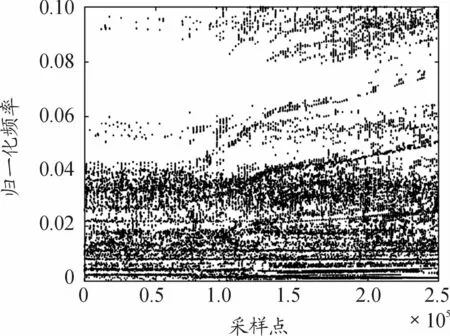
图6 转速波动信号提取时频脊线
从时频能量最高点上提取信号的中心主频率,遍历时间轴,会得到图7中的线1、2、3。在0~6 s的时间段内,转速波动信号的频率主要在56 Hz附近有小范围的波动;在6~9 s时间段内,中心频率与时间的关系变得很复杂;在9~12 s时间段内,中心频率集中在二阶频率分量处有上升趋势;在12~20 s的时间段内,中心主频率在25 Hz附近随着时间的增加而升高;在12 s处频率有突变,如图7中区域3所示。导致这种突变产生的主要原因是在6~8 s时间段内产生故障后,信号的频率分量与能量的对应关系模糊,使得部分频率分量的能量突然间提高,而其他频率分量的能量降低。
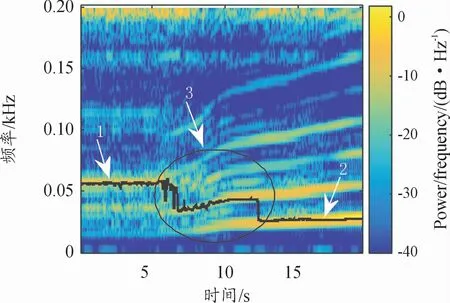
图7 转速波动信号脊线图
时频面内脊线附近局部区域内的时频点能量突出,具有相对较高的信噪比,机械系统运行过程中状态一般不会出现突变,出现的时频脊线具有连续平滑的特点。因此,直接通过能量最高点来提取时频脊线的方法失效。但该方法表示出了该转速波动信号的能量变化,为后面沿时间域分割信号的分割点提供了依据。
根据脊线过渡平滑的特点,以及图7直接提取的中心频率的剧烈变化,将提取区域按时间划分为3个部分:0~6 s,6~9 s,9~20 s。目标频率范围设置为(f-Δf,f+Δf),Δf=5 Hz由于转子的转速为600~1 500 r/min,将图7中线2的12~20 s所示的脊线即表示一阶频率作为即将要提取的目标脊线,通过对时间轴分段提取,将提取的频率阈值设置在接近一阶中心频率附近,再根据能量最高点提取频率范围内的曲线。
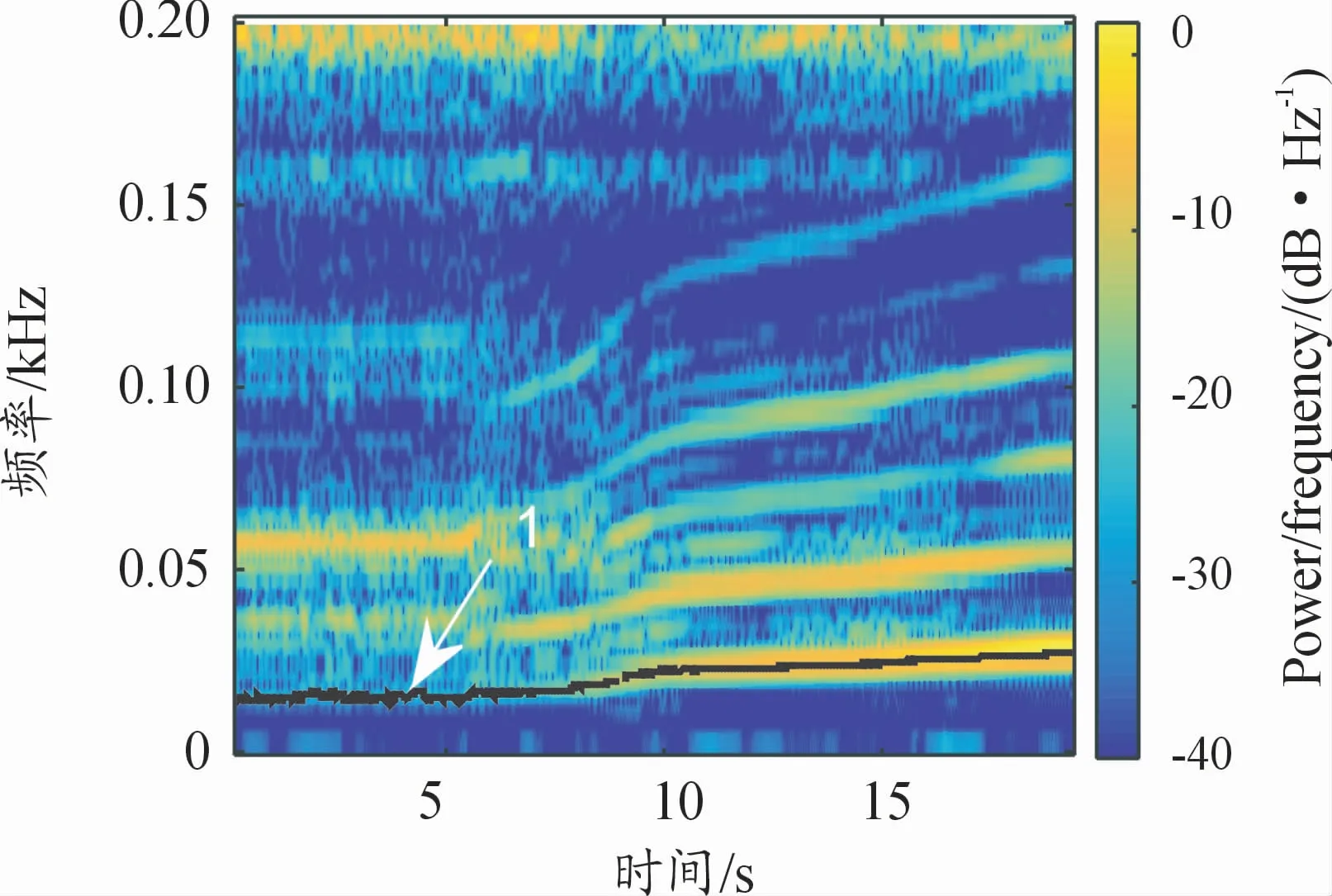
图8 转速波动信号目标脊线
由图7的信号脊线图可以看出:56 Hz的频率大概是转速信号的3~4倍频。由此可推算出:一阶频率在14 Hz附近,在0~6 s将目标频率f设置为14 Hz,6~9 s频率变化范围大,且初步确定是转速增加的,故将目标频率设置为f=18 Hz。9~20 s也是一个转速上升的过程,但相比第2段,其过渡较为平稳,最高转速1 500 r/min,频率为25 Hz,将其目标频率设置为f=25 Hz,得到如图8线1所示的脊线。
从图8中的线1可以看到:在0~5 s目标脊线在这一时间段的频率随时间波动比较剧烈,结合图7中该段时间内的能量集中在56 Hz附近,因此在图8中该段时间内在该处能量比较分散会引起较大的波动。目标脊线在5~10 s之间的过渡十分复杂,时间在10~20 s之间的目标脊线波动较小,但频率随时间增加的趋势也更为明显。
4 最优脊线提取
卡尔曼滤波器是一种最优化自回归数据处理算法,对于解决很大部分问题都会是最优、效率最高甚至是最有用的[20]方法。因此,本文采用卡尔曼滤波在时频面内提取目标脊线的最优脊线[21]。
Kalman滤波器的系统测量值、状态运动方程和观测方程分别为[22]:
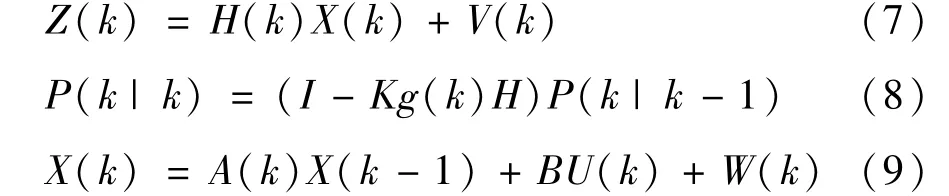
式中:X(k)是k时刻的系统状态;U(k)是k时刻对系统的控制量;A是状态转移矩阵;Z(k)是k时刻的观测值;H是观测矩阵;W(k)和V(k)表示上述两个方程中的噪声。
在实际问题中,通常假设A(k)=A,H(k)=H。设W和V为噪声(white gaussian noise),协方差分别为Q,R(这里假设它们不随系统状态变化而变化)。首先,利用状态方程预测下一状态的系统。假设当前时刻为k,根据系统的模型,可以基于系统的上一状态而预测出现在状态:
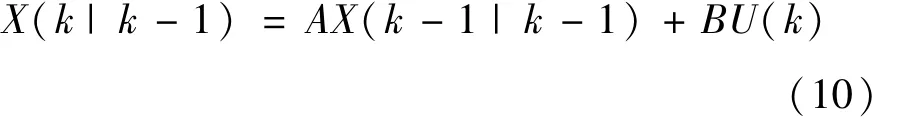
式中:X(k|k-1)为利用上一状态的预测结果;X(k-1|k-1)为上一状态的最优结果;U(k)为现在状态的控制量,若没有控制量,它可以为0。
对应于X(k|k-1)的协方差,即上面预测值相对于真实状态的误差方差阵更新公式为:

式中:P(k|K-1)是X(k|k-1)对应的协方差;P(k-1|k-1)是X(k-1|k-1)对应的协方差;A′表示A的转置矩阵;Q是系统过程的协方差。
当第k时刻的观测值Z(k)到达以后,利用预测值中没有的信息去修正第k个时刻的状态预测值。结合预测值和测量值,可以得到状态(k)时最优化估算值X(k|k):

式中,Kg为卡尔曼增益(Kalman Gain),可通过式(13)估计:

为了使Kalman滤波器运行直到系统过程结束,需要更新k状态下X(k|k)的协方差:
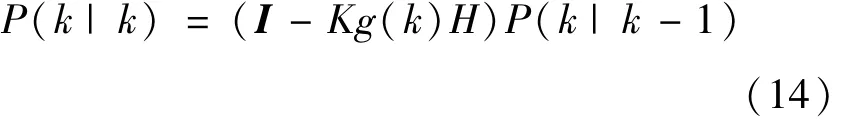
式中,I为单位矩阵,对于单模型单测量,I=1。当系统进入k+1状态时,P(k|k)就是式(11)的P(k-1|k-1)。
通过以上卡尔曼滤波器的5个核心公式不断进行迭代优化运算,可以完整实现Kalman滤波。将原始脊线的初始坐标作为卡尔曼滤波的初始状态输入,将P的初值设为1,保证卡尔曼滤波能够稳定运行。通过多次试验可得协方差Q与R分别为10-8,10-5时,Kalman滤波的滤波效果最佳。根据脊线平滑且表示信号的频率随时间变化趋势的特点,得到图9所示的转速波动信号的最优目标脊线。图9中蓝色曲线表示经过沿时间轴分割后提取的原始脊线,红色曲线表示经过卡尔曼滤波技术后得到的最优脊线,橙色曲线表示两曲线之间的误差。为了使脊线信息更加明显,将纵坐标范围缩小至0~45 Hz。相比原始脊线,最优脊线更加平滑,且其表达的频率随时间变化的趋势没有改变。在0~4 s时间段内,可以看到经卡尔曼滤波器提取的脊线频率更加集中,这也更加真实地反映了在这段时间内转子正常运转。而误差曲线主要集中在0 Hz附近,说明最优脊线与实际信号误差小,最优脊线能反映实际信号波动情况的真实信息。
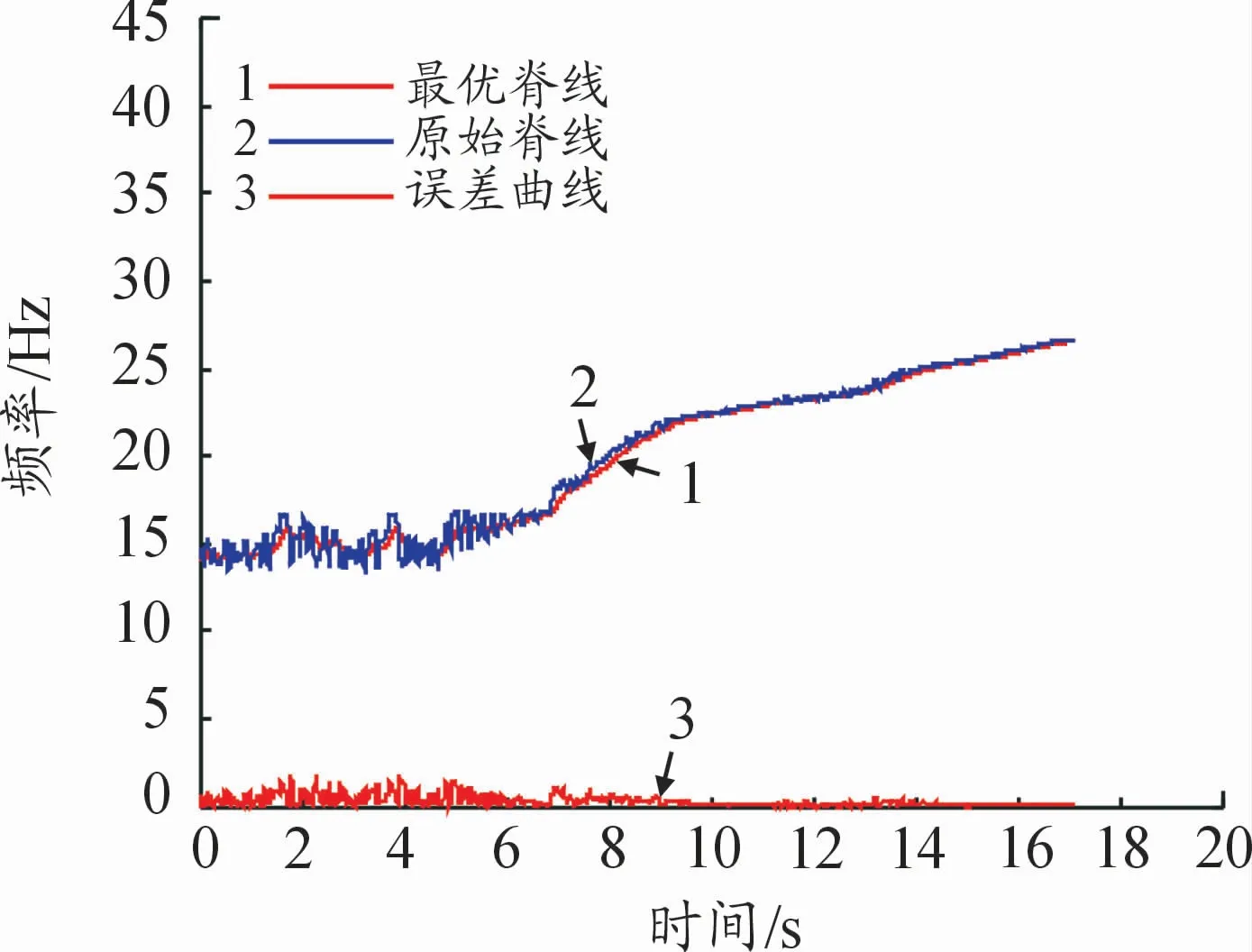
图9 转速波动信号最优脊线
5 结论
1)在STFT时频分析的基础上,结合能量最高点提取中心主频率的方法,提取转速波动信号的时频脊线,可以观察到信号频率在不同时刻发生的变化,并可以判断转子系统是否发生故障以及故障发生的时间。相比直接提取时频脊,其所受噪声影响更小。
2)通过对不平稳信号的时频脊线进行卡尔曼滤波,可以有效地找到目标脊线的最优解,得到表达信号频率随时间变化的趋势的平滑的时频脊线。
3)通过对转轴试验台实测信号变换结果的观察分析可知:从故障振动信号的时频谱图提取时频脊线,并利用卡尔曼滤波估计最优脊线,可以有效地滤除背景噪声,剔除干扰分量,得到平滑且清晰的时频脊线。
