基于Hansel Spittel模型的齿环用HAl61 4 3 1合金本构模型构建

尹小燕，骆 静，朱 杰

（1．成都理工大学工程技术学院，四川 乐山 614000；2．江苏科技大学 材料科学与工程学院，江苏 镇江 212000）

齿环是变速箱中同步器的重要组件，齿环的质量直接影响换挡顺畅与否，也很大程度上决定了同步器的性能［1］。齿环工作状态时承受较大的摩擦力矩，摩擦剧烈，因此齿环一般采用高强耐磨耐蚀的复杂黄铜合金制造。

HAl61 4 3 1合金是近年来新开发的一种高强耐磨复杂黄铜合金，主要用于制造轿车同步器齿环。铜制齿环的加工工艺为“热精锻＋机械车削”［2］。因此，研究HAl61 4 3 1合金的高温流变行为及构建高精度的本构模型是制定合理热加工工艺和有限元分析的关键。近年来国内外在此方面的研究十分活跃，肖铁忠等［3－4］基于数值模拟分析优化了铜合金齿环的热精锻成形工艺，王梦寒等［5－7］基于数值模拟改进了多款铜制齿环热精锻的成形缺陷，赵祥伟［8］研究了HAl61 4 3 1合金在干摩擦条件下的摩擦磨损性能，张全叶等［9］研究了变质剂对HAl61 4 3 1铸态组织性能的影响。目前，对齿环热锻成形工艺及工艺参数优化、HAl61 4 3 1合金耐磨性能的研究较多，而对HAl61 4 3 1合金热流变行为及其有限元应用的研究较少。因此，以HAl61 4 3 1合金为对象，研究该合金的高温流变行为，基于Hanse Spittel模型构建该合金的本构模型，应用该本构模型进行数值模拟并研究该模型的准确度，为后续齿环精锻数值模拟分析提供材料模型基础。

1 实验方法及结果分析

实验材料为齿环用挤压态HAl61 4 3 1合金，其化学成分如表1所示，金相组织如图1所示，组织为β相＋α相＋强化相，基体为β相，α相呈针条状，Co－Ni－Fe－Si强化相多呈颗粒状、少量呈块状均匀分布。在实验管材上截取尺寸规格为φ8×12 mm的试样，在Gleeble 3500热模拟试验机上进行等温热压缩实验，试样以10℃／s的速率加热至不同变形温度（600、650、700、750、800℃），然后以不同应变速率（0．01、0．1、1、10 s－1）进行等温压缩，压缩变形量为60%，共计20组实验。实验结束后立即水淬至室温。

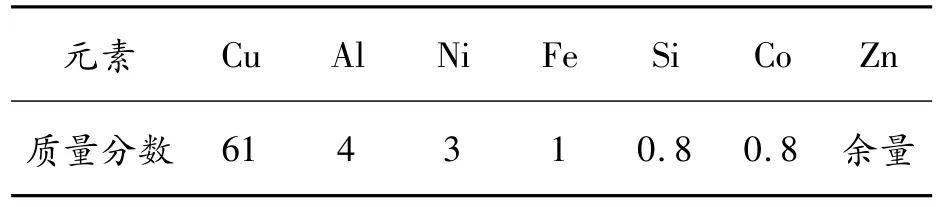
表1 HAl61 4 3 1合金的化学成分 （wt／%）

图1 HAl61 4 3 1合金挤压态微观组织

图2 为不同变形温度、不同应变速率下HAl61 4 3 1合金的真应力 －应变曲线。由图2可知，材料的流变应力与变形温度、应变速率和应变有关。流变应力随着应变的增加先快速增加，后逐渐趋于平稳，这是由于变形初期发生加工硬化，流变应力值快速上升，而随着变形量增加，动态软化与硬化效应逐渐趋于动态平衡，流变应力值趋于平稳。在应变速率一定时，变形温度升高，流变应力明显下降，这是因为温度升高有利于发生位错的滑移和攀移，提高了塑性，从而使流变应力降低。在变形温度一定时，应变速率增加，流变应力明显上升，这是因为应变速率提高，动态再结晶所需的孕育时间不足，动态再结晶来不及发生，从而流变应力升高。

图2 HAl61 4 3 1合金在不同条件下的真实应力－应变曲线

2 本构模型的建立

HAl61 4 3 1合金主要被用于齿环制造，了解该材料的高温流变行为及构建相应的本构模型可为后续的数值模拟进行指导。因此，采用Hansel Spittel模型［10－13］构建HAl61 4 3 1合金的高温本构模型，Hansel Spittel模型适用于热 －黏性材料的稳态应力与应变速率和温度之间的关系，也可描述任意应变水平下流变应力与应变速率之间的关系。其模型表达式为

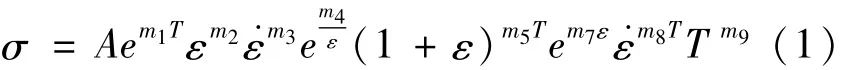
式中：σ为流变应力；A为材料常数；e为自然常数；T为变形温度；ε为应变； ε为应变速率；m1为温度相关系数；m2为应变强化指数；m3为应变速率强化指数；m4为应变软化系数；m5为温度相关应变强化系数；m7为应变相关系数；m8为温度相关应变速率强化指数；m9为温度指数。

对式（1）取对数，可表达为

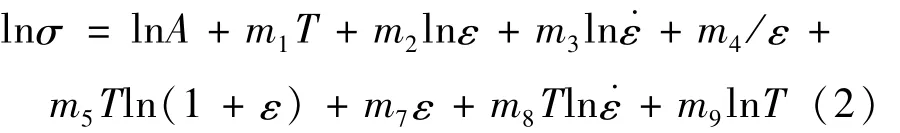
2．1 m3和m8值的求解

当温度和应变为一定值时，ln A＋m1T＋m2lnε＋m4／ε＋m5T ln（1＋ε）＋m7ε＋m9ln T为常数，设为L1，故式（2）可转化为式（3）

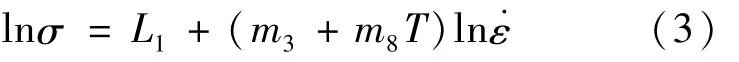
将4个应变率和5个变形温度下应变为0．02～0．88、间隔为0．02的应力数据点分别代入式（3），绘制每个温度下ln ε和lnσ的散点图，并进行线性拟合，如图3（a）（b）所示为变形温度为600、700℃的拟合曲线，其余温度计算方法相同。其中得到的5个温度下，44个应变拟合直线斜率的均值即为对应温度下的S1（S1＝m3＋m8T）的值。绘制44个应变条件下，S1和温度T的散点图，并进行线性拟合，如图3（c）所示，拟合直线的截距和斜率的算术平均值分别对应m3和m8。

2．2 m1、m5和m9值的求解

当应变速率和应变为一定值时，ln A＋m2lnε＋m3ln ε＋m4／ε＋m7ε为常数，设为L2，故式（2）可转化为

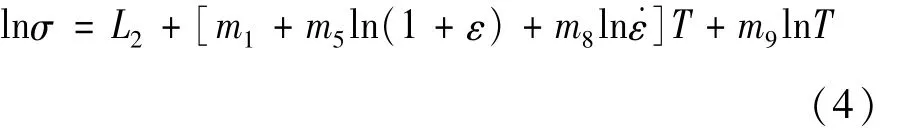
令S2＝m1＋m5ln（1＋ε）＋m8ln ε，将4个应变率和5个变形温度下应变为0．02～0．88、间隔为0．02的应力数据点以lnσ＝S2T＋m9ln T＋L2形式进行拟合，如图4（a）（b）所示为 ε＝0．1 s－1和 ε＝1 s－1下的拟合结果，其余应变速率计算方法相同。将得到的4个应变速率下：44个应变拟合的m9求均值即为对应的m9，同时可得到不同应变速率下的S2值。绘制4个应变速率下，ln（1＋ε）和S2的散点图并进行线性拟合。如图4（c）所示为 ε＝0 1 s－1和 ε＝1 s－1下的拟合结果，拟合直线斜率的算术平均值为m5，由截距则可计算得出m1值。

图3 m3和m8系数求解过程曲线

图4 m1、m5和m9系数求解过程曲线

2．3 m2、m4、m7和A值的求解

当应变速率和温度为一定值时，ln A＋m1T＋m3ln ε＋m8T ln ε＋m9ln T为常数，设为L3，故式（2）可转化为

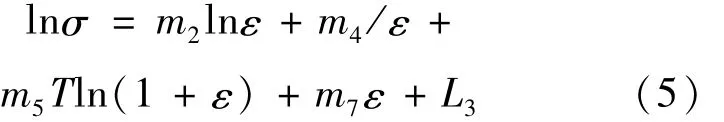
对4个温度，不同应变速率下应变为0．02～0．88、间隔为0．02的lnσ与 ε的关系用式（5）进行拟合，如图5所示为600、700和800℃的拟合曲线，其余温度计算方法相同。通过拟合可得到不同温度下的拟合系数，求算术平均值即为m2、m4和m7的值。

将实验所得数据及以上所求的m1－m9的值分别代入式（1），即可求得不同变形条件下的A值，将所求得的值求算术平均值即为模型A值。计算和拟合得到的各参数如表2所示，将参数代入式（1）可得到HAl61 4 3 1合金的本构模型，如式（6）所示。根据该式可获得不同变形条件下流变应力预测值，如图6所示，由本构模型预测的流变应力与实验结果吻合度较好。

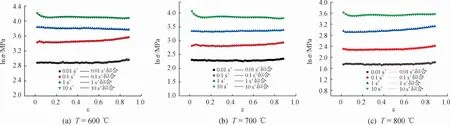
图5 lnσ－ε的线性拟合曲线

表2 HAl61 4 3 1合金Hansel Spittel模型各材料参数值

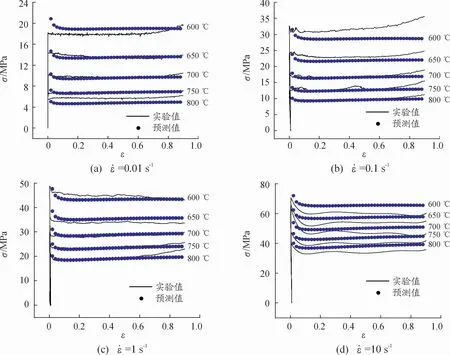
图6 基于Hansel Spittel模型的不同变形条件下的预测值与实验值

3 本构方程的验证

为了验证模型的预测精度，引入2个统计参数指标，即相关系数R（式（7））和平均相对误差AARE（式（8））对模型的预测能力进一步评估，同时将4个应变速率和5个变形温度条件下，应变范围0．02～0．88、间隔0．02的模型预测应力值与相应的实验应力值绘制在同一坐标系，如图7所示。

图7表示Hansel Spittel模型的流变应力预测值与实验值之间的相关程度，45°直线表示预测值与实验值之间的最佳回归线。由图7可见，大部分数据点都分布在直线上，相关系数为0．994 1，说明预测值与实验值呈紧密的线性关系。Hansel Spittel模型的平均相对误差为6．042 8%，说明模型预测精度较好，能反映HAl61 4 3 1合金高温塑性流变行为。

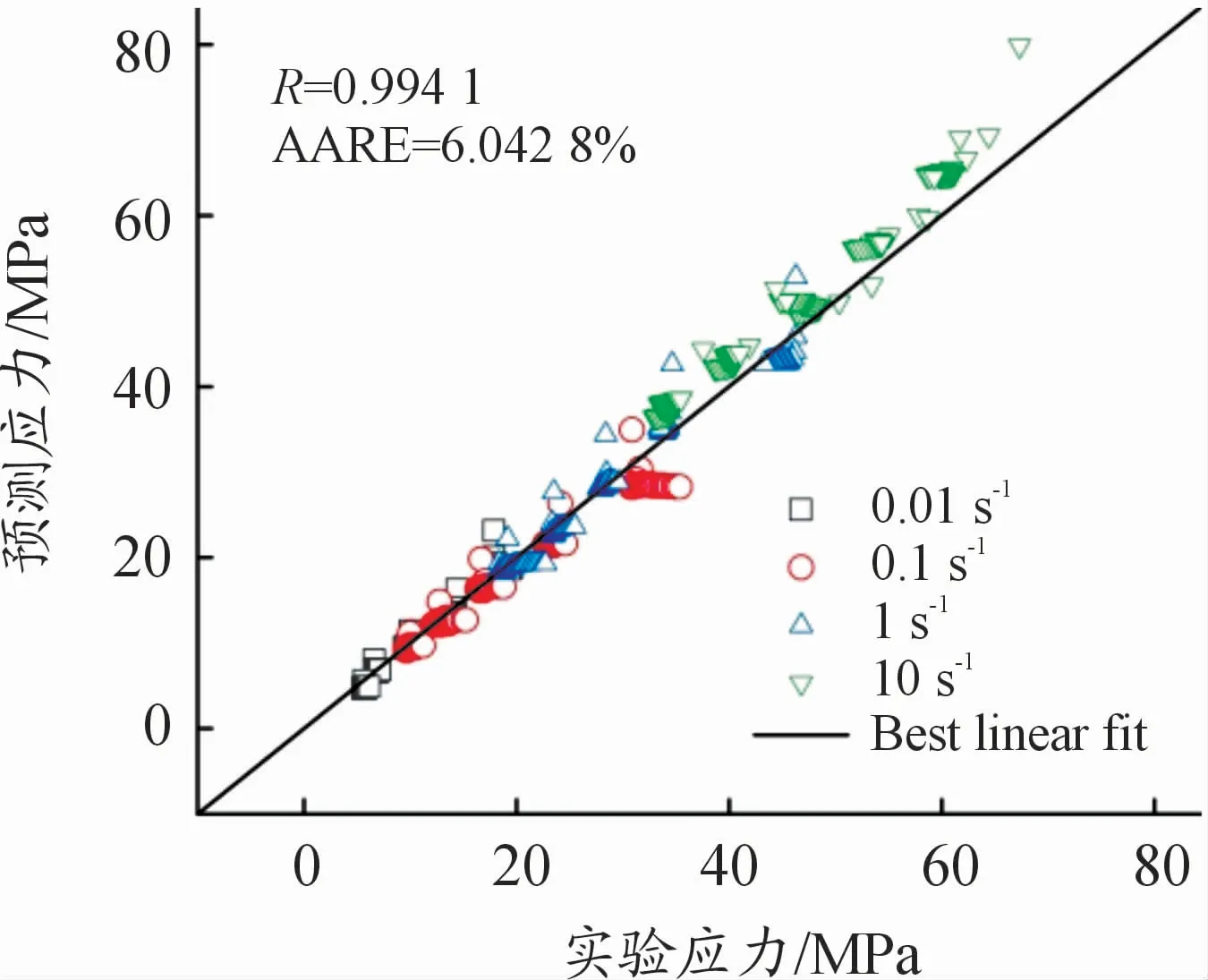
图7 预测值与实验值之间的相关性曲线

为进一步验证在有限元模拟中所建立本构模型的准确性，将建立的HAl61 4 3 1合金Hansel Spittel本构模型导入锻造成形有限元软件FORGE［14－15］中，数值模拟20组等温热压缩实验，并分别导出成形力－位移曲线，模拟参数见表3。不同变形温度和应变速率下的数值模拟与实验结果的力－位移曲线，如图8所示。总体来看，数值模拟的力－位移曲线与实验结果曲线较吻合。

表3 模拟参数

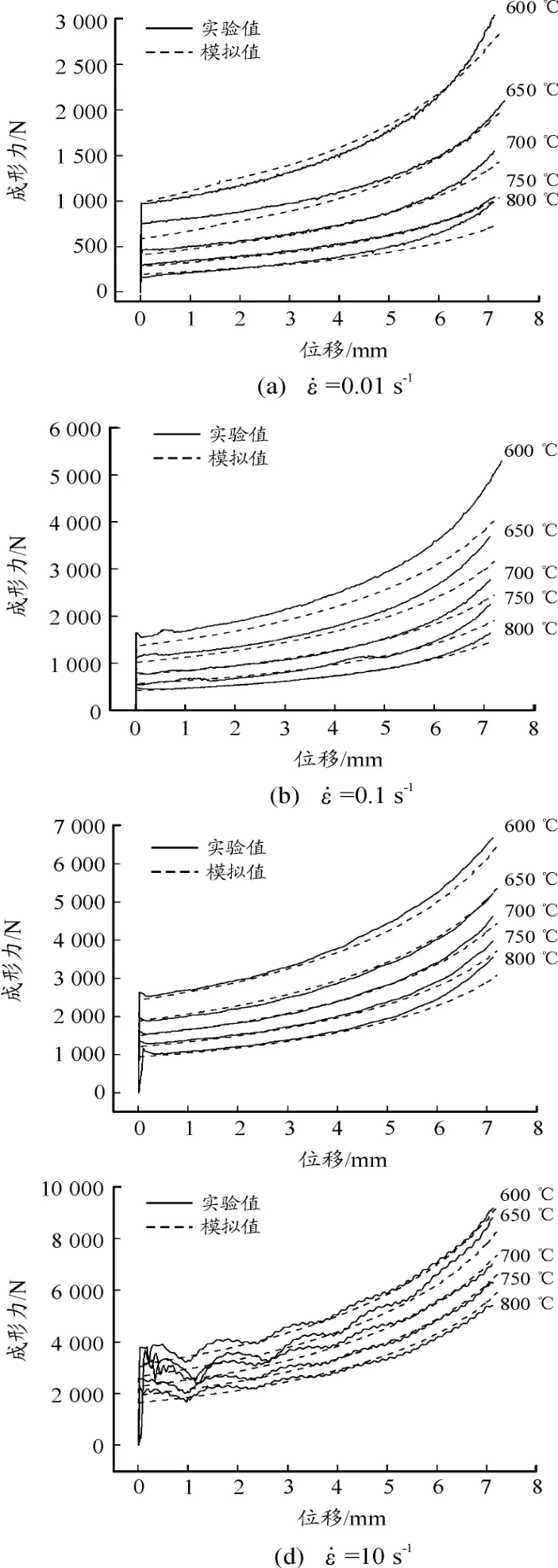
图8 不同变形条件下数值模拟与实验结果 力－位移曲线

表4为不同变形条件下实验值与模拟值的平均相对误差，最大误差为600℃＆0．1 s－1条件下的12．35%，最小误差为700℃＆1 s－1条件下的1．12%，总误差为4．6%，说明所建立的HAl61 4 3 1合金Hansel Spittel本构模型可以应用于有限元模拟中，并且精度较高。

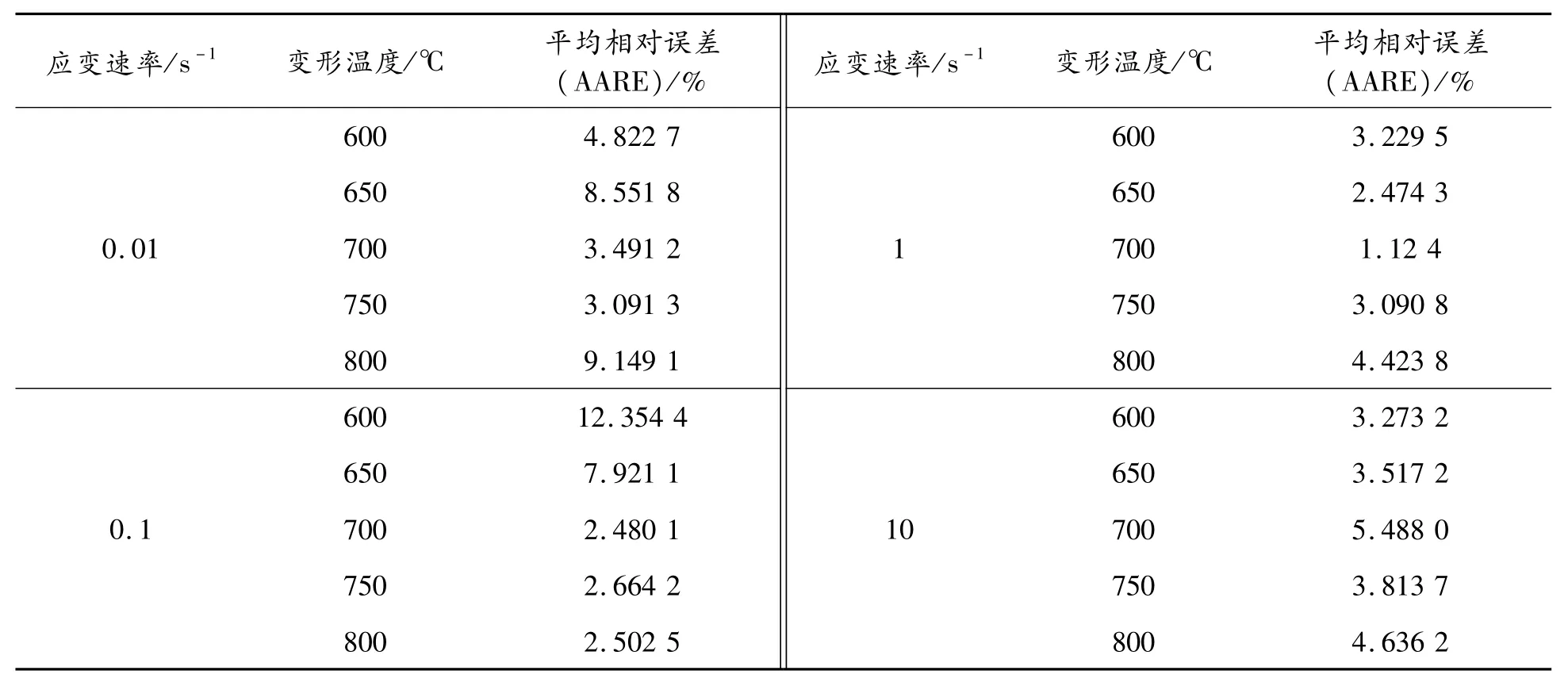
表4 不同变形条件下实验值与模拟值的平均相对误差

4 结论

1）通过等温热压缩实验获得了HAl61 4 3 1合金在变形温度600～800℃、应变速率0．01～10 s－1下的真应力 －应变曲线，实验结果表明：HAl61 4 3 1合金的流变应力与变形温度、应变速率和应变呈非线性关系，并且与变形温度呈负相关、与应变速率呈正相关。

2）以真应力－应变数据为基础，建立基于Hansel Spittel模型的HAl61 4 3 1合金本构模型，量化结果表明：基于Hansel Spittel本构模型的预测值与实验值的平均相对误差为6．042 8%，相关系数为0．994 1，说明模型的预测精度较高，可以用于后续的有限元模拟分析。

3）将Hansel Spittel本构模型应用于等温热压缩数值模拟，并以数值模拟和实验结果的成形力－位移曲线进行对比分析，结果表明：数值模拟的力－位移曲线与实验结果曲线基本吻合，总误差为4．6%，为后续齿环的精密塑性成形有限元模拟提供数据支撑。