基于磁链观测的IPMSM MTPA控制系统研究
2021-02-28张娜娜沈艳霞
张娜娜,沈艳霞
(江南大学 物联网工程学院,无锡 214122)
0 引 言
内置式永磁同步电机(以下简称IPMSM)的凸极特性使其具有体积小、功率密度大、输出转矩能力强和可调转速范围宽等优点[1],在电动车、电动工具、数控系统及白色家用电器等领域得到了广泛应用。随着电动产品控制技术的不断发展,人们对节能减排的要求越来越高,优化电机控制策略以降低电能消耗成为电动控制领域不断研究的课题[2-3]。在此背景下,由于IPMSM的最优转矩电流比(以下简称MTPA)控制可以使电机在单位电流下提供最大电磁转矩,提高系统的能源利用率,因此得到很多研究者的青睐[4-6]。用于IPMSM的MTPA控制需要以获得精确的转子位置为基础,但考虑到驱动系统的成本、工作的稳定性及实体传感器装配的困难,传统的位置检测方式逐渐被无位置传感器技术取代。在此背景下,磁链观测器法以其在中高速范围性能优越的表现,在保证系统稳定性的同时,最大位置检测误差可以控制在1°范围内[7]而受到青睐和广泛研究。
IPMSM电机的电磁转矩由两部分组成,即同步转矩Tes和磁阻转矩Ter。同步转矩由转子永磁体和电枢电流q轴分量的相互作用产生,磁阻转矩由不对称的电机结构产生。MTPA控制策略就是寻找最优转矩角,在单位定子电流工作条件下获得最大转矩。MTPA控制算法可分为两大类[8],一种是利用电机参数计算出最优转矩工作点[9-11],以电磁转矩为输入,利用查表法获得最大转矩电流比转矩角;另一种是不依赖电机参数,通过注入高频电流信号跟踪MTPA曲线。前者系统动态响应快,计算量小,但控制系统需要有足够的存储空间,且一张表只适用一种电机控制。后者对MTPA的跟踪更加精准,但工程计算量大,软件实现复杂。
针对以上问题,本文提出了在传统磁链观测器中加入前馈补偿项的方法,估算转子磁链α,β轴分量,并利用反正切获得精准的转子位置。同时使用新的查表法,实现负载转矩时变下的MTPA控制。新的查表数据与电机参数分离,适用于不同电机,计算量小,可实现快速动态响应。最后在MATLAB/Simulink环境中搭建IPMSM基于该方法的MTPA控制系统的仿真模型,并通过仿真结果验证该方法的优势。
1 磁链观测器转子位置检测
IPMSM在α,β轴坐标系下的电压方程:
(1)
式中:[uαuβ]T,[iαiβ]T分别是α,β轴给定的定子电压和检测到的定子电流;ψf为转子磁链幅值;θe为转子电角度;R为定子电阻,式(1)中的电感满足以下关系式:
(2)
由于IPMSM的Ld≠Lq,所以L1≠0,Lα,Lβ,Lαβ随2θe改变;同时α,β轴坐标系电压和电流存在相间耦合,以上都给转子位置的估算带来复杂性。现将式(2)代入式(1),分离出两倍角项和耦合项,得到电压方程如下:
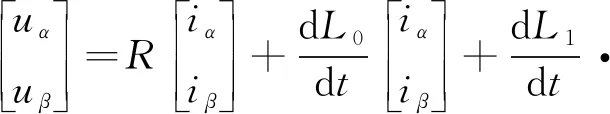
(3)
从式(3)中可以看出,α,β轴的定子电压由四部分组成,即定子电阻压降,固定系数磁链变化率,含耦合项变系数磁链变化率,α,β轴转子磁链变化率。当IPMSM凸极比较大或负载转矩较大时,式(3)等号右边的第一项和第三项均不能忽略。令第三项在α,β轴的磁链分量分别为ψA,ψB,即:
(4)
将式(4)代入式(3)可得:
(5)
(6)
式中:ψfα和ψfβ分别是ψf在α,β轴的分量。
根据Park运算公式:
(7)
对式(4)进行符号变换,得到:
(8)
从式(7)、式(8)可以看出,ψA,ψB可由电流iα,iβ和2θe经过Park运算,再乘以电感L1计算得到。经以上分析,图1给出了转子磁链观测器位置检测框图,通过观测ψfα和ψfβ估算转子电角度θe。
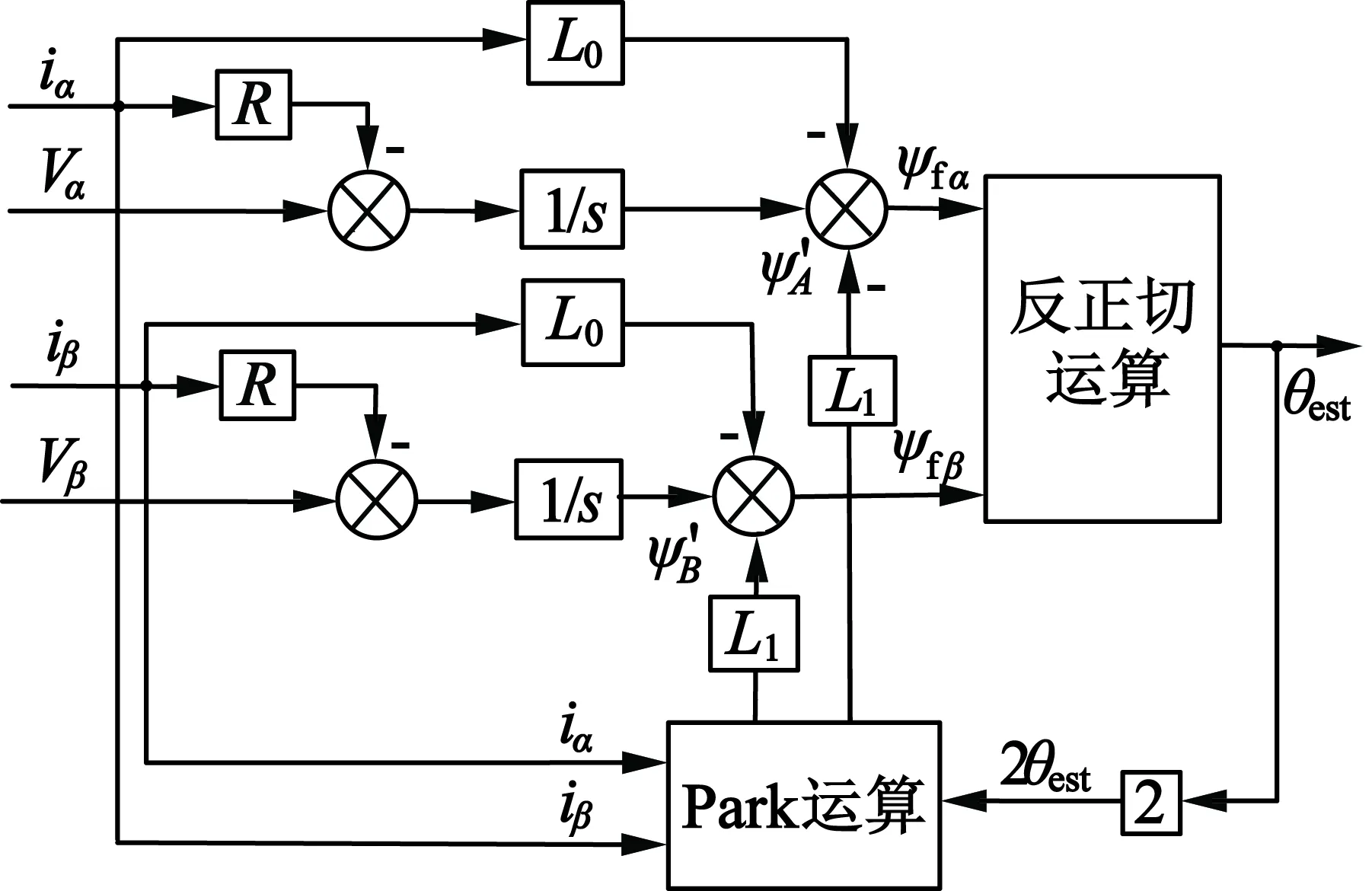
图1 转子磁链观测器框图
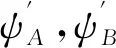
2 MTPA控制
2.1 电磁转矩的组成
旋转坐标系下IPMSM电机的转矩表达式及磁链方程如下:
(9)
(10)
式中:Te为电磁转矩;p为转子极对数;ψd为d轴磁链;ψq为q轴磁链;is为等效定子电流;id为d轴电流;iq为q轴电流;Ld,Lq为分别为d轴和q轴电感;ψs定子磁链;θr为转子位置角度;β为定子电流与d轴的夹角,又称转矩角。
矢量关系如图2所示。
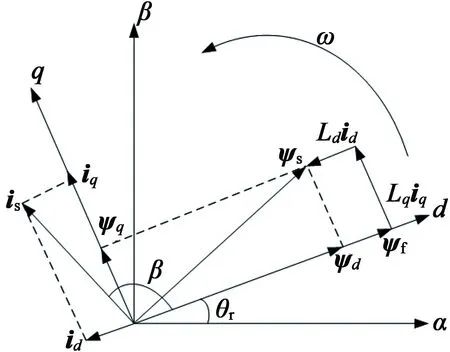
图2 IPMSM矢量图
当定子绕组中通入一组多相对称电流:
(11)
式中:Im为定子电流幅值。在稳态运行时,可得旋转坐标系下d,q轴电流:
(12)
将式(10)、式(12)代入式(9)整理可得:
(13)
Te由两部分组成,即同步转矩Tes和磁阻转矩Ter,表达式分别如下:
(14)
(15)
当β=π/2时,有id=0,iq=Im,则有:
(16)
2.2 最优转矩控制分析
2.2.1 转矩角β与Im的关系
由于Ld
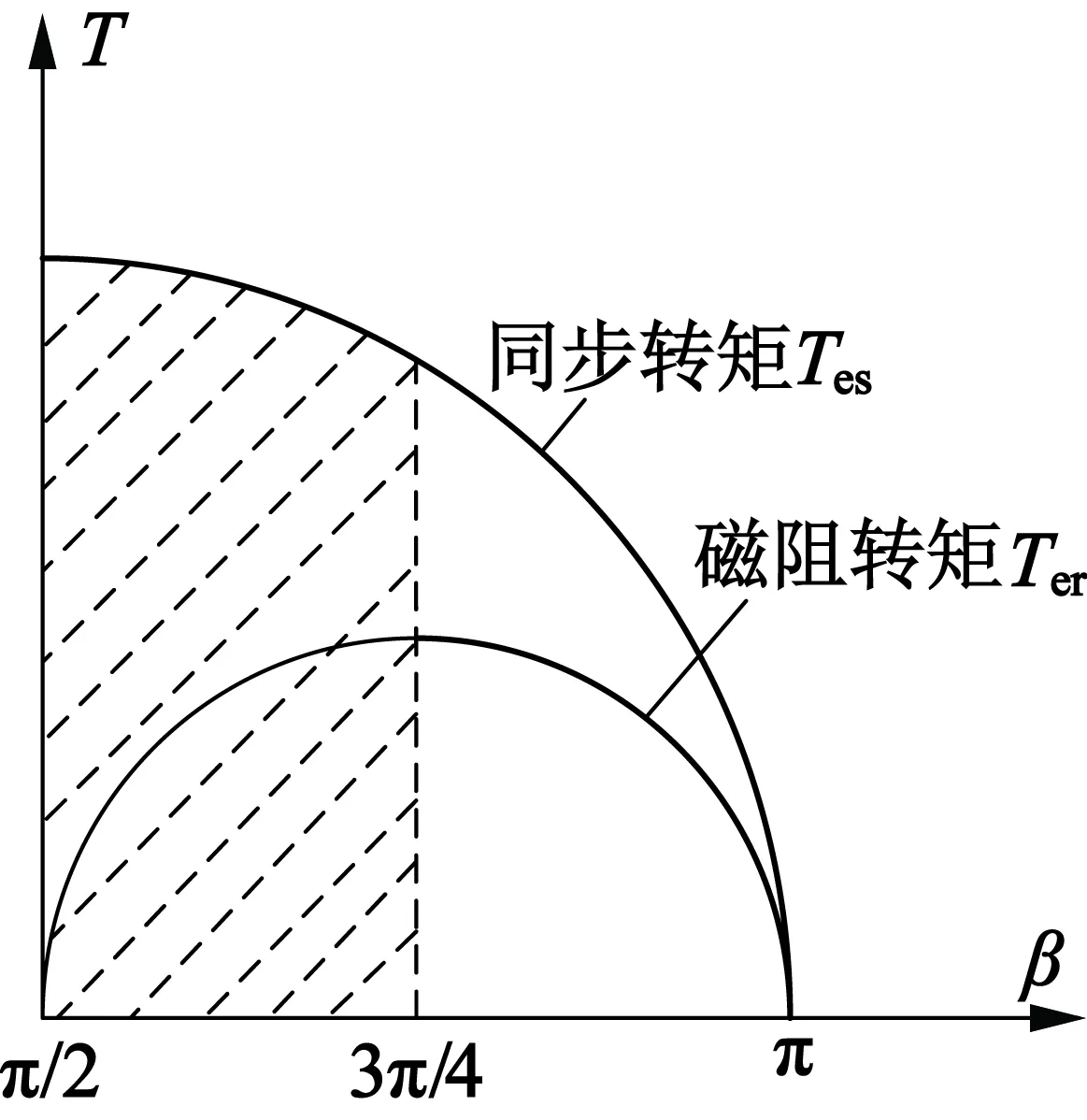
图3 MTPA控制转矩角与转矩关系图
为获得最大转矩电流比,可将式(13)转换如下[12]:
(17)
求上式对β的导数并令其为零,可得:
(18)
令ψfcosβ+(Ld-Lq)Imcos(2β)=0,则:
(19)
根据式(19),求Im对β的导数可得:
(20)
当β在π/2~3π/4范围内时,式(20)大于零,Im随着β单调增;同理β随着Im单调增。
2.2.2 转矩角β与Te的关系
由式(12)和式(19)可得d,q轴电流分量表达式:
(21)
将式(21)代入电磁转矩式(9),有:
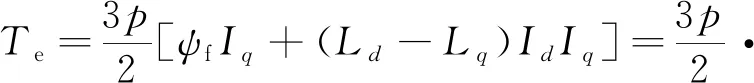
(22)
令:
(23)
则得到电磁转矩Te与β的关系式:
(24)
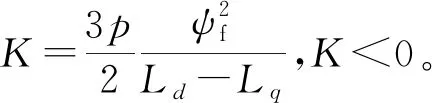
求Te对β导数,可得:
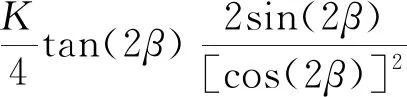
(25)
由于K<0,π/2<β<3π/4,cos(2β)<0,sin(2β)<0,tan(2β)<0,所以式(25)恒大于零,从而可知Te是β单调增函数。当转矩Te确定后,存在唯一的β,使得定子电流最小。
2.2.3 MTPA控制策略
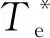

图4 MTPA控制框图
基于以上MTPA控制方式,并结合式(16),图5给出了在相同定子电流Im下,MTPA控制和id=0控制的电磁转矩输出比较。可以看出,随着电流Im越大,电磁转矩Te越大,两种控制方式输出的电磁转矩差值ΔTe越大。目标电磁转矩越大,MTPA控制的优越性越明显。
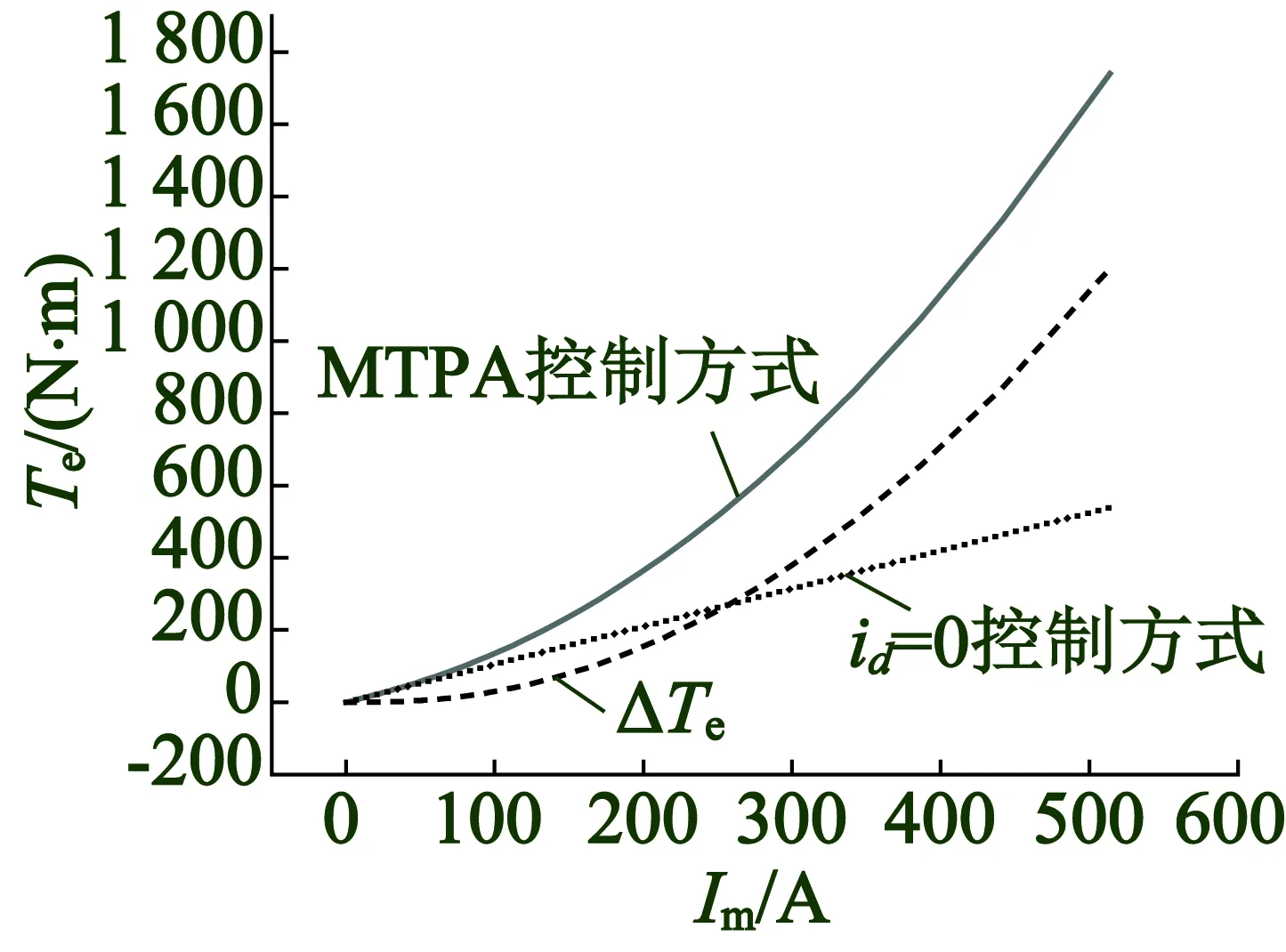
图5 MTPA控制和id=0控制的电磁转矩比较
3 仿真结果及分析
图6给出了MATLAB/Simulink中IPMSM控制系统仿真框图,主要包括电机转速PI控制模块,MTPA控制电流解耦模块,d,q轴电流PI控制模块,SVPWM驱动模块和转子位置估算模块。
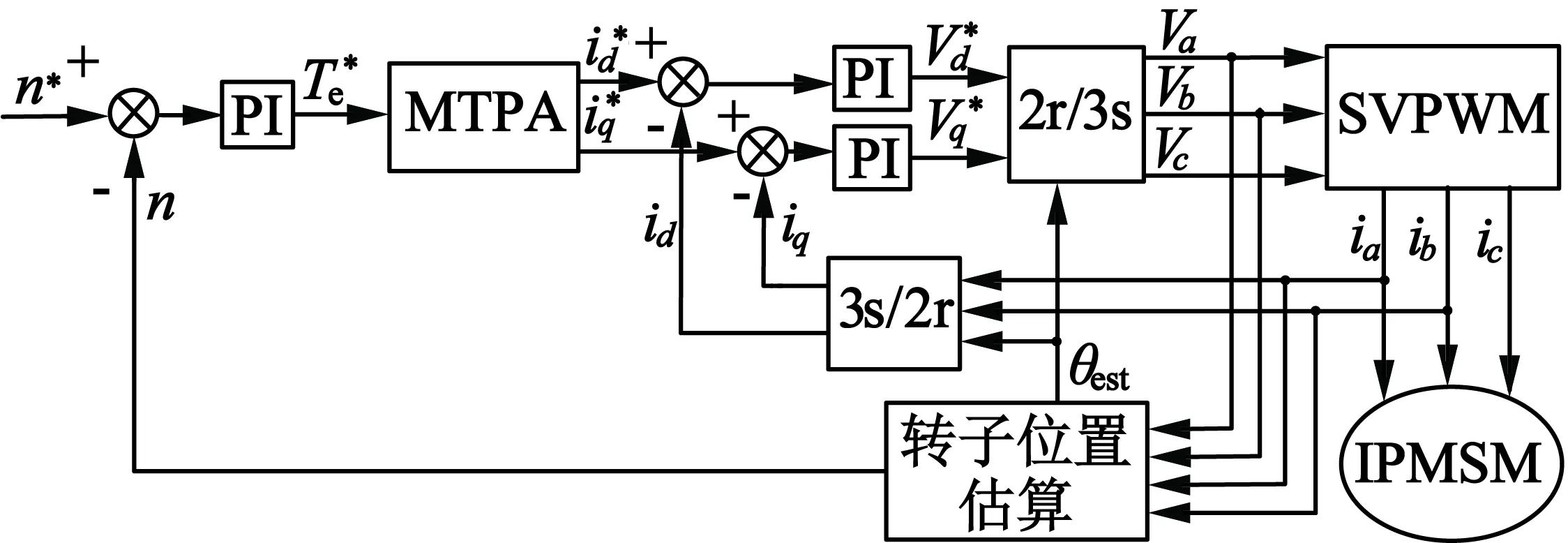
图6 IPMSM控制系统仿真框图
表1给出了IPMSM仿真参数值。

表1 系统仿真参数
仿真中给定的负载转矩如图7所示。给定初始负载转矩为5N·m,随后依次增加到20N·m,40 N·m。
图7 目标负载转矩变化情况
仿真结果如图8和图9所示,给出了在相同负载转矩下,MTPA控制和id=0控制的定子电流输出情况。仿真结果显示,当系统稳定后,在5 N·m和20 N·m处,两种控制方式的输出电流Im相差不明显,但当负载转矩上升到40 N·m时,MTPA控制方式下的Im明显小于id=0控制方式下的Im。
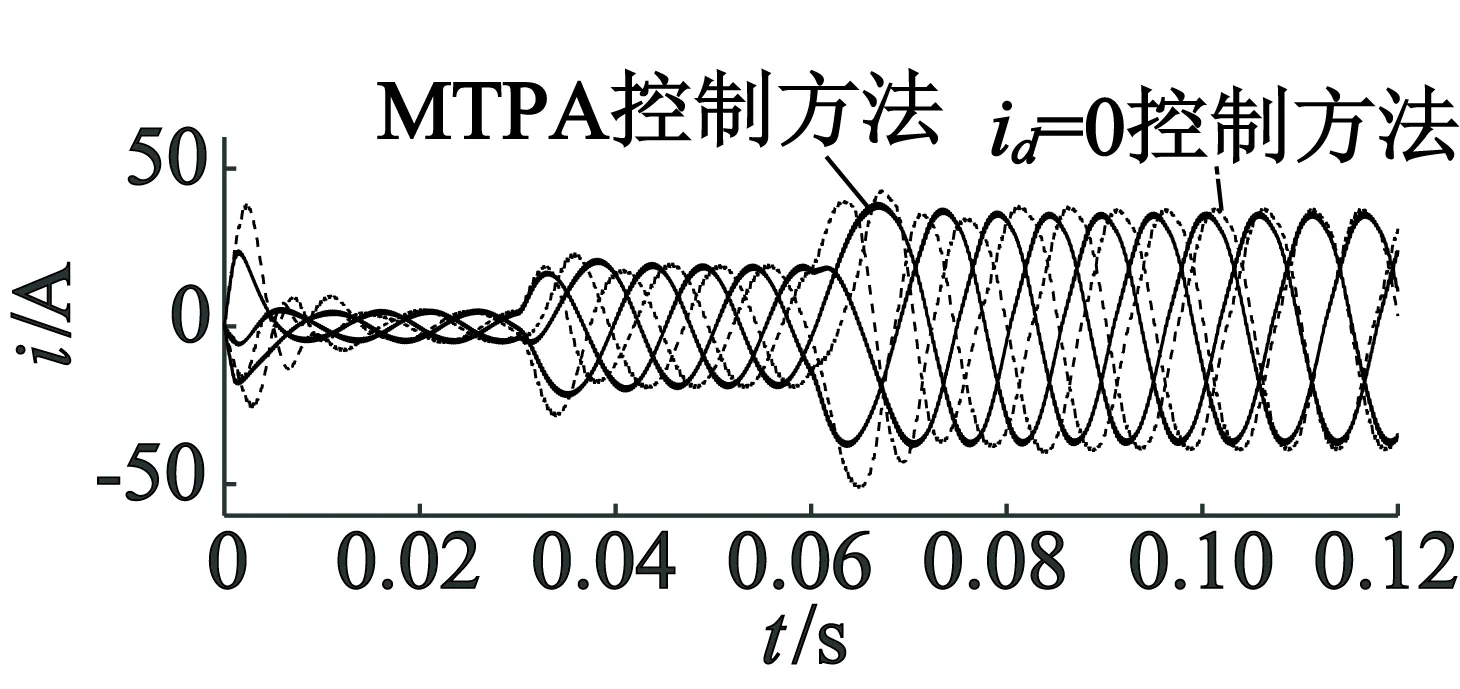
图8 两种控制方式的三相电流波形
图10的仿真结果表明,在MTPA控制方式下,随着负载转矩的增加,iq电流正向增加,id电流反向增加,磁阻转矩Ter的作用越来越明显。
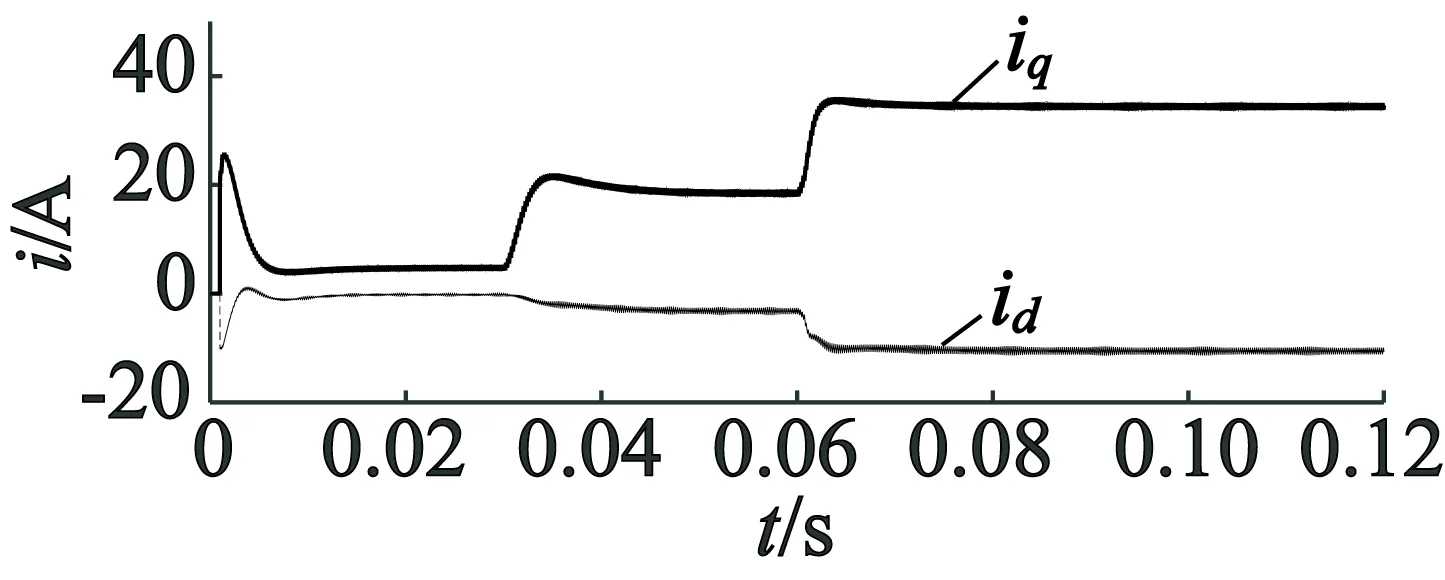
图10 MTPA控制方式下d,q轴电流波形
图11的仿真结果显示,在MTPA控制方式下,转速稳定性好,系统动态响应快,转速波动小。
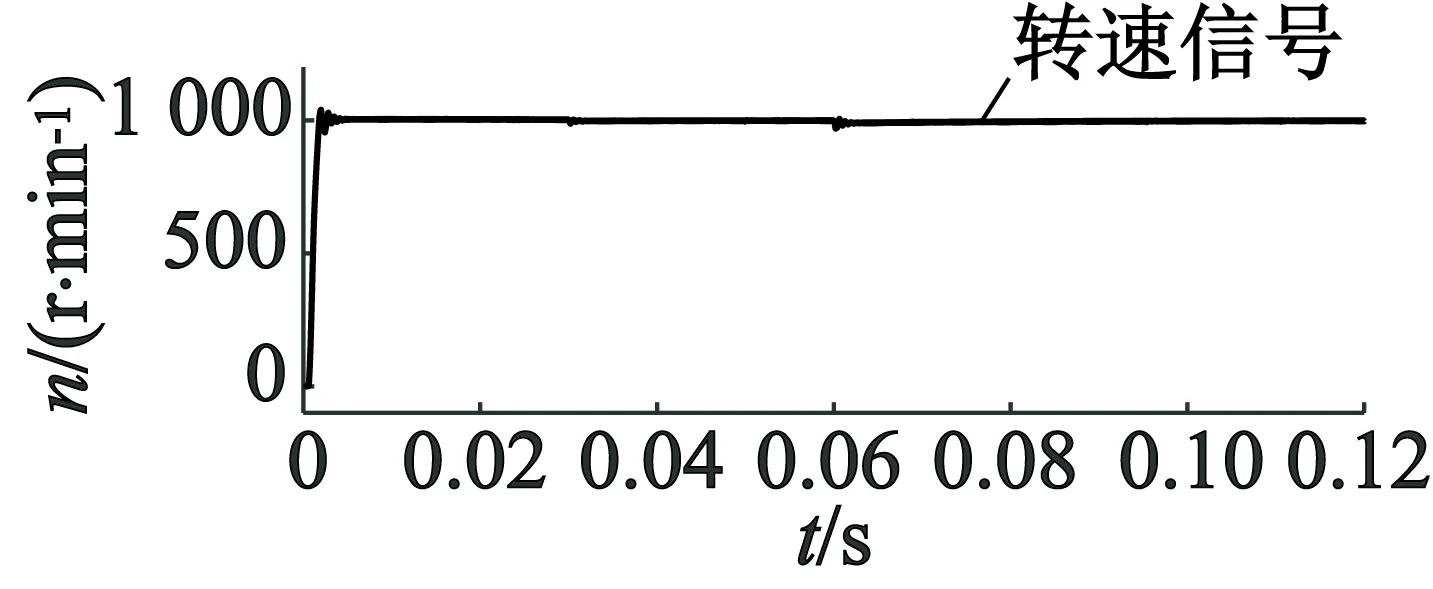
图11 MTPA控制转速信号
图12和图13的仿真结果表明,增加补偿后的转子磁链观测法估算得到的转子位置可以精准地跟踪实际转子位置,并且在负载转矩变化时也可以实现精确的位置跟踪。
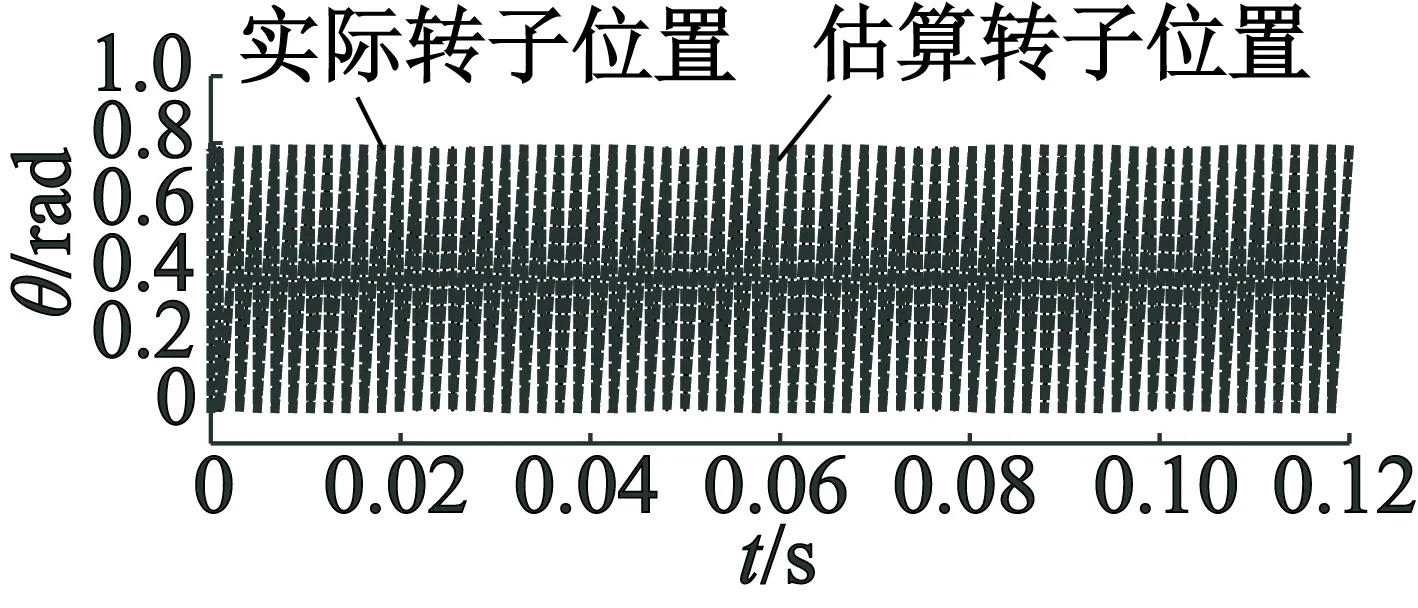
图12 MTPA控制转子位置信号
4 结 语
本文基于IPMSM定子电压方程分析了转子磁链观测器估算转子位置的检测方法,分析了MTPA控制中的转矩角β与电流Im、转矩Te的单调性关系,给出了新的基于查表法的MTPA控制策略,比较了该MTPA控制与id=0控制的转矩输出能力。搭建MATLAB/Simulink系统仿真模型,仿真结果验证了,在相同的负载转矩要求下,新的查表法MTPA控制策略较id=0控制方式输出更小的定子电流,负载转矩越大,MTPA控制方式优越性越明显。该新的查表法将查表数据与电机参数分离,增强了查表数据的通用性,同时实现了在转矩时变系统中对目标转矩的快速跟踪,本研究内容对工程应用场合具有实用价值。
