基于粒子群优化的磁悬浮球系统的模糊强化学习控制

（湖南铁路科技职业技术学院，湖南株洲市，412006） 龚事引

（湖南铁道职业技术学院，湖南株洲市，412006） 李 丹

磁悬浮系统是利用磁场力与物体重力保持平衡原理，而使物体悬浮在某一固定位置。随着智能控制技术的发展，为磁悬浮技术提供了良好的发展前景[1]。

磁悬浮控制系统是非线性迟滞系统，难以建立精确的数学模型。该系统实时性要求很高，传统的PID控制效果并不理想，而模糊控制是不需要掌握受控对象的精确数学模型，鲁棒性较强[2-4]。模糊控制器中量化因子的整定通常难以实现参数最优。强化学习作为一类求解序列决策问题的机器学习方法，是一种求解复杂决策问题的有效手段[5]。粒子群优化可以有效求解大量非线性、不可微和多峰值等复杂问题，被广泛应用到工程技术领域[6]。

本文针对磁悬浮求系统传统PID控制，动态性能较差，控制效果不理想等问题。结合模糊控制、强化学习和粒子群优化算法的优点，提出了一种基于粒子群优化的磁悬浮球系统模糊强化学习控制方法。仿真和实验结果证明，该控制方法的有效性和优越性。

1 磁悬浮球系统模型

1.1 磁悬浮球系统的基本组成

磁悬浮球系统包含光源、电磁铁、传感器、功放模块、控制模块和小球等元件，系统结构如图1所示：

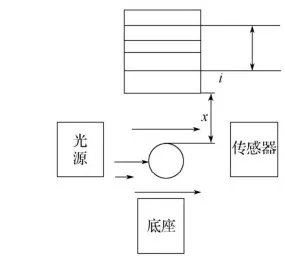
图1 磁悬浮球系统基本结构图

1.2 磁悬浮球系统的数学模型

忽略外界环境的影响，根据动力学原理、电磁理论以及基尔霍夫电压定律，对小球列如下方程：

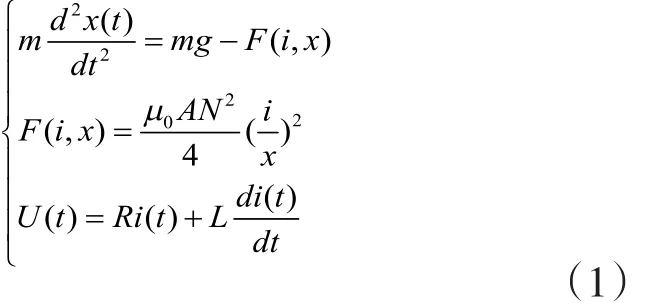
假设小球在平衡时的位移大小为x0，电流大小为i0，则

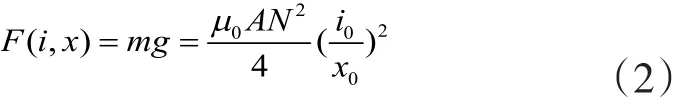
对系统用线性化理论将式（2）进行展开，并将展开式中的高次项舍去，可以表示为：

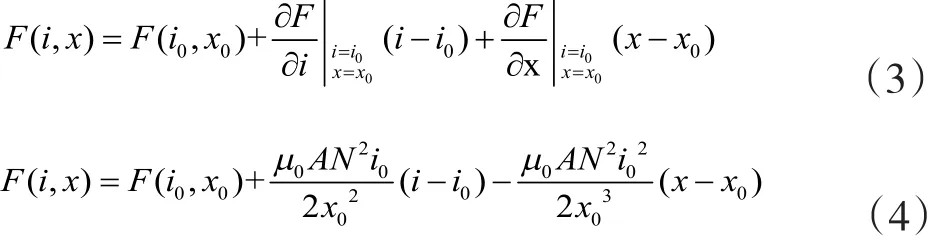
由式（1）和式（4）可得：

2 基于粒子群优化的模糊强化学习控制器设计

本文通过分析磁悬浮球系统的原理和结构，提出一种模糊强化学习控制算法，该算法需要用粒子群算法进行优化，它的结构如图2所示，优点是对系统的参数没有依赖性，一旦选用合适的模糊控制表，系统会呈现较强的鲁棒性。粒子群算法动态优化量化因子ka、kb和比例因子ku可以获得很好的控制效果。

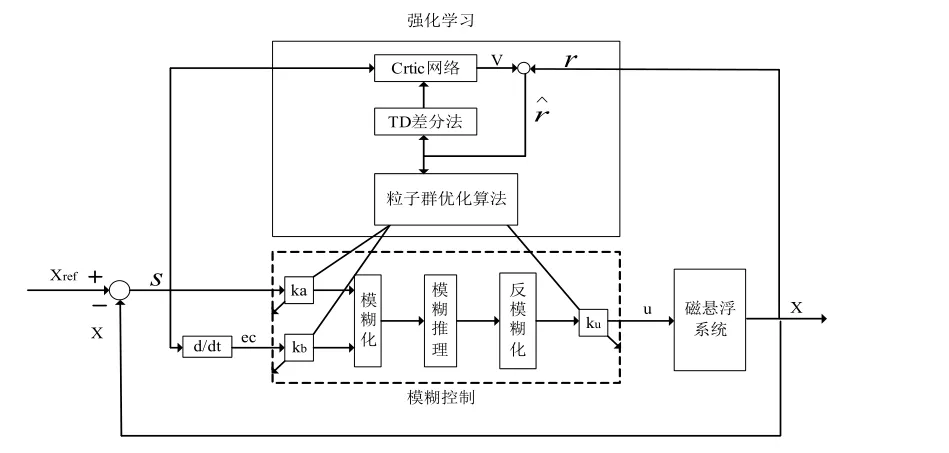
图2 基于粒子群优化的模糊强化学习控制结构

2.1 粒子群优化算法

粒子群优化算法源于对鸟类捕食行为的模拟，是一种新的针对系统全局进行优化的算法，并已在许多领域得到应用。粒子群优化算法一开始需要对一群粒子完成初始化，且这群粒子具有随机性，在不断迭代的过程中找到最优解。在每一次迭代中，粒子通过跟踪个体极值Pbest和全局极值gbest来更新自己。一个是粒子本身所找到的最优解，即个体极值Pbest。当粒子找到个体极值Pbest和全局极值gbest后，就可通过下面2个公式来重新确定自己的速度与位置参数

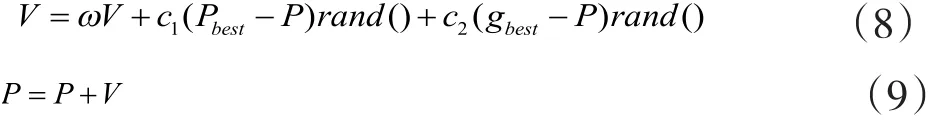
其中：V表示粒子的当前速度；Pr表示粒子的当前位置；rand（）表示随机数，范围可在（0，1）之间；c1和c2表示学习因子，w表示加权系数，范围在0.1～0.9之间。

粒子在不断学习更新的过程中确定最优解的位置，一旦搜索完成，输出的gbest即为全局最优解。在更新过程中，粒子每一维的最大速率为Vmax，粒子的活动范围被限制在允许区域之内。当粒子在全局最优解附近出现“振荡”时，可将最大加权因子wmax减小到最小加权因子wmin。即

其中：k表示当前叠代数；kmax表示迭代总次数。

2.2 基于粒子群优化的Actor网络

粒子群可以用很短的时间和简短的程序来对量化因子ka、kb和比例因子ku三个参数进行优化。具体步骤如下：

（1）首先将所有解分成3个区域，对各个区域的速度和位置qi=[ka，kb，ku]T赋初值，该初值随机产生，此时个体极值pbestt即为初始位置的值；而全局极值gbestt即为各个区域里实现e最小的个体极值，并记录该个体极值的区域号。

（2）将初始位置的值代入公式（8）、（9）中可以求出新的位置和速度，找到新的个体极值，并和全局极值进行比较，若找到的个体极值优于上一次的全局极值，则用找到的个体极值对新的全局极值进行替换。

（3）以此类推，一旦该粒子满足e≤0.001，程序中止，此时粒子所在的位置就是模糊控制器的最优参数（ka、kb和ku）。否则，继续寻找。

3 系统建模仿真及结果分析

根据以上分析，本文基于Matlab中的Simulink环境下建立基于粒子群优化的磁悬浮球系统模糊控制的仿真如图3所示。

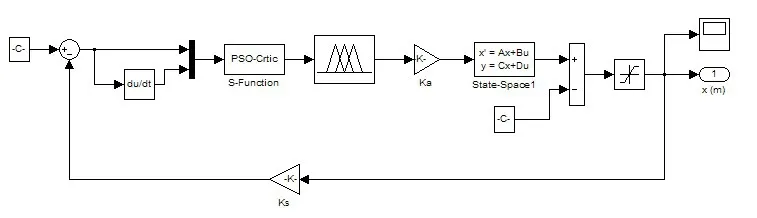
图3 基于粒子群优化的磁悬浮球系统模糊强化学习控制仿真

磁悬浮控制系统的仿真研究采用一组实际工程数据：小球质量m=460g，线圈等效电阻R=9.6 Ω，线圈等效电感L=109mH，x为气隙间距，F为电磁力，A为铁芯面积，空气磁导率u0=4×10-7H/m。

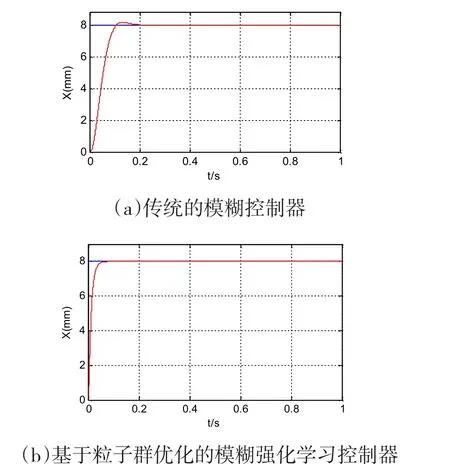
图4 基于粒子群优化的模糊强化学习控制仿真波形

从图4可知，与传统的模糊控制相比基于粒子群优化的模糊强化学习控制器的磁悬浮求系统的响应速度快，稳态误差小，系统跟随性较好，证明了该控制算法的有效性和优越性。

4 结论

本文在搭建状态空间模型后，采用粒子群优化算法对模糊强化学习控制器的参数进行了优化，并在MATLAB中进行了仿真。通过仿真对比试验，结果表明，用粒子群算法优化后的模糊强化学习控制器能使系统快速稳定达到预期，并能有效抑制磁悬浮球系统抖动。