大型风力发电机组控制技术研究
2021-02-28张美伦朱明泽赵剑锋
张美伦,朱明泽,张 瑾,赵剑锋,张 睿
(1.国网黑龙江省电力有限公司电力科学研究院,哈尔滨 150030; 2.哈尔滨电气国际工程有限责任公司,哈尔滨 150028;3.国网黑龙江省电力有限公司,哈尔滨150090; 4.大连土城子风电有限公司,辽宁 瓦房店116327;)
0 引 言
随着风电机组单机容量与风电规模的不断提高,风电渗透率逐渐增高,现代风电机组的运行控制不但注意到风电场正常状态下的遥测、监控,而且开始转向风电机组与电网系统相互协调一体化的运行控制研究[1],如风电机组有功功率控制、无功功率控制、低电压穿越以及对称和不对称故障下的安全运行(故障穿越)问题等。因此,根据调度指令进行单机有功、无功调节,实现大型风电机组的自适应调节与并网,从电网层面灵活响应对风电机群有功、无功控制和优化调度的要求具有重大意义。
目前,国内对大型风力发电控制技术的研究只停留在传统控制技术上面,这种方法采用了线性控制方法,是以线性模型为基础,但是对于急剧变化的风速调整具有相对滞后的缺点[2]。此外,采用基于某一工作点的线性模型方法只能够保证在线性化工作点附近的控制效果,因此并不适用于运行范围广、不确定性强、随机扰动大、具有严重非线性特征的风力发电系统[3]。
针对上述问题,提出将现代控制方法(包括人工智能控制、最优控制、自适应控制、鲁棒控制、切换控制等)引入大型风电机组的控制中,对大型风力发电机组的动态进行建模,研究风电系统的控制方式和设计有效的控制律,使风力发电机组对参数摄动和负荷扰动具有强鲁棒性,保证风电机组安全高效运行。
1 系统关键控制技术研究
采用快速最佳叶尖速比控制实现柔性变桨,在最佳叶尖速比控制的基础上,引入自适应分段控制技术,设计大型风电机组的智能化柔性变桨算法和柔性偏航算法,实现大型风电机组有功、无功的分段线性控制。具体通过以下各个小节描述的优化控制技术,保证了系统实现柔性变桨、变速与偏航,以及风电机组的整体智能化控制,降低对整机各个部分的冲击,实现低噪声运行。
1.1 最佳叶尖速比控制
叶尖速比是叶片叶尖线速度与风速的比值[4],最佳叶尖速比法是在不同风速下,通过机械侧转换器控制电动机的转子速度,使得风力涡轮机可以在最佳叶尖速比的状态下运行,由此获得风电功率最大值[5]。最佳叶尖速比控制方法的原理如图1所示。根据当前测得的风速v,经查表可知该风速下的最佳叶尖速比,并将该值作为参考值λref。测量当前叶片转速ω,通过公式λ=ωR/v计算获得叶尖速比,与参考值进行比较后,进行PI调整,将调节器输出信号发送至风机控制系统,由此可实现风机最佳叶尖速比控制。

图1 叶尖速比控制图Fig.1 Diagram of tip speed ratio control
1.2 完全独立变桨控制
完全独立变桨控制的目标是实现全扫风面变桨,减少叶片应力周期性冲击,稳定整机载荷和延长叶片寿命。在实现完全独立变桨控制的基础上,才能够实现单个叶片的自适应控制[6]。
独立变桨距控制系统如图2所示,独立变桨控制器的功能主要是控制系统的位置、转矩、速度等参数,独立变桨伺服驱动器具有定位和同步调整的功能,桨距角位置经内齿传感器检测,与伺服电机的转子位置进行同步,桨距角可以用作反馈状态变量,以实现伺服电机的同步控制,由此达到独立变桨控制。

图2 独立变桨距控制系统图Fig.2 Diagram of independent pitch control system
1.3 叶片自适应控制
大型风电机组是一个复杂的非线性系统,难以获得系统的所有控制状态,但控制系统的输入和输出量是确定的,因此可根据被控对象的状态空间建立模型参考自适应控制系统[6]。
建立3个叶片运行一周的状态空间模型,将3个叶片的控制目标设计为同一个参考模型,利用李雅普诺夫函数直接法设计3个叶片的模型参考自适应控制率,使得3个叶片在运行一周的过程中对主轴的应力尽量保持一致,变桨系统对于塔筒效应和叶片制造过程中的离散性误差有着明显的适应性,控制性能良好,能够有效保证系统的稳定性。
完全独立变桨控制与叶片的自适应控制相结合,实现了风机的自适应分段控制,在低风速(启动风速至5 m风速)、中段风速(5 m至额定风速)、高风速(额定风速以上)时,分别设置了3个不同的参考模型,使得系统在这3段风速之下可以很好地实现最大功率跟踪控制的同时,3个叶片保持平衡,对主轴冲击最小,具体结构图如图3所示。
1.4 柔性偏航
偏航控制的主要功能之一是能够使风轮跟踪变化稳定的风向,通过控制风轮的迎风面与风向始终保持垂直以实现风能的最大捕获[7]。当风向发生变化时,由风速风向仪测得风向变化,由偏航控制器控制偏航驱动装置中的3~5台偏航电机旋转,偏航电机通过减速齿轮箱带动小齿轮旋转,使机舱往风速变化的方向同步运转。
原有的偏航电机(3~5台)在运行过程中出现不能完全同步现象,即偏航过程中某个偏航电机驱动的小齿轮与另一个偏航电机驱动的小齿轮无法完全同步带动大齿圈,导致互相拉扯发出低频噪音的现象。为此,采用主从力矩变频驱动偏航策略,使得多个偏航电机能够完全同步运行。采用主从力矩变频驱动的柔性偏航技术,除了降低噪音外,还能够延长齿圈和电机的使用寿命。
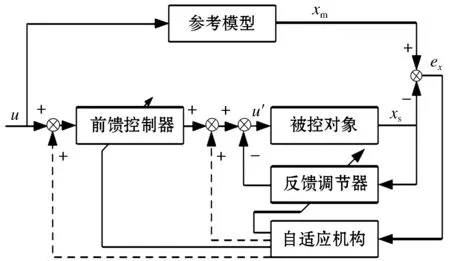
图3 独立变桨线性时变参数系统自适应控制结构图Fig.3 Adaptive control structure diagram of independent pitch linear time-varying parameter system
1.5 低电压穿越
当电网电压下降时,电网侧变流器会出现过流现象,如果采取限制电流的措施,直流母线就会产生过电压;如果没有采取有效的保护措施,将无法保证风机的安全稳定运行[8]。因此,需根据实际的风电状态、持续时间、电压跌落等情况,确定机组采用的保护策略,以满足风电并网时的低压穿越要求。
在风速低、系统压降小的情况下,适当提高系统侧变流器电源装置的过电流水平和直流侧电容器的抗电压水平,可以实现低电压穿越。但如果风机在额定状态下运行时,电网电压大幅下降,且持续时间较长, 变流器的成本会大幅增加, 因此这种保护措施并不适用。
在风速高且电网电压大幅下降的情况下,在发电机直流侧和输出端增设Crowbar电路或辅助变流装置,主要作用是限制故障时转子侧的过电流和过电压,可以消耗、转移或存储过剩的能量,使得风机在电网发生故障时也能够实现低电压穿越,过程如图4所示。
在图4中保护点1位置增加Crowbar电路,在电网电压跌落的情况下,该电路能够平衡输入与输出间的能量差,避免了变流器过电流和直流母线过电压对风机产生的冲击。当电网电压恢复正常时,则迅速切断Crowbar电路,使风机恢复正常发电状态运转。
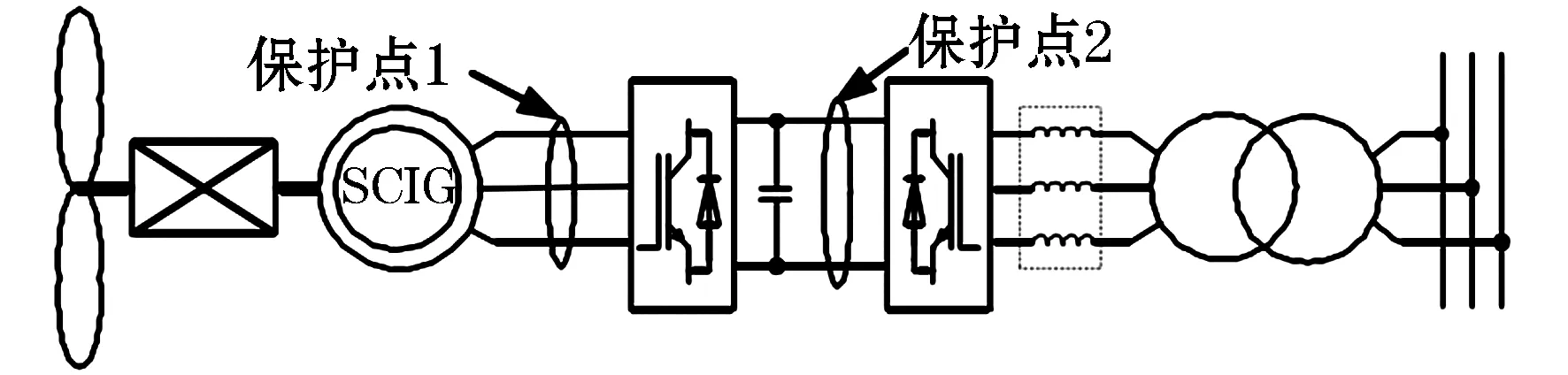
图4 电机直流侧和输出端增设Crowbar电路Fig.4 Crowbar circuit is added to the motor output terminal and DC terminal
2 控制策略研究
结合传统矢量控制的基本思想,引入自抗扰控制(adaptive disturbance rejection control,ADRC)、神经网络,设计一种抗干扰能力较强控制算法,控制器内环基于BP神经网络实现转子d、q轴电流控制,控制器外环基于自抗扰控制的有功、无功控制,目标是使得控制系统对内、外扰动具有较强的鲁棒性。根据传统控制模式的不足,结合自抗扰控制的优点和BP神经网络的优点,采用基于神经网络的电流内环控制和基于自抗扰控制的功率外环控制。系统整体的控制拓扑图如图5所示。
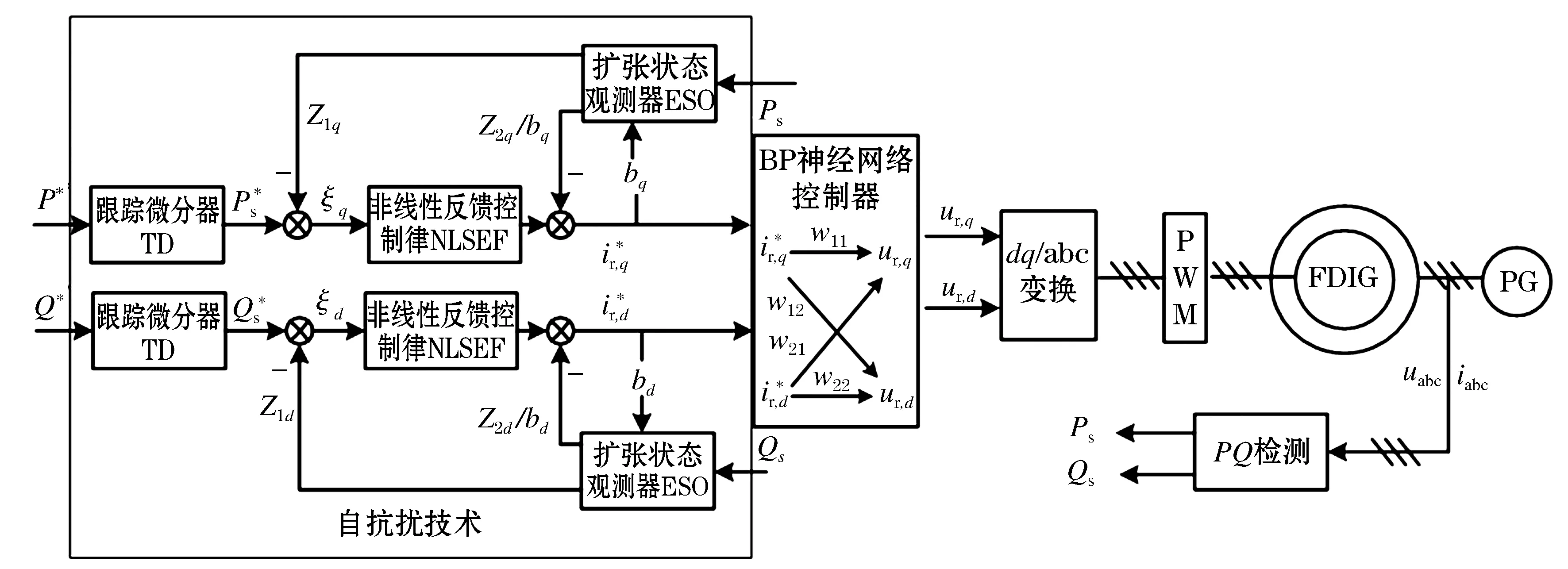
图5 基于自抗扰神经网络控制技术原理图Fig.5 Schematic diagram of control technology based on adaptive disturbance rejection and neural network
2.1 自抗扰控制系统设计
自抗扰控制系统的设计包括三个部分:跟踪微分器TD(tracking-differentiator)、扩张状态观测器ESO(extended state observer)和非线性反馈控制律NLSEF(nonlinear states error feedback)。各个部分相关的参数采用“分离性原理”独自整定。
1)跟踪微分器TD设计
对有功功率和无功功率的跟踪采用一阶微分器。微分器的模型如下:
(1)
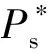
(2)
2)扩张状态观测器ESO设计
以检测的双馈电机定子侧有功功率Ps和无功功率Qs为量测输入分别构造扩张状态观测器,如式(3)所示。
(3)
式中:x代表d或q;y表示P或Q(当x为d时,y为Q;当x为q时,y为P);Z1x为定子有功功率和无功功率的实际跟踪值;Z2x为扰动量的估计值;仿真时具体的相关参数取值β1x为300,β2x为400,α1x为0.8,δ为0.005,bx为500。
3)非线性反馈控制律NLSEF的设计

(4)
式中:βq的值为400;βd的值为350;αq和αd都为0.7;δ为0.005。
2.2 BP神经网络控制系统设计
BP神经网络控制器通过在线调节权值w11、w12、w21、w22使有功功率和无功功率的目标函数逐渐达到最小值,从而实现发电机有功功率和无功功率的独立跟踪控制,BP神经网络的目标函数为
(5)
根据梯度法调节权值,得到权值变换量,具体如下:
(6)
式中:η为学习速率,取值为0.1。由式(6)可以对权值不断更新,从而搜寻到一组最优权值使目标函数为最小值。
3 仿真结果与分析
为了验证ADRC-BP控制技术的性能,在Matlab 2012b/Simulink平台上对双馈发电机分别采用空间矢量控制方法和基于ADRC-BP控制方法进行仿真。仿真所用双馈电机的主要参数为:定子额定电压690 V,额定功率2.0 MW,定子电阻为3.74 Ω,定子漏感为0.31 H,转子电阻为3.2 Ω,转子漏感0.31 H,定转子互感1.2 H,极对数为2。系统额定风速为11 m/s,输入风机的风速为9 m/s(此时对应的视在功率为1 MW)。
仿真验证包括三个部分:当电网对称,给定功率发生变化时,比较两种控制算法的性能;当双馈电机参数发生变化,给定功率不变,比较两种控制算法的性能;当电网电压出现波动,给定功率不变时,比较两种控制算法的性能。
1)当有功功率和无功功率参考值变化时
保持输入风速不变,并设定有功功率参考值为600 kW,无功功率的参考值为800 kvar;在仿真时间为0.5 s时,将有功功率和无功功率的值分别设定为800 kW、600 kvar,采用空间矢量控制算法和ADRC-BP算法得到的仿真结果如图6所示。
2)当电机参数发生改变时
保持输入风速不变,并设定有功功率参考值为800 kW,无功功率的参考值为600 kvar;在仿真时间为0.5 s时,双馈电机的定子侧电阻变为原来的1.5倍,采用空间矢量控制算法和ADRC-BP算法得到的仿真结果如图7所示。
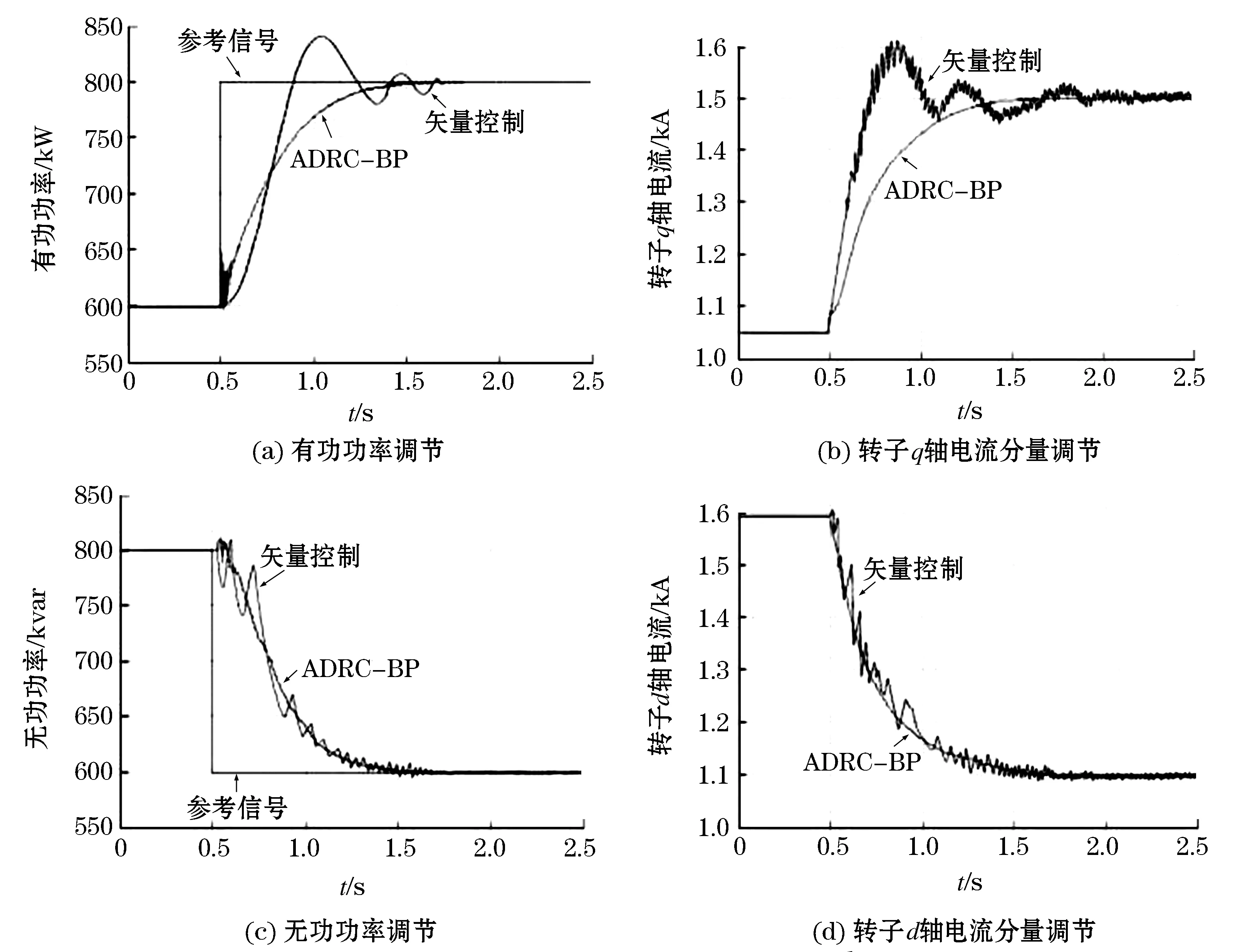
图6 功率参考值变化时电气量仿真波形对比图Fig.6 Comparison diagram of electrical quantity simulation waveform when power reference value change

图7 电机参数变化时电气量仿真波形对比图Fig.7 Comparison diagram of electrical quantity simulation waveform when motor parameters change
3)当电网电压波动时
保持输入风速为9 m/s不变,并设定有功功率参考值为800 kW,无功功率的参考值为600 kvar;在仿真时间为0.5 s时,电网电压变为原来的0.9倍,且在1s时变为原来值,采用空间矢量控制算法和ADRC-BP算法得到的仿真结果如图8所示。
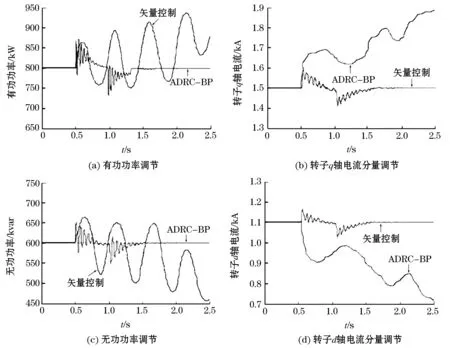
图8 电网电压波动时电气量仿真波形对比图Fig.8 Comparison diagram of electrical quantity simulation waveform when grid voltage fluctuates
如图6~8所示,当参考功率变化时,ADRC-BP算法比矢量控制算法具有更快的跟踪速度,且波动量小;当电机参数改变时,ADRC-BP算法经过短时间平缓地过渡到稳态,且稳态无误差,而矢量控制的波动性比较大,且达到稳态所需时间较长;当电网电压波动时,ADRC-BP算法能够经过调整最终达到稳态,而矢量控制最终导致发散。由此可知,当电网处于不同运行状态时,采用ADRC-BP控制方法提升了系统的稳定精度,使系统具有较好的稳态性能和较强的鲁棒性。
4 结 语
该文结合风电机群能量管理与优化调度对大型风电机组的技术需求,在模型仿真和控制策略验证的基础上,引入自适应分段控制技术,并设计了自抗扰控制系统,设计了智能化柔性变桨算法和柔性偏航算法,实现了风电机组有功无功的分段线性控制,并具备低电压穿越能力,降低机组运行噪声,延长机组寿命,提升了大型风电机组的自适应控制能力。
