一种利用对抗性学习提高推荐鲁棒性的算法
2021-02-28吴哲夫李泽农吕跃华龚树凤
吴哲夫,李泽农,吕跃华,龚树凤
1(浙江工业大学 信息工程学院,杭州 310023) 2(浙江省科技信息研究院 信息技术中心,杭州 310006)
1 引 言
随着互联网技术的飞速发展,互联网用户的数量得到了快速增长,互联网产品的需求也大大提高.电子商务、社交网站、在线阅读等与生活有着密切关系的互联网产品都在互联网环境下蓬勃发展,人们的生活也因此变得越来越便利.但与此同时,在这些呈现出爆炸式增长的信息量中,人们不得不花费大量的时间与精力来获取对自己有价值的信息.在这个“信息过载”的时代,传统的搜索引擎技术已无法满足针对不同的用户来提供不同的个性化服务需求.因此,推荐系统[1]应运而生,它通过分析用户的历史活动行为,挖掘出用户的潜在偏好,从而向用户推荐其可能感兴趣的物品,满足用户的个性化需求[2].个性化推荐技术得以广泛应用,典型应用包括国外电子商务领域的Amazon,社交领域的Facebook、Twitter,新闻推荐领域的Google News等.这些应用和平台通过推荐系统,很好地解决了用户个性化需求的问题,并且获得了可观的商业价值和经济效益[3].
近年来,有研究发现深度神经网络能够对正确输入的图像进行分类.但是,对这些图像添加微小扰动后,神经网络可能会导致完全错误的分类结果,即这些微小扰动使得预测误差扩大化.为了解决这类问题,研究人员提出了一种对抗性学习方法,即在训练过程中动态性地生成对抗性样本.除了将微扰加载在神经网络输入层,研究人员还尝试了在嵌入层和dropout层进行添加.受此启发,对抗性学习方法同样适用于推荐系统领域,通过使用对抗性学习方法能够增加模型抵御来自外界恶意攻击的能力,从而提升模型的鲁棒性.
本文提出了一种基于对抗性学习提高推荐鲁棒性的算法,通过使用对抗性学习训练方法不仅提高了模型的推荐性能也增强了模型的鲁棒性.首先研究了美学因子作为新的视觉特征对推荐模型鲁棒性的影响;然后添加对抗性扰动提出了一个ADCFA(Adversarial Dynamic Collaborative Filtering Model with Aesthetic Feature)算法,并通过使用对抗性学习训练来提高推荐模型的鲁棒性;并且提出了一种改进的ADCFA-SGD学习算法进行模型参数求解;最后,将所提对抗性学习算法应用于Amazon数据集验证了其有效性.
2 相关工作
在过去几十年,学者们提出了各种推荐算法并且已经被广泛地应用到各类推荐系统中.在当前的推荐系统算法研究中,绝大多数都是集中在提高推荐的准确率上,例如Du 等人将视频中所包含的文本信息、音频信息、图片中的语义信息和美学特征等分别或同时纳入推荐模型以改善对于视频推荐的准确度[4-7];He 等人融合时间因子、社会关系和视觉特征于一体对艺术品做推荐[8].还有使用新的融合方法[9-10]或新的特征提取技术[11]来优化算法,例如通过将多特征空间映射到一个统一空间实现融合的;或者使用不同特征的结果列表,利用其候选结果来进行融合实现.
但这些研究都专注于推荐的准确率而忽略了其鲁棒性的问题.Goodfellow在其关于对抗性实例[12]的研究中指出:当一张图片受到外界的扰动干扰时,图片分类器得到的结果会存在一定程度的偏差[13,14].对于推荐算法来说,类似的现象同样存在.到目前为止,推荐系统领域对于鲁棒性研究[15,16]还不多,仅包括了用户、产品对于推荐算法鲁棒性的影响和 CNN 视觉特征对于推荐算法鲁棒性影响等方面的研究.
视觉特征是影响推荐模型的一个重要的影响因子.近期,有研究表明利用新的网络结构 BDN(Brain-inspired Deep Network)提取的美学因子相较于从传统卷积神经网络提取的CNN特征,对于推荐系统能起到更好的推荐效果.为了探究美学因子作为视觉特征对模型鲁棒性的影响,本文选择了DCFA模型[17]作为基础模型来展开研究,并提出了一种基于对抗性学习提高推荐鲁棒性的算法.
3 准备工作
本节主要介绍了用于提高鲁棒性的基础模型DCFA以及研究了该模型的脆弱性,首先讨论了在模型中添加扰动的位置,然后通过在DCFA模型中分别加入随机扰动和对抗性扰动来比较模型性能的变化,以此来验证改善此模型鲁棒性的可行性.
3.1 DCFA模型
DCFA模型结合了用户历史消费行为和产品的视觉特征,能够捕捉不同用户随着时间变化而变化的审美偏好,因而能给用户在不同的时间推荐适合的产品.
DCFA模型相较于仅仅利用从传统的卷积神经网络提取的CNN特征作为视觉特征外,还加入了美学特征,它将从产品图片中提取出的CNN特征和美学特征结合起来作为视觉特征融入到张量分解模型中,为避免CP(CANDECOMP/PARAFAC)[18]和Tucker[19]分解存在的诸如稀疏数据收敛性差、对于大规模数据集的扩展性差等不足之处,选择CMTF(Coupled Matrix and Tensor Factorization)[20]框架来进行张量分解,其预测模型为:
(1)
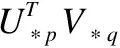
DCFA模型使用典型的贝叶斯个性化排序[21]优化标准对用户的隐式反馈(购买记录)进行优化.构成的目标函数为:
(2)

(3)
(4)
(5)
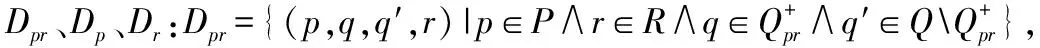
3.2 DCFA模型的脆弱性
扰动通常被加入到模型输入或模型参数中,本文研究的是美学特征在加入扰动后的影响.由于美学特征是从图片中提取的,理论上将扰动加入到上述两个位置都可行,但将扰动加入到模型输入中却会遇到一些实际问题:
首先如果选择在模型输入处加入扰动,由于系统从图片输入开始,在训练算法模型的时候对用于提取两个视觉特征网络的参数会持续更新,并且模型输入的原始用户信息和产品的交互信息往往是稀疏的,而提取视觉特征的网络有很多参数,同步训练容易引起过拟合问题.
其次在模型输入处添加扰动会导致模型训练的复杂度大大增加.假如本文给模型输入一个实例,不仅需要更新算法模型所涉及的用户、产品、时间等矩阵,同样梯度变化的数据也需要回传到提取视觉特征的网络,以此对整个网络进行更新,而神经网络的参数往往都比模型参数大很多倍,这就势必使得训练过程更加耗时,增加了复杂度.
为了避免产生这些问题,本文选择在模型参数中加入扰动,一方面能避免提取图片特征的网络与模型训练过程产生交叉影响,另一方面也能提升算法的效率.
DCFA模型将从图片中提取的CNN特征和美学特征整合的嵌入式矩阵作为模型参数来预测用户的偏好.根据上节的讨论,本文选择在该模型参数中分别加入随机扰动和对抗性扰动,通过调整超参数ε的大小来控制扰动幅度的大小,以此来对比模型在这两种情况下性能的变化.本文选用亚马逊数据集计算,并使用F1@10和Recall@5两个指标来衡量模型性能的好坏.实验结果如图1所示.

图1 在不同噪声类型下的性能对比
从图1可以观察到当该模型加入随机扰动(DCFA-rand)时,模型性能的变化较小;而当加入对抗性扰动(DCFA-grad)后,模型性能整体呈下降趋势,并且当扰动变大时,性能明显下降.该结果表明DCFA模型易受到对抗性扰动的影响,因此可以通过对抗性学习来改善模型的鲁棒性.
4 提高推荐鲁棒性的算法
本节将详细介绍在DCFA模型上添加对抗性学习来改善鲁棒性的新模型ADCFA的组成和训练方法.
4.1 ADCFA预测模型
根据上节知,DCFA模型易受到对抗性扰动的影响,在DCFA模型的基础上添加对抗性扰动得到了一个ADCFA的预测模型,其定义为:
(6)
其中,Δ*∈RK表示加入到视觉特征矩阵的对抗性扰动.类似于DCFA,本文使用BPR来优化训练模型参数.该预测模型示意图如图2所示.
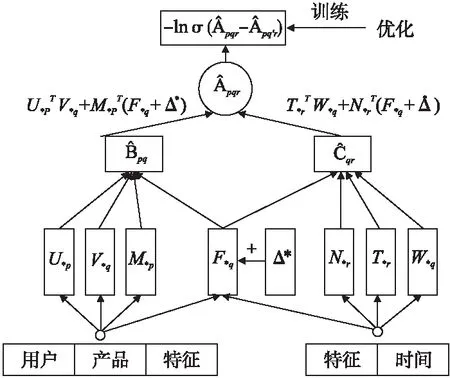
图2 ADCFA模型框架图
4.2 对抗性扰动的构建
DCFA是一种用BPR优化的时间感知美学推荐模型.本文使用SGD(Stochastic Gradient Descent)训练DCFA模型,直至模型达到收敛,目的是找出最坏情况的扰动,这将导致对模型的影响最大;另一方面,由于DCFA模型经过训练以最小化BPR损失,因此将BPR损失最大化作为相反的目标,以获得对训练数据的最佳扰动,即添加在模型参数处的对抗性扰动:
(7)
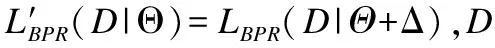
(8)

(9)
(10)
(11)
4.3 模型优化
为了获得对对抗性扰动不太敏感的模型,除了最小化原始BPR损失之外,还需最小化被扰动模型的目标函数并将模型的优化目标定义为:
(12)
其中,Θ为模型参数,包括用户、产品以及时间的嵌入矩阵U、V、T,用户偏好矩阵M,产品潜在特征矩阵W,时间r的偏好矩阵N,特征矩阵F;λ是控制被扰动模型的目标函数对模型优化影响的一个超参数,当λ设置为0时表示模型没有加入任何扰动.
总的来说,ADCFA模型的训练就像进行一场极大极小值的游戏:
(13)
本文把模型参数Θ和扰动Δ看成玩这场极大极小值游戏的两个玩家,类似博弈论中的二人零和博弈[22],即二人的利益之和为零,一方所得正好是一方所失.从模型参数Θ的角度出发,为了赢得这场游戏,它肯定希望最小化自己的损失而最大化对手的损失,反之亦然.
4.4 学习算法
在BPR损失中由于存在大量成对训练实例,使用批量梯度下降方法非常耗时并且收敛速度慢,为此本文考虑基于SGD算法[23]为ADCFA设计了参数学习算法.
算法:ADCFA-SGD学习算法.
输入:训练集D,学习率η,控制对抗性扰动幅度的超参数,
对抗性正则化超参数λ,正则化系数λθ,迭代次数iter_max;
输出:模型参数Θ.
1.训练DCFA得到收敛参数初始化Θ;
2.初始化循环次数iter=0;
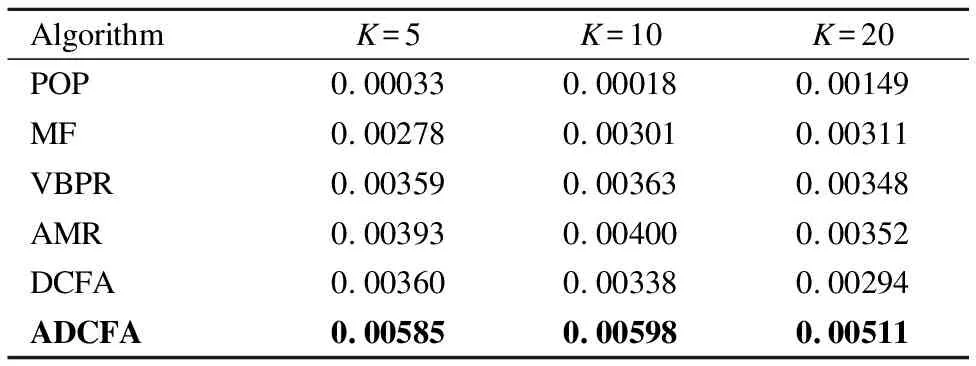
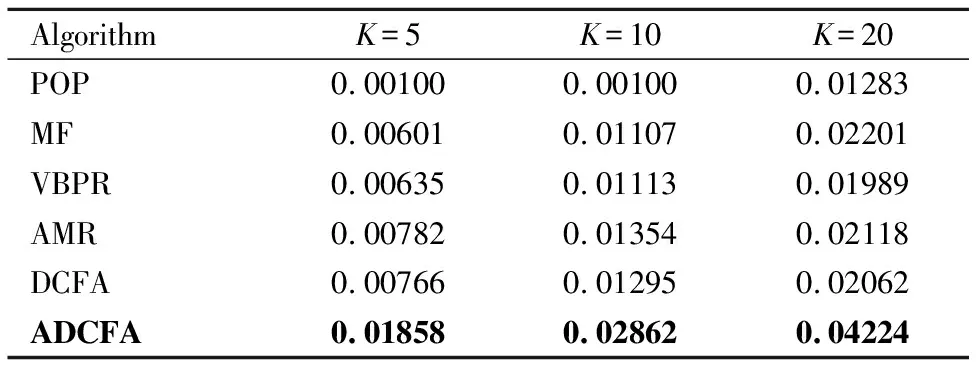
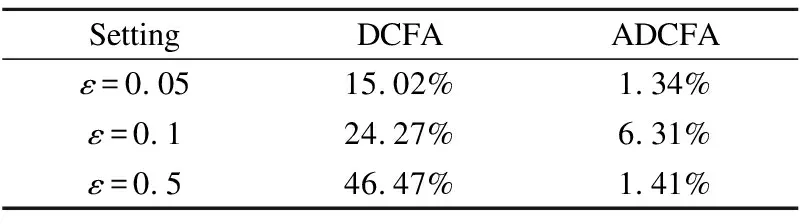
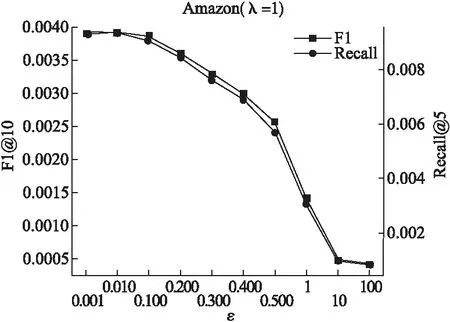
3.While参数未收敛&iter 4.iter+=1; 5.从训练集中随机选一实例(p,q,q′,r); 6.构建对抗性扰动; 7.更新模型参数; 8.end. 9.return Θ. 该算法的关键步骤是如何为一个实例(p,q,q′,r)构建对抗性扰动(步骤6)以及模型参数的更新(步骤7). 构建对抗性扰动的目标函数为: (14) 另外,如果最小化实例的目标函数,就能获得模型参数,使模型能够抵抗在该实例上被破坏的情况. 模型参数学习的目标函数为: (15) 实验选择亚马逊鞋子类公开数据集验证本文提出算法的性能.亚马逊鞋子类数据集含有用户的消费信息、产品信息等.实验中所用数据集的统计特性如表1所示. 表1 数据集统计信息 模型的美学特征是使用美学网络在美学视觉分析(AVA)数据集(1)https://www.dpchallenge.com(训练得到的.它包含超过250,000张审美评级为1至10的图像,66个描述图像语义的文本标签,以及14种摄影风格(互补色、双色调、高动态范围、图像纹理、白色光、长曝光、微距、动态模糊、负重像、三分规则、浅景深、轮廓、软焦点和消失点),且都进行了审美排序. 本文采用准确率P、召回率R和F1值F1来评价推荐算法的性能,其定义如下: (16) (17) (18) 为了验证本文提出推荐算法的有效性,选取如下的推荐算法作为对比方法. 1)POP:是一种非个性化排名的方法,按照产品的受欢迎程度来进行排名,通过训练数据中的交互次数来衡量. 2)MF-BPR:使用BPR优化排序,把用户和产品分别以嵌入矩阵的形式表现出来,并用其内积来评价用户对一个产品的偏好程度. 3)VBPR:在MF-BPR基础上加入了视觉信息的模型,对于那些受视觉信息影响较大的推荐任务如:服装推荐等VBPR有其优越性. 4)AMR:在VBPR模型基础上利用对抗性学习训练得到的新模型.该模型相比较于VBPR有更好的鲁棒性和推荐效果. 5)DCFA:将美学特征融入到一个基于张量分解的模型中,可以根据用户的审美个性化推荐产品. 从数据集中随机抽取其中的80%作为训练,10%作为验证,剩余10%作为测试,其中验证集用于调整超参数,测试集用于性能比较.为了公平起见,不同算法中的参数设置如下:在MF中λU=0.1,λV=0.001;在VBPR中λ1=0.1,λ2=0.001,λ3=0;在AMR中3个正则化系数同VBPR,λadv=5,ε=0.01;在DCFA中λ1=λ2=0.1,λU=λV=0.3,λT=0.5,λW=0.2,λM=λN=0.5;对于本文提出的方法,正则化系数同DCFA,λadv=5,ε=0.01.另外所有算法的学习率η=0.03,潜在特征向量维度d=64. 本文实验的运行环境为:Intel(R)Core(TM)i7-8700 CPU,NVIDIA GeForce RTX 2080 GPU,16GB内存,2018.3.2 x64 PyCharm. 实验1.不同模型间性能对比 选择K={5,10,20}的Top-K推荐结果作为实验数据,进行不同模型间的性能对比,使用F1和Recall两个指标进行衡量.实验结果如表2、表3所示. 表2 F1指标下Top-K推荐性能对比 从表2、表3中可以发现:个性化推荐方法性能都远远优于非个性化推荐的方法.MF-BPR是一种应用隐式反馈的个性化排序,其结果优于非个性化的POP排序方法是因为个性化排序会对产品进行建模,而POP则是直接根据流行度来进行推荐排名. 表3 Recall指标下Top-K推荐性能对比 综合两个衡量指标,DCFA在亚马逊鞋子这个数据集上的推荐效果略优于VBPR,说明美学因素对鞋子这类产品的推荐中起到一定的积极作用. ADCFA优于DCFA,AMR优于VBPR,说明加入了对抗性学习不仅能改善模型的鲁棒性也可以提高模型的推荐性能. 进一步进行横向比较,随着K的增加,模型的Recall呈上升趋势,即Top-20的推荐效果最好,这与Recall的计算公式有关,其公式的分母不变,分子随K的增大可能性增大.而F1指标综合了准确率和召回率,故过大和过小的K都会对其产生影响,综合上述模型的F1值,当K=10时推荐效果较好. 本文提出的ADCFA模型推荐效果显著优于上述所有对比模型,以此验证了本文算法的有效性.以F1指标而言,在K=5,10,20时ADCFA的Top-K推荐效果就DCFA分别提升了62.5%,76.9%,73.8%. 实验2.模型的鲁棒性对比 为了验证使用对抗性学习的效果,本文选用模型的鲁棒性来进行分析对比.首先,使用BPR优化训练DCFA直至其基本达到收敛,然后将收敛的DCFA参数用来初始化ADCFA并进行迭代训练至其收敛.实验结果如表4所示. 表4 不同ε情况下模型性能变化对比 该表不仅记录了DCFA和ADCFA模型在加入相同大小扰动后性能变化的幅度,也记录了它们在加入不同ε所带来的不同大小扰动下性能的变化.从该表中可知,当DCFA和ADCFA加入相同大小的扰动时,例如当ε=0.05时,DCFA性能下降的幅度明显大于ADCFA,相较于未加入扰动时的性能,DCFA性能下降了15.02%,而ADCFA性能只下降了1.34%.这表明了ADCFA模型想比较于基础模型DCFA更能抵御来自外界的恶意攻击,对于对抗性扰动的敏感性降低,鲁棒性增强. 从另一个方面看,随着ε的增大即扰动的增大,模型性能受影响程度也增大,但ADCFA性能受影响程度总是小于DCFA,这也表明了ADCFA的鲁棒性优于DCFA,对抗性学习确实能改善模型的鲁棒性. 实验3.超参数对模型的影响 为了分析超参数对ADCFA模型性能的影响,本文详细地讨论了各超参数下的实验结果.本文设定超参数ε的取值为0.001,0.01,0.1,0.2,0.3,0.4,0.5,1,10,100,超参数λadv的取值为0.001,0.01,0.1,1,5,10,50,100,1000,10000,100000.选用Recall和F1作为评价指标.从图 3和图 4可得出结论: 1)超参数ε控制着在对抗性学习中加入扰动的大小,其实验结果如图 3所示.随着ε的增加,模型性能指标总趋势下降,当ε=0.01时,模型性能达到最优;当ε取值在0.1~0.5的范围时,模型性能下降相对平缓;当ε>0.5时,模型性能下降明显;当ε超过100时性能曲线几乎降为0,这说明过大的扰动会严重破坏模型参数的学习过程. 图3 ε的影响 超参数λadv控制着对抗性扰动所产生损失函数在总损失函数中的影响力,其实验结果如图4所示.随着λadv的增加,模型性能的总趋势先增加后下降,当λadv=5时,模型性能达到最优;当λadv<5时,模型性能随着λadv的增大而增强;当λadv>5时,模型性能反而随着λadv的增大而下降,当λadv增大到100时,性能下降至最低.当λadv=1000时,模型性能总趋势又相对稳定,这说明当λadv足够大的时候,ADCFA 模型对于对抗性扰动的敏感性减弱. 图4 λ的影响 实验4.算法时间复杂度的分析比较 选取基线模型DCFA与本文的ADCFA进行算法时间复杂度的分析比较. 为更好地表示两种算法在训练时的时间复杂度,分别定义Of、Ob、Ou为前向传播、反向传播、更新模型参数所需的时间复杂度,另外还引入了Oadv表示扰动计算过程中的时间复杂度.根据DCFA和ADCFA的损失函数,本文可以得到它们的时间复杂度分别为2×Of+2×Ob+Ou、4×Of+4×Ob+2×Oadv+Ou.其中Of、Ob、Ou相较于Oadv有着较大的影响,故ADCFA的复杂度约为DCFA的两倍. 另外,还进行了将这两种算法在同一数据集训练同一周期的时间对比实验.在本文实验的运行环境下,DCFA约花费了6秒来运行一个周期,ADCFA则花费了约12秒.结果表明ADCFA训练所需时间约为DCFA的两倍,这也符合上述对这两种算法时间复杂度的分析比较. 本文主要针对美学因子作为视觉特征的DCFA模型展开研究,通过在美学因子特征参数处加入随机和对抗性两种扰动,验证了恶意攻击动态美学因子会降低模型鲁棒性的猜想.然后,通过在模型参数处添加对抗性扰动使其性能达到最差,并使用对抗性学习的方法来改善模型的鲁棒性.本文详细阐述了构建对抗性扰动的方法以及利用SGD方法设计了优化模型的算法,在亚马逊数据集上进行实验.与目前已知的其它推荐模型进行对比,结果表明改进模型有效提高了模型的推荐性能和鲁棒性. 后继研究工作将尝试在ADCFA模型中加入一些上下文特征进行推荐,如频谱特征、听觉特征等;另外还可以在本文方法的基础上研究其在显式反馈推荐中的效果.
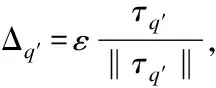
5 实验分析

5.1 实验设置
5.2 实验结果及分析

6 结 论
